Injection Spectra of Different Species of Cosmic Rays from AMS-02, ACECRIS and Voyager-1

Xu Pan and Qiang Yuan

1 Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210023, China; yuanq@pmo.ac.cn

2 School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, China

Abstract Precise measurements of energy spectra of different cosmic ray(CR)species have been obtained in recent years,by particularly the AMS-02 experiment on the International Space Station.It has been shown that apparent differences exist in different groups of the primary CRs.However,it is not straightforward to conclude that the source spectra of different particle groups are different since they will experience different propagation processes (e.g., energy losses and fragmentations)either.In this work,we study the injection spectra of different nuclear species using the measurements from Voyager-1 outside the solar system,and ACR-CRIS and AMS-02 on the top of atmosphere,in a physical framework of CR transportation.Two types of injection spectra are assumed, the broken power-law(BPL)form and the non-parametric spline interpolation form.The non-parametric form fits the data better than the BPL form,implying that potential structures beyond the constrained spectral shape of BPL may exist.For different nuclei the injection spectra are overall similar in shape but do show some differences among each other.For the non-parametric spectral form, the helium injection spectrum is the softest at low energies and the hardest at high energies.For both spectral shapes, the low-energy injection spectrum of neon is the hardest among all these species,and the carbon and oxygen spectra have more prominent bumps in 1–10 GV in the R dN dR 2 presentation.Such differences suggest the existence of differences in the sources or acceleration processes of various nuclei of CRs.

Key words: (ISM:) cosmic rays – acceleration of particles – astroparticle physics

1.Introduction

Although the exact origin of cosmic rays (CRs) is not clear yet, it is generally believed that CRs with energies below PeV originate from supernova remnants.Energetic CRs were accelerated by diffusive shocks and then injected into the interstellar space.Theoretically, the accelerated spectrum can be simply described by a power-law formdN dR∝R-n,with R being the particle rigidity and n being the index(Fermi 1949;Bell 1978,2014;Blandford&Ostriker 1978).Extension of the conventional diffusive shock acceleration mechanism with test particle assumption to consider the interaction between accelerated particles and the surrounding fluid results in nonlinear effects and deviation from the simple power-law spectrum (Malkov & Drury 2001; Bell 2004; Caprioli et al.2010).From the observational point of view, complicated spectral structures of CRs were also revealed by many measurements (Panov et al.2009; Ahn et al.2010; Adriani et al.2011, 2019, 2020; Aguilar et al.2015a, 2015b, 2017;Atkin et al.2018;An et al.2019;Alemanno et al.2021,2022).Particularly, apart from the breaks around a few GV, remarkable hardenings around hundreds of GV and subsequent softenings around 10 TV were shown by the data.The spectra also differ among different nuclei.The helium spectrum is found to be clearly harder than that of protons (Adriani et al.2011; Aguilar et al.2015a, 2015b).The AMS-02 measurements further showed that the high-energy spectra of neon(Ne),magnesium(Mg),and silicon(Si)are different from those of helium(He),carbon(C),and oxygen(O),and suggested that different types of primary sources exist (Aguilar et al.2020).These results may indicate that the origin and acceleration of CRs are more complicated.

It should be noted that after the acceleration,CR particles are injected into the interstellar space, and experience complex propagation processes.The energy losses and fragmentation cross sections of various nuclei differ from each other,making the propagated spectra become diverse even for the same injection spectra.Therefore, the apparent differences of the spectra are not directly reflecting the differences at injection.To properly address this issue needs a thorough consideration of the CR propagation (Yuan et al.2017; Boschini et al.2018, 2020a, 2020b; Derome et al.2019; Wu & Chen 2019;Yuan 2019; Korsmeier & Cuoco 2022; Niu 2022).

Here we investigate the source injection spectra of different primary nuclei including He, C, O, Ne, Mg, Si, and Fe,based mainly on the AMS-02 data (Aguilar et al.2017, 2020, 2021a, 2021b).At low energies the fluxes will be suppressed due to the solar modulation effect.We use the forcefield approximation to account for the solar modulation (Gleeson& Axford 1967).To break the degeneracy between the injection and the solar modulation effects,the measurements at low energies outside the solar system by Voyager-1 will also be included(Cummings et al.2016).We further use the ACE-CRIS3http://www.srl.caltech.edu/ACE/ASC/level2/lvl2DATA_CRIS.htmlmeasurements at the same time periods of the AMS-02 to better constrain the low-energy spectra.The GALPROP code is employed to calculate the propagation of CRs (Moskalenko &Strong 1998; Strong & Moskalenko 1998).The Markov Chain Monte Carlo (MCMC) method is used to do the fit (Liu et al.2012).

Compared with previous works along the line of studying the injection spectra of CRs (Yuan 2019; Korsmeier &Cuoco 2022; Niu 2022), this work differs in either more species of nuclei used (e.g., Ne, Mg,Si,Fe) or the low-energy ACE and Voyager data included which better constrain the wide-band spectral shape.

2.Cosmic Ray Injection and Propagation

Given more and more complicated structures of the CR spectra were revealed by recent precise measurements, it is expected that simple empirical functions may not be proper enough to describe the injection spectra of CRs in a wide energy range.In this work, we use a non-parametric interpolation (NPI) spectrum determined by a cubic spline interpolation method (Ghelfi et al.2016; Zhu et al.2018),which has more freedom to reveal multiple structures of the spectra.The interpolation is done in the log (R) – log(J)parameter space, where R=pc/Ze is the particle rigidity in unit of MV and J is the flux.Specifically,we set the following rigidity knots in the analysis:

where γ0, γ1, and γ2are spectral indices in different rigidity ranges, Rbr0and Rbr1are break rigidities.

Following the distribution of supernova remnants,the source distribution of CRs is parameterized as

where r⊙=8.5 kpc, zs=0.2 kpc, α=1.25, β=3.56 (Trotta et al.2011).

The propagation of nuclei in the Milky Way includes mainly the diffusion in the random magnetic field, the energy losses due to ionization and Coulomb collisions, the fragmentation due to inelastic collisions with the interstellar medium, and possible convective transportation and reacceleration (Ginzburg&Syrovatskii 1964;Strong et al.2007).The propagation can be described by a set of differential equations for all species of nuclei, which self-consistently predict the fluxes of both primary and secondary nuclei.The general propagation equations can not be solved analytically, and numerical solutions were developed and widely employed (Moskalenko& Strong 1998; Strong & Moskalenko 1998).

The propagation parameters we adopt are determined through fitting to the newest measurements of secondary and primary CRs (Yuan et al.2020).We work in the diffusionreacceleration framework, and the convection velocity is set to be 0.The main parameters include: the spatial diffusion coefficient Dxx=D0βη(R/4 GV)δ, with D0=7.69×1028cm2s−1, η=−0.05 which phenomenologically describes the possible resonant interactions of CRs with the magnetohydrodynamic (MHD) waves (Ptuskin et al.2006), δ=0.362,the Alfvénic velocity vA=33.76 km s−1which characterizes the reacceleration of particles during the propagation, and the half height of the propagation halo zh=6.27 kpc.

After entering the solar system, CRs would be further affected by the magnetic field carried by the solar wind, and experience flux suppression at low energies (below tens GV).This so-called solar modulation results in an anti-correlation of the low-energy CR fluxes with solar activities.Although more sophisticated modulation models were developed (e.g.,Potgieter 2013),the simple force-field approximation(Gleeson& Axford 1967) is employed in this work.Since the particles discussed here are all positively charged with mass-to-charge ratio A/Z ≈2, we expect that their relatively differences are less sensitive to the solar modulation model.

3.Analysis Method

In this work we focus on the primary CR nuclei with A/Z ≈2, including He, C, O, Ne, Mg, Si, and Fe.The proton spectrum which shows clear difference from that of He is not discussed(Zhang et al.2017).The CosRayMC code(Liu et al.2012) which combines the CR propagation and the MCMC sampler is used.According to the Bayes’theorem,the posterior probability of a model described by parameters θ can beobtained as

Table 1 The Parameters of BPL Form of Injection Spectra

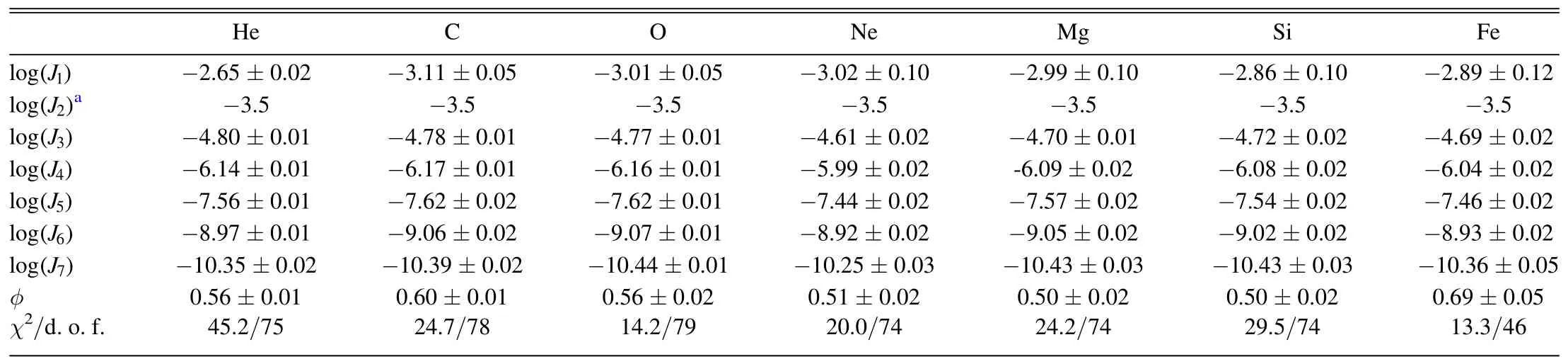
Table 2 The Parameters of NPI Form of Injection Spectra

where J(Ei;θ) is the model predicted flux, Jiand σiare the observational flux and error of the ith energy bin.

The AMS-02 and Voyager-1 data can be directly obtained from the publications (Cummings et al.2016; Aguilar et al.2021a).The total uncertainties used are the quadratic sum of the statistical ones and systematic ones.For the ACE-CRIS data, we extract them from the online data server.The systematic uncertainties of ACE-CRIS data include the geometry factor (2%), the scintillating optical fiber trajectory efficiency (2%), and the correction of spallation in the instrument (1%∼5% depending on the charge and energy bin) (George et al.2009).For He nuclei, no ACE-CRIS data are available.For Fe nuclei, the ACE-CRIS data are not included in the likelihood calculation due to the possible excess compared with the AMS-02 data (see the discussion in Boschini et al.2021).

4.Results

The best-fit parameters and the 1σ uncertainties for the BPL and NPI injection spectra are presented in Tables 1 and 2.For all species,the NPI form shows smaller reduced χ2values compared with those of the BPL form.Figure 1 displays the injection spectra of various nuclei(the 1σ bands)obtained from the fitting.The top panels are for the injection spectra normalized at 10 GV, and the bottom panels display the spectra which are grouped into four groups, He, C–O, Ne–Mg–Si, and Fe, respectively.These injection spectra show a general similarity among each other.Specifically, the injection spectra for all nuclei experience softenings around several GV rigidities and hardenings around a few hundred GV.For the BPL form,our results of C,O,Ne,and Mg are consistent with those given in Niu (2022), despite the methodologies are different.The relative spectral shapes among different nuclei are different for the BPL and NPI forms.Since the NPI form introduces less constraints on the injection spectra,and the fittings are much better than the BPL form,we take the results from the NPI fitting as benchmark.The helium spectrum is the softest at low energies and the hardest at high energies.The Ne spectrum is the hardest in the low-energy range among all species.For C and O,their injection spectra show prominent bumps in the 1–10 GV range compared with other nuclei.The Fe spectrum is similar to that of Si at low energies, but is slightly harder above 10 GV.

Figure 1.The injection spectra of different nuclei.In the top panels we normalize all spectra at 10 GV, and in the bottom panels they are shown for four different groups.The left panels are for the BPL form, and the right panels are for the NPI form.

Figure 2.The one-dimensional probability density distributions of the solar modulation potentials, for the BPL form (left) and NPI form (right).

Thanks to the observations by Voyager-1 outside the solar system and the low-energy fluxes by ACE-CRIS, the degeneracy between the injection spectrum and the solar modulation can be effectively broken.Figure 2 shows the probability distributions of the solar modulation potentials φ for different nuclei.For both the BPL and NPI forms, Fe has the largest φ value.The remaining nuclei exhibit similar modulation potentials within ∼2σ uncertainties.The difference of modulation potentials between Fe and the other nuclei may be due to the low-energy structures of the Fe spectrum as revealed by combining the ACE-CRIS and AMS-02 data (see the discussion below).

Figure 3.Comparison of the best-fit results of the spectra with the measurements(Cummings et al.2016;Aguilar et al.2021a).In each panel the higher line is the LIS and the lower one is the TOA spectrum.The residuals are depicted in the lower sub-panel,defined as χ=(data −model)/error(stars are for the BPL form and circles are for the NPI form).

Figure 3 shows the comparisons between the best-fit spectra and the measurements.The higher curve in each panel represents the local interstellar spectrum (LIS) before the solar modulation,and the lower one shows the spectrum at the top of atmosphere(TOA)of the Earth.Good consistency between the fitting results and the data can be seen.We also show that the ACE-CRIS measurement for the fluxes of Fe nuclei cannot connect smoothly with the AMS-02 data, as already being pointed out in Boschini et al.(2021).The combined AMS-02 and ACE-CRIS data may indicate a bump structure at ∼2 GV,which may be due to a past supernova explosion in the Local Bubble (Boschini et al.2021).

5.Conclusion and Discussion

New measurements of the energy spectra of CRs with presentlevel precision enable us to investigate crucially the acceleration and propagation processes of particles.The measured spectra contain mixed effects of the acceleration and propagation, and thus cannot be directly used to infer the injection spectra of different CR particles.In this work, we thus derive the source injection spectra of a series of primary nuclei under the framework of a physical propagation model.Our results show that,even these nuclei have similar A/Z ≈2, their injection spectra show diverse behaviors.As a test, we assume identical injection spectra for all these nuclei using the NPI form, and find a reduced chi-squared value of χ2/d.o.f.=9424.3/586.If we choose two injection spectra, one is applied to He, C, and O nuclei, and the other is applied to Ne, Mg, and Si nuclei, we obtain χ2/d.o.f.=650.3/275 for the fitting to He, C, and O, and χ2/d.o.f.=223.5/265 for the fitting to Ne, Mg, and Si.The fitting to C and O gives χ2/d.o.f=71.2/165, indicating that the injection spectrum of C and O should be different from that of He.When we add Fe to Ne–Mg–Si group, we obtain χ2/d.o.f.=672.0/319.The injection spectrum of Fe appears to be similar to those of Mg and Si at low energies,but is harder at high energies.The combined fitting of Fe and He–C–O gives χ2/d.o.f.=1164.8/339.These tests show that we can perhaps classify the injection spectra into four groups,He,C–O,Ne–Mg–Si, and Fe as shown in Figure 1.Assuming the same injection spectra for different groups result in poor fittings to the data,indicating the intrinsic difference of their injection spectra.

The diversity of the derived injection spectra may be related with the acceleration processes.Various acceleration models were proposed to explain the spectral differences of protons and helium nuclei.For example, it was proposed that the reverse shock acceleration of different supernova shocks (e.g.,Type I where hydrogen is absent,and Type II where hydrogen is abundant)could explain the harder spectrum of helium nuclei(Ptuskin et al.2013).Ohira & Ioka (2011) proposed that the acceleration in chemically enriched regions with outwarddecreasing abundance could naturally result in different spectra of different species.Those models may be extended to account for the differences of injection spectra of heavy nuclei as found in this work.In addition, models including different ionization histories of nuclei (Casse & Goret 1978) and condensation of different elements into grains (Ellison et al.1997) could also explain the diversity of the inferred injection spectra.

Note that we have assumed a single source population in derive the injection spectra.The results may reflect the fact that there are multiple source components of CRs.For example, it has been proposed that a nearby source with element abundance different from that of the average background sources may result in different spectral shapes of various nuclei(Yuan et al.2021).

Finally, we assume a spatially uniform propagation in this work.However, a number of new observations may suggest a spatially dependent propagation model of CRs (Tomassetti 2012; Guo & Yuan 2018; Liu et al.2018; Zhao et al.2021).Due to the differences of the energy loss rates and fragmentation cross sections of different nuclei, they experience different propagation lengths in the Milky Way.In the spatially dependent propagation model,such an effect results in additional spectral differences on the results based on homogeneous propagation assumption.Whether or not the observed spectral differences can be reproduced in a realistic spatially dependent propagation model needs future studies.

Acknowledgment s

We acknowledge the use of the ACE-CRIS data provided by the ACE Science Center.This work is supported by the National Key Research and Development Program of China(No.2021YFA0718404), the National Natural Science Foundation of China(No.12220101003)and the Project for Young Scientists in Basic Research of Chinese Academy of Sciences(No.YSBR-061).