基于几何相位的太赫兹编码超表面反射器研制与测试*

姜在超 宫正 钟芸襄 崔彬2) 邹斌2)† 杨玉平2)‡

1) (中央民族大学理学院,北京 100081)

2) (光子系统工程软件教育部工程研究中心,北京 100081)

1 引言

对电磁波的偏振态进行有效操控可以实现偏振器、光束聚焦、涡旋光束等众多电磁应用[1,2].传统的电磁偏振控制技术主要基于法拉第效应和双折射晶体[3,4],但这些方法面临的主要问题是调制范围有限、体积庞大且不利于集成.近年来,一种新兴的二维人工亚波长电磁结构——超表面(metasurfaces),因其在操纵电磁(EM)波方面的巨大潜力、多功能性、低损耗和易于在芯片上制造等优点而备受关注[5,6].它可以通过等效的电磁表面阻抗和突变的相位不连续性对电磁波进行多自由度、有效操控,如异常反射/折射[7-9]、吸收[10,11]、隐形[12,13]和偏振转换[14-16]等,超表面的研究和发展为电磁波的振幅、相位、偏振态以及传播模式的调控和波束赋形提供了一种新的技术路线[17-20].

在微波和太赫兹(THz)波段,Cui等[21]在2014年首次提出了编码超表面的概念,用于控制电磁波的传播;即具有0和π相位差的超表面单元分别表示为二进制编码粒子0和1,利用编码超表面可以实现对微波的有效调节.为了更自由地控制电磁波,数字编码超表面的概念已经扩展到更高阶的编码方式,如2-bit,3-bit编码等[22-28].类比于微波波段的编码超表面[29,30],基于数字编码超表面的THz波束调控与赋形技术也相继被提出.Qi等[31]设计了一种双开口劈裂环结构的超宽带偏振转换编码超表面,数值模拟和理论计算结果表明,该超表面在2.04—5.33 THz波段内可以将线偏振波转换为交叉偏振波,相对带宽达到了89%,且极化转换率(PCR)超过了90%.Zheng等[32]设计了一种全硅编码超表面,在0.50—2.50 THz范围内对入射THz波具有直接传输和随机散射的双重功能,通过实验验证,设计的超表面还能够分别产生涡旋光束的叠加态和贝塞尔涡旋光束.目前,基于数字编码理论,人们通过设计不同结构和尺寸参数的编码单元构成特定编码序列的超表面,初步实现了对电磁波的各种操控.但是,以往的研究通常都是基于表面等离子体的谐振机理,大多数超表面的有效带宽和相位覆盖范围由单元结构和尺寸参数决定,为了获得满足要求的单元结构,通常需要进行大量的参数扫描优化;且一旦结构加工完成,其性能往往固定不变,大大限制了其功能和效率.

为了实现更加简单高效的调控,将编码超表面与Pancharatnam-Berry (P-B)几何相位理论进行结合,得到P-B相位编码超表面.与以往通过设计多种结构或改变特定尺寸参数来控制电磁波的编码超表面设计不同,P-B编码超表面是通过旋转单元的几何图案来实现360°准连续的相位变化,对入射波的调控更加灵活.Tan等[33]将半导体InSb与P-B相位元素相结合,研制出了一种磁控可调谐的旋致P-B超表面,在1.02—1.70 THz的工作频率范围内,能够控制两种圆偏振(LCP和RCP)态的转换和实现36.6°—83.5°波束角度的偏转;不但在正入射情况下实现大角度偏折,且提供了一种获得左、右旋圆偏振光的方法.该超表面可用于离轴反射系统,有效地避免反射光被光学元件或感测器遮蔽的情况.Zhao等[34]提出了一种三层C型单元结构的编码超表面,并且将数字信号处理系统中的傅里叶卷积理论引入到P-B编码超表面中获得了新的不同编码序列,能够灵活地控制太赫兹波实现任意散射角的偏转,在操控太赫兹波和实现雷达散射截面(RCS)缩减方面具有重要应用.RCS的减小能够有效实现电磁隐身,可广泛应用于飞行器、探测器及军事领域的雷达隐身.然而,目前相关的报道多为数值模拟结果.

针对编码超表面反射器设计中面临反射率、工作频段、覆盖相位互相约束和测试等难题,在不改变单元的结构和尺寸的情况下,设计了一种反“S”形状的超表面结构单元;结合P-B相位理论设计编码超表面,通过旋转结构单元的角度来控制反射THz波的相位实现2π的相位全覆盖,并采用不同的编码粒子设计了几种功能型太赫兹反射器,实现了对反射太赫兹波的有效操控.此外,采用正入射和变角度的THz时域光谱仪分别对各个编码子单元结构阵列的反射相位和2-bit超表面的角度偏折现象进行测试;对比理论数值、模拟结果和实验结果,分析理论数值和实验数值之间存在偏差的原因,对满足实际需求的超表面逆向设计具有一定的借鉴意义.

2 理论与实验方法

2.1 P-B相位理论

P-B相位,又称几何相位,由Pancharatnam和Berry提出的理论相融合而产生,以反射情况为例,其基本原理为: 当一束圆偏振(CP)波入射到一个各向异性的亚波长结构上时,反射波的交叉极化分量会携带一个与该结构相对中心旋转的角度θ相关的相位延迟Φ=2mθ.m=-1时为左旋圆偏振(LCP)波入射,m=1时为右旋圆偏振(RCP)波入射.基于此原理,可以通过调整同一单元结构的旋转角度来使其相位发生变化.若把一个超表面单元从0°旋转180°,则经此单元反射的波相位变化能满足0—2π的全覆盖,为波束控制提供了更多可能.

2.2 广义Snell反射定律

2011年,哈佛大学Capasso首次在两种介质界面处引入了突变相位,从一维角度出发,基于费马原理进行异常折射和反射的推导,提出了广义的Snell定律[35].在斜入射情况下,以θi角入射到超表面上,在界面一定位移dx范围内产生相位突变dφ,然后以θr角反射出来,可得

其中ni为入射介质的折射率,θi和θr分别为入射角和反射角,dφ/dx为相位梯度.即在界面上存在相位突变(dφ/dx≠ 0)时,反射的角度与相位梯度的大小相关;反之,当dφ/dx=0时,则回归到传统的Snell反射定律.若入射介质为空气,ni=1;假设一个周期编码序列的物理长度为Γ,发生了2π的相位差,则(1)式可以改写为

进一步,在垂直入射情况下,得

编码超表面通常由N×N个编码元素阵列组成,每个元素由M×M个编码粒子阵列组成.因此,可以通过改变相应的编码序列(即晶格常数Г),以操控相同频率下的波束扫描.此外,类似于传统的Snell反射定律中存在全反射临界角,广义Snell反射定律同样有类似的现象.当sinθr=1时,根据(1)式可得

当入射角大于这一数值时,异常反射光束便会转化成表面波的形式而消失.

2.3 实验原理

分别采用正入射和变角度的反射式太赫兹时域光谱(THz-TDS)系统对编码单元和编码超表面进行测试,如图1所示.其中,正入射的THz-TDS系统由实验室自主搭建,其装置原理及仪器详见参考文献[36];变角度的THz-TDS系统是青源峰达太赫兹有限公司研发的QT-TO100太赫兹三位层析成像系统,入射角度固定在30°,反射角度在20°—60°连续可调;两个系统都为8f系统,且均采用天线产生和探测太赫兹波,泵浦光和探测光均为水平方向线偏振.

图1 反射式太赫兹时域光谱仪的结构示意图 (a) 正入射;(b) 变角度Fig.1.Schematic diagram of THz-TDS systems in reflection mode: (a) Normal incidence;(b) variable angle.

在测试过程中,首先在样品架上放置金属反射镜,此时接收的反射波作为入射THz光场信号(即);再在样品架上放置超表面反射器,经过超表面反射器反射的THz波作为反射信号(即),将入射信号与反射信号分别进行傅里叶变换,即可得到频域和.超表面反射器的振幅反射率r(ω)定义为入射与反射THz波的振幅比:

式中,Er(ω)为反射THz波的频域振幅谱,E0(ω)为入射THz波的频域振幅谱.

超表面反射器的反射相位φr定义为入射波与超表面反射波的相位差,可由下式计算得到

式中,φr为超表面单元的相位差,为反射THz光场,为入射THz光场.

3 单元结构设计与仿真

本文设计了由编码粒子组成的超表面,以实现对太赫兹波的操控.这些编码粒子由基本编码单元通过特定参数形成,如图2(a)所示.编码粒子由顶层金属图案、中间介质层和底层金属薄膜构成,其中中间介质层的材料为聚酰亚胺.单元的周期为Px=Py=P=60 μm;聚酰亚胺介电基板介质层的厚度h=30 μm,相对介电常数ε=3.5,损耗角正切tanδ=0.01;金属图案和底层金属薄膜的材料选用金,导电率σ=4.56×107S/m,厚度为0.2 μm.通过仿真优化得到编码粒子的尺寸:L=16 μm,R1=10 μm,R2=5 μm.该结构的上下半圆形开口环具有谐振电路的特性,其中间的金属棒具有偶极子共振的特性,其倾斜的结构又引入了几何相位,从而在作用带宽和相位调制中具有广范围的相位调制梯度.

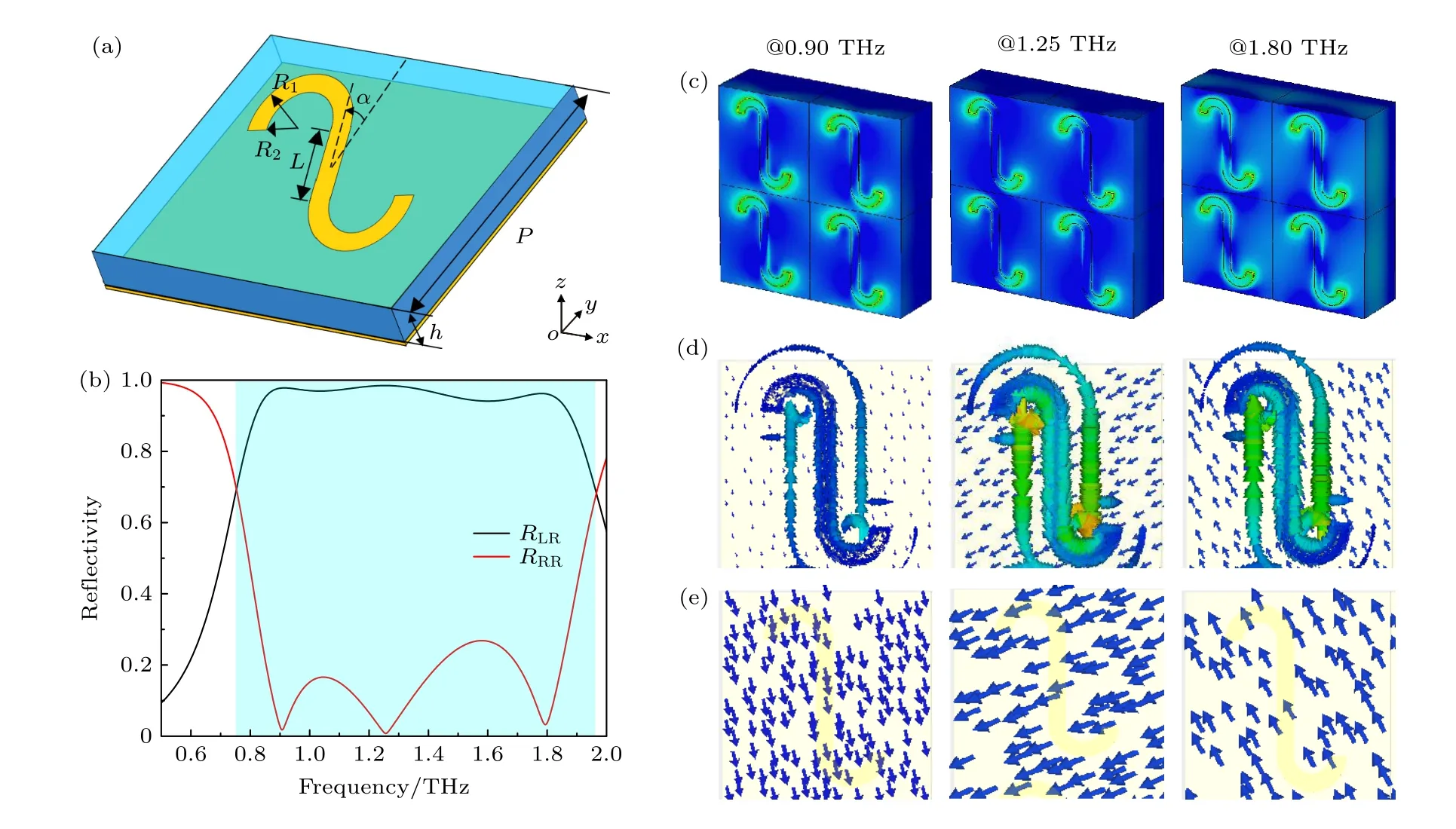
图2 (a) 编码粒子的结构示意图;(b) 圆偏振波正入射下单元的同偏振和交叉偏振的振幅反射率;三个谐振频率处结构单元的表面电场(c)、表面电流(d)和背面电流(e)的分布图Fig.2.(a) Structure of coded particle;(b) co-polarization and cross-polarization amplitude reflectivities of the unit under normal incidence of circularly polarized waves;distribution diagrams of the front surface electric field (c),front surface current (d),and rear surface current (e) of the structural unit at three resonant frequencies.

为了分析该编码粒子的偏振特性,通过有限元方法(FEM)来计算CP波正入射下的同偏振反射和交叉偏振反射.图2(b)给出了0.40—2.00 THz频率范围内的模拟结果,其中RLL(RRR)和RRL(RLR)分别代表LCP和RCP波的同偏振和交叉偏振波的振幅反射率.由图2(b)可知,在0.80—1.90 THz范围内,反射波主要为交叉偏振波,编码粒子的交叉偏振振幅反射率大于80% (蓝色区域).此外,编码粒子在该频率范围内有3个谐振频率分别为0.90,1.25和1.80 THz,三个频率点处的电场分布、表面电流和背面电流分布如图2(c)—(e)所示.由图2(c)—(e)可以看出,在0.90 THz处金属图案的表面电流方向和背面电流方向相反,形成了磁谐振;在1.25 THz处同时存在电谐振和磁谐振;在1.80 THz处金属图案的表面电流方向和背面电流方向相同,形成了电谐振.因此,这种结构单元存在多种电磁谐振模式,3个谐振点的叠加使得该单元结构具有宽频带高效率的工作特性.

在CP波正常入射的情况下,可以通过简单地控制结构单元的旋转角度来控制相位,即CP波的反射相位差Δφ与结构单元旋转角α密切相关,可以表示为Δφ=±2α,“+”表示入射波为RCP波,“-”表示入射波是LCP波,α是顶部金属图案的不同旋转角度.图3分别给出了旋转角度α为 0°,22.5°,45°,67.5°,90°,112.5°,135°和157.5°时的单元结构,以及在LCP波和RCP波正入射下具有不同旋转角度的交叉偏振反射的模拟幅度和相位.8个单元在整个带宽中的反射幅度都在0.8以上;同时,当旋转角α以22.5°步长增加时,反射相位在整个频率范围内以45°梯度增加.8个编码粒子与1-bit,2-bit和3-bit编码P-B相位超表面数字元素的关系如图3(a)所示,定义当编码粒子的Δφ为0°和±180°时分别对应“0”和“1”数字状态,作为1-bit编码超表面的数字元素.对于2-bit编码超表面,Δφ为 0°,90°,180°,270°四种反射相位差,对应的基本数字元素分别为“00”,“01”,“10”和“11”.类似地,对于3-bit编码超表面,采用8个固定反射相位差为45°的编码粒子来模拟“000”,“001”,“010”,“011”,“100”,“101”,“110”和“111”的数字位.基于这种推导方法,可以将编码超表面扩展到更高位,使编码序列更加多样化,实现更广泛的应用.

图3 不同旋转角α对应的(a)八个超表面编码粒子、(b)交叉偏振反射率和(c)反射相位Fig.3.(a) Eight coded particles and the corresponding cross-polarized amplitude reflection (b) and phase (c) at different rotation angles α.

4 编码超表面的设计与仿真

4.1 1-bit 编码超表面

将1-bit编码粒子“0”和“1”在水平方向按[01010101···]的排布顺序,竖直方向采用相同的编码方式,排布成1-bit编码超表面时.当线偏振(LP)波垂直入射到1-bit编码超表面时,入射THz波在1.5 THz处的远场散射波束沿垂直于超表面的方向反射,且反射波束只有一个主瓣,如图4所示.根据(1)式,在1.5 THz频率处,λ=200 μm,Γ=2P=120 μm,sinθr＞ 1,相位突变引起的反射光束偏折大于90°并沿超表面界面消失;图4中的单波束反射满足正常Snell反射定律,且反射效率高达80%以上.因此,在设计2-bit和3-bit编码超表面中,需要改变相应的编码序列(即晶格常数Г),以操控相同频率下的波束扫描.

图4 1.5 THz 线偏振波法向入射下1-bit编码超表面的远场散射图 (a) 3D远场散射图;(b) 2D远场散射图Fig.4.Far-field scattering patterns of 1-bit encoded metasurface under normal incidence of LP waves at 1.5 THz: (a) 3D far-field scattering pattern;(b) 2D far-field scattering map.

4.2 2-bit编码超表面

将2-bit编码粒子“00”,“01”,“10”,“11”分别按每四个一组构成新编码序列的单元,在水平方向按[00000000 01010101 10101010 11111111 ···]的排布顺序,竖直方向采用相同的编码方式,排布2-bit反射超表面阵列.当线偏振(LP)波垂直入射到2-bit编码超表面时,反射THz波在1.5 THz处的远场散射分布如图5(a)和图5(b)所示.可以看出,法向入射的LP波分别被反射到对于法线对称的两个方向,分别为LCP波和RCP波.因此,该2-bit超表面不但可以分别获得左、右旋圆偏振光,还可以使左、右旋圆偏振光分离,且角度相等、方向相反;其中法线右侧的是RCP,法线左侧的是LCP,单独展示RCP和LCP入射下的结果如图5(c)和图5(d)所示.根据(3)式,在1.5 THz频率处,λ=200 μm,Γ=16,P=960 μm,对应反射角度的理论值为12°,与模拟结果吻合.但是,在LP入射时,由于左、右旋圆偏振光各分走一部分能量,两个光束的反射效率均低于50%;而在单独的左旋或右旋圆偏振(LCP或RCP)入射时,偏折反射光束的反射率则高于80%.

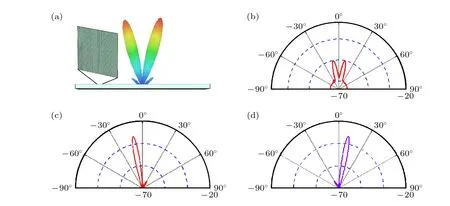
图5 1.5 THz线偏振(LP)波法向入射下2-bit编码超表面的远场散射图,其中(a) 3D远场散射,(b) 2D远场散射;1.5 THz圆偏振(CP)波法向入射下2-bit编码超表面2D远场散射图,其中(c)右旋圆偏振(RCP),(d)左旋圆偏振(LCP)Fig.5.Far-field scattering patterns of 2-bit encoded metasurface under normal incidence of LP waves at 1.5 THz: (a) 3D far-field scattering pattern;(b) 2D far-field scattering map.2D far-field scattering patterns of 2-bit encoded metasurface under normal incidence of CP waves at 1.5 THz: (c) RCP;(d) LCP.

4.3 3-bit编码超表面

将3-bit编码粒子“000”,“001”,“010”,“011”,“100”,“101”,“110”,“111”分别按每四个一组构成新编码序列的单元,在水平方向按[000 ···001 ···010 ···011 ···100 ···101 ···110 ···111 ···]的排布顺序,竖直方向采用相同的编码方式,排布3-bit反射超表面阵列.图6(a)—(h)显示了当LP波垂直入射时该编码超表面在1.50—1.80 THz时的散射模式.为了定量地比较设计的3-bit编码超表面和相同尺寸的裸金属板的散射特性,在相同的频率下模拟了该编码超表面和相同尺寸的裸金属板在xoz平面上的2D散射模式,如图6(e)—(l)所示.从图6可以看出,对于相同尺寸的裸金属板,后向散射峰明显.然而,对于3-bit编码超表面来说,后向散射受到了抑制,并且在1.50和1.80 THz处存在大量旁瓣.

图6 LP波法向入射下3-bit编码超表面和相同尺寸的裸金属板的远场散射图 (a) 1.50 THz处编码超表面的3D远场散射图;(b) 1.60 THz处编码超表面的3D远场散射图;(c) 1.70 THz处编码超表面的3D远场散射图;(d) 1.80 THz处编码超表面的3D远场散射图;(e) 1.50 THz处编码超表面的2D远场散射图;(f) 1.60 THz处编码超表面的2D远场散射图;(g) 1.70 THz处编码超表面的2D远场散射图;(h) 1.80 THz处编码超表面的2D远场散射图;(i) 1.50 THz处裸金属板的2D远场散射图;(j) 1.60 THz处裸金属板的2D远场散射图;(k) 1.70 THz处裸金属板的2D远场散射图;(l) 1.80 THz处裸金属板的2D远场散射图Fig.6.Far-field scattering patterns of a 3-bit encoded metasurface and a bare metal plate under normal incidence of LP waves: 3D far-field scattering pattern of the encoded metasurface at 1.50 (a),1.60 (b),1.70 (c) and 1.8 THz (d);2D far-field scattering pattern of the encoded metasurface at 1.50 (e),1.60 (f),1.70 (g) and 1.80 THz (h);2D far-field scattering pattern of bare metal plate at 1.50 (i),1.60 (j),1.70 (k) and 1.80 THz (l).

5 测试与分析

5.1 编码单元

为了验证反S型编码超表面阵列的反射特性,首先利用正入射的反射式太赫兹时域光谱系统(如图1(a)所示)对微纳加工制作的超表面单元结构进行反射实验测试,得到图7(a)和图7(b)所示的时域和频域信号.图7(c)是不同旋转角度α的单元反射率测试图,插图为制备出的旋转角度α为0°的编码单元阵列显微图.在0.50—1.40 THz范围内结构单元的反射率在80%以上,整体反射率变化不大;在1.40—1.80 THz范围内,编码单元的反射率出现较大的波动.

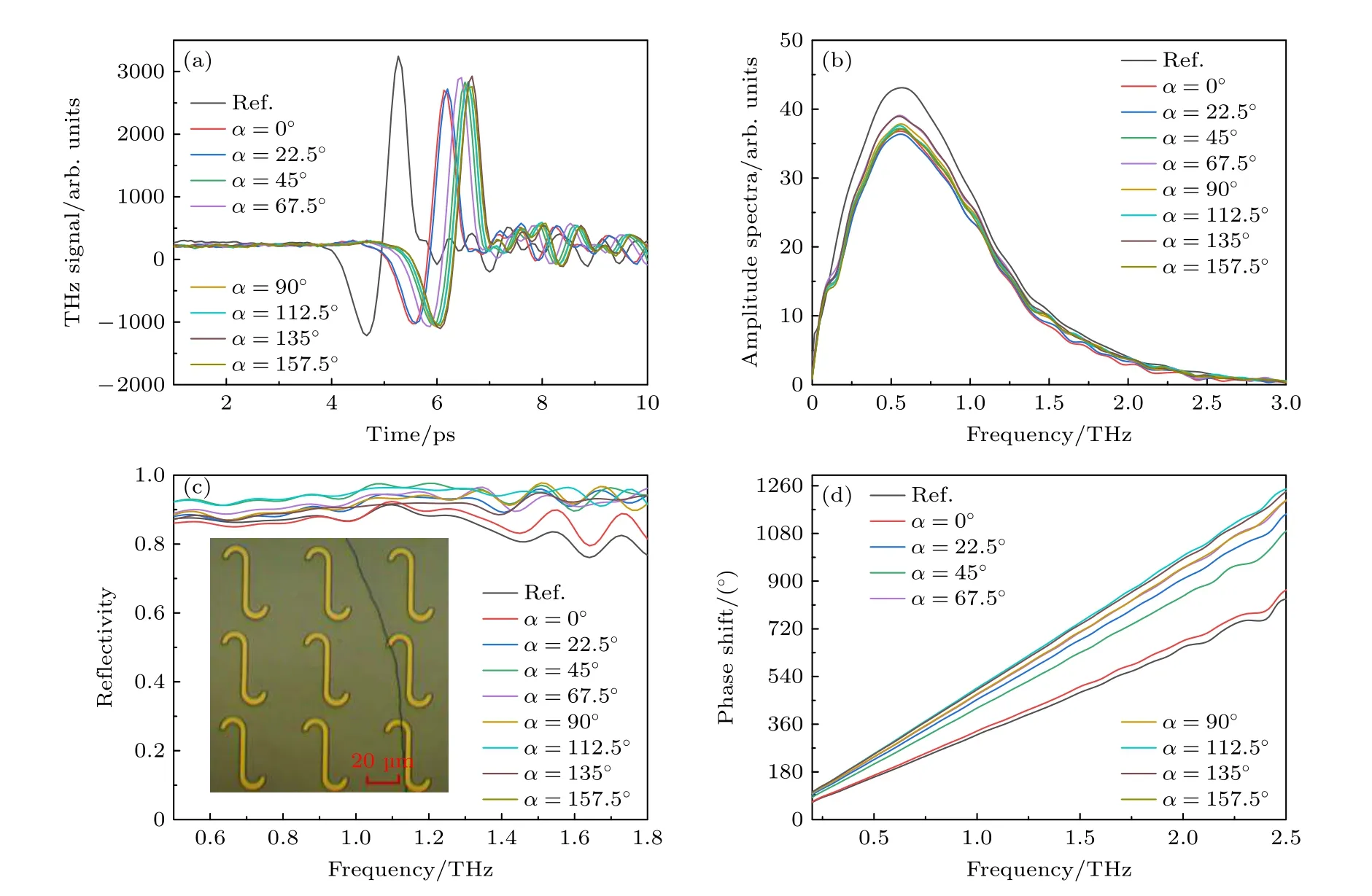
图7 各个编码单元的反射特性测试结果 (a) 时域波形图;(b) FFT频谱图;(c) 反射率;(d) 反射相移Fig.7.Reflection characteristics of each encoding unit: (a) Time-domain waveforms;(b) FFT spectra;(c) reflectivity;(d) phase shift.

图7(d)表明单元之间相位差范围不同.可以看出,在0.8—1.9 THz范围内,8个子单元结构的相位调制范围为142°—339°;且相位覆盖范围随频率的增加而增大,其中,1.00,1.50 和1.80 THz的反射波在一个周期Γ中相位覆盖分别为176°,263°和315°.此外,还存在相位变化平行性较差,相位差梯度不均匀等问题,这些因素可能会对实际设计的超表面器件的性能造成影响.

5.2 2-bit编码超表面

利用变角度的反射式太赫兹时域光谱系统(如图1(b)所示)对微纳加工制作的2-bit编码超表面进行反射实验测试,其中入射角度保持在30°,反射角度的扫描范围为20°—60°,角度间隔为1°.采集到的时域信号随反射角度的增加先增大后减小,但时域信号的最大值位置基本保持不变.为了便于观察,选取部分时域波形,并将主峰位置分别移动0.2 ps,画于图8(a)中.取时域波形的最大值(Ep),绘制其随反射角度的变化,如图8(b)所示.可以看出,在30°—45°之间,存在两个较宽的峰重叠;30°—35°之间为传统Snell反射峰(P0),40°—45°之间为相位突变引起的异常反射峰(P1).由于两峰难以分开,采用多峰拟合(蓝线),拟合出P0(红线)和P1(绿线)两个峰,分别对应的角度为31.5°和40.6°.其中,P0峰的强度和面积占主体地位,角度31.5°可能是由于样品放置时角度发生微小倾斜造成的;而P1峰的强度和面积明显低于P0峰,说明相位突变引起的异常反射效率较低.实验测量时,入射太赫兹波为线偏振,而图5中模拟的反射波束为分离的左旋或右旋圆偏振;此外,8f光路中样品处的THz光斑仅为2—3 mm,不能完整覆盖我们设计的超表面.因此,实验观测的关于相位梯度引起的反射波束P1偏转现象非常弱,远低于常规的Snell反射P0.

图8 不同反射角度下2-bit编码超表面的反射特性测试结果 (a)时域波形图;(b)时域信号最大值Ep;(c) 1.00,1.50和1.80 THz的振幅反射率.Fig.8.Reflection characteristics of 2-bit coded metasurface under different reflection angles: (a) Time-domain waveforms;(b) the maximum value Ep of the time-domain signal;(c) the frequency components at 1.00,1.50 and 1.80 THz.

类似地,绘制1.00,1.50和1.80 THz三个频率分量的振幅反射率随反射角度的变化,并采用双峰拟合,其中P0峰固定在31.5°,观察不同频率分量P1峰的反射角度变化,如图8(c)所示.发现异常反射波在1.00,1.50和1.80 THz处的反射角度拟合值(P1)分别为40°,41°和46°,而根据(1)式计算得到的理论数值分别为54°,45°和42.对比分析理论数值和实验数值之间存在的偏差,发现频率越低,偏移量越大.根据图7(d)实验测试结果可以看出,各个编码子单元结构引起的相位调制范围均低于2π;且频率越低,相位调制范围越小;这是引起理论数值和实验数值之间存在偏差的主要原因.根据图7(d)中的实验结果,1.00,1.50和1.80 THz的反射波在一个周期Γ 中实际产生的相位跳变范围分别为0.49×2π,0.73×2π和0.875×2π,代入(1)式,则反射波在1.00,1.50和1.80 THz处的反射角度理论值分别为40.1°,40.7°和40.6°,与图8(b)和图8(c)中拟合的P1峰对应的角度基本吻合.

在基于相位梯度的超表面设计中,实际加工和测试中引起的相位偏差问题不可避免.造成偏差的主要原因有以下几点: 1) 实物加工工艺存在结构尺寸误差;2) 实物加工材料参数误差、PI介质层的厚度、介质损耗也会对结果产生影响;3) 各个编码子单元结构的相位突变是在周期性边界条件下模拟得到的,而组成超表面的各个子单元之间存在的强耦合作用使得相邻子单元的反射相位发生串扰,与仿真结果产生差异;4) TDS测试系统一般具有偏振敏感特性(入射波为LP波),而模拟产生的反射角偏折波束是分离的部分圆偏振(LCP或RCP) THz波,测试效率低于模拟值;5) 反射式TDS系统的测试过程中,样品的复位精度和放置角度均需满足严格条件,否则将严重影响相位提取精度.虽然本文的实验结果与模拟结果有一定偏差,仍对对满足实际需求的超表面逆向设计有一定的借鉴意义.今后可以考虑将两种或以上的相位梯度表面融合,比如在改变单元结构的尺寸和形状形成突变相位的基础上添加几何相位,不仅弥补结构变化导致相位覆盖范围小的缺点,还补充了几何相位的可调性.后续的实验测试研究仍需不断深入并改进,比如采用圆偏振太赫兹波的反射测试装置[37],利用4f光路的平行太赫兹光束照射样品[38]等;且为了避免大量试错的成本,将引入机器学习的方法更加高效地设计具有优良反射特性的超表面器件.

6 结论

本文基于编码电磁超表面和几何相位的基本原理,综合利用数值仿真、微纳加工技术和太赫兹时域光谱系统对超表面阵列和单元进行仿真、分析、加工及测试.对比测试结果、模拟结果和理论数值,可以看出,1-bit和2-bit超表面的正常Snell反射效率均高于80%,但由于相位梯度引起的异常反射效率较低;此外,异常反射波束的偏折角度也跟模拟数值有一定的偏差,利用实验中获得的相位覆盖范围数值,获得了与理论数值一致的结果,验证了广义Snell反射定律的有效性,为今后设计满足实际需求的可调控超表面反射器提供了实验依据.