基于ISSA-BPNN 算法的配电线路绝缘跳线夹过热感知方法

王南极，吴田，江全才，徐勇，梁加凯，蔡豪

（1. 三峡大学电气与新能源学院，湖北 宜昌 443002；2. 湖北省输电线路工程技术研究中心，湖北 宜昌 443002；3. 国网金华供电公司，浙江 金华 321000）

0 引言

在配网不停电作业［1］中通常需要转移负荷来确保检修过程中不损失负荷，以保证用户持续供电，绝缘跳线是一种常用的带负荷更换发热线夹、柱上隔离开关的通流工具。若跳线夹过流或其他不良条件下工作时间较长，会导致跳线夹过热，甚至绝缘手柄熔融、绝缘性能降低，将影响配电线路的正常运行和作业人员的人身安全，因此分析绝缘跳线夹的电-热问题，增强工具对过热状态的感知能力，对确保带电作业人员和设备安全具有重要意义。

目前，线夹因为环境、老化、振动和腐蚀等因素容易出现接触不良，导致发热、过热甚至金具烧蚀，现阶段一些学者通过有限元法对不同类型线夹的温升进行了大量研究。例如，通过多物理场对J型线夹进行电-热-力耦合仿真计算，结果表明不同条件下影响线夹与导线接触面的电流［2］及温度分布规律［3-4］。目前配网不停电作业的规模越来越大，设备种类多，作业设备状态的感知应用不足且智能化水平低。随着人工智能、物联网和大数据等技术的快速发展，电网中将会产生大量数据，为基于智能算法对设备故障诊断及温度预测提供数据基础，目前遗传算法（genetic algorithm，GA）、支持向量机（support vector machine，SVM）、BP 神经网络（back propagation neural network，BPNN）及群体智能优化等多种算法在电力设备状态智能诊断中得到了大量的应用［5-8］。相对于传统算法存在收敛速度慢及容易出现过拟合等不足，群体智能优化算法具有鲁棒性强、收敛速度快，常被采用优化BPNN、GA、SVM 等传统智能算法存在的问题［9］。2020 年以来群体算法中的麻雀搜索算法引起了研究人员的关注，其基于麻雀觅食和躲避掠食者行为而提出的群体优化算法［10］。然而麻雀搜索算法在迭代后期容易出现局部极值的问题，对此多位学者提出利用混沌映射法、自适应权重因子、反向学习策略及柯西突变等方法改进麻雀搜索算法提高其收敛速度及精度［11-14］。通过上述多种方法对麻雀搜索算法进行改进并与BP 神经网络相融合提高优化算法全局寻优和搜索能力，如文献［15］利用其对气动光学成像偏移进行预测及文献［16］对变压器故障诊断的研究。综上所述，采用改进麻雀搜索算法优化BPNN 可以提高收敛速度、预测精度。为了提升配网不停电作业绝缘跳线夹工作的安全性和智能化水平，本文基于ISSA-BPNN 算法对配电线路绝缘跳线夹过热感知预测开展研究。

本文以2756/SJ15303 型跳线夹为研究对象，基于多物理场耦合方法建立三维几何模型与电-热多物理场耦合模型，并通过试验验证仿真模型的有效性，分析线夹在光照、风速、环境温度及负荷电流因素下绝缘跳线夹温升特性，基于ISSA-BPNN 算法对线夹温度进行预测，并与SSA-BPNN、PSOBPNN、GA-BPNN 及BP 神经网络算法预测模型进行对比分析，为绝缘跳线夹在夏季高温、高负荷等条件下工作时的状态检测提供参考。

1 基于电-热-流体的多物理耦合的绝缘跳线夹温升模型

1.1 多物理场的控制方程及边界条件

1.1.1 电磁热耦合方程

绝缘跳线夹工作时负荷电流流过导线、引流线以及绝缘跳线夹，线夹各部分产生焦耳热而导致其温升。绝缘跳线夹各部分的发热可由电磁场计算获取损耗，然后通过传热理论计算发热与散热之间平衡，获取绝缘跳线夹各部分温度分布。

根据麦克斯韦方程组，并引入矢量磁位A，在外加激励电源为电流时，其矢量控制方程［17］为：

式中：μ为材料磁导率，H/m；A为矢量磁位；σ为电导率，S/m；Js为外施电流密度，A/m2；ω为角频率，rad/s。

在求解电磁场问题时，边界面具有电流密度J，及n×H=J，然后使用矢量磁位A进行描述，表达式为：

式中：n为边界上单位法向矢量；H为磁场强度。

电磁场与温度场之间存在耦合，可以通过热传导控制求解温度分布。因此首先求解方程中热源，而热源由电磁场中计算电磁损耗密度决定，而绝缘跳线夹金属导体部分电磁损耗与电导率相关，又因电导率随着温度变化，所以绝缘跳线夹的电磁场与温度场之间存在一定的耦合。

当导线施加工频电流时，通过式（1）计算矢量磁位A后进而求得绝缘跳线夹各部分的电磁损耗密度为：

式中：J为电流密度；Qe为单位体积电磁损耗。

绝缘跳线夹金属导体部分的电导率与温度之间满足以下关系。

式中：σ为当前温度下电导率；σ20为20 ℃下电导率；α为温度系数；T为导体当前温度。

通过电磁场计算绝缘跳线夹金属导体部分电磁损耗作为温度场热源，并由温度场模型中的固体与固体之间相互传热来获取线夹各部分温度分布，其热传导控制方程［18］如下。

式中：ρ为密度；Cp为恒压热容；k为导热系数；T为温度；υ为速度；Q为发热量。

1.1.2 流体传热控制方程

分析绝缘跳线夹在不同风速条件下绝缘跳线夹各部分温度分布，因此考虑空气流体在空气域边界入口设置一定速度，由于流体的粘性作用，所以空气域内流体需满足动量守恒方程，空气域中流体动量守恒方程为：

式中：ρT为气体密度，kg/m3；υ为流体速度矢量，m/s；η0为气体动力粘度，Pa·s；τ为流体粘度系数；F为流体所受到的重力；p为流体压力，N。

根据流体传热边界条件设计空气域，并设置开放边界；为模拟风速，假定外部空气处于强制对流情况，设置风速流入入口与出口边界，空气流速根据需要设置。

1.1.3 辐射传热控制方程

因绝缘跳线夹在夏季带电作业工作时会受到不同时刻光照作用，进而影响线夹各部分温升，对此考虑到线夹温度与外部环境之间热辐射传递，辐射传热方程为［19］：

式中：Qf为辐射换热量；ε为表面发射系数；Sf为辐射接触面积；δ为常数，数值为5.67×10-8W/（m2·K2）；T0为导体温度；T1为外部温度。

计算绝缘跳线夹温升时需考虑太阳辐射的作用，线夹表面辐射热量Qs表达式［19］为：

式中：Qfs为太阳辐射热量；β为外部表面吸收率；F为水平投影面积。太阳辐射传热的条件为：表面辐射率为0.9，环境温度为293.15 K。

1.2 模型建立及简化

本文以2756/SJ15303 型跳线夹为研究对象，在配电线路不停电作业时通过绝缘跳线夹将电流进行转移，其实物图及简化模型如图1 所示，图中1 为导线、2 为绝缘跳线夹上夹具、3 为绝缘盖、4 为绝缘跳线夹下夹具、5 为绝缘手柄、6 为引流线。引流线截面为91.6 mm2，半径为5.4 mm；线夹长为350 mm，宽为91 mm，高为52 mm；导线型号为LGJ300/40，其外径为23.94 mm，用铝柱体进行等效。线夹及导线模型各部分的仿真参数［2］如表1 所示。本文对绝缘跳线夹温度场进行计算，设定接触面的施加压力为0.5 MPa［2］；初始环境温度为293.15 K。

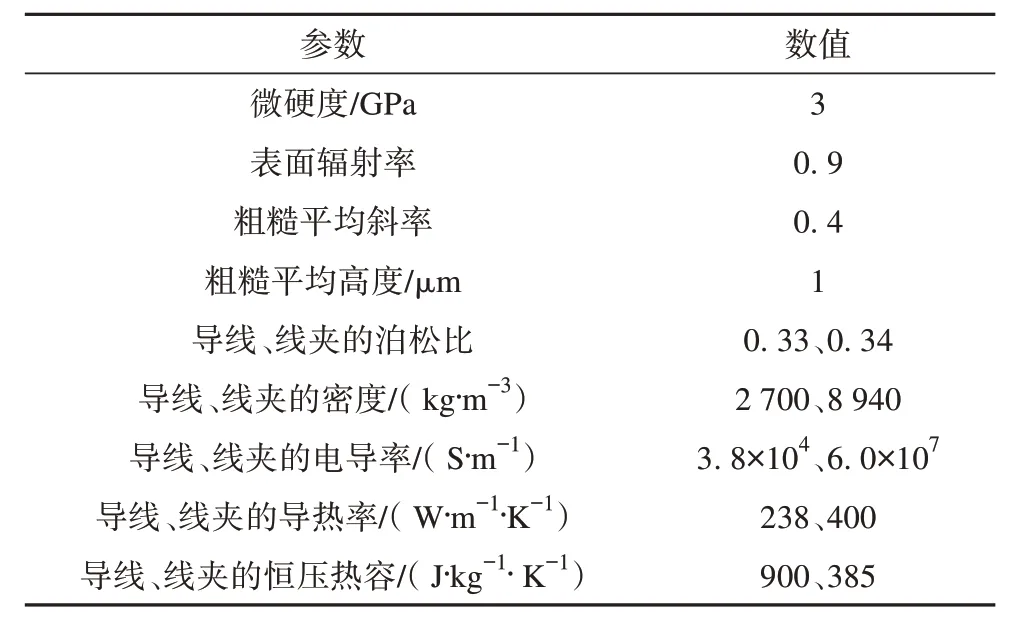
表1 仿真模型参数表Tab. 1 Simulation model parameter

图1 实物图及仿真模型Fig.1 Physical drawings and simulation models

1.3 试验验证

为了提供线夹温度感知模型的训练数据样本，通过多物理场仿真计算获取绝缘跳线夹在电流、光照、环境、风速等条件下的各部分温度分布，但由于光照、风速、环境温度等试验条件难以控制，因此通过仿真获取相应工况下线夹各部分温度分布。为了验证线夹与导线的电-热耦合场计算模型的有效性，搭建试验平台见图2，试验设备包括大电流发生器、电流互感器、钳形电流表、绝缘跳线夹、热电偶及采集设备。给线夹施加不同电流负荷，当线夹温度维持恒定时，记录不同电流水平下线夹温度及环境相关数据，试验与仿真结果如表2 所示。通过表2 可知绝缘跳线夹在不同负荷下试验温度与仿真时相比平均误差在4%左右，因此本文建立绝缘跳线线夹的电-热耦合模型有效性。

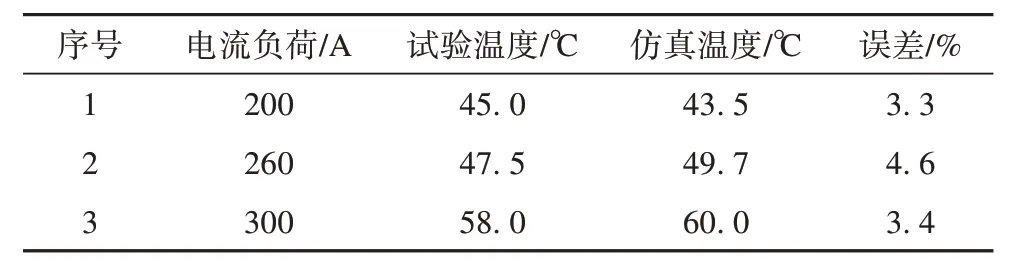
表2 实验数据与仿真数据对比Tab. 2 Comparison between experimental data and simulation data

图2 试验平台Fig. 2 Test platform

1.4 线夹温升影响因素设置

绝缘跳线夹是10 kV 配电线路不停电作业常用的带负荷检修工具，因此研究线夹温升影响因素具有重要意义。影响线夹温升的因素有光照强度、环境温度风速及旁路电流负荷，在计算中各因素参数设置如下。

1） 电流负荷。由绝缘跳线夹型号可知最大持续电流为300 A，因此本文将设置导线负荷电流分别为50、160、225、300 A。

2） 环境温度。本文将环境温度从常温293.15 K开始升至313.15 K共5个温度水平，增量为5 K。

3） 光照强度。根据我国部分地区夏季典型的不同时刻光照强度变化趋势［20］，本文设置光照强度分别为600、800、1 000、1 200 W/m2。

4）风速。根据我国地区平均风速变化为1~4 m/s［21］，本文设置风速为1~4 m/s。

2 基于ISSA-BPNN 神经网络线夹温度预测模型

本文基于电-热耦合方法获取不停电作业绝缘跳线夹在不同工况下的温度数据，因其工作负荷电流、光照、环境温度及风速等影响因素使得负荷和温度变化趋势表现为复杂的非线性关系，根据智能算法在非线性预测控制上能够提高预测控制对各种因素的不确定性的自适应能力，增强了预测模型的精确度。因此，本文采用群体智能优化算法（改进麻雀搜索算法）对传统算法（BP 神经网络）进行优化来提高绝缘跳线夹温度预测精度和适应性。

2.1 麻雀搜索算法(SSA)模型

SSA 算法是一种受麻雀觅食和躲避掠食者行为而提出的群体优化算法，由Xue［10］在2020 年引入，与灰狼算法（GWO）、粒子群算法（PSO）和引力搜索算法（GSA）相比，该算法在寻优过程中能够快速收敛于最优值附近，具有较高的稳定性，适用于全局最优搜索。

在SSA 寻优过程，当遇到危险时麻雀种群会做出反捕食行为，在其算法迭代过程中发现个体位置更新如下。

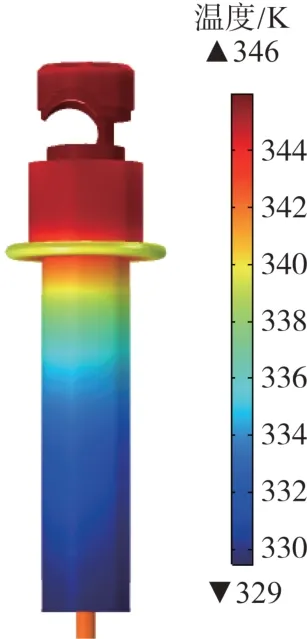
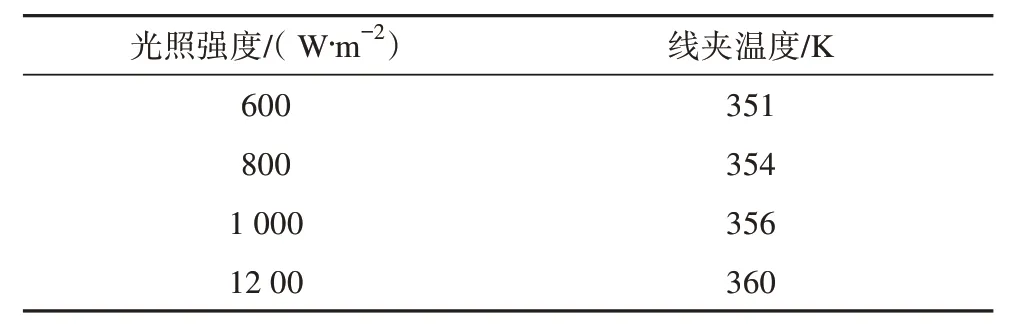
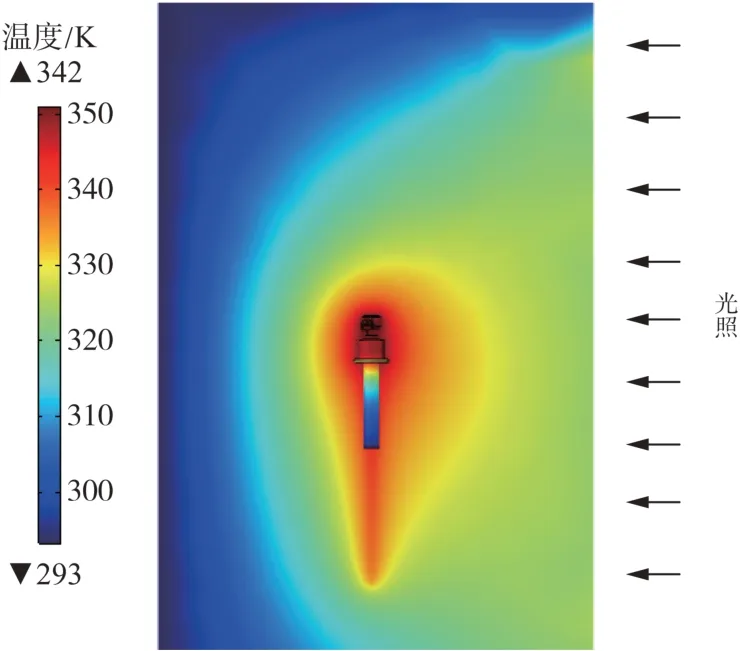
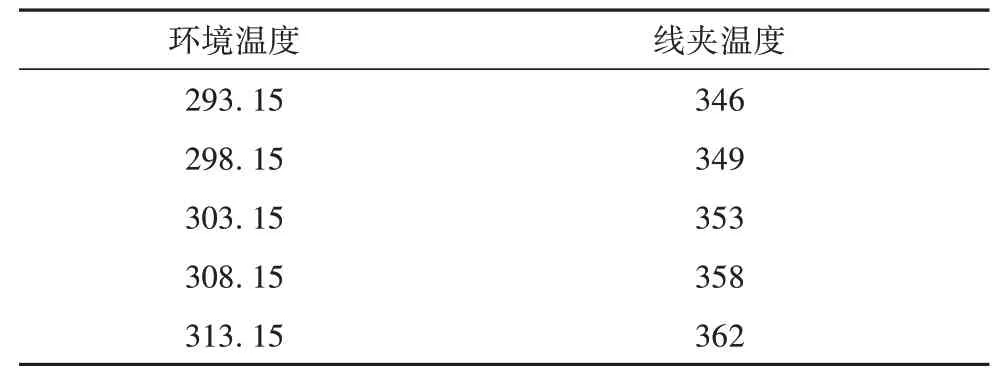
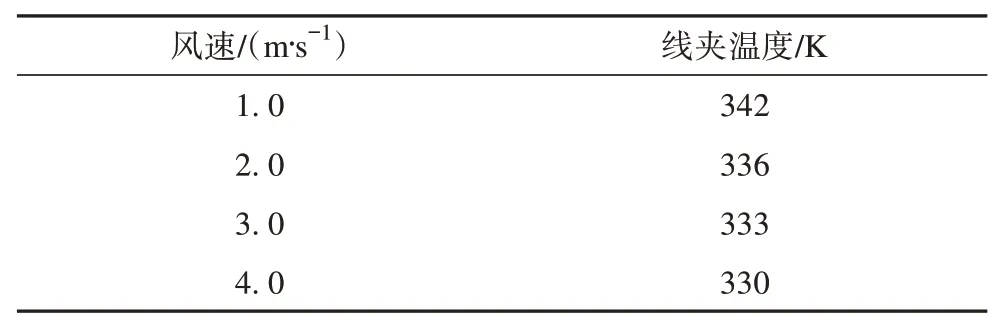
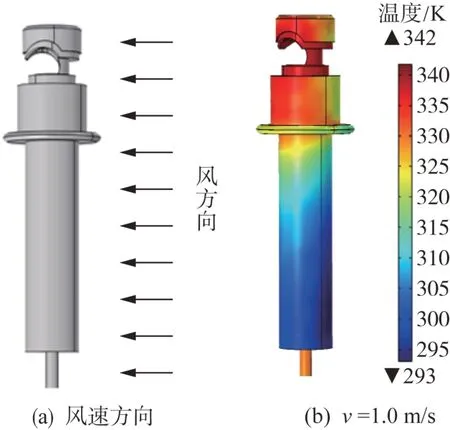
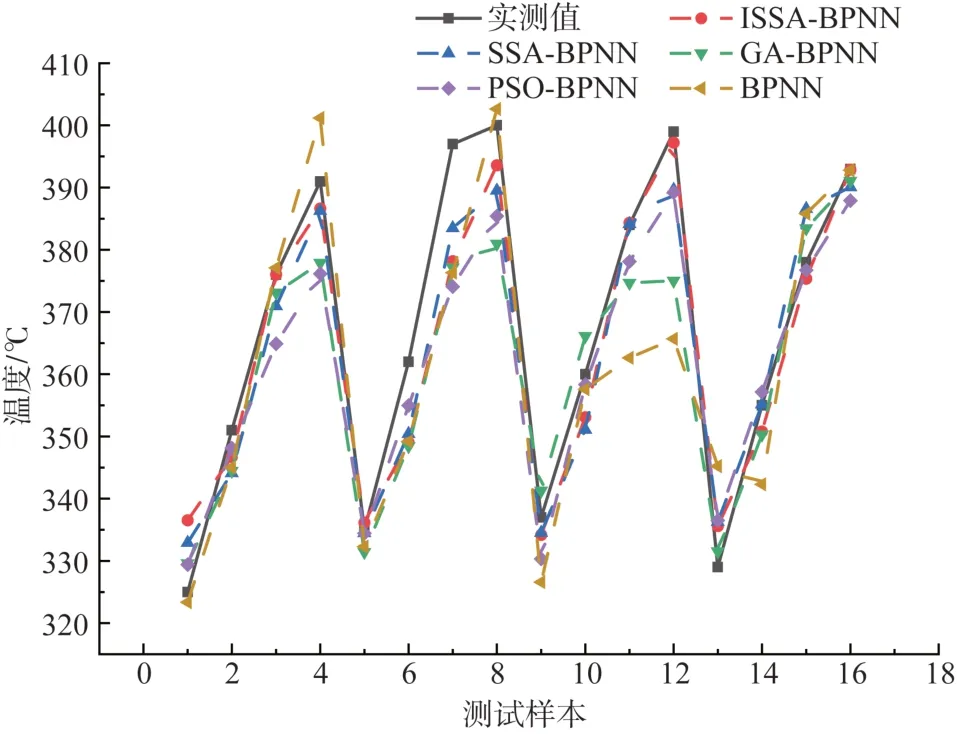
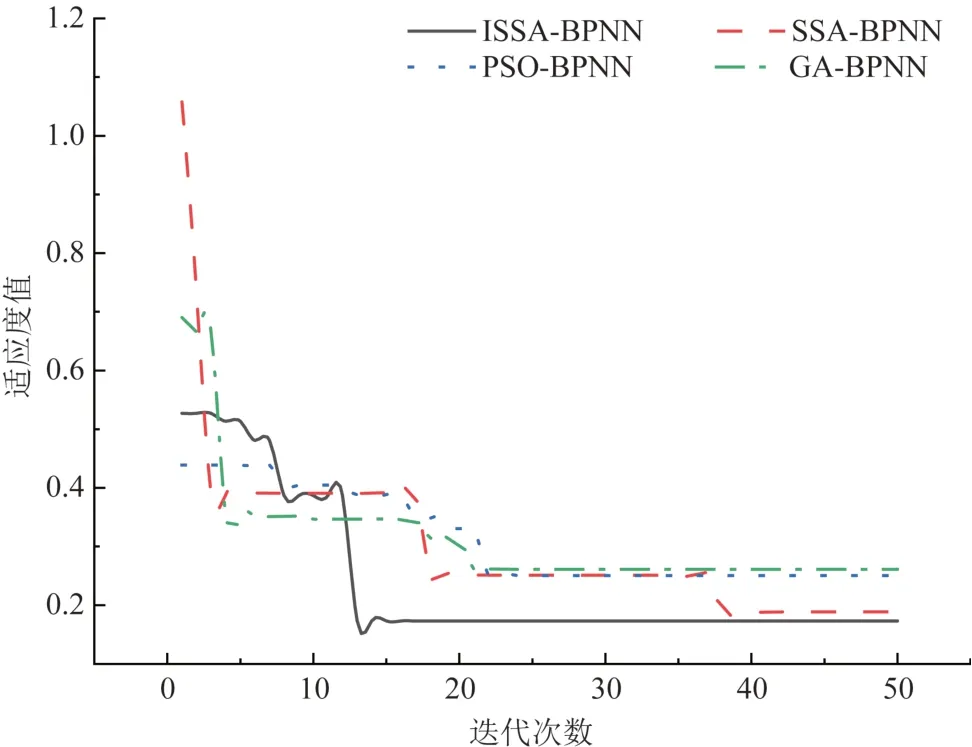
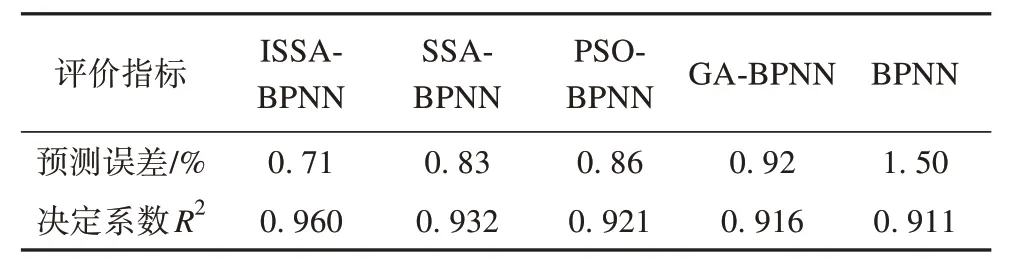
式中：t为当前迭代次数；Q为服从标准正态分布随机数；Xt i，j为第i个麻雀在j维的位置；L为每个元素都为1的矩阵；γ为0~1的随机数；Nmaxiter为最大迭代次数；R2为预警值范围为0~1，ST为安全阈值范围为0.5~1；当R2≥ST表示种群中一部分麻雀发现捕食者，并警告种群中的其他麻雀迅速飞到其他安全的觅食地点；当R2

在觅食过程中，部分加入者总是会对发现者有所警觉，一旦它们察觉发现者找到了更好的食物，它们就会立即离开当前的位置去争夺这些食物。此外，如果加入者在比赛中获胜，就可以立即获得发现者的食物。更新后的加入者的位置描述如下。

式中：n为种群规模数量；A为1×d 的矩阵，其中矩阵中的每个元素被随机赋值为1 或-1；且A+=AT（AAT）-1；为第t+1 次迭代发现者最优位置；为当前全局最差位置［23］。

当i>n/2 时，表示适应度差的第i个加入者没有得到食物，因此它必须到其他区域寻找更多的能量，目前一部分麻雀负责警戒，此时这部分麻雀最新位置更新为：

式中：为当前全局最优位置；K为一个随机数，范围为-1~1；c为步长控制参数，为服从于方差为1、均值为0 的正态分布的随机数；fi、fw、fg分别为当前麻雀个体的适应度、最差适应度和最佳适应度；θ为一个很小的常数。

2.2 改进的麻雀搜索算法(ISSA)模型

反向学习策略［16］（opposition-based learning）应用于种群进化过程中，其针对每一个种群个体的位置信息并作出反向的位置。本文通过一般动态反向学习策略对SSA 寻优迭代过程中，由目前种群个体信息生成反向个体信息，并对目前个体适应度与反向个体适应度进行比较，选择较优的个体作为下一代，从而提高SSA 种群多样性及收敛速度，进而提高其全局搜索能力。

为对应的反向个体信息。

式中：为第i个麻雀在j维的反向位置；、分别为最小值、最大值；k1、k2为取值范围在0~1之间的随机数。

由于SSA 在进行全局寻优时不能准确确定最优解的位置，在迭代后期容易出现局部极值的问题降低收敛速度与精度。因此，利用反向学习策略［16］麻雀种群中发现者的位置进行修改，能够选出较优的个体位置，提高了麻雀种群的多样性及SSA 的全局搜索能力与收敛速度。

SSA 引入动态反向学习后发现者位置更正如下。

1） 计算种群中所有发现者位置更新后的信息；

2） 根据式（13）计算出麻雀种群个体的反向个体；

3） 计算个体的适应度值，并选出较优的个体和反向个体作为新的种群个体进入下一次迭代。

2.3 ISSA优化BP神经网络(ISSA-BPNN)模型

通过BP 神经网络算法对基于电-热耦合方法在不同工况下绝缘跳线夹温度进行预测，但其预测模型在迭代过程中收敛速度较慢而且较容易出现过拟合等不足，因此本文采用上述ISSA 对BP 神经网络模型进行优化，目的在于提升其对绝缘跳线夹在不同工况下温度的预测精度及在迭代过程中的收敛速度。

ISSA 优化BPNN 算法的温度预测流程分为以下步骤［24］。流程图如图3所示，优化过程如下。

1） 通过计算麻雀适应度值确定其个体极值和全局最优极值；

2） 用式（10）—（12）更新麻雀的位置，得到麻雀适应度的更新值。

3） 根据新的适应度值反复更新麻雀的个体极值和全局极值。

4） 若不满足期望条件，则返回步骤2）。

5） 当适应度值达到期望值或者迭代次数达到设置的最大次数时，ISSA 结束，此时，根据得到的最优值设置BPNN的权值和阈值。

2.4 模型评价指标

本文采用ISSA-BPNN 算法对绝缘跳线夹温度进行预测，选取线夹的负荷电流、环境温度及光照强度作为模型的输入变量，以线夹的温度作为模型的输出变量。

为了评价本文提出的改进算法模型的准确性，本文选取均方值（f）作为适应度函数［25］和决定系数（R2）作为模型的评价指标，其中决定系数R2能够显示算法模型的准确程度，R2的数值越接近1，表示模型的准确程度越高，均方值表示实测值与预测值的偏差，偏差越小，预测精度越高，公式如下。

式中：i为测试样本数；f为适应度函数；R2为决定系数N为训练集的总个数；Ti为实测值；T′i为预测值；-Ti为实测值的平均值。

3 结果分析与讨论

3.1 负荷电流

导线的载流量大小也是线夹温升的重要因素，在导线载流量为300 A 且无风速载荷及光照条件下，其中环境温度为293.15 K，线夹各部分温度分布如图4 所示，线夹温度最高集中在与导线接触段，最高温升为53 K。当导线在不同载流量下线夹温升随负荷电流变化曲线如图5 所示，由图5 可知线夹整体温升与导线载流量呈平方关系。

图4 绝缘跳线夹温度分布Fig. 4 Temperature distribution of insulation jumper

图5 温升随载流量变化规律Fig. 5 Variation law of temperature rise with current carrying capacity

3.2 光照强度

由于绝缘线夹长时间暴露于大气环境中，故光照强度势必会影响其温升过程。因此，根据本文对光照强度与绝缘线夹之间的计算可知光照强度的大小对绝缘跳线夹的温升具有显著的影响，即绝缘跳线夹温升随着光照强度的增加而增加，当光照强度每升高200 W/m2，线夹温度平均上升3 K，当光照强度为1 200 W/m2时，线夹温度比无光照强度下温度增加了14 K。由此可见，当绝缘跳线夹在夏季高温、高负载率和高日照条件使用绝缘跳线夹时，线夹温度将更容易出现过热而影响其正常使用，如图6和表3所示。

表3 线夹随光照强度变化时温度Tab. 3 Temperatures of wire clip change with light intensities

图6 光照强度为600 W/m2时绝缘跳线夹温度分布Fig. 6 Temperature distribution of insulation jump clamp at 600 W/m2

3.3 环境温度

绝缘线夹与环境之间的温差会对线夹与空气间的对流换热和热辐射过程产生影响。本文计算线夹在导线载流量为300 A 时线夹温度在不同环境温度下变化情况，如表4 所示，由表4 可知在环境温度从293.15 K（20 ℃）到313.15 K，环境温度升高20 K，绝缘跳线夹温度随着环境温度的升高，且环境温度每升高1 K线夹温度均升高1 K。

表4 线夹随环境温度变化时温度Tab. 4 Temperatures of the cable clip change with the ambient temperaturesK

3.4 风速

根据我国地区平均风速变化为1~4 m/s［21］，风夹角为0 度时散热效果最好，因而计算时考虑1~4 m/s 风速对线夹温升的影响，计算结果如表5 所示，图7 为风速为1 m/s 时线夹温度分布图。结果表明，绝缘跳线夹的温升随着风速的增加明显的下降，但是温升的下降幅度较小；在风速为1~2 m/s，线夹的温升下降较快，当风速每增加1 m/s，绝缘跳线夹温升降低3 K 左右。同时，与图4 相比图7 线夹温度比无风速条件下降低4 K。

表5 线夹随着风速变化时温度Tab. 5 Temperatures of wire clip change with wind speeds

图7 绝缘跳线夹温度分布Fig. 7 Temperature distribution of insulation jumper

3.5 预测结果与分析

为了验证本文提出ISSA-BPNN 模型对线夹温度预测准确性，将与BPNN、SSA-BPNN、PSOBPNN 及GA-BPNN 模型进行比较，其中这4 种算法模型的参数设置与ISSA-BPNN算法模型一致。

图8为ISSA-BPNN与SSA-BPNN、PSO-BPNN、GA-BPNN 及BPNN 模型的预测值与实测值的结果对比，通过各模型结果对比显示ISSA-BPNN 模型对线夹温度的预测值更加接近实测值，预测误差相比其余上述4种算法较小。

图8 各优化算法的预测值与实际值对比Fig. 8 Comparison of predicted values and actual values of all the optimization algorithms

各模型适应度曲线如图9 所示，从图9 可以看出GA-BPNN 模型在迭代21 次后趋于稳定，PSOBPNN 模型适应度值与GA-BPNN 模型相近，但该模型收敛速度慢，对于SSA-BPNN 模型的适应度值比PSO-BPNN 与GA-BPNN 模型的低，但其迭代38次后趋于稳定收敛速度较慢，然而ISSA-BPNN 模型与上述3 种优化算法相比其适应度曲线在迭代13次后趋于稳定，表明ISSA-BPNN 算法模型比其他3种算法收敛速度更快，而且ISSA-BPNN 模型适应度值远远小于上述3种优化算法。

图9 各优化算法预测适应度Fig. 9 Prediction fitnesses of all the optimization algorithms

由表6可知，ISSA-BPNN 算法模型线夹温度预测误差为0.71%，模型的决定系数为0.960，相比于 SSA-BPNN［26］、 PSO-BPNN、 GA-BPNN 及BPNN 模型的决定系数R2更加接近于1，预测误差较小，显然ISSA-BPNN 模型对线夹温度预测优于其他4种算法模型［27］。

表6 各模型评价指标Tab. 6 Evaluation indexes of all the models

4 结论

本文通过电-热多物理场耦合方法对不同条件下绝缘跳线夹进行温度场计算，并利用ISSABPNN 算法对线夹温度进行预测，最后与PSOBPNN、GA-BPNN、SSA-BPNN、BPNN 算法模型预测结果进行比较，结论如下。

1） 当光照强度每升高200 W/m2线夹温度升高3 K；环境温度每升高1 K 线夹温度均升高1 K；而电流负荷对线夹温度影响较高。因此绝缘跳线夹在夏季高温、高负载率和高日照条件下应多关注其工作状况。

2） ISSA-BPNN 预测模型的收敛速度比SSABPNN、PSO-BPNN、GA-BPNN 预测模型快2 倍，预测误差达到0.71%，准确性相比其他4 种算法更高，决定系数达到0.96。

3） ISSA-BPNN 预测模型的预测误差为0.71%，相比于SSA-BPNN、 PSO-BPNN、 GA-BPNN 及BPNN 较小，该模型能够高效、准确对绝缘跳线夹温度进行预测，为绝缘跳线夹的状态的检测与评估提供依据。