考虑多分布式水电协调运行策略的微电网重构方法

周丹，李嘉杰，邓美玲，李里，李怡雪，尚磊，董旭柱

（1. 广东电网有限责任公司韶关供电局，广东 韶关 512026；2. 广东电网有限责任公司韶关仁化供电局，广东 韶关521339；3. 武汉大学电气与自动化学院，武汉 430072）

0 引言

水电作为可再生清洁能源，能够节能减排、改善环境，其生态效益显著。此外，小水电具有数量广泛、分散布局、就地开发、就近成网的特点，能够明显降低供电成本、经济效益可观。为提高能源系统效率，因地制宜构建以小水电为主力电源的水电微电网为山区负荷进行保供电是必然选择［1-3］。在丰水期时小水电多发甚至满发，小水电与就近负荷组成的微电网处于功率盈余状态，大规模弃水将导致系统经济效益减小。为解决这一矛盾，有效利用水电灵活性资源，挖掘微电网拓扑灵活性潜力，研究水电微电网重构问题具有非常大的研究价值和应用价值。

微电网重构是指通过分接开关和联络开关的开合状态改变达到降低系统网损、平衡负荷、分布式能源消纳等不同运行目标的需求［4-5］。针对微电网重构问题，学者们已经开展了大量研究［6-9］。根据时间断面不同重构问题分为静态重构和动态重构［10-11］。静态重构寻求某个时刻目标函数下的最佳运行拓扑，动态重构考虑多个时间段（一般为24 h）内源-网-荷的互动，较静态重构模型复杂，求解不易。重构求解算法主要分为启发式算法和数学优化算法［12］。文献［13］针对配电网开环运行的结构特点改进粒子群优化算法（particle swarm optimization，PSO）的编码规则，从而保证辐射状约束，减少寻优搜索次数。文献［14］基于图论“避圈法”改进网架编码，缩短PSO 中粒子个体长度，提高可行解的生成概率。综上，改进重构算法需参考图论提出满足辐射状约束的算法策略，提高算法寻优效率。

分布式电源（distributed generator， DG）的接入可改变微电网运行方式、网络潮流，在重构时需考虑DG 对系统运行影响，已有一些文献对DG 在微电网重构中的应用做了相应研究［15-17］。文献［18］提出计及需求响应的配电网重构模型，有效利用需求响应降低配电网重构费用，并减少弃风率、弃光率。文献［19-20］考虑可再生能源的随机性、间歇性以及环境不确定性，借鉴多智能体系统理论，通过各智能体的交互协作提出微网动态重构策略实现微电网个体的即插即用与系统动态重构。文献［21］考虑低风速风电、光伏出力及负荷不确定性，分析了多类型用户行为特征，以三相电流不平衡度和网损最小为优化目标，建立系统动态鲁棒重构模型。文献［22］为解决DG 引起的电压波动提出基于高分辨率DG 出力预测的多目标重构策略，以电压波动和有功网损最小为优化目标，实现系统安全经济运行。然而，现有含DG 的微电网重构文献更多侧重分布式电源的随机性，较少研究DG 间协调互动，并较少研究含分布式水电的微电网重构问题，分布式水电出力策略与微电网重构结合这一方面还有很大研究空间。

在此背景下，本文提出考虑多分布式水电协调运行策略的微电网重构方法以降低弃水率。在微电网重构模型构建方面，分析不同类型水电出力特性后，设计考虑多分布式水电协调运行策略的微电网重构模型；在重构算法方面，基于深度优先搜索算法对传统启发式算法进行改进。通过算例验证可得，所提方法有效提升含多分布式水电的微电网运行灵活性、互动性与运行效率，实现区域资源优化配置，对微电网规划设计相关研究具有借鉴价值。

1 含多分布式水电的微电网模型

1.1 分布式水电模型

水电是目前技术最成熟、储能规模最大且最为经济的储能方式。根据发电功率是否可调节、有无调节水库，水电站分为可调频水电站和径流式水电站。可调频水电站存在水库，发电功率可调节，库容模型如图1 所示。径流式水电无功率调节能力，存在弃水量［23-24］。

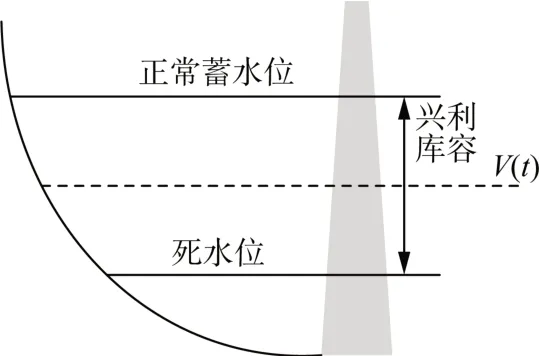
图1 可调频水电站库容示意图Fig. 1 Schematic diagram of storage capacity of adjustable frequency hydropower station

水电机组的出力大小与水电机组的发电流量、水库库容、水头和水轮发电机组的转换效率有关。水电机组的水头随着水库水位的变化而变化，忽略水头损失影响，水轮机功率输出还需要考虑发电机的转化效率，计算公式如式（1）所示。

式中：Php（t）为水电站t时段下实际有功出力；K为水电站发电机组转换效率；Ff（t）为水电站在t时段下的平均发电流量；H（t）为t时段在水库上游水位；He（t）为水库在t时段尾水位。

水库蓄水量主要与上游流入水库的来水流量、用于发电的发电流量和弃水量有关，计算公式如式（2）所示。

式中：V（t）为水库t时刻开始时库容；V（t+1）为水库t时刻结束时库容；Vr（t）和Fr（t）分别为t时段内入库水量和入库流量；Vf（t）和Ff（t）分别为t时段内水电机组发电消耗的水量和发电流量；Vd（t）和Fd（t）分别为t时段内水库弃水量和弃水流量；Δt为时间间隔。

水库的上游水位和水库库容，尾水位和水电机组发电流量存在非线性关系，可进行线性化拟合［23］：

式中：G1（·）为水库上游水位和水库库容之间关系；G2（·）为水库尾水位和水电机组发电流量之间函数关系。

1.2 多分布式水电协调运行策略

在丰水期，分布式水电出力远大于负荷需求，为充分利用资源，降低弃水量，本文提出多分布式水电协调运行策略。微电网区域内含多类型分布式水电，优先径流式水电站发电。针对径流式水电，目标为降低弃水量；针对可调频水电站，目标为预留更多可用库容。策略流程如图2 所示，其中：M为微电网中可调频水电站数量；N为微电网中径流式水电站数量；Pph，i为第i台可调频水电站出力；Php，j为第j台径流式水电站出力；PL为微电网总负荷；Php，is为当前入库流量下可调频水电站最大出力；Php，ir为可调频水电站额定发电功率；Php，js为当前入库流量下径流式水电站最大出力；Php，ir为径流式水电站额定发电功率。

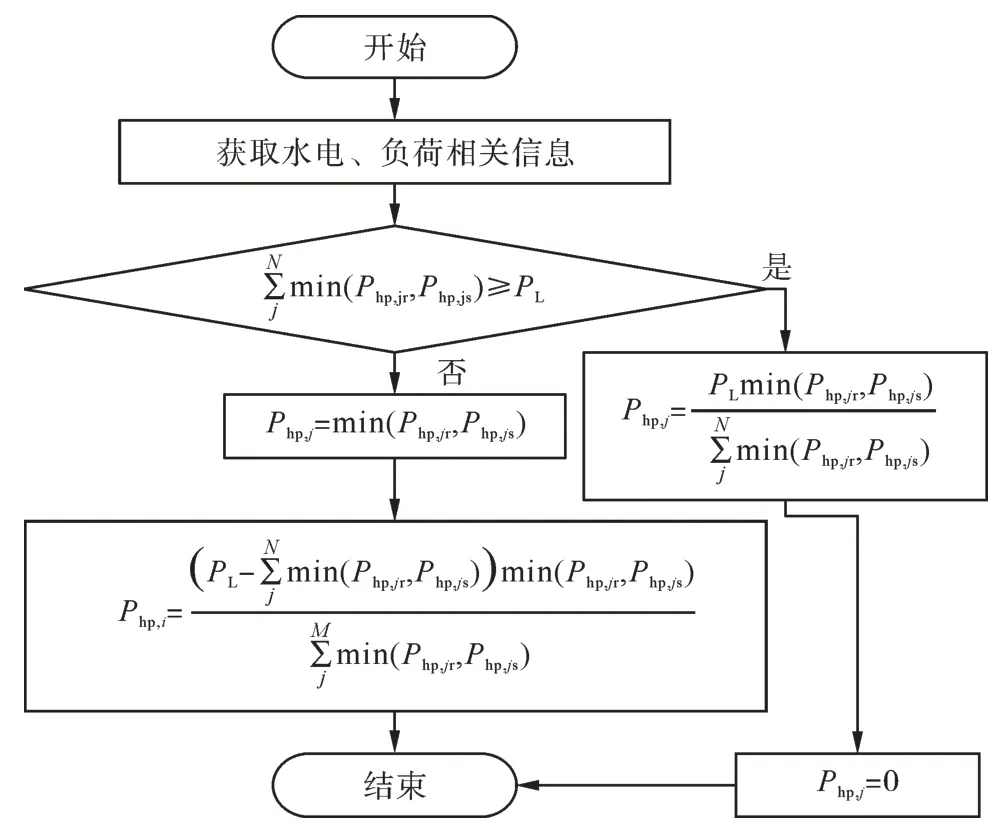
图2 多分布式水电协调运行策略流程Fig. 2 Flow chart of multi-distributed hydropower coordinated operation strategy

运行策略步骤如下。

1） 获取水电、负荷相关信息。

2） 水电额定发电功率和当前入库流量下最大出力的较小值为当前水电最大可能出力，判断当前径流式水电最大可能出力是否能满足负荷。

3） 径流式水电最大可能出力能满足负荷，按照各径流式水电最大可能出力的比例分配径流式水电出力，弃掉多余来水量，调频式水电出力为0。

4） 径流式水电最大可能出力不能满足负荷，径流式水电出力取当前最大可能出力，按照各调频式水电最大可能出力的比例分配调频式水电出力。

多分布式水电出力需满足：

1.3 网架拓扑数学模型

将微电网抽象成由支路和节点组成的图G，进行微电网系统拓扑建模。对于图G=（V，E），由点集V=｛vi｝和边集E=｛ek｝构成的二元组，V中元素vi为顶点，对应微电网的节点；E中元素ek为边，对应微电网的支路。其中V=｛v1，v2，…，vq｝，构造矩阵图G的邻接矩阵A=（aij）m×m，其中m为节点总数，矩阵A的元素aij如式（6）所示。

2 含多分布式水电的微电网重构模型

2.1 优化目标

本文研究以一天为开关动作周期的微电网重构模型，考虑一天内的多水电协调运行和负荷情况。日前收集水电、负荷信息以支撑重构方案的生成。从经济性出发构建以线路有功损耗最低为目标函数，如式（7）所示。

式中：l为支路序号；αl为第l条支路闭合状态，取1 为支路闭合，反之取0；rl为第l条支路电阻；Ul为第l条支路末端节点电压有效值；Pl、Ql分别为第l条支路末端流过的有功功率和无功功率。

2.2 约束条件

1）潮流约束

式中：ui、uj分别为节点i和节点j的节点电压；Pi、Qi分别为节点i注入的有功功率和无功功率；PLi和QLi分别为流过负荷节点i的有功功率和无功功率；Gij为节点i和节点j之间的电导值；Bji为节点i和节点j之间的电纳值；θij为节点i和节点j之间的相角差。

2）节点电压约束

式中Umin、Umax分别为节点最低电压限值和节点最高电压限值。

3）容量约束

式中：Sl为流过支路l的实际功率值；Slmax为流过支路l的最高功率。

4）水电机组出力约束

水电机组有功功率约束、无功功率约束如式（12）—（13）所示。

式中：Pph，min、Pph，max分别为水电最大有功出力、最小有功出力；Qph，min、Qph，max分别为水电最大无功出力、最小无功出力。

水库库容约束如式（14）所示。

式中Vmin、Vmax分别为水库最小库容、最大库容。

5）辐射状拓扑结构约束

3 微电网重构求解算法

本文提出的微电网重构模型为强非线性模型，利用传统的数学规划方法不易求解，而启发式算法在寻优过程中自动获取搜索空间的知识，动态有效降低问题的复杂性，其中粒子群算法为常见启发式算法之一。现有较多文献研究改进粒子群算法，主要体现在对惯性权重模型改进、带邻域操作、协同计算等方面，从而提高算法本身的搜索效率。然而微电网重构过程中开关随机开断将大概率生成不可行解，其网络拓扑包含孤岛或回路。因此，本文结合重构特点，提出一种基于改进PSO 的微电网重构求解算法采用深度优先搜索算法保证网络拓扑的辐射性和连通性，该算法容易实现、运算速度快，改进方向更具针对性。采用二进制编码PSO 描述微电网开关状态，0 表示该位对应的开关打开，1 表示该位对应的开关闭合。为避免寻优过程中产生大量不可行解，本文基于深度优先搜索算法改进粒子生成和位置更新，保持迭代过程中网络满足辐射状约束，以提高算法的搜索效率。深度优先算法是一种用于搜索树或图的算法，可以找寻节点之间的无向通路，详细步骤见文献［25］。本文提出的重构求解算法步骤如下。

1） 设置种群大小、最大迭代次数和最小误差阈值。

2） 基于深度优先搜索算法随机产生可行解，计算每个粒子的适配值（即优化目标值）将其作为初始个体极值pbest，i，将所有pbest，i中的最小值赋给gbest作为初始全局极值。

3） 迭代次数T=1。

4） 生成［0，1］区间上的随机数γ，当γ>0.5时，设置个体极值为参照粒子；当γ≤0.5 时，设置全局极值为参照粒子。本文提出粒子更新策略，策略流程如图3 所示。以6 节点系统为例，进行粒子拓扑更新，如图4 所示。在参照粒子中随机选取两节点，即节点4、节点6，通过深度优先搜索算法获取无向通路，形成支路集合｛e26，e25，e45｝，遍历支路集合改变支路e45、e34和e36通断，得到更新后粒子。依据粒子更新策略更新粒子后，计算更新后粒子适配值。

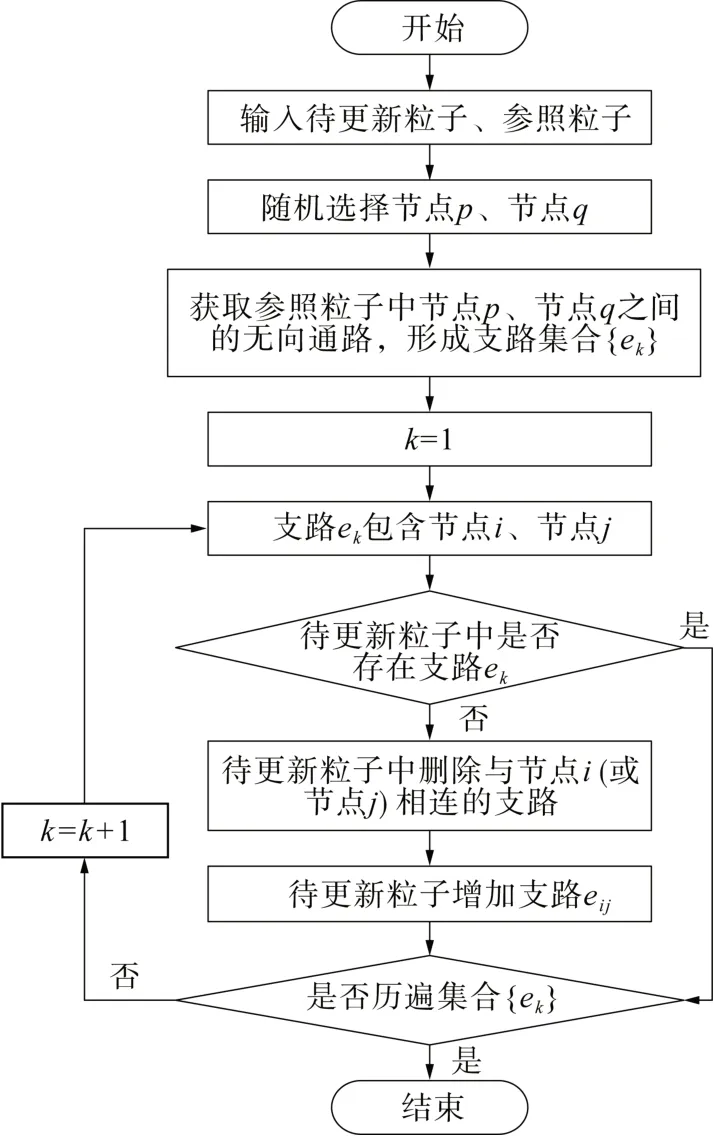
图3 粒子更新策略Fig. 3 Particle update strategy

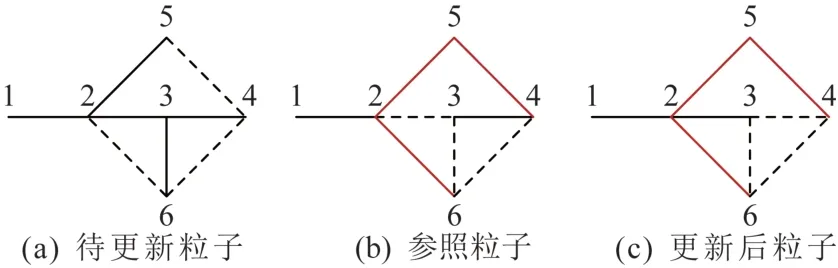
图4 粒子更新示意Fig. 4 Schematic diagram of particle updating

5） 如果满足收敛条件或达到最大迭代次数Tmax，则停止计算，否则继续寻优。

6） 如果粒子i的适配值优于此前的个体极值pbest，i，则将其值设为pbest，i；如果最佳的pbest，i优于此前的全局极值gbest，则将其值设为gbest。

7） 迭代次数T=T+1。

8） 如果迭代次数到达上限即可结束寻优；否则返回步骤4）。

4 算例分析

本文在IEEE 33 节点系统中测试，实现含多分布式水电的微电网重构。其网架结构如图5 所示。微电网为孤岛运行模式，包含3 台可调频水电站、3 台径流式水电站，机组参数如表1—2 所示。其中，将水电站上流水位-库容关系、尾水位-发电流量关系进行线性化拟合。总有功负荷峰值为3 715 kW，总无功负荷峰值为2 300 kvar，典型日负荷曲线如图6 所示。设置基准容量为1 MW，基准电压为12.66 kV，节点电压允许范围为0.95~1.05 p. u.。本算例中，假设水电站的自然入库流量为确定的，且不同分布式水电入库流量相同，入库流量曲线如图7 所示。设置可调频水电站初始水位为25 m，水位上下限为0、30 m。

表1 IEEE 33节点系统中分布式水电信息Tab. 1 Distributed hydropower information in IEEE 33-node system

表2 分布式水电发电、库容信息Tab. 2 Distributed hydropower generation and storage capacity information

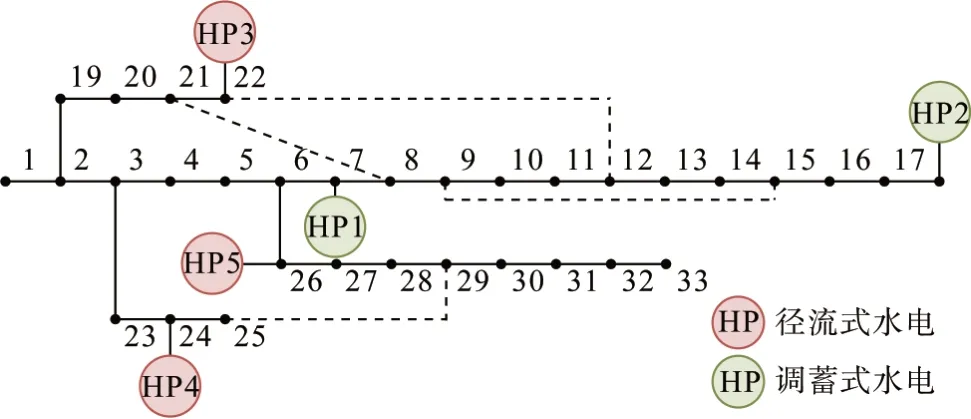
图5 IEEE 33节点系统图Fig. 5 Diagram of IEEE 33-node system

为验证所提考虑多分布式水电的微电网重构模型的有效性，本文设置4种场景，包括：1） 考虑多分布式水电协调运行的微电网重构前；2） 考虑多分布式水电协调运行的重构后；3） 分布式水电独立运行的微电网重构前；4） 分布式水电独立运行的微电网重构后。

表3 列出了4 种场景下微电网拓扑结构、有功网损和弃水量。由表3 可知，考虑水电协调运行策略可大幅降低微电网弃水量。相比各水电独立运行，考虑水电协调运行策略的微电网弃水量要降低约50%。以系统网损为优化目标进行微电网重构，有效提高系统经济性。不同水电运行策略下，有功网损均大幅减小。考虑水电协调运行策略的微电网重构后网损降低82.27%，各水电独立运行的微电网重构后网损降低72.7%。虽然考虑水电协调运行的微电网重构后的有功网损大于各水电独立运行的微电网重构后的有功网损，但是，考虑水电协调运行的微电网弃水量远小于各水电独立运行的微电网弃水量。综上，本算例中考虑水电协调运行策略的微电网重构方案具有优良的综合性能，本文提出的考虑多水电协调运行策略的微电网重构方法具有可行性。

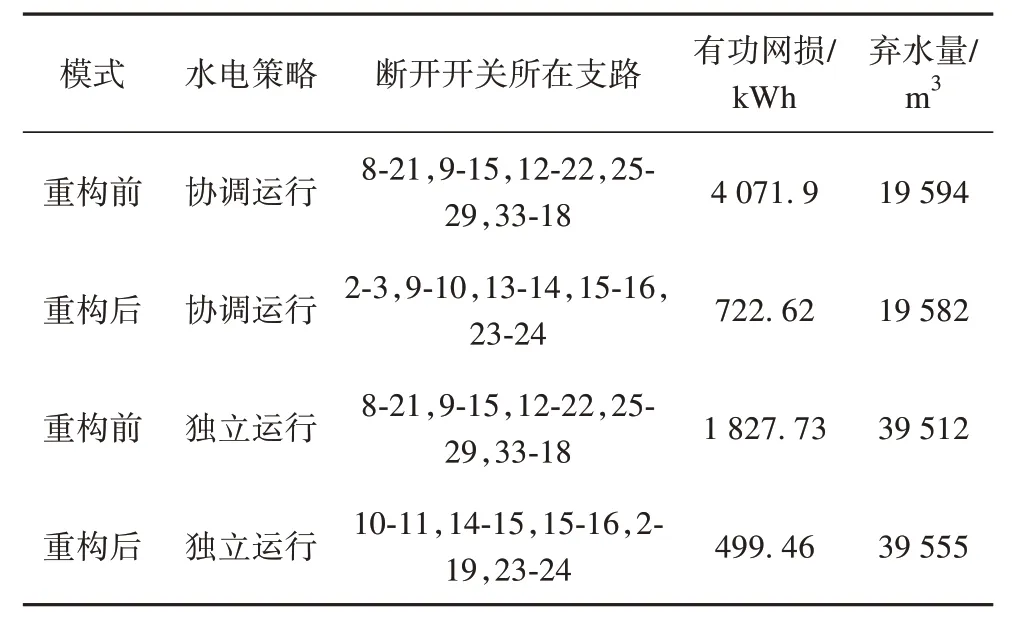
表3 微电网重构结果Tab. 3 Microgrid reconfiguration results

进行微电网重构前后的节点电压分布如图8 所示，由图8 可以看出，重构后的节点电压总体高于重构前，该配电网的各节点电压得到显著改善。在提升微电网运行经济性的同时也提高了电压质量。重构后考虑多水电协调运行的微电网最低电压标幺值为1.03，出现在节点30。重构后部分节点电压低于重构前节点电压，例如节点14、节点15，由于断开开关13-14、15-16，节点14、节点15变为线路末端节点，电压相对降低约0.27%。

图8 节点电压分布（时刻19）Fig. 8 Node voltage distribution (Time19)

考虑多水电协调运行策略的微电网重构方案的水电站水位变化曲线如图9 所示。由于本文场景发生在丰水期，设置入库流量大，在仿真周期内可调频水电站的水库水位缓慢增加，并在13 点时达到水库上限。此外，本方案的水电站出力曲线如图10所示。在该策略下，各径流式水电出力相同，全天满发，各可调频水电出力相同，且随负荷波动。

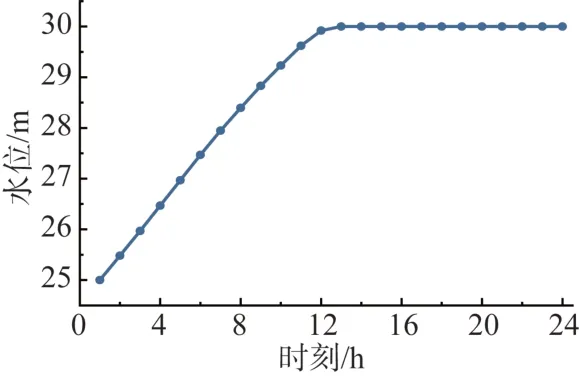
图9 可调频水电站水位变化曲线Fig. 9 Variation curve of water level in adjustable frequency hydropower station

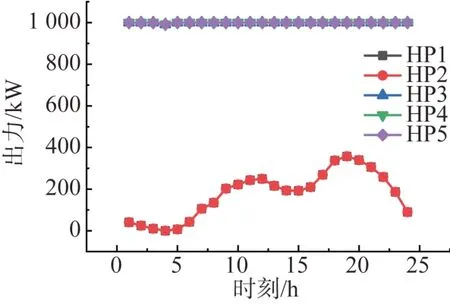
图10 多分布式水电站出力曲线Fig. 10 Output power curves of multi-distributed hydropower station

本文算例中设置粒子数为50，迭代次数为150次。对比传统PSO 算法，进行了50 次重复实验，基于改进PSO 的重构算法平均仿真时间为13.21 s，基于传统PSO 的重构算法平均仿真时间为13.87 s，收敛曲线如图11 所示。可知，相较于基于传统PSO 的重构算法，基于改进PSO 算法可快速收敛至全局最优，具有收敛速度快、迭代次数少等特点。

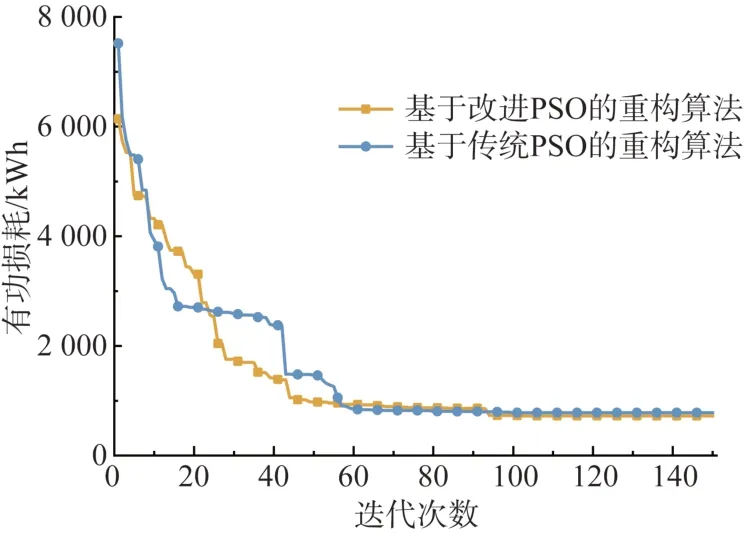
图11 两种算法迭代次数曲线Fig. 11 Iteration number curves of two kinds of algorithms

5 结语

本文提出一种基于库存容量约束的多水电协调运行策略及其微电网重构模型，并基于改进PSO 的重构算法实现模型的有效求解，得出微电网重构方案。结果表明，本文提出的多水电出力协调策略可有效提升降低弃水量，所改进PSO 算法在配电网重构求解方面优于传统PSO 算法，可更加有效地避免陷入局部最优、提高算法寻优效率。

本文所提的一种考虑多分布式水电协调运行策略的微电网重构方法可行，且重构算法具有收敛速度快、广泛适用等特点，可灵活改变微电网拓扑，有效降低微电网有功损耗，降低弃水量。

本文从不同方面充分挖掘微电网灵活性资源潜力，改善微电网特性。通过微电网重构调节网架结构，充分发挥网架拓扑的灵活性；提出多分布式水电协调运行策略，充分挖掘可调频水电的虚拟储能特性。

下一步将考虑枯水期或平水期的情况，构建水电微电网重构模型，在源小于荷和源荷相近的情况下满足重要负荷供电，提升含分布式水电的微电网韧性水平。