压力角对鼓形齿联轴器齿面承载性能的影响

李厚超，王建梅，管永强，张文震

(太原科技大学 重型机械教育部工程研究中心，山西 太原 030024)

0 前言

鼓形齿联轴器广泛应用于船舶、冶金、轧钢、轨道交通等领域[1]，有补偿两轴相对位移、承载能力强、运转平稳等优点。鼓形齿的啮合相较于普通的齿轮啮合更复杂，设计时内外齿轮具有较大的间隙来保证在不对角的工况传递转矩，在相同的工况下，承载能力比普通的渐开线直齿联轴器高15%到20%左右[2]。因此，研究鼓形齿的承载性能对于其可靠设计有着十分重要的作用。

国内外学者对鼓形齿的齿形设计、几何啮合、负载分布、动力学和磨损强度分析等方面做了大量工作[3]。由于鼓形齿联轴器的轮齿参数对承载性能的影响有待于进一步探究，因此国内外对于联轴器的标准均无明确轮齿的设计参数[4]。Yabin Guan等[5]基于微分几何和啮合理论，建立了考虑不对中角的鼓形齿联轴器的数学模型和承载齿面接触分析方法，计算了不同偏差角下的最小周向间隙、接触位置和接触应力。Keum[6]通过有限元方法分析了鼓形齿联轴器齿面接触应力在位移圆半径、齿数和模数的变化下的影响规律。肖来元等[7]测试了不同齿面弧度轮齿接触情况，对比发现共轭鼓形齿有很好的接触性能，刘笃喜等[8]提出压力角对齿廓的弹性变形比齿面直径影响大。王孝义等[9]提出一种含过渡齿套鼓形齿联轴器分析了其啮合力学特性。朱文文等[4]研究了多组压力角的鼓形齿联轴器的齿面接触应力和米塞斯应力，但是压力角的梯度太小且没有考虑不对中角的影响。选择合适的鼓形齿压力角对于确保齿轮传动具有足够的齿面承载性能非常重要。因鼓形齿联轴器较普通齿式联轴器复杂，本文探究了不对中角下和间隙工况下压力角对齿面承载性能的影响。

鼓形齿联轴器的承载性能分析方法有解析法、数值法和试验法[10]。数值法是通过计算机仿真和数值计算来模拟和分析齿轮传递系统的承载能力，可以考虑更加真实和复杂的工况材料和几何参数，更加详细的参数、变形等。因鼓形齿联轴器运动的复杂性，选用数值法进行求解。

本人通过Solidworks软件建立鼓形齿无间隙的单齿模型和有齿面间隙全齿模型。利用有限元软件ANSYS分析了不同压力角的齿面等效应力。研究不同不对中角的工况压力角在对于鼓形齿联轴器齿面承载性能的影响，包括全齿模型不同工况轮齿接触的对数、鼓形齿齿面的应力分布规律。研究结果可为鼓形齿联轴器的结构设计提供一定的参考。

1 鼓形齿联轴器模型建立

1.1 鼓形齿联轴器工作原理

鼓形齿联轴器是一种复杂的机械传动装置由内齿圈和外齿轴套组成可移式联接，内齿圈通过传动筒体或传动轴联接，或者采用螺栓联接[11]。在实际运转中，鼓形齿联轴器的啮合运动呈现复合运动的特性，在一次旋转过程中轮齿穿过纯翻转区、纯摆动区，然后回到纯翻转区。将各齿沿分度圆圆周展开，可得到轮齿的相对位置[12]，如图1所示。

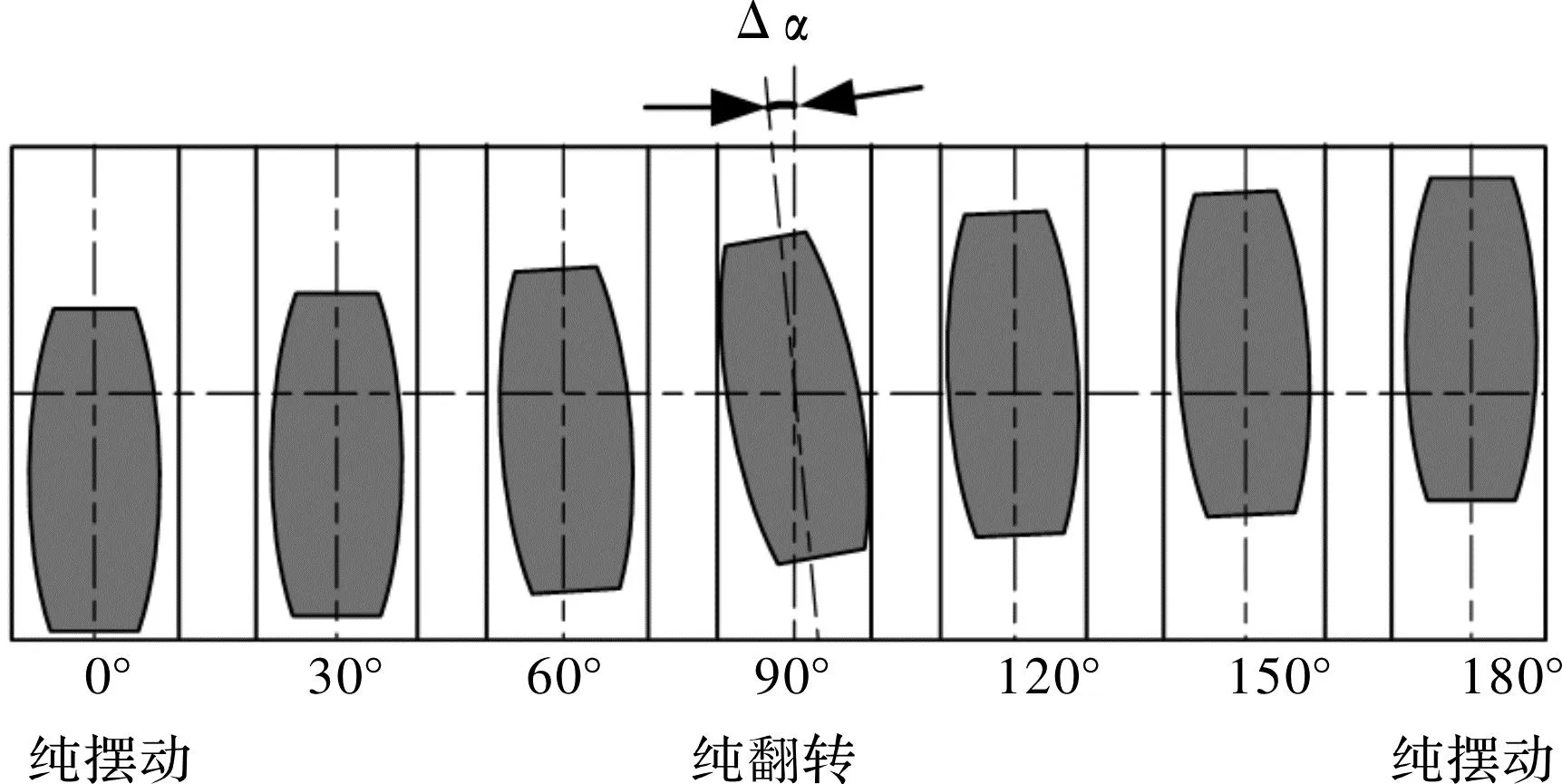
图1 轮齿的相对位置

1.2 鼓形齿联轴器三维模型的建立

压力角作为决定鼓形齿联轴器齿廓的关键参数，结合实际应用选定五组压力角，分别为20°、23°、25°、28°和30°[13]，鼓形齿联轴器位移圆半径R结合承载能力计算，按照式(1)[14]确定：

R=(0.5～2.0)d

(1)

式中，d为鼓形齿分度圆直径，此处系数选择0.9。

鼓形齿联轴器的内齿和外齿之间存在间隙J，最小理论法相间隙按照式(2)[14]确定：

(2)

式中，φt是鼓形齿曲率系数，通过查表[14]可得；Δα为不对中角；α为鼓形齿压力角。

在模拟鼓形齿的实际工况时，确保加工制造过程中间隙精确控制显得尤为关键。在进行有限元仿真时，需要考虑对制造误差进行补偿[14]。鼓形齿联轴器的设计参数见表1。

表1 鼓形齿联轴器的设计参数

为减少有限元计算量，考虑鼓形齿的仿真要求，将鼓形齿联轴器的整体模型进行合理简化，沿齿宽的方向进行截取，只保留内齿圈和外齿轴套[15]。单齿模型在全齿模型简化的基础上截取。

利用GearTrax软件和Solidworks软件建立了鼓形齿联轴器的内齿圈和外齿轴套的三维模型和简化模型，见图2。

图2 鼓形齿联轴器三维模型

1.3 鼓形齿联轴器有限元模型的建立

1.3.1 有限元网格划分

将模型导入ANSYS对鼓形齿三维实体模型进行网格划分，网格类型选用 Solid185，该网格类型在有限元分析中表现出良好的稳定性和收敛性。它对于复杂的结构和边界条件具有较好的适应性，能够提供可靠的分析结果。齿轮啮合的接触面内齿圈控制在3 mm，外齿轴套控制在2 mm。共划分116 336个单元、150 650个节点。鼓形齿联轴器的材料选择42CrMo，弹性模量为2×105MPa，屈服极限为930 MPa，泊松比为0.3。有限元模型见图3。

图3 有限元模型网格

1.3.2 边界条件

其不对中角的工况选取了四组，分别为0°、0.5°、1°、1.5°不同压力角的鼓形齿联轴器按照以上述四组不对中角进行分析。对鼓形齿联轴器的啮合面的接触对进行设置，共设置48个接触对。接触状态设置为摩擦，摩擦系数为0.1。创建转动副。内齿圈外圆柱面设立一个转动副，在其面上施加50 kN·m的转矩，在外齿轴套的内圆柱面设立一个转动副，在其面施加一个1 rad/s的转速，两个运动副方向相反，模拟鼓形齿联轴器运转。

2 仿真结果与分析

现将48个齿从1到48进行编号，提取等效应力，编号如图4所示。轮齿的运动属于复合运动，当不对中角变化时不同压力角的鼓形齿联轴器的接触齿对数发生变化。不同齿面间的等效应力不相同，应力分布呈对称的形式，当两个旋转角度之差为180°时等效应力和相对滑动距离均关于轴线对称。如图4所示，q关于n/2+q对称[12]，故只分析180°范围内的轮齿受力，也就是分析24个轮齿的受力即可。

图4 轮齿编号

如图5所示，鼓形齿联轴器0°时外齿圈齿面的等效应力在齿根附近最大[16]，齿顶部分也有小幅度的应力集中。在0.5°、1.0°和1.5°时应力集中点对于0°均有一定的相对滑动。不对中角增加，轮齿的应力集中点偏移量变大。

图5 等效应力分布

如图6所示，是以轮齿齿面中间为基准，对不同压力角单齿模型提取最大等效应力值点到基准轴的水平距离，不同压力角的鼓形齿齿面在相同不对中角所呈现的位移。

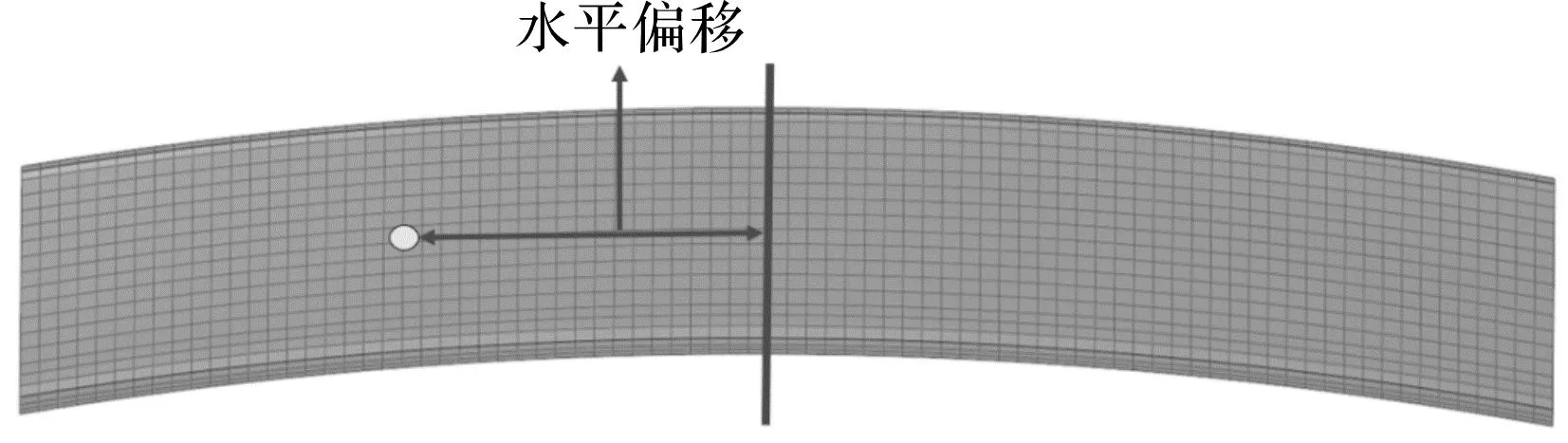
图6 最大等效应力点位移提取

如图7所示，为当不对中角为0.5、1°和1.5°时，最大等效应力值点较于基准的水平位移。

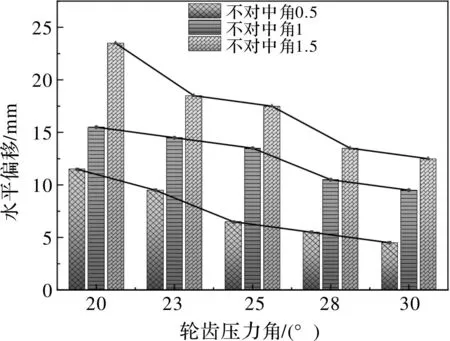
图7 最大等效应力点偏移距离

可看出：在同一不对中角的工况下，压力角增大偏移量减小；三组不对中角工况下，压力角对于最大应力值点的偏移量的影响趋势都是线性的。偏移量越小轮齿的对中效果越好，对齿面的承载能力和接触齿对数起积极的作用，同时，大压力角的最小设计齿宽小于小压力角。

在不对中角为0°时其相对滑动距离为0，鼓形齿联轴器的啮合为全啮合。当不对中角大于0°时，相对滑动距离随着不对中角的增大而增大，不对中角0.5°时因相对滑动距离较小仍为全齿啮合。在50 kN·m的转矩工况下，不对中角为1°和1.5°时，图8为不对中角为1°和1.5°时齿的接触齿对数。同一不对中角工况下，当不对中角增加时，其压力角对于鼓形齿联轴器的接触齿对数的影响明显，当压力角增加时齿的接触齿对数呈增加的趋势[17]，当不对中角增加接触齿的对数减少。1°时所有的压力角的接触齿对数均大于1.5°时的所有压力角鼓形齿联轴器的接触齿对数。

图8 接触齿对数

不对中角为0°时，即理想对中情况下，因为是全齿啮合且各接触齿对没有相对位移，全齿模型每个齿的等效应力和大致相等，故提取单齿和全齿的最大等效应力值，见图9。

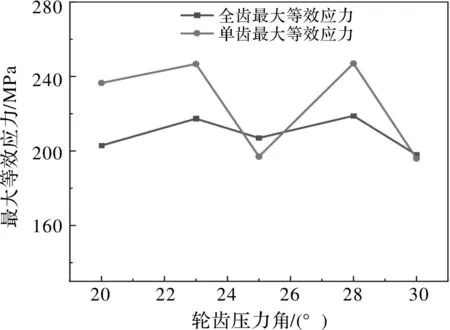
图9 0°不对中角单齿和全齿齿面最大等效应力

可得出：在不对中角0°时全齿模型和单齿模型等效应力与压力角的规律相同，全齿模型当压力角为30°时其齿面承载能力比其他四组压力角的齿面承载能力高，全齿模型中30°较28°等效应力差值大约为20 MPa，占比约9%。单齿模型中等效应力最小值30°时较最大值28°时的差值约为21 MPa，占比约20%。在考虑间隙的情况下，不同压力角下的等效应力相差很小。无间隙的情况下轮齿的齿面承载性能呈非线性的关系。

1°与1.5°齿面之间会发生相对位移，导致接触齿对数会发生变化，不同齿之间最大等效应力会发生变化。根据图4中的轮齿编号提取不对中角1.5°工况下五组压力角的每个齿面最大等效应力；全齿模型受力最大齿的齿面等效应力和单齿模型的最大等效应力进行对比，见图10。

在1.5°不对中情况下接触齿对数见图8，压力角30°是接触齿对数最多的，25°和28°接触齿对数相同，图10(b)在25°到28°的线段斜率最小，与其接触齿对数的斜率所对应，接触齿对数影响齿面承载性能，图10(b)中在除30°时单齿模型的等效应力大于全齿模型的等效应力值，全齿模型在30°时等效应力较28°时差值为36 MPa，等效应力增大了大约7.6%。总体趋势是压力角增大对齿面承载性能起改善作用。因单齿模型是不考虑间隙，全齿模型是参考的经验公式。间隙的计算并不准确，故间隙的精准控制对齿面的承载性能的改善十分重要。

纯翻转区接触齿面上的接触点位置将会发生明显的偏移[18]，使得纯翻转区轮齿的受力较大。另一方面较大的鼓形齿压力角会使齿轮齿面的接触区域增大，分布更均匀，从而提高齿轮的承载能力。这是因为较大的鼓形齿压力角会使齿面接触处的应力分布更为均匀，减小了局部应力集中的程度，降低了齿面的接触应力。

3 结论

本文对鼓形齿联轴器进行了简化，通过有限元分析软件Ansys，对比了不考虑间隙单齿和考虑间隙全齿的啮合面的等效应力，分析了受载时齿面的等效应力以及在此工况下接触齿的对数。

研究了四组定不对中角的工况，当不对中角为0°时，考虑间隙时不同压力角的齿面等效应力下相差不大，故对于鼓形齿联轴器齿面承载能力的影响不大[19]。不考虑间隙时，压力角对于齿面承载性能是非线性的。

当鼓形齿联轴器的不对中角增加时，接触齿对数减少。在同一工况下，接触齿对数随着压力角的增大总体呈上升趋势，同时接触齿对数影响齿面承载性能。

不考虑间隙时，轮齿的压力角增大对于齿面承载性能是有利的，压力角增大齿面承载性能增强，考虑间隙时的情况下，齿面承载性能先增大后减小。

在今后的研究中，将建立鼓形齿联轴器的齿面数学模型，通过数学模型计算轮齿的间隙，通过计算的间隙探究鼓形齿联轴器的几何参数对齿面承载性能的影响。