不锈钢管再生混凝土短柱轴压力学性能研究

马海兵, 胡永胜, 张文浩, 赵 晖*, 沈玲华

(1. 山西平榆高速公路有限责任公司,山西 太原 030000; 2. 太原理工大学 土木工程学院, 山西 太原 030024)

不锈钢因其外表美观、耐久性好、耐火性好且维护费用低等优点,在高标准的结构耐久性建筑中具有广泛应用前景.而废弃混凝土破碎形成的粗骨料拌和得到再生粗骨料混凝土作为建筑废弃混凝土高效再利用的有效途径,但再生混凝土因其劣化的力学性能导致应用受限.因此,在不锈钢管中填充再生混凝土组合而成的不锈钢管再生混凝土(RA-CFSST)可有效改善管内再生混凝土的脆性并提高再生骨料的利用效率.

目前,国内外学者[1-6]对不锈钢管混凝土构件(CFSST)的轴压力学性能进行了相关试验和有限元研究,在与碳素钢管混凝土构件相比下,CFSST构件在轴向应变较大时表现出更好的延性.Yang等[7]通过圆形和方形不锈钢管再生混凝土短柱的轴压力学性能试验,考虑不同再生粗骨料取代率(0%、25%、50%与75%)影响,研究认为RAC-FSST的刚度与承载能力随着取代率的增加而下降,相较于CFSST构件,其承载力降低约6.1%～18.0%.Tam等[8]、Zhang等[9]基于轴压试验,认为100%取代率的不锈钢管再生混凝土构件刚度明显降低,峰值应变增大.然而,由于再生粗骨料较低的弹性模量和表面残余砂浆的存在,再生混凝土受不锈钢管约束作用机理尚不明确,轴压过程中钢与混凝土的应力状态发展需要进一步明确.因此有必要对不锈钢管再生混凝土轴压力学性能进行机理与扩大影响参数分析,给出相关设计建议.表1为已有不锈钢管再生混凝土短柱轴压力学性能研究相关参数.

表1 相关研究试验参数

为此,基于前期试验,本文采用有限元ABAQUS软件对不锈钢管再生混凝土短柱轴压力学性能进行分析.重点研究该类构件在轴压作用下各部件的应力状态发展、钢-混凝土之间的接触应力等机理,并分析再生混凝土强度、粗骨料取代率、不锈钢类型以及含钢率对其轴压承载力的影响.采用国内外现有钢管混凝土结构设计规范进行适用性对比,为该类构件的工程应用推广提供参考.

1 有限元模型建立与验证

1.1 材料模型

不锈钢泊松比μs和弹性模量E0分别根据文献试验实测值确定.当缺乏实测值时,μs取为0.3,E0取为200 GPa.应力-应变关系采用Rasmussen[10]建议的模型,如式(1～3)所示:

(1)

式中:σ0.2为残余应变0.2%对应的应力;E0和E0.2分别为不锈钢弹性模量和残余应变0.2%处的割线模量;n和m为应变硬化指数;其余各参数的含义见文献[11～12].

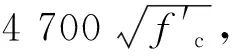
(4)

(5)

y=σ/σ0

(6)

σ0=f′c

(7)

(13)

1.2 单元类型、网格划分与界面模型

外包不锈钢管采用S4R缩减积分壳单元,核心再生混凝土和端板均采用C3D8R线性缩减积分实体单元.不锈钢管与混凝土接触面法向采用“Hard Contact”,切向采用库伦摩擦模型来表征界面切向力的传递性能,摩擦系数取为0.25[16-17].端板与不锈钢管采用“Tie”接触模拟实际焊接.建立的轴压短柱构件的有限元模型通过施加整体坐标系下U3方向的平动实现轴向压力的加载,同时限制端板在整体坐标系中U1、U2方向平动自由度与绕x、y、z轴(UR1、UR2和UR3)的转动自由度.将端板外侧耦合至各面中心参考点,通过对该参考点的自由度限制与施加位移实现轴向加载.经过网格敏感性分析,当网格尺寸取为20 mm时,计算结果达到较好的精度与计算效率.图1为有限元模型示意图.

图1 有限元模型示意图Fig.1 Finite element model

1.3 模型验证

为验证有限元模型的准确性,对Yang等[7]、Tam等[8]和Zhang等[9]进行的32个不锈钢管再生混凝土短柱轴压试验进行验证.典型试件模型计算与前期试验试件荷载(N)-应变(εv)曲线对比如图2所示.由图可知,本文有限元模型可以较好的预测RA-CFSST构件荷载-应变曲线的发展.图3为所验证试件极限承载力模拟值Nu,FE与试验值Nue的对比,Nu,FE/Nue的平均值和方差分别为0.951和0.025.图4进一步给出了典型试件H-114-100-1试验破坏模态与有限元模拟结果的对比,可见有限元模拟结果与试验结果吻合较好.

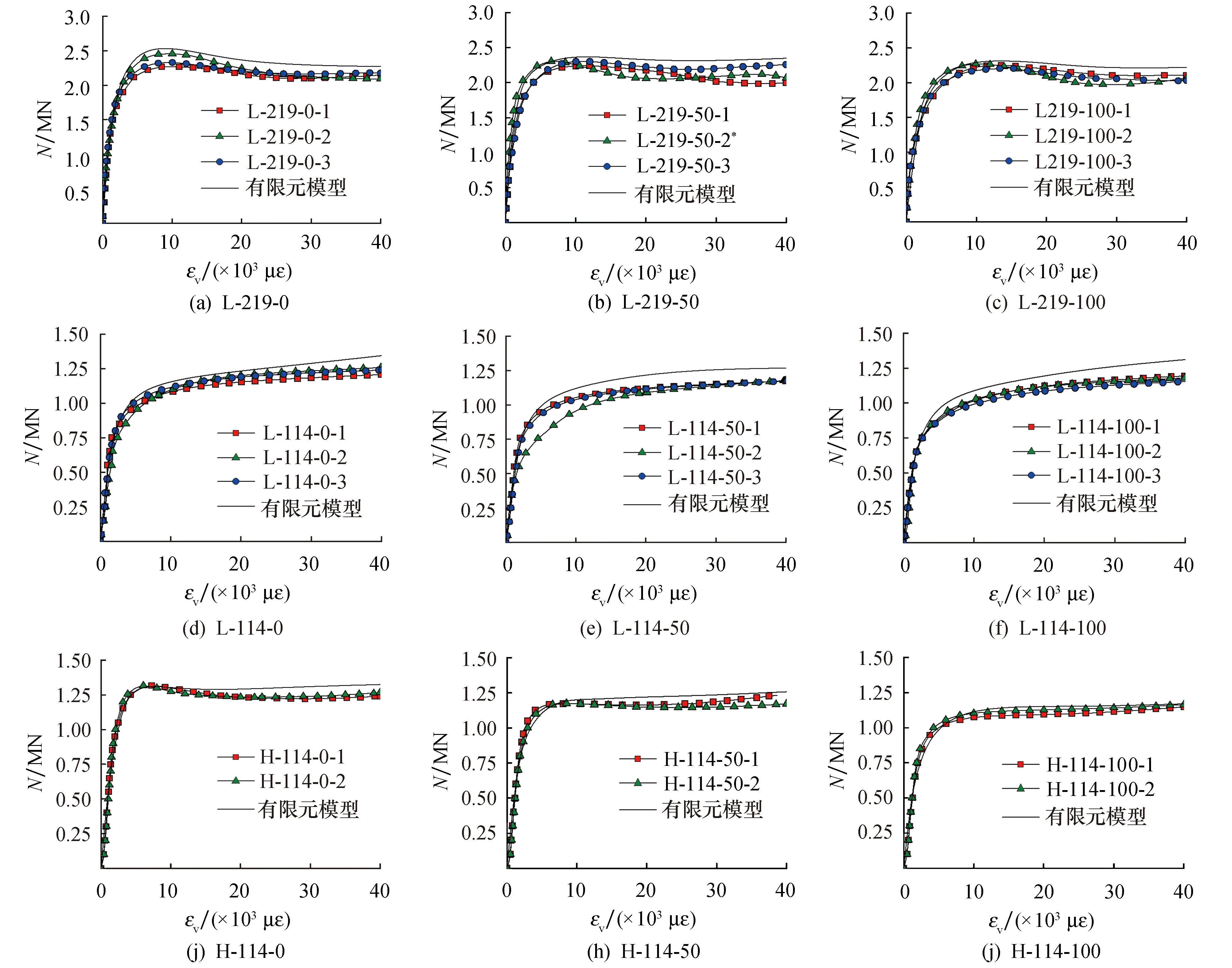
图2 有限元计算结果与试验荷载-应变曲线对比

图3 有限元计算极限承载力与试验值对比Fig.3 Comparisons from FE and tested ultimate strengths

图4 破坏模态对比Fig.4 Comparisons from FE and tested failure pattern

2 受力全过程机理分析

为研究不锈钢管再生混凝土轴压短柱的受力全过程机理,以RA-CFSST典型构件(D=400 mm,t=7.1 mm,L=1 200 mm,r=50%,α=7.5%,fcu=50 MPa,σ0.2=220 MPa)为例,对各部件应力状态发展、应力分布、钢-混凝土接触应力变化规律进行分析.

2.1 应力状态发展

图5给出了RA-CFSST典型构件截面平均应力(σm)、再生混凝土纵向应力(σc,v)、不锈钢管纵向应力(σs,v)与环向应力(σs,c)随轴向应变(εv)变化的关系曲线.根据曲线发展可分为4个阶段:

1) OA段:此阶段各曲线均线性增长,再生混凝土与不锈钢管均处于弹性阶段,不锈钢环向应力较小,表明钢材正处于单向轴压状态.从A点起,试件开始进入弹塑性阶段,此时不锈钢管纵向应力约为其名义屈服强度的50%～60%[18].

2) AB段:此时构件处于弹塑性阶段,再生混凝土应力-应变曲线呈现非线性增长趋势;不锈钢管纵向应力先增后减,环向应力显著增加,钢材在此阶段达到其名义屈服强度,不锈钢管开始对核心混凝土产生约束作用.当达到极限承载力时(B点),核心再生混凝土的纵向应力大于单轴压缩状态下的峰值应力(f′c),表明外钢管的约束作用能够有效提高核心再生混凝土的强度.

3) BC段:钢材进入强化阶段,其纵向应力逐渐减小至较为稳定水平,环向应力持续增加.在外包不锈钢管的约束作用下,核心再生混凝土纵向应力缓慢增加,但随着外钢管发生局部屈曲,约束效应减弱,呈现延性特征.

4) CD段:不锈钢管纵向应力、再生混凝土纵向应力与截面平均应力稳定发展,不锈钢管的环向应力缓慢增加,构件进入后强化阶段.

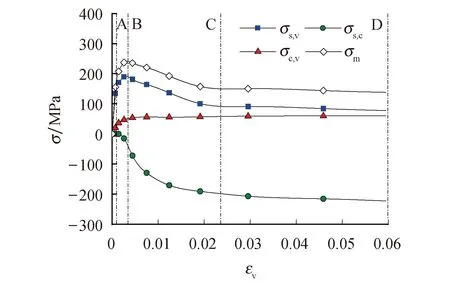
图5 典型构件各部件应力-应变发展Fig.5 Stress-strain relationships of each component part

2.2 应力分布

典型算例1/2高度处核心再生混凝土纵向应力(S33)分布情况如图6所示.考虑到荷载与构件几何对称性,仅给出了1/4截面的应力云图,各特征点处再生混凝土应力分布特征如下:

图6 1/2高度处核心再生混凝土纵向应力云图

1) 在A点处,再生混凝土处于弹性阶段,其纵向应力分布均匀且数值较小;

2) 在B点处,再生混凝土纵向应力较大且分布不均匀,由核心至边缘逐渐减小,这是由于再生混凝土截面中心处受到的约束效应较强,此时核心处纵向应力是其自身抗压强度的1.76倍;

3) 在C点时,再生混凝土纵向应力较B点有所下降,应力分布规律仍表现为截面中心至边缘逐渐减小,与B点处应力分布规律一致;

4) 在D点处,应力分布规律整体不变,再生混凝土纵向应力进一步减小.

2.3 接触分析

图7为典型算例中不锈钢管与再生混凝土接触应力(p)沿柱高的变化规律.如图所示,在初始加载阶段,沿柱高各点不锈钢管与再生混凝土接触应力均为零,表明此阶段不锈钢管与核心再生混凝土之间无接触作用,这主要是由于此阶段再生混凝土处于弹性阶段,混凝土泊松比小于钢材泊松比;随着再生混凝土横向变形增大,其泊松比开始增大并超过钢材泊松比,两者开始产生接触作用,并且随着构件纵向应变增加持续增长;当钢材进入塑性阶段后,B点与C点接触应力增长缓慢.

图7 不锈钢-再生混凝土接触应力Fig.7 Contact stress between steel tube and core concrete

3 参数分析

根据实际工程要求,在验证有限元模型可靠性的基础上,对102个RA-CFSST轴压短柱进行参数分析,其中设计变量考虑了取代率(r)、含钢率(α)、再生混凝土强度(fcu)、不锈钢管屈服强度(σ0.2)与截面尺寸(D)的影响.各参数取值如表2所示.

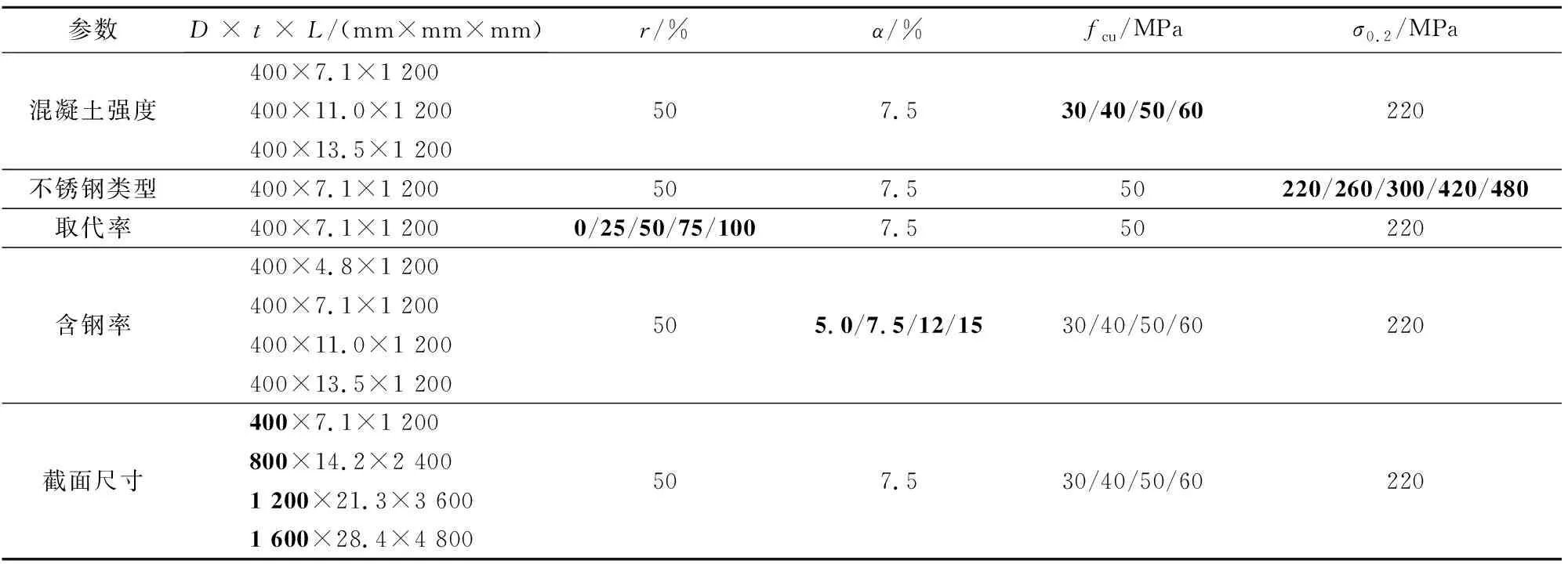
表2 参数分析算例

3.1 再生混凝土强度

图8a为在不同再生混凝土强度对构件荷载-位移(N-Δ)曲线与弹性刚度(EA)的影响规律.由图可知,随再生混凝土强度的增加,RAC-FSST构件极限承载能力Nu逐渐增加.尽管套箍系数ξ随着混凝土强度增大有所降低,但再生混凝土强度的增大仍有效提升了构件承载能力.这主要是由于混凝土强度的提高增大了核心再生混凝土部分的承载能力,抵消了套箍系数减弱对Nu的不利影响,导致构件的极限承载力在强度增大、套箍系数减小的情况下依然有所增加.本文有限元分析中,对于荷载-位移曲线没有明显下降段的试件,极限承载力Nu取为构件轴向应变1%对应的荷载[9],0.4Nu处的割线模量作为试件的轴压刚度EA[9,18].

图8b为不同再生混凝土强度对构件刚度的影响.可知,构件刚度随着核心再生混凝土强度的增加而增加,当再生混凝土强度从30 MPa增加至50 MPa时,构件刚度增加了12.9%.

3.2 再生粗骨料取代率

图8 再生混凝土强度的影响Fig.8 Effect of RAC strength

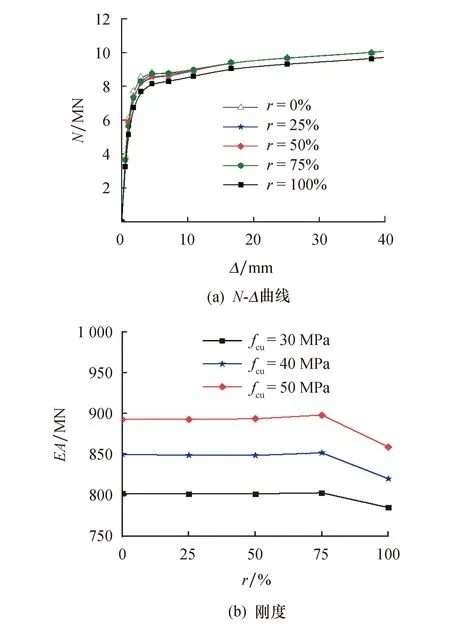
图9 再生粗骨料取代率的影响Fig.9 Effect of coarse recycled aggregate replacement ratio

3.3 不锈钢类型

不同不锈钢类型(包括奥氏体(X2CrNi19-11、X2CrNiMoN17-11-2与X2CrNiN23-4)、双相型(X2CrNiN23-4与X2CrNiMo22-5-3)以及铁素体(X8Cr17))力学性能如表3所列.

表3 各类型不锈钢的力学性能

图10为不同不锈钢类型对RA-CFSST短柱轴压性能的影响.有限元模型中,不锈钢类型通过改变屈服强度、极限强度与硬化指数实现.由图10a可知,不锈钢类型对构件N-Δ曲线影响显著.不同牌号的奥氏体不锈钢管再生混凝土N-Δ曲线发展趋势一致,承载力在塑性强化阶段稳定发展,随后缓慢增加.σ0.2=300 MPa对应的奥氏体不锈钢极限承载力为σ0.2=220 MPa的1.12倍;双相型不锈钢管再生混凝土N-Δ曲线发展趋势在弹性阶段与奥氏体不锈钢一致,塑性阶段荷载增长率大于奥氏体不锈钢,从弹塑性阶段开始曲线持续上升;铁素体不锈钢σ0.2=260 MPa,其N-Δ曲线发展趋势与奥氏体相似,极限承载力较奥氏体不锈钢σ0.2=220 MPa提高6.2%,较奥氏体不锈钢σ0.2=300 MPa降低4.9%;双相型不锈钢σ0.2=480 MPa极限承载力为奥氏体不锈钢σ0.2=220 MPa的1.4倍.从图10b中可知,构件刚度随着不锈钢屈服强度的增大而增大.

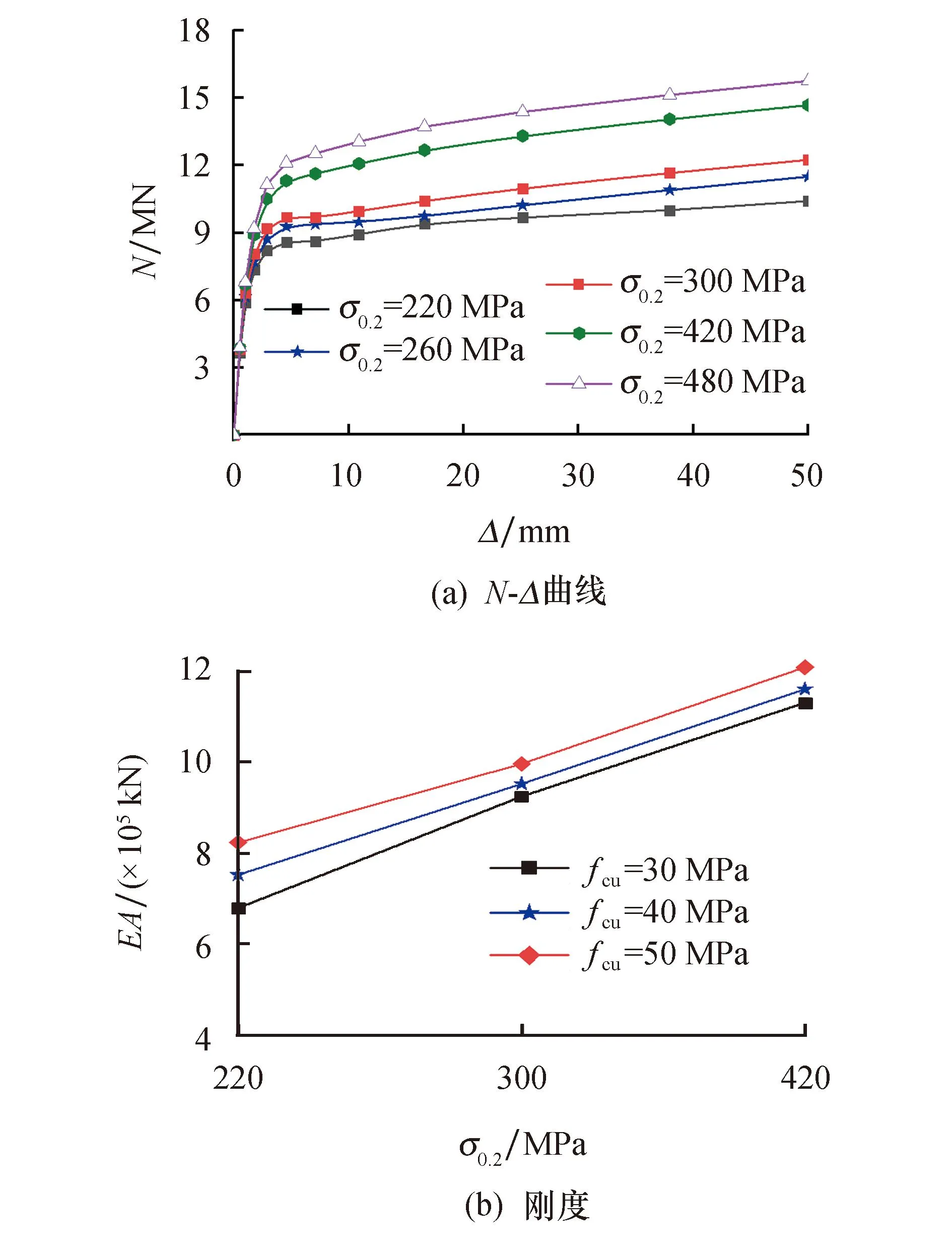
图10 不锈钢类型的影响Fig.10 Effect of stainless steel types

3.4 含钢率

工程中钢管混凝土的常用含钢率为4%～20%,本文通过改变不锈钢管厚度实现含钢率的变化.图11给出了不同含钢率下不锈钢管再生混凝土柱的极限承载力和刚度的变化.构件的极限承载力与含钢率成正比.当再生混凝土强度为30 MPa时,含钢率从7.5%增大到12.0%,其极限承载力增加幅度为11.5%;由图11b可知,构件刚度随着含钢率的增大而增大.可见,通过改变钢管厚度增加含钢率,可以增大构件的极限承载力和刚度.这是由于含钢率较大的试件,外包不锈钢管对核心再生混凝土的约束效应较强,核心再生混凝土强度提升幅度增加,进而增大了构件的极限承载力和刚度.

3.5 截面尺寸

为研究截面尺寸对不锈钢管再生混凝土短柱轴压力学性能的影响,本文设计了400、800、1 200、1 600 mm四种直径的试件.图12给出了不同截面尺寸下不锈钢管再生混凝土柱的极限承载力和刚度的变化规律.由图可知,随着截面直径的增大,试件的极限承载力和刚度均逐渐增大.

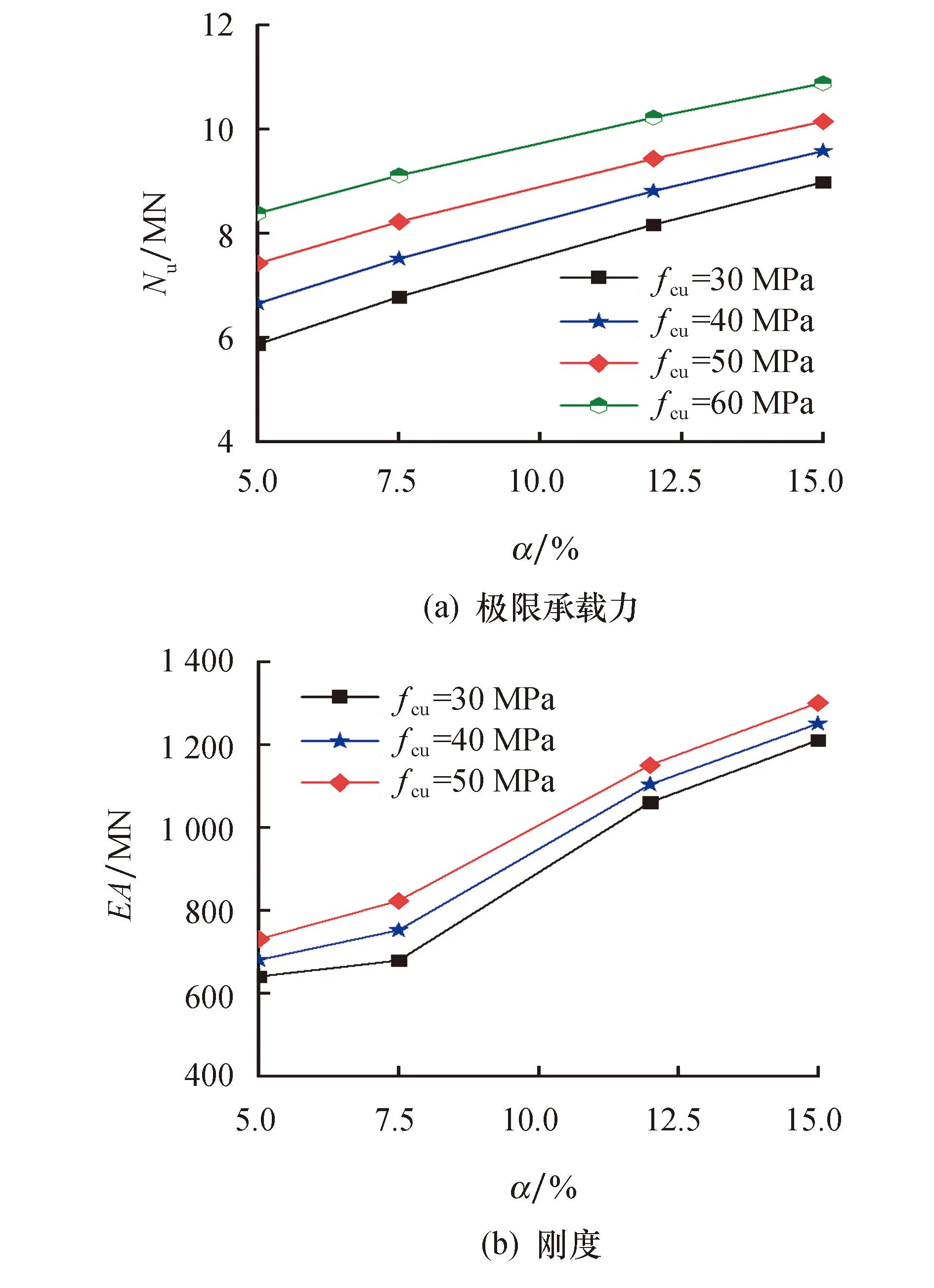
图11 含钢率的影响Fig.11 Effect of steel ratio

图12 截面尺寸的影响

4 轴压极限承载力计算

由于暂未出台RA-CFSST构件的相关设计规范,因此本节采用钢管混凝土结构设计相关设计规范EN1994-1-1:2004[19]、AIJ 2008[20]、GB 50936-2014[21]、ANSI/AISC 360-16[22]以及T/CECS 625-2019[23]预测RAC-FSST构件的极限承载力.为进一步验证现有规范对RA-CFSST构件极限承载力预测的适用性,本文将有限元模拟结果及相关文献试验结果[2,3,5,7-9]Nue&FE与规范预测结果Nuc进行对比分析.

在本文研究参数范围内,图13给出各设计规范预测值Nuc与有限元模拟结果、试验结果Nue&FE的对比.算例参数范围为:再生粗骨料取代率r=0%～100%、含钢率α=5%～15%、混凝土强度fcu=30～60 MPa、不锈钢屈服强度σ0.2=220～480 MPa和截面直径D=400～1 600 mm.可以发现,5种设计规范对RA-CFSST柱的轴压承载力预测均较为保守.欧洲规范EN1994-1-1:2004[19]和中国钢管混凝土结构技术规范GB 50936—2014[21]预测相对合理,计算结果与试验结果相比分别低估了8.8%和17.0%.而日本规范AIJ 2008[20]和美国规范ANSI/AISC 360-16[22]由于未考虑约束作用影响,对RAC-FSST极限承载力的预测偏于保守,极限承载力分别被低估了21.9%和26.0%.

图13 现有设计规范适用性对比Fig.13 Comparison of test and FE results with available design codes

5 结论

基于相关试验研究,本文对不锈钢管再生混凝土短柱轴压作用下的工作机理与影响参数进行了分析,在研究参数范围内得到以下结论:

1) RA-CFSST构件截面应力发展可分为4个阶段.构件在弹性阶段处于单向受压状态,不锈钢管与再生混凝土无相互作用;弹塑性阶段后不锈钢管环向应力持续增加,对再生混凝土的约束作用不断增强,再生混凝土纵向应力逐渐增大并趋于稳定发展,不锈钢管与再生混凝土接触应力持续增加.

2) RA-CFSST短柱极限承载力受再生粗骨料取代率的影响较小,取代率从0%增加到100%仅降低构件极限承载力6.2%;受含钢率和材料强度的影响较大;再生混凝土强度对构件刚度的影响不明显.含钢率从7.5%增大到12.0%,再生混凝土强度为30 MPa的构件极限承载力增加了11.5%,这主要与钢管对核心混凝土的约束效应增强有关.

3) 国内外现有钢管混凝土结构设计规范普遍对RAC-FSST构件极限承载力预测较为保守.其中,欧洲规范EN1994-1-1:2004和中国钢管混凝土结构技术规范GB 50936—2014可较好预测RA-CFSST构件的极限承载力.