基于短行程特征聚类的移动源排放清单构建方法

李兵兵, 康 宇, 曹 洋, 李亚民, 许镇义

(1.安徽省生态环境监测中心,安徽 合肥 230071; 2.合肥综合性国家科学中心人工智能研究院,安徽 合肥 230088; 3.中国科学技术大学 自动化系,安徽 合肥 230026; 4.中国科学技术大学 先进技术研究院,安徽 合肥 230088)

0 引 言

近年来,随着我国城市化进程和社会经济的快速发展,机动车保有量快速增长,移动源排放会造成细颗粒物和光化学烟雾污染,已成为我国城市大气污染重要来源。排放清单作为移动源污染定量核算的重要手段,可以用于大气污染防治措施制定与溯源分析。

车辆行驶工况是针对某一类车辆,在特定区域和时间段下,描述该类车辆行驶规律的速度-时间曲线。随着车速增加,燃油车细颗粒物排放物质量浓度会明显升高,在车辆加速情况下,车辆排放的颗粒物数量、质量浓度也明显增高[1]。通过研究道路移动源行驶工况来估计车辆排放,对移动源排放清单构建具有重要参考价值。

美国和欧洲开展汽车排放标准研究较早,已建立符合其交通特点与行驶状态的行驶工况,如新标欧洲循环测试(New European Driving Cycle,NEDC)工况[2]、美国联邦试验规程75(Federal Test Procedure 75,FTP-75)工况[3]。NEDC工况测试时间较短,速度分布比较规则,行驶里程较短且加速度比较稳定,其循环时长为1 180 s,行驶里程为11.007 km,平均速度为33.6 km/h,主要在欧洲、中国、澳大利亚等国家和地区使用。FTP-75工况是美国环境保护署用于排放标准制定的测试工况,其由车辆冷启动阶段、车辆热稳定阶段和车辆热启动阶段3部分组成,工况总时长为1 874 s,行驶里程为17.77 km,平均速度为34.1 km/h,主要使用的国家和地区包括美国、加拿大、南美洲等。

随着城市路网规模不断扩大,车辆高速行驶时间不断增加,欧美和日本排放实验领域专家共同制定了全球统一的轻型车测试工况(Worldwide harmonized Light-duty vehicle Test Cycle,WLTC)[4]。WLTC工况主要包括低速阶段、中速阶段、高速阶段和额外高速阶段,工况运行时长为1 800 s,运行距离为23.3 km,平均速度为46.3 km/h,其充分考虑车辆性能差异,对不同功率质量比的车辆采用不同测试循环,能够客观真实地反映车辆的实际排放状况。

当前行驶工况合成方法主要包括基于马尔科夫决策的工况构建方法和基于聚类算法的短行程构建方法。

文献[5]基于马尔科夫决策方法,使用特定的选取原则进行片段选取,形成聚类片段库,从而从物理意义上反映车辆的行驶规律;该方法适用范围广泛,不限道路类型,但在起始和终止片段的选取方面缺乏统一的选取原则。而起始和终止片段的选取,特别是起始片段的选取,将直接影响所构建工况模型的精确性。

文献[6]首次提出基于聚类算法的短行程构建方法,该方法可以有效地与主成分分析(principal component analysis,PCA)[7]和K-means[8]等聚类方法相结合,自动选取行程片段,因此受到更多的关注。

在国内,文献[9]针对不同测试循环工况下的轻型车污染物排放特性进行研究。

由于我国汽车工业起步较晚,目前在工况测试排放标准研究方面大多沿用欧洲的NEDC工况,但是该工况与我国目前的人员驾驶习惯及车辆标准有一定出入。因此,根据我国实际道路驾驶数据,构建符合当地实际路况的行驶工况具有现实意义,对于车辆排放物及燃料消耗等测试与评价有重要参考作用。

同时,现有的移动源排放清单研究大多基于文献[10]中的排放因子本地化修正方法,采用欧洲环境署开发的宏观排放模型COPERT(Computer Program to calculate Emissions from Road Transport model)[11]、美国环境保护署应用于汽车排放源计算的IVE模型(International Vehicle Emissions Model)[12]和美国环境保护署开发的移动车辆排放模型(MOtor Vehicle Emission Simulator,MOVES)[13]等排放因子模型方法,初步探讨了全国[14]、区域[15-17]、省(直辖市)[18-21]、省会城市[22-23]等多个尺度的机动车污染物排放结构组成、时空分布特征及相应减排情景对策等。

本文采用基于PCA和K-means聚类的短行程法,构建福州市轻型车的行驶工况。首先对原始数据进行预处理、划分运动学片段并计算其特征参数,运用PCA对划分后片段进行参数降维,再对其进行K-means聚类分析形成典型片段库;然后分别根据最小参数偏差法和最大相关系数法挑选片段组成行驶工况,对比后输出最终工况,并对最终行驶工况进行有效性验证;最后利用VT-Micro(Virginia Tech microscopic)模型并结合合成工况,计算单车排放因子,构建2020年福州市机动车排放清单。

1 基于短行程特征工况的清单构建

本文提出一种基于短行程特征聚类的移动源行驶工况排放清单构建方法,具体步骤如下:

1) 对获取的车辆GPS轨迹数据进行预处理。

2) 对轨迹的速度数据进行片段划分得到运动学片段,并根据运动学片段特征计算车辆运动学特征参数和总数据的总体分布参数。

3) 利用PCA对运动学片段进行运动学特征参数降维。

4) 使用K-means聚类对输入片段进行分类,得到多种类型的片段库。

5) 分别按照最大相关系数法和最小参数偏差法从各类片段库中挑选输入片段,构建合成行驶工况,并对比2种方法所构建工况的综合指标。

6) 引入VT-Micro模型,计算合成工况排放清单。

1.1 数据采集

本文采用未规定路线的自主行驶法采集福州市出租车行驶数据。不限定出车时间及地点,将GPS定位的终端设备安装于实验车辆上,进行数据远程传输和存储。为使得采集的轻型车行驶数据可以代表福州市乘用车行驶特点,行驶路线涵盖福州市主要道路。

福州市区分为5个行政区,下辖5个县及2个县级市。5个行政区分别为鼓楼区、台江区、晋安区、仓山区及马尾区,前3个为福州市主城区。5个县包括闽侯县、闽清县、永泰县、罗源县及连江县,2个县级市为福清市、长乐市。福州市区道路网呈“棋盘式+环路”分布。

考虑到大部分车辆行驶轨迹都集中于二环以内,且大部分的医院、商场、学校等也设于二环内,本文选取的主要实验区域为鼓楼区、台江区、晋安区及仓山区;考虑到福州大学、闽江学院及马尾区也会占有城市部分交通量,选择二环快速、三环快速、福州绕城高速及主城区内的主干道作为实验主要线路。

利用车载自动诊断系统(On-Board Diagnostics,OBD)接口采集发动机运行状态信息,车辆运行参数包括轨迹点采样时间、GPS车速、X轴加速度、Y轴加速度、Z轴加速度、轨迹采样点经纬度位置坐标、发动机转速、扭矩百分比、瞬时油耗、油门踏板开度、空燃比、发动机负荷百分比和进气流量,累计采集331 550条GPS轨迹数据,采样时间间隔为1 s,车辆运行参数的4种统计数据见表1所列。

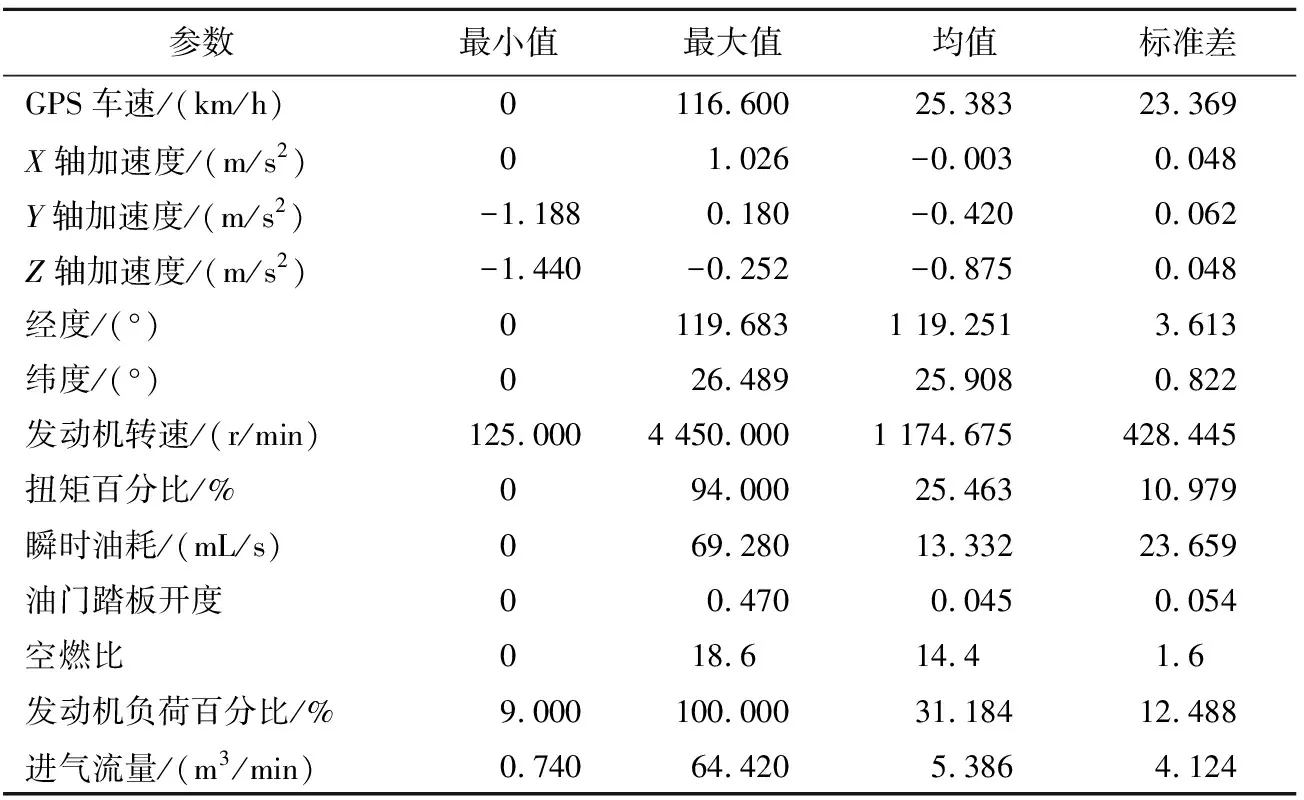
表1 车辆运行参数4种统计数据

1.2 数据预处理

需要对采集的原始GPS轨迹和车辆信息数据进行预处理,以去除无效片段及各类异常值,保证用于构建工况的行驶数据有效可靠。

考虑到轨迹数据采样时间间隔为1 s,车辆运行前后时刻速度不会突变过大,因此可以根据前后时刻的速度来填充当前时刻速度,若前后时刻速度全部缺失,直接删除该数据。速度缺失值处理策略见表2所列,插值处理结果如图1所示。

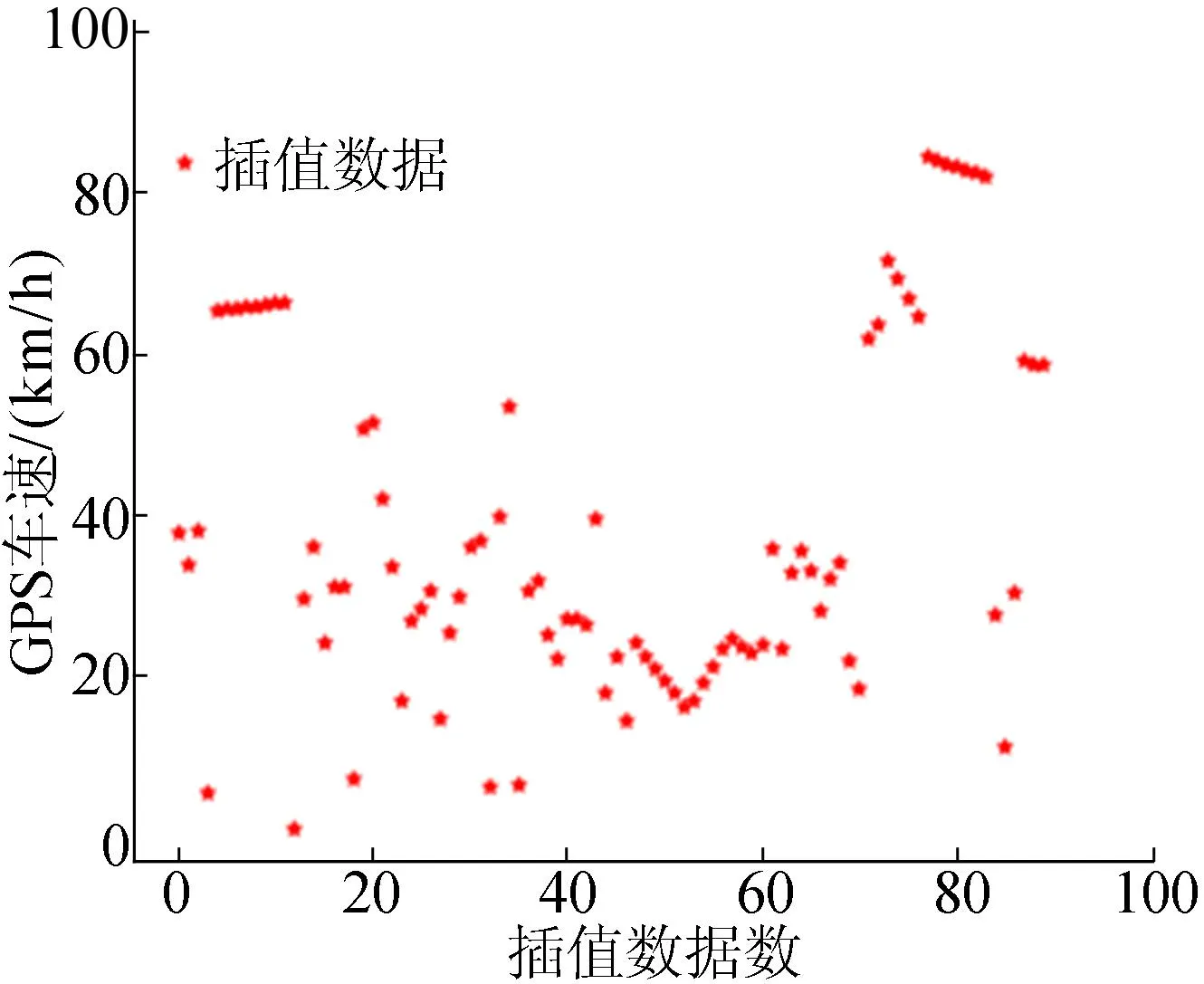
图1 GPS车速缺失记录插值处理结果

表2 速度缺失值处理策略

经车载设备直接采集的原始数据会包含部分异常数据。由于高层建筑或隧道遮挡,部分时刻GPS信号丢失,使得采集数据中的时间不连续,对于此类数据直接进行丢弃处理。若车辆长时间低速且间断行驶(速度小于10 km/h),则可视为怠速状态,默认最长怠速时间为180 s,多于180 s则按异常值进行丢弃。

1.3 运动学片段划分与特征参数计算

由于行驶过程中车辆速度随时间的变化特点不同,可以根据加速度和速度将不同类型的速度-时间片段定义为不同的运动状态,便于后续分析和聚类。本文定义以下4种运动状态:

1) 怠速状态。车速值为0但发动机转速值不为0的运动状态。

2) 加速状态。车辆加速度大于0.15 m/s2的运动状态。

3) 减速状态。车辆加速度小于-0.15 m/s2的运动状态。

4) 匀速状态。车辆加速度在-0.15～0.15 m/s2之间且车速值不为0的运动状态。

将运动学片段定义为前一个停车时刻(速度值降为0)到下一个停车时刻之间的速度-时间曲线,因此运动学片段会由1段速度值为0的怠速片段和1段速度值不为0的行驶片段组成。

由于从上一停车时刻到下一停车时刻,速度必须经过上升和下降过程,车辆必然会出现加速、减速、匀速等状态,运动学片段一般会出现怠速、加速、减速、匀速4种运动状态。典型运动学片段组成如图2所示。不同的运动学片段是车辆在不同地段不同时间段的行驶数据,其速度-时间曲线的时间长度及形状特点存在差异,而每个运动学片段都由若干个速度-时间点构成,通过定义各类特征值来区分不同曲线,也能定量刻画不同曲线之间的差异性,为后续的聚类分析提供依据。

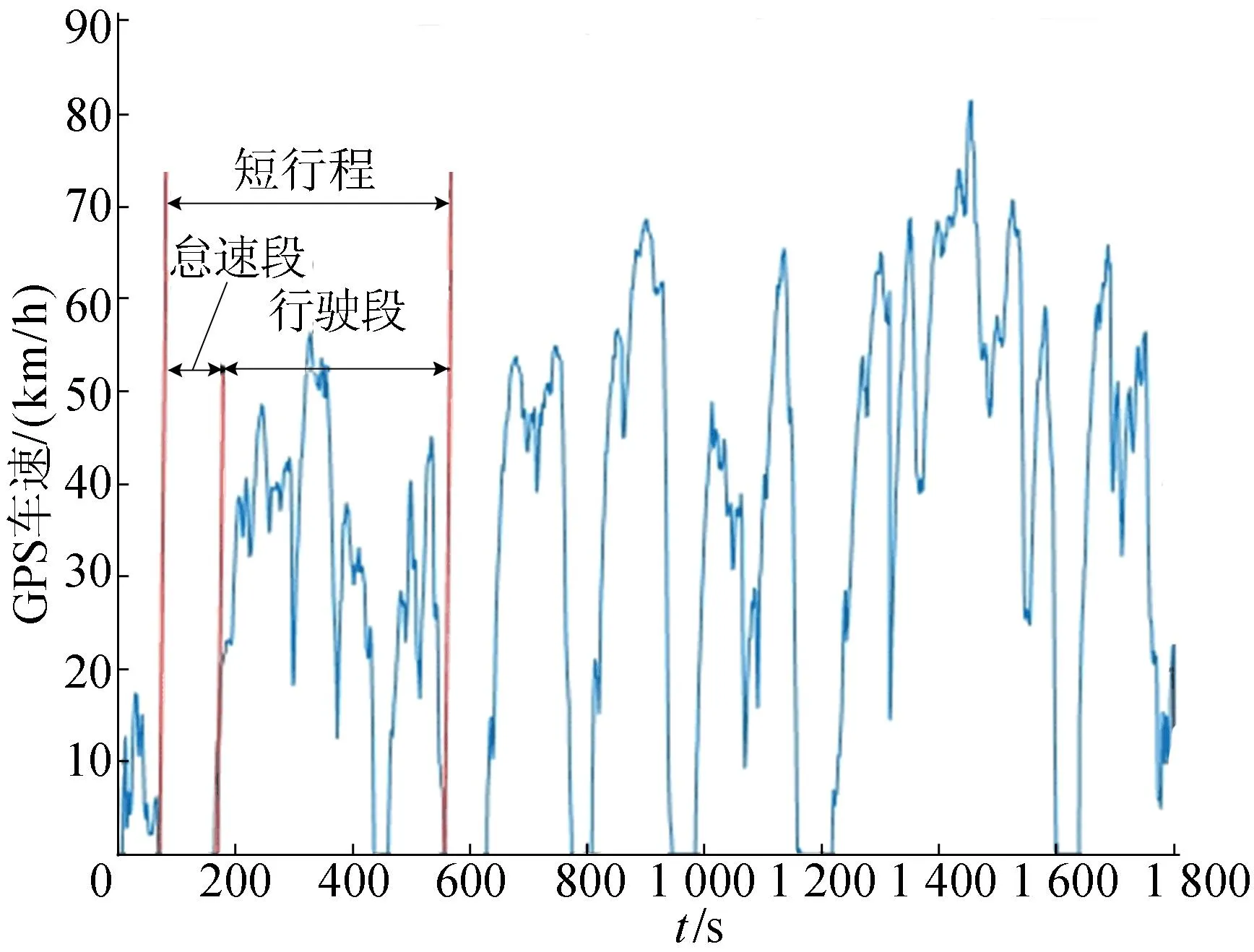
图2 车辆运动学片段组成

同时,在构建最终行驶工况后,还需要一些指标来定量分析和评价其有效性和准确性,以及与车辆真实行驶情况的贴近性。

因此,选取的特征参数必须尽可能全面、准确地描述运动学片段的运动特点。根据参数用途,将定义的特征参数分为2个大类:① 车辆运动特征参数,主要用来描述运动学片段的运动特征,可作为后续聚类分析的分类依据;② 数据总体分布特征参数,主要用于最终构建工况的检验与有效性验证。选取的15个车辆运动特征参数和10个数据总体分布特征参数分别见表3、表4所列。

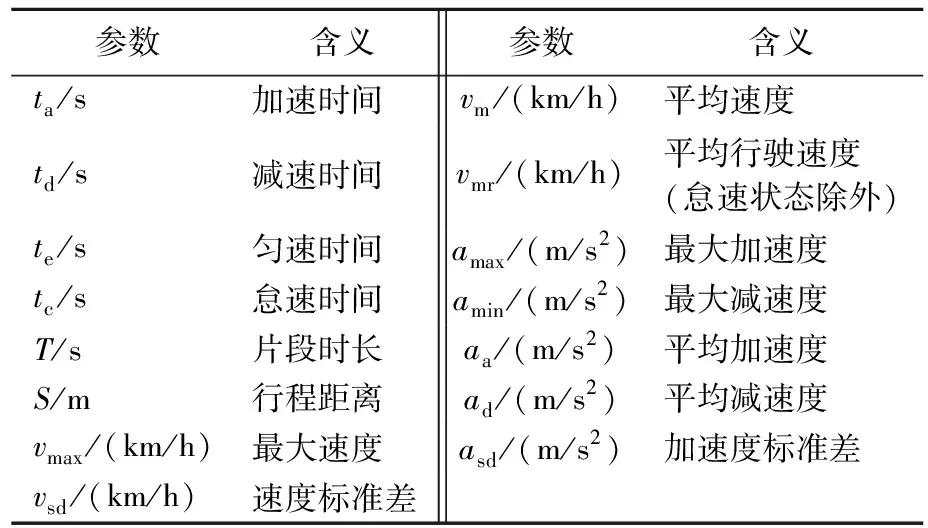
表3 车辆运动特征参数及其含义

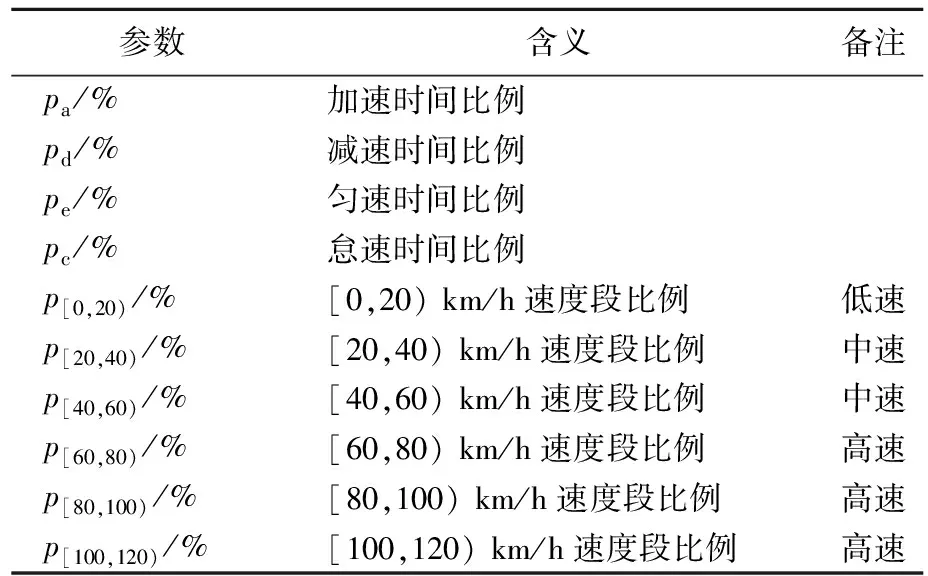
表4 数据总体分布特征参数及其含义

首先对加速度特征参数进行计算,在采样数据中,陀螺仪加速度是无法直接使用的,需要根据速度数据单独计算车辆加速度,即

(1)

其中:Δt为采样时间间隔,Δt=1 s;vt+1、vt分别为t+1、t时刻速度;at+1为t时刻到t+1时刻的加速度。

其次计算各类行程时长特征,计算公式为:

T=N

(2)

ta=Na

(3)

td=Nd

(4)

tc=Nc

(5)

te=N-Na-Nd-Nc

(6)

其中:N为运动学片段的总点数,考虑数据采样时间间隔为1 s,采样点数等于运动时长;Na为加速度大于0.15 m/s2的总点数;Nd为加速度小于-0.15 m/s2的总点数;Nc为速度为0的总点数。

然后依次计算S、vmax、vm、vmr、vsd、amax、amin、aa、ad及asd,计算公式分别为:

(7)

vmax=max{v1,v2,…,vN}

(8)

(9)

(10)

amax=max{a1,a2,…,aN}

(11)

amin=min{a1,a2,…,aN}

(12)

aa=

(13)

ad=

(14)

(15)

将所有采样样本按照式(1)～式(15)进行参数计算,得到2 818个运动学片段的车辆运动特征参数和样本的总体分布特征参数。

4种运动状态时间占比分别为:

加速,25.02%;减速,20.35%;

匀速,30.43%;怠速,24.19%。

速度分布占比分别为:

p[0,20),43.35%;p[20,40),26.43%;

p[40,60),18.99%;p[60,80),6.49%;

p[80,100),4.10%;p[100,120),0.60%。

由运动状态分布结果可知,福州市轻型车的加速、减速、匀速和怠速4类状态时间分布较为均匀,其中匀速时间段比例最大(占比30.4%),由此可见福州市轻型车的行驶较平稳,匀速驾驶状态占比较大。而根据速度分布结果可知,大部分时间车辆速度处于[0,40) km/h的中低速区间,高速([60,120) km/h)占比小(占比11.2%),具有较强的区域特征。因此,构建特定区域或时间段行驶工况对于车辆行驶特征研究是必要的。

在聚类后,会生成K个(K为聚类类别数)不同的典型片段库,在进行片段挑选构成最终工况时,需要计算能代表典型片段库的综合参数,以反映该片段库的车辆行驶特点。基于一定挑选原则,根据每个片段车辆运动学参数和典型片段库整体参数的接近程度,来挑选构成最终工况的运动学片段,采用相关系数法挑选片段时需要片段综合参数。本文选取pa、pd、pc、pe、vmax、vm、vmr、amax、amin、p[0,20)、p[20,40)、p[40,60)、p[60,80)共13个指标作为片段库的综合参数。考虑到速度段[80,120) km/h的数据占比不足8%,纳入综合指标会导致较大偏差,因此,保证[0,80) km/h区间的速度分布贴合,即可保证构建工况的准确性。将典型片段库中每种状态时间总和除以典型片段库的总运行时间得到各类状态占比。

1.4 基于PCA和K-means的典型工况构建

短行程法将不同运动学片段根据特征参数值相似度分为几类,形成能反映不同交通特点和行驶状况的典型运动学工况片段库,再根据一定的原则从库中挑选出片段组合,形成最终的工况曲线。本文先通过PCA将冗余参数去除,只留下几个主要特征组合,再通过运动学片段聚类构建典型工况片段。

利用PCA对运动学片段进行运动学特征参数降维,样本数据包含m个个体、n个评价指标,则相应指标矩阵为:

(16)

重新组合成的新综合指标为:

(17)

在新的综合指标中,Fi、Fj为不相关特征向量。方差达到最大并要求其依次递减,满足的限制条件为:

(18)

在进行PCA之前,需对各类指标进行标准化处理,消除单位影响。标准化计算公式为:

(19)

(20)

(21)

则标准化后的矩阵为:

X=[X1X2…Xp]

(22)

相关系数矩阵为:

(23)

其中,rij为Xi与Xj的相关系数。rij计算公式为:

(24)

(25)

计算出相关系数矩阵的特征值λ及特征向量E,则有:

|R-λE|=0

(26)

主成分贡献占比fi、主成分累计贡献率ak计算公式分别为:

(27)

当ak>85%时,主成分可以代表绝大部分信息,主成分值可计算为:

Z=[Xu1Xu2…Xuk]=[Z1Z2…Zk]

(28)

其中,uk为对应的主成分特征向量。

1.5 基于合成工况的单车排放因子估算

(29)

其中:v为车辆的平均速度vm;Rv,j为车辆在vm下的第j种污染物排放因子;Ri,j为第i个比功率区间的第j种污染物排放率;Pi,v为vm在第i个比功率区间的分布值。

由于无法直接获取机动车污染物排放率数据,需要利用其瞬时速度和加速度数据进行估算。VT-Micro 模型能够基于车辆的瞬时速度和加速度计算车辆瞬时排放,其结构简单,被广泛用于交通研究中[24]。利用 VT-Micro模型进行交通排放测算,计算公式为:

(30)

其中:v为车辆的瞬时速度;a为车辆的瞬时加速度;Rv,a为车辆在v、a下的排放率;αi,j为vi和aj的回归系数,根据美国橡树岭国家实验室收集的车辆排放数据[24]得到的回归系数取值见表5所列。

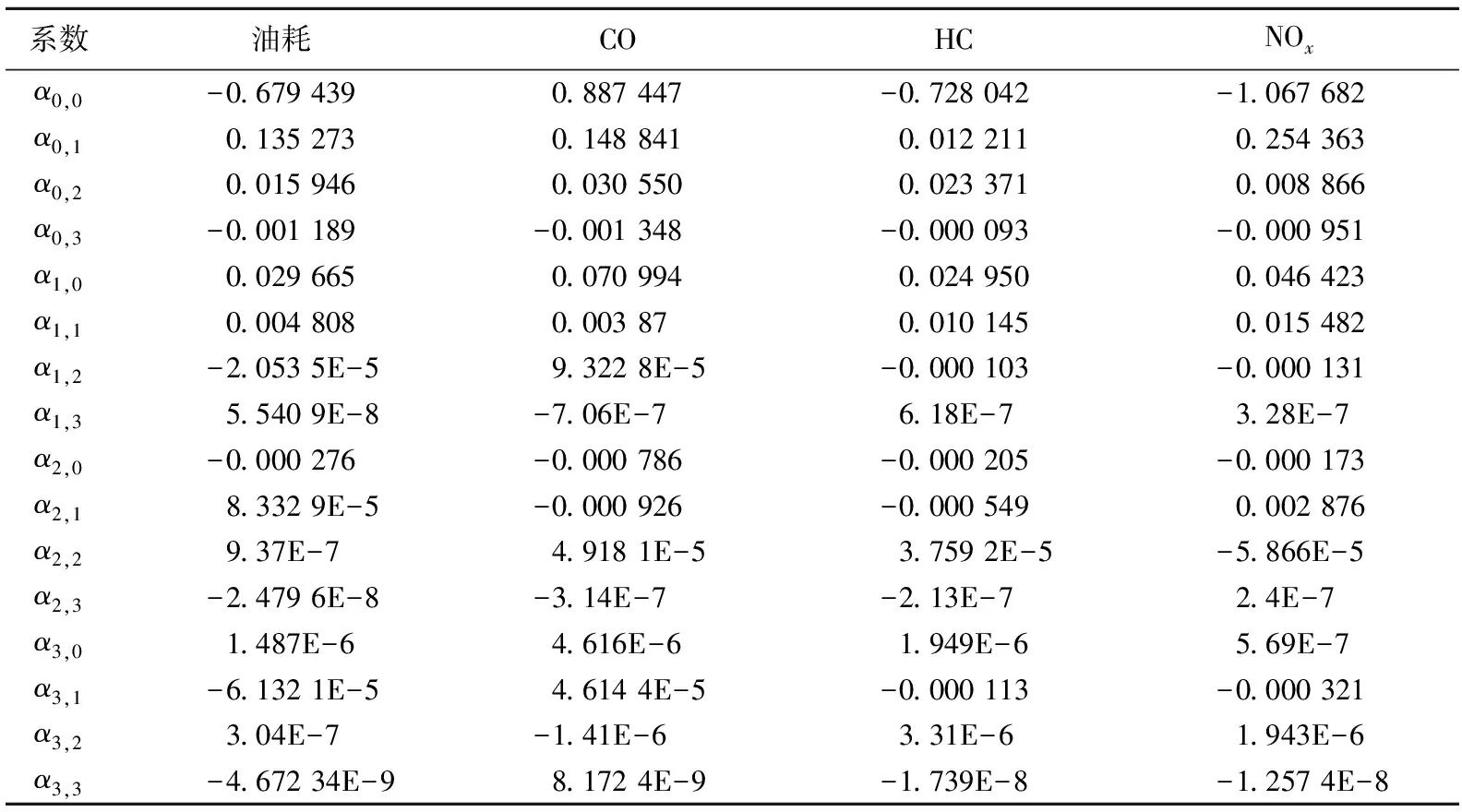
表5 回归系数αi,j取值

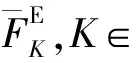
(31)

2 实验和讨论

对划分的运动学片段采用PCA进行分析,得到前4个主成分M1～M4,其累计贡献率为88.64%,大于85%,则前4个主成分可以代表样本的大部分信息。主成分方差及贡献率见表6所列,前4个主要成分的载荷矩阵见表7所列。

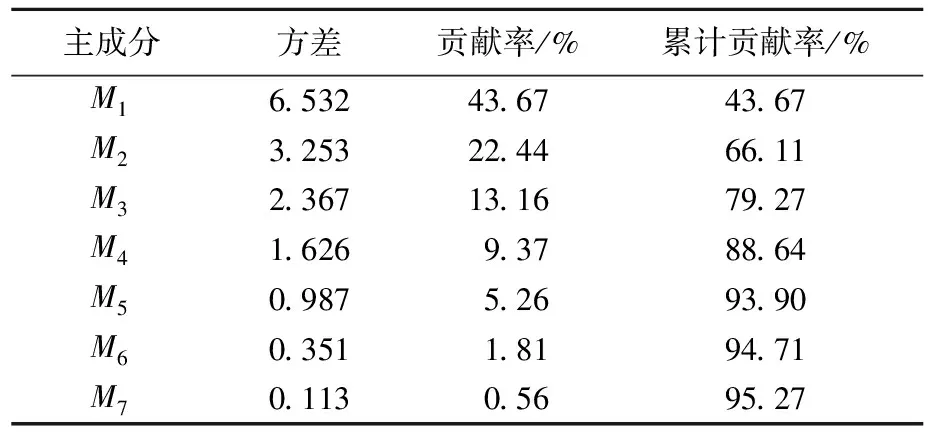
表6 车辆运动特征参数主成分方差、贡献率计算结果

表7 前4个主成分特征载荷矩阵

对划分的运动学片段进行K-means聚类,得到典型片段库,并根据戴维森-堡丁指数(Davies-Bouldin index,DBI)选择最优聚类数。DBI通过计算距离来度量相同类之间的相似性、不同类之间的差异性,计算公式为:

(32)

其中:k′为簇别数;avgCi为第i类样本点到簇中心ui的欧式距离平均值;dcen(ui,uj)为第i类簇中心ui与第j类簇中心uj之间的欧式距离。DBI越小,表示相同类运动学片段之间的相似性越高、不同类运动学片段之间的差异性越大,聚类效果越好。选取DBI值第1次出现局部最小值时的k′值,作为最优聚类数k0。根据最小参数偏差法和最大相关系数法,分别对各类片段进行排序挑选,计算各类片段库占总体片段库的时间比,确定各类片段库中选取的片段时长,根据排序优先级挑选片段形成行驶工况。最终选择聚类数目k′=3,聚类效果通过t分布随机邻近嵌入(t-distributed stochastic neighbor embedding,t-SNE)方法可视化,如图3所示。

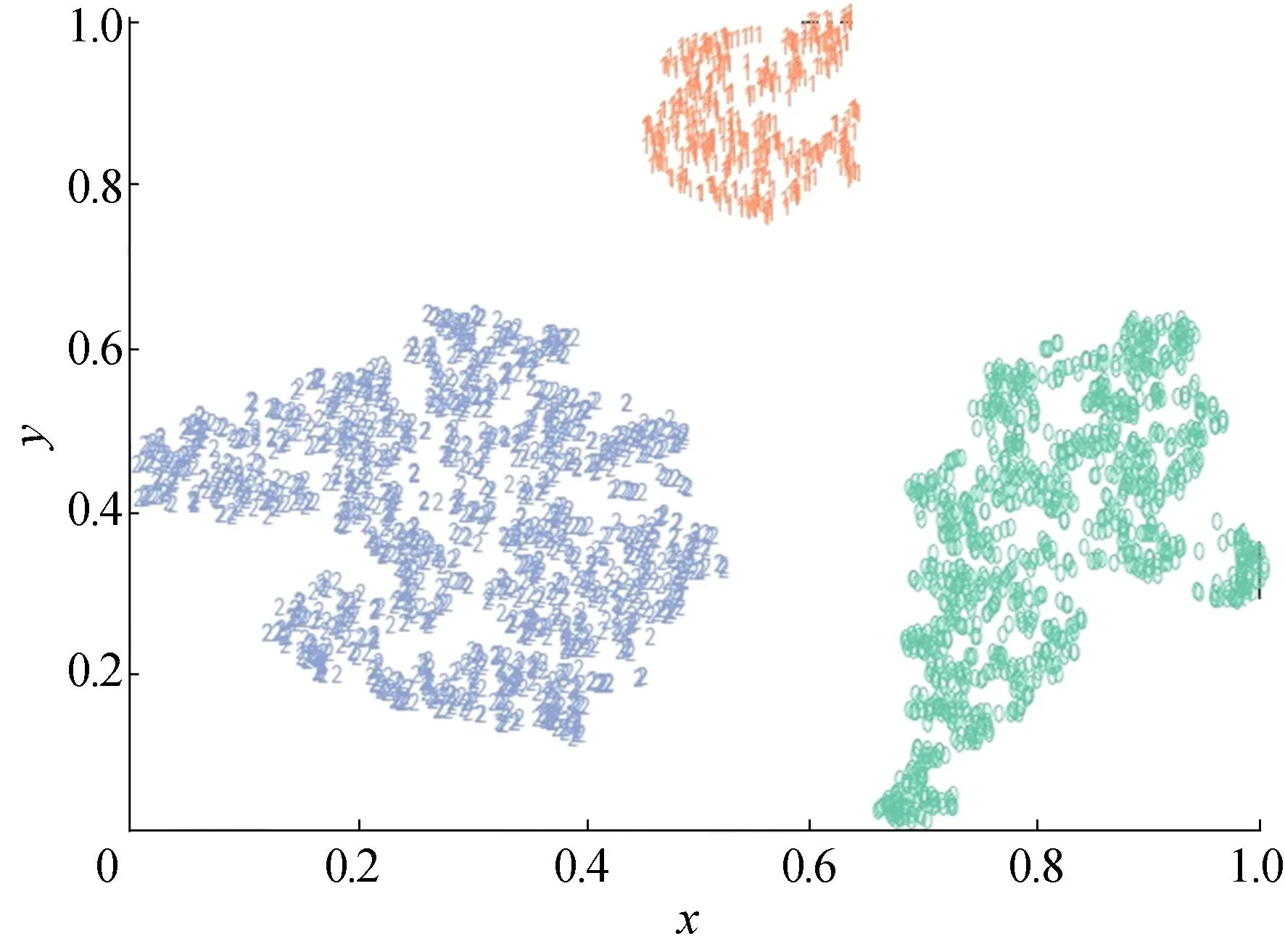
图3 运动学片段聚类t-SNE降维可视化

进一步分析各类库所代表的车辆行驶特征,根据参数整体分布情况,可将运动学片段分为低速(类别2)、中速(类别0)、高速(类别1)3类,计算典型运动学片段库综合参数,结果见表8所列。

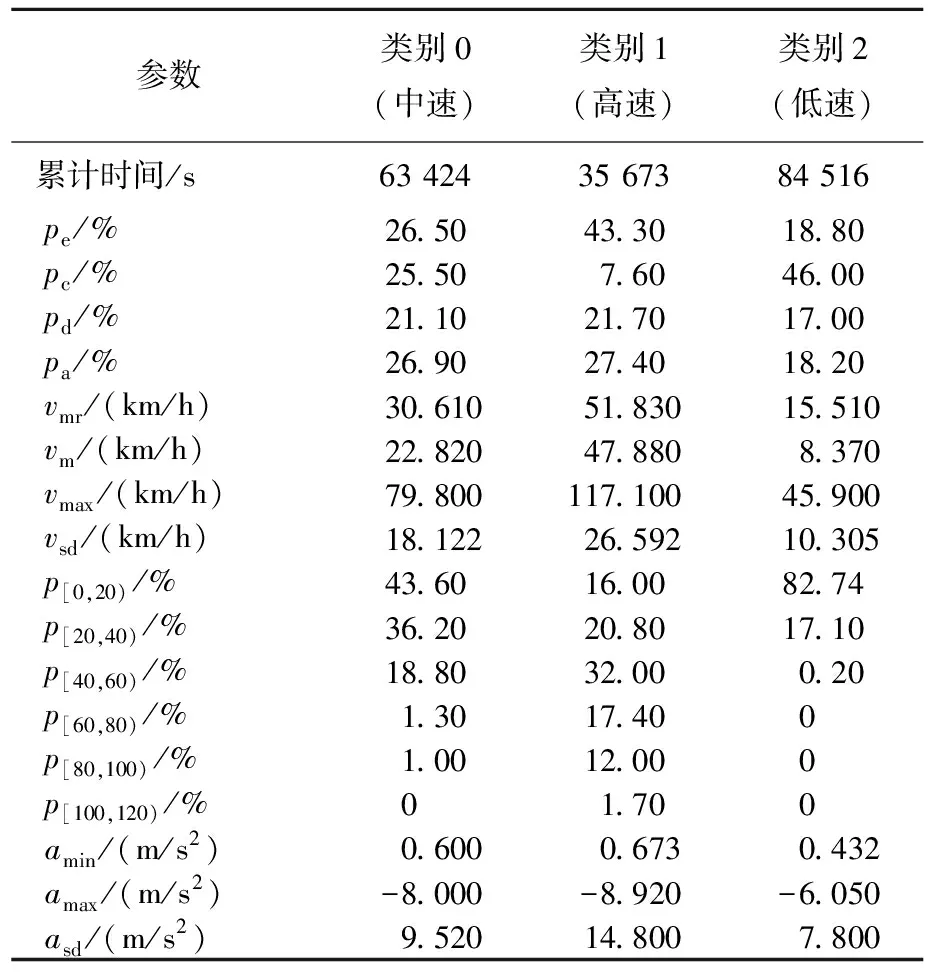
表8 3类典型片段库综合参数

类别1运动学片段匀速比例大,速度最大值高达117.100 km/h,且中高速([40,80) km/h)及高速([80,120) km/h)占比最大,可定义为高速行驶片段,且加减速时间均匀、匀速比例大,路况畅通,属于高速公路或快速道行驶。

类别2运动学片段低速占比(82.74%)非常大,怠速比例大,平均速度仅8.370 km/h,可定义为低速行驶片段,属于市内拥堵路段或低速次干道行驶。

类别0运动学片段以中低速([0,40) km/h)为主,4种运动状态时间均匀,平均行驶速度适中,最大速度介于类别1与类别2之间,为中速行驶类型,属于主干道行驶。低速行驶时长(84 516 s)占比最大,中速时长(63 424 s)占比次之,高速时长(35 673 s)占比最少,可见福州市乘用车整体以低速拥堵行驶情况为主,主干道行驶情况较少,高速公路及快速道行驶情况极少。

所有运动学片段被分为高速、中速、低速3类典型片段库。为客观反映车辆真实的驾驶特性,最终的工况应该涵盖这3类典型运动学片段,并且在最终工况中的各类片段时间比例与整体数据中比例一致。本文采用总体最大相关系数法(方法1)与最小参数偏差法(方法2)2种方法进行片段挑选,3类典型片段2种方法选择结果如图4～图6所示。

图4 高速片段2种方法选择结果

图5 低速片段2种方法选择结果

图6 中速片段2种方法片段选择结果

对于2种片段选择方法构建出的工况,用平均相对误差来检验工况的有效性。平均相对误差即所有参数相对误差的平均值。

2种片段选择方法所构建工况的相对误差见表9所列。

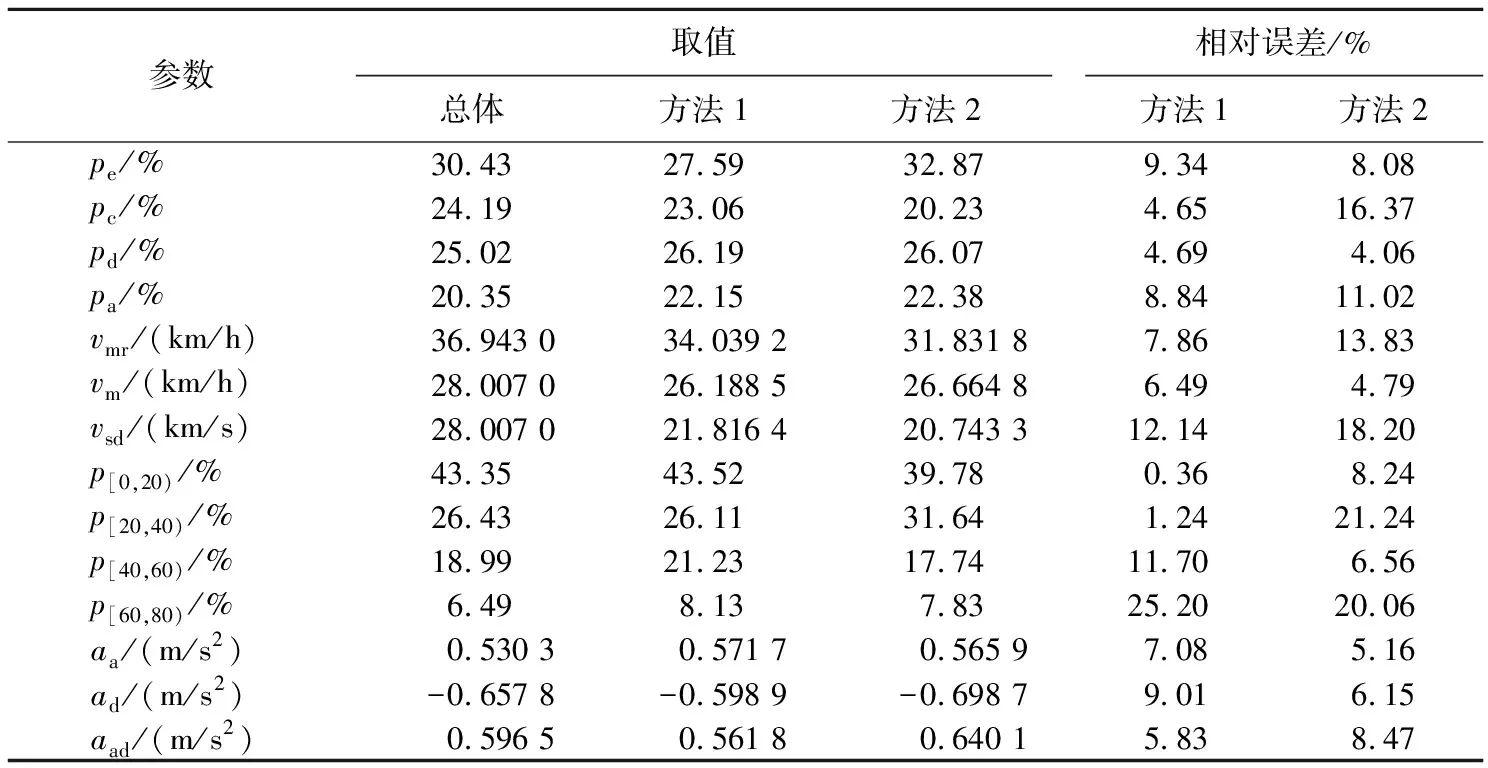
表9 2种方法片段合成相对误差

由表9可知:最大相关系数法(方法1)和最小参数偏差法(方法2)的平均相对误差分别为7.49%、10.88%,最大相关系数法的平均相对误差更小,其整体工况更贴近于真实驾驶情况;在运动状态占比和速度占比方面,最大相关系数法明显更加贴近总体数据。因此,选择最大相关系数法输出工况为最终工况。

最终构建的工况参数在整体上和真实行驶情况很贴近,尤其是在速度段[0,40) km/h比例与4种运动状态比例方面吻合度极高,在速度段[60,80) km/h和速度标准差方面吻合度欠佳。

根据式(31)计算出单车合成工况排放因子,见表10所列。

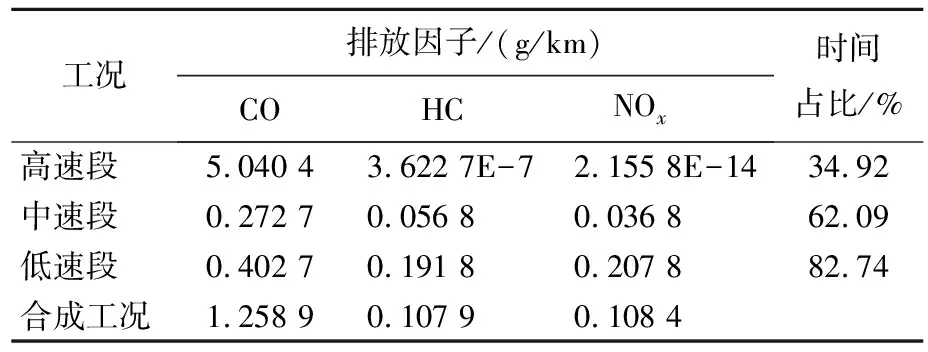
表10 单车合成工况排放因子计算结果

根据文献[25],2020年福州市汽车保有量为1 498 695辆,公路通车里程合计11 616.816 km,得到2020年福州市机动车污染物排放清单,见表11所列。

表11 2020年福州市机动车年均排放清单 单位:t

3 结 论

本文提出一种基于短行程特征聚类的移动源行驶工况排放清单构建方法,采用基于PCA和K-means聚类的短行程法,构建福州市轻型车的行驶工况。首先对原始数据进行预处理、划分运动学片段并计算其特征参数,运用PCA对划分后片段进行参数降维,再对其进行K-means聚类分析,形成典型片段库;然后分别根据最小参数偏差法和最大相关系数法挑选片段组成行驶工况,对比后输出最终工况,并对最终行驶工况进行有效性验证;最后利用VT-Micro 模型并结合合成工况,计算单车排放因子,构建2020年福州市机动车排放清单。主要结论如下:

1) 相比于传统的随机选择法,本文采用最大相关系数法和最小参数偏差法,分别以参数向量整体相似度最高和参数数值总体偏差最小为标准进行最终工况的片段挑选。

2) 对于选定参数作出较大调整,主要是以整体参数为准,去掉p[100,120)([100,120) km/h速度段占比不足1%,会引入较大误差)、vmax、amin等参数,目的是追求整体吻合度更高,大部分数据贴合真实情况,而不是追求极值或者少部分数据拟合效果。

3) 在实验线路及区域选取时,根据车流量分布特点,按一定比例选取主城区与郊区实验车辆;并采用“不选定路线的自主行驶法”采集行驶数据,驾驶员可不受限制地自主驾驶,采集数据更具真实性。

本文虽然考虑行驶工况信息进行排放清单构建,但采用的VT-Micro排放因子模型仍然是一种基于统计回归的数学估算模型,最终的排放清单核算与实际情况仍然存在较大偏差。在未来的研究中,可考虑利用便携式排放测试系统(portable emissions measurement system,PEMS)获取的实际道路排放监测数据,对现有排放因子估算模型进行修正,以获得较准确的排放清单核算。