基于信号分析技术的呼吸机工作状态自动化识别研究

张宝慧，陈艳林，訾聪娜，韩 伟，滕金亮，2

（1.河北北方学院附属第一医院，河北张家口 075000；2.河北医科大学，河北石家庄 050004）

呼吸机可以为重症患者进行机械通气[1-2]，以保证患者能够摄入足够的氧气，为抢救工作提供充足的时间。对呼吸机工作状态的识别能够保证紧急抢救工作顺利进行[3]，目前在该方面的研究较少。为了实现对呼吸机工作状态的识别，结合信号分析技术，通过小波变换对呼吸机工作状态进行识别，其主要通过管路内是否出现积液的信号特征进行识别[4-5]。

1 小波分析概述

1.1 小波变换的连续性

对于小波变换[6-8]的连续性表述，是基于空间L2(R)的可容许性条件。设空间中存在函数f(t)，将该函数在小波基下展开运算，对应的运算可以表示为：

式中，WTf(a,b)为小波变换对应的系数，ψ(t)为小波变换对应的母函数，a为小波基对应的尺度，b为平移因子。小波变换的连续性表现为其是一种连续变换。在小波变换中，针对某一信号，其连续变换等于各分量变换的总和。

1.2 小波变换的离散化

对呼吸机进行压力波数据的采集，其数字信号的采样频率为50 Hz[9]，小波变换后无法直接处理相应的数字信号，需要对小波变换进行离散，以便于更为直接地处理数字信号[10-11]。在对小波变换进行离散时，应先对小波基对应的尺度a进行离散。其中，当小波母函数ψ(t)满足式（2）中的条件时，可以得到基本的二进小波：

结合式（1），令尺度a=2k,k∈Z，可以推出二进小波的变换公式：

在将尺度a进行离散化之后，对平移因子进行离散处理。在对b进行离散处理时，设b=n·2k,k∈Z，由此得到小波变换离散后的函数：

1.3 小波变换的分解和重构

在对小波变换进行离散化之后，其整体为高通滤波器和低通滤波器结合的组成树。原始信号在高通和低通滤波器中分解后，得到一级分解信号。而后不再对细节信号（即高频分量）进行分解，而是继续分解近似信号（即低频分量）。依据信号分析时的特点，确定分解信号相应的级数[12-13]。

分解小波变换后得到相应的信号分量，将信号分量向原始信号进行还原，这一过程称为小波重构[14-15]。小波变换分解时，一般通过滤波和降采样来实现。在进行重构小波变换时，对应进行相应的滤波和升采样操作。对分解后的小波分量进行除噪过滤，过滤相应的噪声分量后进行重构，得到相应重构后的信号。

2 检测积液模型

2.1 工作状态判定

呼吸机[16]管路是否存有积液，通过对应的压力波形来进行判断。当波形中存在高频噪声时，管路中存有积液。呼吸机在正常工作状态和存有积液情况下压力波形如图1 所示。

结合图1，当呼吸机管路中存有积液时，可以观测到明显的高频噪声信号。

2.2 整体流程概述

对于呼吸机的工作状态，即其中是否存在积液的判定，以呼吸周期为基准做出设计。在一个呼吸周期中，积液可能发生在吸气管路或者是呼气管路，同时患者在进行呼气或者吸气时，产生的波形也有所区别。因此呼气相和吸气相不能进行统一的阈值设定。在进行工作状态检测时，需要对呼气相和吸气相进行区别判定。

首先进行呼/吸气相临界点检测。检测时定义呼吸波形正负时的过零点为对应的临界点；然后进行呼气相和吸气相分离；之后进行小波变换的分解、重构以及阈值选择的过程，由阈值进行积液判断，从而完成检测。

2.3 分解及重构呼吸波的小波变换

结合实际在管路中积液的特征以及小波变换理论对压力波形进行分析，小波基的阶数设定为五阶，由此对压力波形进行五层小波变换。

呼吸机正常状态和存在积液时，得到的近似信号a1以及细节信号d1-d5层如图2 所示。

图2 正常状态和存在积液时近似信号a1和细节信号d1-d5层

结合图2 可以观察到，在细节信号的d1-d3层，当管路中存在积液时，其高频信号相对明显。从信号分析来看，积液存在的信号特征表现在d1-d3层。

在对小波变换进行重构时，通过四种不同的方式进行信号重构。构造元素为d1-d3，获得重构信号S1、S2、S3、S4，其重构方式为S1=d1，S2=d1+d2，S3=d1+d2+d3，S4=(d1+d2+d3)K，其中，K为对应的构造变量，其取值在[0.05、0.1、0.5、1.0、2.0] 中选择。

2.4 呼吸波检测算法

得到重构信号之后，对其进行标准差和均值的求取，由标准差以及均值选取相应的阈值。标准差以及均值计算方法为：

式中，std 为对应的标准差，di为信号中对应的采样点，N为小波基的阶数，μ为对应的均值。在对管路中是否存在积液进行判定时，需要对多个呼吸波形进行检测和分析。其具体的判定流程如图3所示。

图3 积液判定流程图

阈值选定的具体方式如图4 所示。

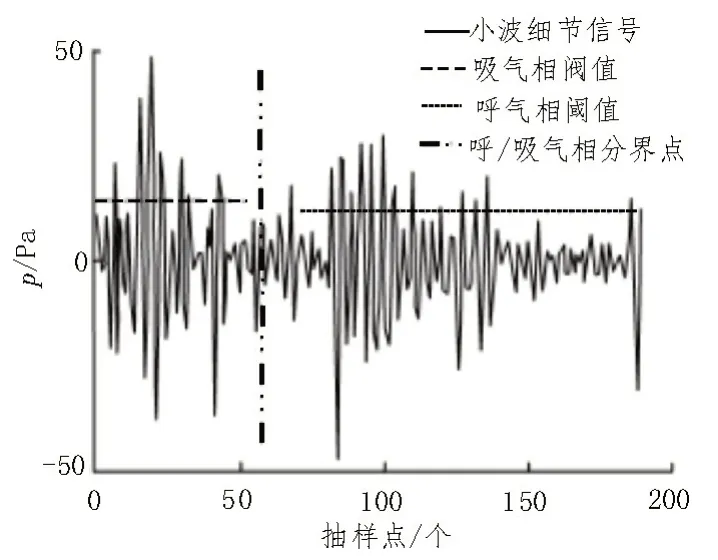
图4 阈值选定示意图

图4 中，呼气相与吸气相的阈值由于标准差以及均值的不同而不同。

2.5 测试用数据选取

通过临床采集患者数据以及模拟肺所产生的数据进行相应的积液检测测试。实验选取模拟数据的呼吸周期个数为163 个，测试所得104 例无积液，无积液用例中，为检验算法是否抗干扰，选用了人机对抗类型的呼吸波16 例，双触发类型的呼吸波74 例，常规的呼吸波16 例；59 例存在积液，存在积液用例中均为双相存在积液。临床数据采用某医院的心外科重症监护室，测试患者选择个数为3，包括呼吸周期个数为1 161。其中，管路中双向积液的测试用例为125，呼气相积液的测试用例为614，积液总个数为739例，正常无积液的个数为422，对应呼吸波均正常。

3 实验结果分析

测试实验采用五折交叉验证的方式进行，而后对灵敏度以及特异度进行均值求取，得到最终实验结果。

进行小波重构后积液检测后得到相应的感受性曲线。吸气相得到的感受性曲线如图5 所示。

图5 吸气相感受性曲线

在图5 的吸气相感受性曲线中，重构方式为S1时性能最优，为S4时性能相对最低。

呼气相得到的感受性曲线如图6 所示。

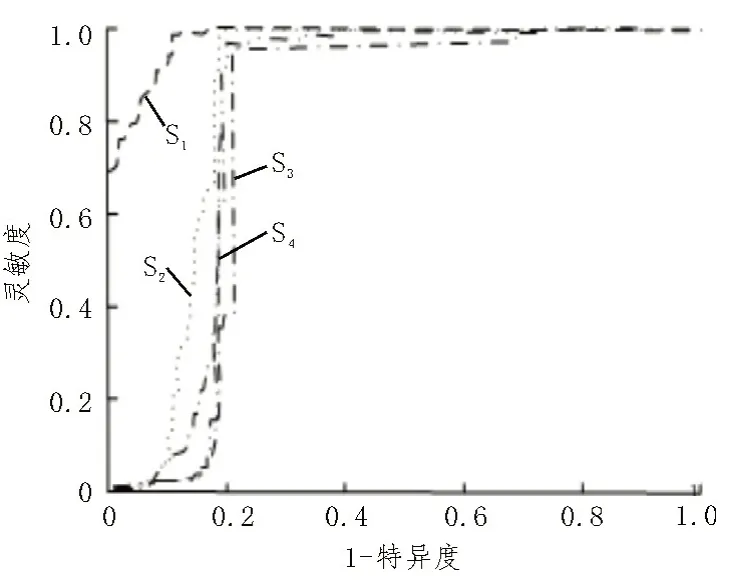
图6 呼气相感受性曲线

在图6 的呼气相感受性曲线中，重构方式为S1时最优，S2、S3、S4相对差别较小。

四种重构方式所得的感受性曲线下面积分别为呼气相0.978、0.854、0.810、0.809，吸气相0.989、0.855、0.810、0.809。由此可知，S1的重构方式与其他重构方式相比，在呼气相与吸气相均为最优。

同时针对模拟数据以及临床数据进行相应的测试验证，主要对比准确率、特异度以及灵敏度三个方面的内容。临床数据进行测验所得结果如表1所示。

表1 临床数据测量结果

表1 中，临床数据测试用例个数较多，整体上通过S1的重构方式所得到的判定性能在灵敏度以及准确度上均为最优。

模拟数据所得结果如表2 所示。

表2 模拟数据测量结果

表2 中，重构方式S1、S2以及S4对应灵敏度以及准确率的测量结果均一致，这是由于模拟用例较少。

综上，重构方式S1判定效果整体高于其他重构方式的原因是S1仅重构细节信号的d1层。其他重构方式由于对d2、d3层进行了重构，非积液的特征信号的数量增多，影响了阈值的准确设定，从而影响了测定的准确率。

4 结束语

通过小波变换，可对呼吸机管路内是否积液做出更加精确的判定，从而更加精准地识别呼吸机的工作状态。经过对临床数据以及模拟数据的验证，通过小波变换进行信号分析的方式切实可行。判定算法中，通过重构方式S1在临床数据以及模拟数据中均能实现较高的准确率。经验证表明文中方法具有很好的性能，但仍具有局限性，主要表现在实验数据量不多，对照单一。今后将进一步扩大样本范围，并尝试更多方式对呼吸机工作状态做出识别判定。