工程动态信号的精密测试与智能评估方法

沈 松， 刘进明， 鄢 明， 王治敏

（北京东方振动和噪声技术研究所 北京，100085）

引 言

动态测试技术主要用于对动态信号进行测试和分析，获取动态信号的频率、幅值及相位等特征参量。传统上动态信号分析仪主要是对音频范围内的动态信号进行测试分析，该频率范围通常在0~100 kHz 以内，常见的信号有地震、结构振动、动态应变、机械振动、转速、噪声和冲击等。动态信号测试不同于温度、压力等静态信号的精密测量，由于影响因素较多，一般较少讨论其测量的精密程度，当前使用的相关计量检定规程仅在5%~10%的精度［1］。随着工业技术的迅速发展，在诸如港珠澳大桥、绝对重力测量以及大量国防工程项目中，这样的精度已经无法满足需求。随着计算机技术和软件算法的发展，精密的动态信号测量技术已经成为现实。

对于一般的动态信号测量方法，传感器和模数转换（analog to digital conversion， 简称ADC）的精度是影响测试精度的首要关键因素。本研究在不考虑硬件精度的前提下，主要讨论通过测试技术和信号处理算法来实现精密测量的方法。实现动态信号的精密测量需要从系统进行考虑［2］，但是目前多数研究都集中在频率、幅值的校正上［3-14］，对阻尼的研究较少［15-20］，更鲜有考虑测试系统的整体动态系统特性。

对信号精密测量的最终目的还是用于信号识别和状态评估，不同于测量的精密化，评估则是相对“模糊”的。例如，传统上设定阈值判断设备运行健康状态的手段经常是不合理的。在传统机理研究与信号处理的基础上，结合人工智能方法进行识别与评估已经成为重要的研究方向，目前虽然已有大量相关文献，但都处于简单应用阶段，并且工程中的有效样本数量太少，这是阻碍其应用的一个重要问题。针对此问题，本研究分析总结了笔者在实际中已经成功应用的几种实用方法。

1 基本参量的精密计算

1.1 动态基本参量

一般动态系统可表示为

其中：a，b，c分别为微分项、线性项和积分项的系数，对于动力学系统分别对应加速度、速度和位移。

其运动为多个简谐运动的组合，每个简谐运动表示为

其中：A为振幅；n为阻尼系数，n=ξω，ξ为阻尼比；ω为圆频率，ω=2πf，f为频率；φ为初相位。

式（2）为某一个简谐运动的时间历程，其中的变量共同组成了动态系统的4 个基本参量。由式（2）可见，动态信号关心的并不是运动位移波形上的每一个数据点大小，而是反映动态特性的频率（周期特性）、振幅（幅度特性）、相位（时间差特性）及阻尼（运动衰减损耗特性）等指标量［2］。

1.2 无阻尼信号的频率、幅值和相位的精密计算

对于采样频率为fs的N点的动态信号波形x(n)，通常使用快速傅里叶变换（fast Fourier transform， 简称FFT）获得离散频谱曲线G(m)后，根据频谱中的谱峰获得多个频率成分的频率、幅值和相位。计算误差的根源来自于有限长样本的截断和频谱泄露，如图1 所示为一个单频正弦信号在离散频谱上由于FFT 频谱泄露导致的误差，正弦信号的频率为f，离散频谱的频率间隔为∆f=fs/N，记fk=k∆f。当f=(k+α)Δf，f∈(fk，fk+1)时，则会产生泄露误差［3］。

图1 FFT 频谱泄露导致的误差Fig.1 The error because of leakage of FFT spectrum

对于频率而言，读取谱峰位置的频率fk=k∆f，其最大误差为±0.5∆f；对于幅值而言，最大误差可达-36.2%［3］。加窗是最常用的幅值修正手段，例如hanning 窗可将幅值误差减小至-15.3%，平顶窗可将幅值误差减小至-1%以内，但是加窗的同时却更加模糊了频谱中的频率成分，相位的误差也会随之增加。以上是对信号中仅包含单个频率成分的分析，工程信号中常常包含多个频率成分，传统上使用细化快速傅里叶变换（zoom fast Fourier transform ，简称ZoomFFT）等分析方法，但是这些方法需要更多的数据来实现，所以并不适合实际工程中的应用。对于非密集频率的情况，目前主要通过两类途径，在不增加数据长度的条件下来获取精确的频率幅值等参量。

1.2.1 基于频谱校正的方法

利用频谱中真实信号频率两边的2 条或多条谱线进行内插或比值计算［4-7］，得到更加接近于真实信号的频率和幅值，以式（3）所示的能量重心法［8-9］为代表，该类方法计算简单，多用于频率校正，但是可修正的程度有限，并且对于不同的窗函数需要分别推导公式［3］。

1.2.2 基于离散傅里叶变换的方法

该方法利用离散傅里叶变换（discrete Fourier transform， 简称DFT）来消除FFT 的泄露误差，以FFT/FT 方法为代表［10-11］，首先，采用FFT 进行全景频谱计算，确定某个频率成分f∈[fk-1，fk]之后，在该范围内进行频率细化，假设细化倍数为Z，则细化后的频率间隔为∆f′=∆f/Z；其次，对如式（4）所示的细化后各点频率f1序列进行式（5）所示的DFT计算；最后，搜索其中幅值最大的频率点作为最终结果。

FFT/FT 方法可以获得任意精度的频率、幅值和相位结果，只需不断加大Z即可，而付出的代价就是计算量随之增加。但是实际上，对于频率f1序列的计算并不需要逐个计算，可以使用各种优化搜索方法，例如结合1.2.1 节的内插或比值方法就可以极大加快搜索进度，基于该思想的方法［12］可以达到实时计算的速度，对仿真数据的计算误差达到10-15量级，可应用于采集仪器硬件精度的提升［13］。

1.3 有阻尼信号的阻尼、频率和幅值的精密计算

阻尼的精密测量相对更加困难，首先应设计合理有效的测量方法，得到信号的时域衰减曲线或高频率分辨率的共振频谱曲线，再通过信号处理来提高阻尼比的计算精度。

1.3.1 时域方法

式（2）所示的有阻尼单自由度自由振动响应曲线是一个振幅按指数曲线衰减的正弦信号，因此定义 的 阻 尼 系 数n、阻尼比ξ和 对 数 衰 减 率δ计 算［14］如下

其中：Ak，Ak+1为相邻波峰和波谷的幅值。

如果设计一个试验能获得结构自由衰减的响应曲线，就可以直接按照式（6）进行阻尼的计算。较为有效的试验方法为自然松弛法，该方法预先对结构施加静力，使结构处于某一阶弯曲振型的变形状态，然后突然释放，则结构将按该阶振型进行自由衰减运动，测量响应的波形并读取相邻谱峰的幅值即可准确计算出该阶振动的阻尼系数。

在实际工程测量中，自然松弛后的自由振动常常夹带有其他阶的微弱振动而导致测量误差。针对此，文献［15］分析了两自由度系统的自由衰减参数，文献［16］采用Laplace 小波分解等方法，而更加实用的方法则如式（7）所示

该方法通过Hilbert 变换计算信号的包络线曲线E(t)，然后按照指数衰减函数Ae-nt进行拟合，得到准确的阻尼系数n，使用包络线拟合计算的阻尼如图2 所示。

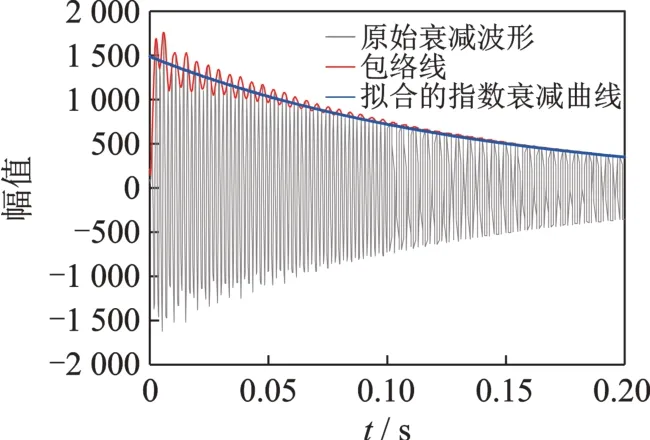
图2 使用包络线拟合计算的阻尼Fig.2 Damping calculate by envelop fitting

1.3.2 频域方法

时域法虽然简单可靠，但其试验方法常常难以实现，工程中更多使用半功率带宽法。利用功率谱中 某 个 共 振 峰 的 半 功 率 带 宽 直 接 按ξ=(f2-f1)/2f计算阻尼比［17］，其中f1和f2为半功率频率点。

使用半功率带宽法，离散频谱的频率分辨率∆f可能会对计算误差产生明显的影响，对于低频小阻尼情形，∆f相对较大，则可能产生百分之几百的误差［18］。使用INV 阻尼计方法［18］复原的精确频谱如图3 所示，建议在计算之后利用式（8）所示的准则，根据数据计算点数N判断是否能够保证计算精度［19］。

图3 使用INV 阻尼计方法复原的精确频谱Fig.3 Recover precise spectrum by INV damping meter method

当有条件设计共振扫频试验时，应通过共振峰附近的慢扫频试验获取较高频率分辨率的频谱，以提高阻尼比的计算精度，否则只能通过信号处理的方法来实现。文献［19］提出的ZOOMBDFT 方法是利用FFT/FT 的思想，文献［20］则采用对不同时间偏移位置分别进行FFT 计算来获取幅值衰减率，进而计算阻尼比。两种方法均获得较好的结果，但在计算过程中都未充分考虑衰减曲线的DFT 计算误差，并且细化倍数和偏移时间的选择也会直接影响计算精度。

基于功率谱精确计算阻尼比的INV 阻尼计方法［21］是通过推导出式（2）的响应在离散功率谱的各条谱线上的幅值，然后通过谱峰附近若干条谱线的测试数据进行拟合，直接获取阻尼、频率等结果。如图1 中 令α=(f-fk)Δf，ε=n/Δf，有ω=2π(k+α)Δf，则式（2）表示的时间历程曲线经过采样频率fs的离散采样后的N点时间序列可写为

该时间序列在离散功率谱的第k条谱线上的幅值可以通过傅里叶级数进行计算

将式（9）代入式（10）后经过推导和简化，可以得到第k条及附近若干条谱线的功率谱幅值公式为

读取实测功率谱在k点附近若干点的幅值，利用式（11）进行拟合计算，即可获得ε，α和A，从而计算精确的阻尼比、频率和幅值。INV 阻尼计方法使用简单、计算快捷，而且符合阻尼衰减振动的模型，因而可以获得很高的精度［18］。当得到阻尼比之后，利用式（11）令m为任意的小数，则可以反推出精确的频谱曲线。例如图3 为使用INV 阻尼计方法复原的精确频谱，其使用10.24 kHz 采样频率对信号200×e-0.01×202.5×2πtcos (202.5×2πt) 采 集1 024 点波形，图中显示了FFT 频谱和利用式（11）反推的精确频谱的差异，使用这两个频谱计算的阻尼比误差分别为123.7%和0.5%。

阻尼测量还有很多种情况，其中有两种比较重要的特殊情形：①对于无法自支撑的材料需要按《GB/T 18258—2000 阻尼材料阻尼性能测试方法》标准，将其附加在金属片上进行共振扫频试验再进行换算；②对于地基基础等阻尼比大于20%以上的情形，可以利用阻尼频率在振动加速度和速度之间的显著差异进行双峰法计算［22］。对于土木建筑类的大型复杂结构，其任何一点振动响应的阻尼比都不能代表整体振动阻尼，需要通过对结构模态测试和拟合计算才能获得较为准确的频率和阻尼［23］。几种常用频谱校正方法的比较如表1 所示，其中：“√”表示可用；“—”表示不可用。

表1 几种常用频谱校正方法的比较Tab.1 Comparison of several popular correction methods

2 系统动态特性的扩展与改善

除了硬件精度和算法误差外，测试系统的动态特性也是影响测量精度的重要方面。系统动态性能主要依靠相关芯片和硬件电路的性能指标，其中动态范围、频响性能及微积分转换等特性还可以通过测试方法和算法来进行改进和提高。

2.1 系统频响特性的畸变反演和范围扩展

动态信号测试系统尤其是传感器都具有一定的可用频响范围，超出此频率范围的信号也可能被测量，但是幅值和相位将产生畸变。图4 为一种国内普遍应用的941 型振动传感器频响曲线。图5 为列车经过桥梁时，使用不同传感器测量的动挠度信号，其中：实际曲线为位移计测量的结果，接近于真实曲线；测量曲线为振动传感器测量的结果，由于在低频的幅值和相位变化而产生了严重的畸变。

图4 传感器频响曲线Fig.4 The frequency response of a sensor

图5 桥梁动挠度信号测量结果Fig.5 Measurement signal of bridge dynamic deflection

传函反演［24］是能有效完成信号畸变实时修正的方法，可以扩展系统的可用频率范围。测试系统的频响特性为频率的传递函数Ha(f)，物理信号x(t)经过该系统后得到了产生幅值和相位畸变的离散数字序列̂(n)，此时可以再设计一个传递函数为Hd(f)=1/Ha(f)的数字系统，͂(n)经过该数字系统即可得到复原的信号x(n)，实现畸变校正的目的。

传函反演的实现方法如图6 所示，首先，对模拟系统（主要是传感器）的Ha(f)进行精确标定；其次，使用无限脉冲响应法（infinite impulse response 简称IIR）、窗函数等方法设计具有Hd(f)传递特性的数字系统［25］，让ADC 之后的数据经过该数字系统，即可获得反演后的真实信号波形。

图6 传函反演的实现方法Fig.6 Implementation of transfer function reversion

当传感器对某个频率范围的信号衰减到输出小于本身噪声水平时，或者对某个频率范围的信号达到共振时，该频率范围的Ha(f)实际上是无法标定的，也就无法实现反演。

2.2 微积分转换的全程计算方法

在振动测量中，有加速度、速度和位移3 个基本形式，三者之间的关系为微积分关系，工程中经常需要在这3 种形式之间相互转换。基于梯形法或辛普森法等的传统微积分运算方法，在对长时间的连续振动信号进行微积分计算时，具有难以克服的缺点。其中：积分操作易受信号基线和低频漂移的影响，导致积分后波形基线的大幅波动；微分操作易受信号局部噪声的影响，导致微分后波形噪声放大。对于二次微积分计算，则波动更加严重，实际工程中一般都加设高通或低通模拟滤波，但是这样一方面会丢掉被滤波的信号，另一方面滤波后波形存在非线性相位的畸变。

全程加速度-速度-位移变换（acceleration elocity displacement，简称AVD）方法采用了与传函反演类似的思路，设计一个具有微积分频响特性的数字信号系统即可，如式（11）中Hj(f)为一次积分的频响函数，Hw(f)为一次微分的频响函数，A(f)为幅频特性，P(f)为相频特性。同样的，可以类似写出二次微积分的频响函数，即

图7 为某跨海大桥的振动加速度实测波形，时间长度大约为40 s。图8 为梯形法和全程法积分后的速度波形，显然梯形法的结果具有非常强的低频振荡，是不真实的。该方法还应用于港珠澳大桥的隧道沉管姿态监测和对接，该项目需要在海底使用高精度加速度传感器经过2 次积分获取沉管的位移时间历程。常规的高通滤波后积分方法存在以下问题而无法使用：①高通滤波会丢失低频成分；②IIR滤波器的非线性相位特点导致实际波形产生变化。因此，基于全程算法的积分是最终实现2.5 mm 对接误差的水下沉管姿态监测部分的关键技术之一。

2.3 基于双核采集的动态范围提升

动态测试系统的动态范围是一个非常重要的指标，体现了幅值方面的测量能力，可反映在一次测量下（量程不变的情况下）同时可测幅值最大信号和最小信号的比，即在保证信号中大幅度变化的测量量程时，对叠加在其上面的微弱幅度变化的测量能力。其中，可测最大信号受量程的限制，而可测最小信号受本底噪声的影响，因此ADC 的位数是决定动态范围的首要因素。一般在设计动态测量仪器时，对每路信号的采集都直接使用一个ADC 转换器的输出结果作为采集后的数字信号，因此在单一量程下的可测量范围总低于ADC 的理论动态范围。

基于双核采集仪的设计思想则突破了这种惯性思维，该方法对每路信号的采集同时使用2 个24 位ADC 转换器进行转换，并在硬件中通过数字信号处理器（digital signal processing，简称DSP）或现场可编程门阵列（field programmable gate array，简称FPGA）对其进行重新组合［26-27］，其实现框图如图9 所示。一般24 位ADC 测试仪器的动态范围在110~130 dB，而采用双核采集的测试仪器的动态范围则可以达到160 dB，理论上在同一量程下可以同时满足幅度变化达108倍的不同信号的测量。

图9 双核24 位ADC 采集的实现框图Fig.9 Data acquisition by dual 24 bit ADC

3 基于测试系统建模的精密测量方法

前面讨论的不论是基本参量还是动态特性，都是针对单一环节的方法。如果测试系统比较复杂，则需要分析系统各个环节的误差，建立包含物理运动和测试误差的综合系统模型。由于对不同的测量目标搭建的测试系统各异，本节以绝对重力测量为例，讨论基于综合系统建模的精密测量方法。

绝对重力测量是指在地球某个点位进行重力加速度的精密测量，通常使用的重力加速度为9.8 m/s2，但 是 若 要 达 到μGal 级 的 精 度（1 μGal=10-8m/s2），需要考虑各种精密测量的方法。激光干涉测量是一种常用的方法，其原理是让一个物体在真空管作自由落体运动，在下落过程中测量各个位置的时间ti和位移zi，按照自由落体运动公式进行拟合计算，得到重力加速度a为

测量系统使用铷原子钟作为时间基准得到时间ti，使用激光干涉法得到位移zi，最终重力加速度a的误差大约为mGal 的量级。若要进一步提高到μGal 量级，则需要建立整个测量系统的模型来替代式（13）。

本研究基于中国计量院的NIM-3A 型绝对重力仪，建立的绝对重力测量的微振校正示意图见图10。首先，完善物理运动方程，进一步考虑重力的梯度差异，梯度表现在自由落体公式的3 次和4 次项中，增加重力梯度项的自由下落物理模型为

图10 绝对重力测量的微振校正示意图Fig.10 Microvibration correction for absolute gravimeter

其中：γ为梯度系数。

其次，考虑电路系统的干扰，主要存在激光调制频率ωr和市电工频ωs的干扰。ωr可根据激光系统的参数获得，ωs一般为50 或60 Hz。这两部分均为简谐分量，即

然后，继续考虑真空管筒体的前若干阶自振运动［28］，如前3 阶结构振动项为

其中：ωm为筒体结构的第m阶固有频率

最后，进行大地微振的补偿，相比于前3 项而言，对测量误差影响最大的则是来自大地微振引起反射镜的运动［29］，大地微振属于随机振动，不能进行直接计算，而需要通过精密振动测试系统来实时测量。采用双核160 dB 采集、传感器传函反演以及全程AVD 积分后，实现了纳米级大地微振的测量精度。将测量的大地微振di加入式（13）中，得到综合系统模型为

此外，还进行了环境大气压、地球潮汐和极移等影响的误差修正，最终使得测量的不确定度下降到10 μGal以下。图11为2017年的绝对重力测量的国际比对结果［30］，其中NIM-3A 的实测结果与各国仪器平均值相差仅为1.5 μGal，合成不确定度为5.8 μGal。

图11 绝对重力测量的国际比对结果Fig.11 International comparison results of absolute gravimeteries

可见，基于系统建模的精密测量方法从测量原理入手，综合考虑被测对象的物理特性、测量系统误差、辅助结构影响及环境干扰等因素，结合动态信号的精密计算方法，可获取非常高的测量精度。

4 基于特征提取与深度学习的动态信号识别与评估

动态信号的测量可以不断地精密化，但是对信号的识别与评估却需要智能化。通过对设备产生的振动与噪声进行机理研究，形成了很多用于信号识别和健康评估的方法。随着各类设备复杂程度的不断提高，仅仅通过机理特征去识别的难度越来越大。伴随着深度学习技术的快速发展，人工智能已经成为信号识别与评估的重要手段，但在工程动态测试领域，却面临着有效样本极少的困难，表现在以下两个方面：①大量的工程数据不具备规范统一的特点，并且由于测试方法和算法的不足而导致数据中丢失大量的原始信息；②机器故障的偶发特性导致准确标识的故障样本更少。因此，利用机理研究成果，对信号进行预先的特征化后再进入神经网络，可以有效减少神经网络训练对数据量的需求，但要避免过度信号特征化，防止丢失信号内部不易发现的潜在特征。

4.1 两种常用的特征化方法

4.1.1 基于信号特征量的机器学习

对于结构组成简单、故障形式明确的设备，为有效识别其早期和并发故障，可以对信号进行全面的特征量提取。初期无需考虑这些特征量的有效性，在积累一定量的数据之后对其进行降维处理，保留这些特征量中的主成分，最后将降维后的数据进行标准化，并选择一种聚类算法完成机器学习。

以某燃气热水器的下线检测为例，首先，热水器的常见故障表现于风机、电磁阀和燃烧室爆燃等，在生产线上对热水器的振动噪声进行在线检测，并从中提取了120 余种特征量，包括整机不同方位的声压和声品质、风机各阶次振动和噪声、电磁阀开合过程的各种波形统计量以及燃烧相关频率区段的频谱值等；其次，通过相关性或者正交性分析来完成降维处理，降维后保留了7 个特征量；最后，选择K-means 算法，随机取2 个中心点，并选取大致等量的合格与不合格样本进行训练，得到最终的学习模型，即可用于生产线中不合格品的在线识别。

4.1.2 基于谱阵彩图的深度学习

更多的信号难以简单地进行若干个特征量的提取，更好的方法是利用深度学习技术［31］。目前，较为成熟的卷积神经网络（convolutional neural network，简称CNN）已经在二维图像处理中得到广泛应用，因此利用信号的谱阵生成彩色图像非常适合于CNN 处 理［32］。2 种 适 合CNN 计 算 的 常 用 谱 图 如图12 所示。图12（a）为飞机经过测量仪器上方时测量的随时间变化的频谱谱阵图，可以看出有两类特征：①发动机频率由于多普勒效应而随时间持续减小；②空气噪声随时间变化由高到低再到高。对于旋转机械设备的故障识别，一般使用图12（b）所示的随转速变化的转速-阶次谱阵［33］。

图12 2 种适合CNN 计算的谱图Fig.12 Two spectrum maps for CNN calculation

4.2 少样本的解决办法

4.2.1 样本增强和迁移学习

样本增强实际上就是人为生成更多的样本数据提供给神经网络进行训练，简单的方法是通过计算机程序按照故障机理，叠加一些其他特征和噪声，生成大量的仿真故障数据。另外，还可以利用现有的样本数据，将每一个样本信号分离为故障特征部分和背景噪声部分，再重新进行交叉组合，产生更多的故障样本［34］。

迁移学习［35］是利用公有的训练模型，加入到私有模型中以提高私有模型的准确率，相当于应用了公有模型中样本数据的训练效果。一种基于机理信号分析、样本增强和迁移学习等深度学习的设备在线监测与健康评估流程如图13 所示。

图13 一种基于深度学习的设备在线监测与健康评估流程图Fig.13 A procedure of equipment online monitor and evaluation based on deep learning

4.2.2 自编码学习

当完全没有故障样本时，例如运行中设备一直未发生故障，只能收集到正常数据样本，此时需要使用无监督学习的方法建立推理模型。在4.1.1 节机器学习情形下使用的K-means 就是数据无监督学习的聚类方法，而对于4.1.2 节深度学习中则需要使用自编码神经网络模型，其特点是让神经网络的输出等同于输入，训练出的模型隐藏层中包含了编码和解码两部分，即对输入样本数据进行编码再解码后得到的输出等同于输入。该模型用于设备健康的实时监测中，若设备处于正常运行状态则测量数据输入给自编码神经网络后可输出原数据，一旦设备发生异常则测量数据输入后不能输出原数据，从而可判断是否发生异常。

5 结束语

本研究主要面向工程振动和噪声测试，在不考虑硬件芯片和电路精度的前提下，从计算算法和测试方法方面研究了基本参量的精密计算，讨论了影响动态系统的一些动态特性，并从工程实用性角度探讨了包含基本参量、动态特性和系统建模等方法。随着硬件仪器的精度提高和信号处理新算法的出现，动态测试进一步向更高精度发展。深度学习技术的发展为动态信号的智能评估提供了可能，针对无标签样本的无监督学习模型将成为人工智能的下一个发展重点，如2017 年提出的Transformer 编码器模型已经在语言理解项目GPT4［36］中取得了巨大成功。随着人工智能相关技术在工程应用上的深入研究，将解决无负样本的自学习等问题。