《问题解决能力量表（中文版）》本土适用性研究*

张亚杰 闫青青 肖茹梦

（1 河南大学教育学部，河南开封，475004）（2 河南省学前教育研究中心，河南开封，475004）

问题解决能力是个人运用认知技能来面对并解决真实的、跨学科情境的问题的能力。在问题情境中，解决问题的办法并不是一目了然的，可能用到的知识和技巧也不局限于数学、科学或阅读等某个单一领域。问题解决能力是个体应当具备的一项基本能力，〔1〕对个体的元认知能力、团队协作能力、沟通能力、创造性思维能力的发展均有显著正向影响，是高阶思维的核心能力之一，〔2〕也是深度学习的核心能力之一。随着时代的不断发展，国内外学者对问题解决能力越来越关注。已有研究表明，问题解决能力是在儿童时期发展起来的，对个体的终身发展起到奠基作用。〔3〕儿童在解决问题的过程中，也在形成批判性和系统性思考的能力。〔4〕成人应当发现和保护儿童的好奇心，最大限度地利用自然和实际生活，引导儿童学习如何发现、分析和解决问题。〔5〕因此，对早期儿童问题解决能力的关注和培养非常重要。

已有对问题解决能力的研究大多集中在问题解决能力的内涵、问题解决的过程、问题解决能力的影响因素、问题解决能力的评价与培养等方面。近年来，随着教育测评的出发点逐渐从评估能力向以测助学转变，如何发现和改进个体在认知上的不足之处，进而预测其未来的行为表现，日益成为学者关注的热点问题，而对个体问题解决能力的评价与测量引起了人们的广泛关注。哈珀和皮特森总结了1982—2002 年间关于问题解决能力的研究，并在此基础上研发了《问题解决量表》（Problem Solving Inventory，PSI），从解决问题的信心、趋向-规避风格和个人控制三个方面衡量个体的问题解决能力。〔6〕该量表主要在心理调整、身体健康、环境适应以及职业教育四个领域中应用，测查问题解决能力对专业从业者的影响，以提高他们的生活满意度和幸福感。也有学者针对数学、物理、化学等具体科目设计了问题解决能力测评量表。〔7〕国际学生评估项目（Program for International Student Assessment，PISA）在2003 年首次加入了对问题解决能力的测评，将问题解决能力分为理解、识别、表述、解决、反思和交流问题等方面，〔8〕在2015 年时又强调协作问题解决能力（包含相互理解的能力、采取适当行动解决问题的能力以及建立和维护团队协作的能力）。〔9〕该测试在国内外被广泛用于评价15 岁以上青少年的问题解决能力。我国学者杨滨等人在参考国际学生评估项目的测评方式的基础上，提出质性与量化评价相结合的研究方法，综合分析测查数据、调查问卷、访谈实录、学生作品等，构建了问题解决能力评估模型，〔10〕主要用于初中阶段学生问题解决能力的测评。洪媛媛及其团队对国外大多数研究中采用的诱饵—取回任务进行改编，生成检验工具来检测学前儿童的问题解决能力。该任务主要是将一个具有较强吸引力的玩具放置于设定的问题情境中，学前儿童通过观察和探究情境，借助一些工具取回玩具。该任务包括距离项目、困境项目、烟囱项目等三个项目，最后根据学前儿童是否完成任务以及在完成任务的过程中试错的次数进行五级计分。〔11〕总体来看，国内目前少有专门的、标准化的学前儿童早期问题解决能力评估工具，在一定程度上限制了我国学前儿童问题解决能力研究的进展。

《问题解决能力量表》（Problem Solving Skills Scale，PSSS）是由土耳其学者艾多安等人开发的专门对4—11 岁儿童的问题解决能力进行评估的一项研究工具。该量表的10 个维度能够比较全面地反映儿童问题解决的过程，能够较好地通过科学实证的方式了解儿童的问题解决能力。已有研究表明，《问题解决能力量表》具有良好的信度和效度，预研究的内部一致性系数为KR-20=0.79（N=280），规范研究的内部一致性系数为KR-20=0.81（N=1100）。此外，预研究计算的重测信度为r=0.75（N=31）。〔12〕该量表以测查的形式进行，选用适合儿童年龄和发展水平的选择题题型。该量表通过测查问题解决能力的具体维度，能够更好地了解儿童问题解决能力的发展情况，以便及时提供针对性的支持。该量表最后根据总分确定儿童各年龄段的标准值，用于评估儿童的问题解决能力发展状况。莎海等人和特扎等人分别以该量表为工具探讨STEM 教育计划对5 岁儿童和6 岁儿童问题解决能力的影响，发现接受STEM 教育的儿童的问题解决能力优于只接受基础教育的儿童。〔13，14〕莎海在后续的持久性测试中发现，这种差异会长期存在。穆罕默德等人基于该量表探讨以活动为基础的科学教育实践对5—6 岁儿童问题解决技能习得的影响，发现以活动为基础的科学教育实践能有效提高儿童的问题解决能力。〔15〕因此，将《问题解决能力量表》引入国内，能够弥补国内学前儿童标准化测量工具的不足，可以更全面地了解学前儿童问题解决能力的发展水平，并为未来开发本土化评价工具提供借鉴。

本研究将《问题解决能力量表》翻译成中文，对量表在中国使用的可行性、效度和信度进行初步评估。同时，本研究运用该量表考察了河南省开封市中大班儿童问题解决能力发展水平以及性别和年龄差异，以供相关专业人员参考。

一、研究过程

（一）《问题解决能力量表》简介

《问题解决能力量表》主要采用问题情境解决的方式，根据儿童的回答来评估儿童的问题解决能力。〔16〕本研究选择的是量表中适用于学前儿童的评估内容。量表中的题目是根据解决问题的阶段，按照复杂程度递增的顺序进行分类的，共包含10 个维度，每个维度包含5 个项目。量表另外还有2 个项目作为示例。10 个维度分别为识别问题、定义问题、提出问题、预测问题的原因、确定解决问题的信息充分性、识别问题的组成要素、不同寻常地使用物体、预测一组动作的结果、寻找最合适的解决方案、从许多可能的解决方案中选择最不同寻常的方案。每个项目回答正确得1 分，回答不正确得0 分。量表满分为50 分。每个维度最高得分为5 分，最低得分为0 分。

研究者先和量表原作者联系，获得原作者授权。研究者遵循“翻译—逆向翻译—文化调适—预实验”这一程序，对量表英文版进行翻译及修订。研究者先请2 名学前教育专业研究生将英文量表翻译成中文，再请另1 名研究生对翻译稿进行校对和修改，然后请2 名未曾看过量表原文的英语专业学生将中文译稿译成英语，最后请专家对英语译稿进行审核。结果表明，中译稿和英译稿的内容均与量表原文基本相同，由此形成初稿。然后，研究者请数位学前教育领域专家对中文版量表进行审核，对量表内容以及文化适应性进行再修订，从而形成第二稿。

（二）样本

本研究首先以河南省开封市幼儿园大班儿童为被试进行试测。试测对象为采用随机整群取样方法抽取的河南省开封市幼儿园大班30 名儿童（男孩、女孩各15 名）。正式测试对象为采用随机整群取样方法选取的开封市2 所幼儿园的396 名中大班儿童。剔除无效样本8 名（4 名儿童无法收集得到准确的出生日期，4 名儿童存在数据缺失），实际有效样本为388 名（男孩210 名，女孩178 名），其中中班儿童196 名，大班儿童192 名。

（三）研究程序

本研究在正式施测之前，先按规范要求选取合适样本进行了试测。然后，研究者根据试测结果以及在试测过程中与儿童互动的情况，对量表进行修改，使量表文字表达更加通顺、清晰，更容易为儿童所理解，从而形成量表定稿，即《问题解决能力量表（中文版）》。

取得被试儿童家长同意后，本研究采用经修订后的量表定稿对被试进行正式测试。测试采用一对一方式进行，主试是2 名经过严格培训的学前教育专业研究生。为检验量表的重测信度，间隔1 个月后，研究者随机选取总样本中的30 人进行重测。

（四）数据处理

采用统计分析软件（SPSS26.0 和Amos24.0）对数据进行分析。

二、研究结果

（一）信度检验

1.重测信度

量表的重测信度采用皮尔逊（Pearson）相关系数检验，系数越高，说明重测信度越好。研究者对30 名有效被试进行了前后2 次测量，测量时间间隔为1 个月。前后两次测量得分的相关系数为0.673（p＜0.01），表明差异极其显著。统计检验结果表明，量表的重测信度较好。

改革开放尤其是十八大以来,党中央提出了关于生态文明建设的一系列新理念新要求。在生态文明理念方面,明确提出了“尊重自然、顺应自然、保护自然”“绿水青山就是金山银山”“山水林田湖草是一个生命共同体”等理念。在生态文明与经济社会发展的关系方面,提出了“守住生态与发展两条底线”“良好生态环境是最公平的公共产品,是最普惠的民生福祉”等理念。在生态文明实现路径方面,强调要树立“划定红线,守住底线与资源上限”“像保护眼睛一样保护生态环境,像对待生命一样对待生态环境”等理念。

2.折半信度

根据统计学理论，折半信度法是将测量题目分为对等的两半，根据每个人在这两半测量中的得分，计算两半得分的相关系数，进而估计整个量表的信度。统计检验结果表明，量表的折半信度为0.635，说明两个分量表之间有密切的相关关系，量表跨指标的一致性较好，折半信度良好。

3.内部一致性

一般而言，量表的内部一致性系数在0.80 以上，说明该量表有较好的信度；内部一致性系数在0.70—0.80，是可以接受的范围。〔17〕统计检验结果表明，量表的内部一致性系数为0.70，说明量表具有良好的内部一致性。

（二）项目分析

统计检验结果显示，10 个维度与总分的相关系数均高于0.40，所有相关系数都达到0.01 的显著水平。具体见表1。将问卷总得分最高的27%作为高分组，最低的27%作为低分组，进行独立样本t 检验，〔18〕结果发现每个维度均为高分组得分显著高于低分组（p＜0.001）。

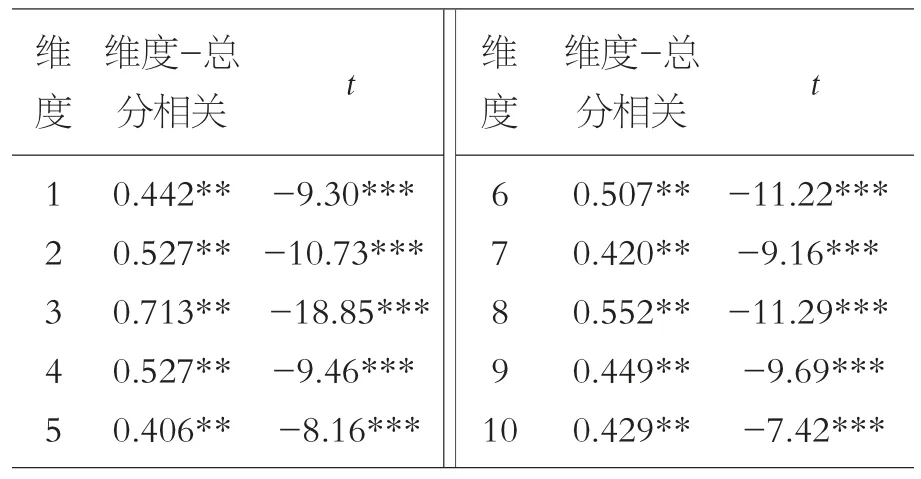
表1 10 个维度的区分度分析（N=388）

（三）效度检验

1.建构效度

检验建构效度最常使用的方法为因素分析，因素分析又可分为探索性因素分析（EFA）和验证性因素分析（CFA）。在本研究中，因为是引进国外的量表，量表结构较为清晰，条目隶属关系较为明确，所以研究者选择对模型直接做验证性因素分析，检验模型的拟合度。〔19〕研究者把10 个维度作为一个潜变量来分析，模型拟合度见图1 和表2。

图1 模型拟合度

表2 验证性因子分析

从模型指数看，模型的卡方自由度比值小于3，近似误差均方根为0.022，多项指标在0.9 以上，说明模型的拟合度比较优秀。

2.效标关联效度

检验测量工具有效性的方法之一是检查其与其他类似的测量工具之间的相关性。从已有相关文献看，批判性思维能力和问题解决能力被认为是两种相关的能力。因此，研究者采用卡沃瑟和阿拜德开发的《儿童批判性思维能力测试量表》（Critical Thinking Skills Test for 5-6-year-old Children，CTTC，2020）〔20〕来检验《问题解决能力量表（中文版）》的标准效度，分析两份量表总分之间的相关性。研究者用《儿童批判性思维能力测试量表》对388 名中大班儿童进行测量，用斯皮尔曼（Spearman）相关系数计算两份量表总分之间的相关性，发现相关系数为0.517（p＜0.001），说明效标关联效度较高。

（四）儿童问题解决能力的发展水平及性别和年龄差异

1.问题解决能力发展水平

对河南省开封市388 名中大班儿童的测查得分进行分析发现，中大班儿童在提出问题、寻找最合适的解决方案以及从许多可能的解决方案中选择最不同寻常的方案等方面的能力还有待进一步发展（见表3）。

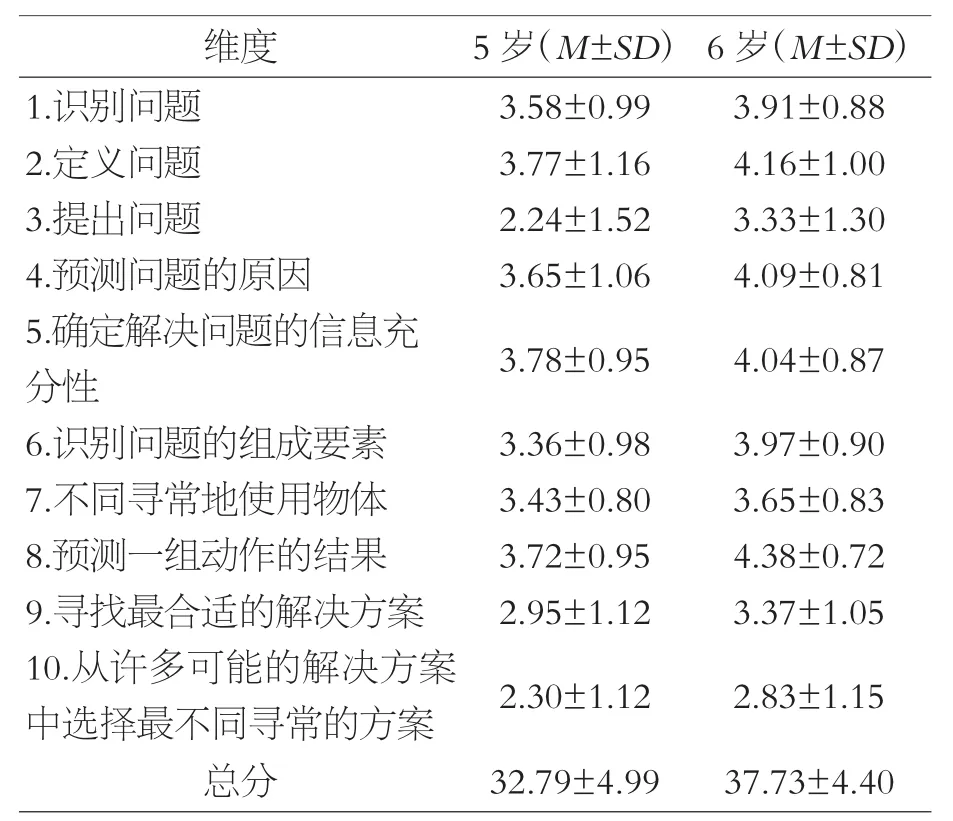
表3 中大班儿童问题解决能力各维度得分

2.性别差异

分析不同性别儿童的问题解决能力得分发现，在问题解决能力总分上，男生（34.99±5.23）和女生（35.52±5.41）之间无显著差异（t=-0.98，p＞0.05）。

3.年龄差异

分析不同年龄组儿童的问题解决能力得分发现，在问题解决能力总分上，不同年龄组之间存在显著差异（t=-10.35，p＜0.05），儿童年龄越大，得分越高，大班儿童得分（37.73±4.40）显著高于中班儿童得分（32.79±4.99）。

三、分析与讨论

（一）关于《问题解决能力量表（中文版）》的心理测量学指标分析

本研究对《问题解决能力量表（中文版）》的测量学指标进行了考察，发现量表具有良好的内部一致性系数（0.70）和折半信度（0.635），表明量表的跨指标一致性较好。重测信度为0.673，已达到可接受范围。从统计学角度看，重测信度的评价还需要考虑特定条件。〔21〕在本研究中，第一次接受测查时被试刚刚进入中班下学期或大班下学期，这时他们对问题解决的敏感性可能还不强。1 个月后，儿童积累了更多的生活经验，问题解决能力迅速提高。问题解决能力的快速发展可能会使某些被试的分数产生较大波动，从而影响到重测信度。就建构效度而言，模型拟合比较优秀。换言之，本研究通过对开封市388 名中大班儿童的测查发现，《问题解决能力量表（中文版）》具有良好的信度和效度。研究者在施测过程中发现，所有被试都能坚持完成测试内容，没有产生厌烦情绪，表明《问题解决能力量表（中文版）》适合中大班儿童的接受水平，适宜对中大班儿童施测。

（二）中大班儿童问题解决能力发展的性别及年龄差异

已有研究显示，早期儿童在学业成就、数学能力等方面有所差异，性别和年龄是常见的影响因素。〔22，23〕本研究之所以分析中大班儿童问题解决能力的性别及年龄差异，是为了考察《问题解决能力量表（中文版）》是否对儿童的性别和年龄差异敏感。结果发现，中大班儿童的问题解决能力在性别方面没有显著差异，在年龄方面差异显著。当然，这可能与抽样有关，还需要做进一步的研究验证。本研究表明，儿童年龄越大，问题解决能力越强。这可能是因为，与年龄小的儿童相比，年龄大的儿童掌握了更多的问题解决技巧，在注意力、语言理解能力、批判性思维、元认知等方面更有优势，从而使其在问题解决能力测试中表现更好。本研究可以得出的结论是，《问题解决能力量表（中文版）》能够有效考察不同年龄儿童的问题解决能力差异。

（三）促进中大班儿童问题解决能力发展的教育建议

借助《问题解决能力量表（中文版）》这一标准化测查工具，教师可以及时了解儿童的发展水平，为得分较低的儿童及时提供问题解决能力的干预与支持。教师应当鼓励儿童发现并描述问题，给儿童提供更多提出问题的机会，让儿童更加善于观察和发现遇到的各类问题。教师应当为儿童提供真实的问题情境，引导儿童分析问题的难易程度，思考问题解决的先后顺序，循序渐进解决问题。在每次问题解决之后，教师应当有意识地引导儿童对自己或者他人的行为进行及时回顾、评价和反思。教师可以鼓励儿童之间相互交流，分享各自面对的问题以及采用的解决方法，还可以在面对较难的问题时组织儿童集体讨论，共同寻找解决问题的对策。幼儿园应当积极推进家园合作，使家长意识到培养儿童问题解决能力的重要性，从而多为儿童提供问题解决的机会和相关支持。