基于可变滑动窗口KLPP的故障检测

郭 金 玉, 郭 佳 燕, 李 元

( 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142 )

0 引 言

主成分分析(principal component analysis,PCA)[1-3]作为一种线性降维算法,广泛应用于工业过程监测。PCA算法可将高维噪声和相关数据压缩到低维子空间。然而大多数工业过程具有非线性特征,PCA可能会忽略非线性系统中的重要信息。为了解决这一问题,核主成分分析(kernel principal component analysis,KPCA)[4-6]被提出。KPCA利用核函数的映射原理,将数据矩阵转换到更高维的特征空间,实现对非线性工业过程的监测。PCA和KPCA算法有效提取数据集的全局特征信息,忽略了局部结构信息,降低了故障检测性能。为了更好地获取样本的局部信息,Hu等[7]提出局部保持投影(locality preserving projections,LPP)算法,通过分析原始数据的局部流形结构,保留有用的局部信息。但是,LPP是一种线性算法,会导致复杂非线性工业过程的监控性能下降。为了进一步提高LPP在非线性过程中的故障检测能力,Deng等[8]提出稀疏核局部保持投影算法,采用特征样本选择技术使核局部保持投影(kernel locality preserving projections,KLPP)模型稀疏化,降低核模型的计算复杂度,并将其在连续搅拌釜式反应器系统上进行实现。张学磊等[9]提出改进核局部保持投影故障检测方法,将KPCA融入KLPP中,使数据包含全局信息和局部信息,提高故障检测率。将多元指数加权移动平均(multivariate exponentially weighted moving average,MEWMA)运用到该方法中提高对微小故障的检测率。

目前,滑动窗口技术也被国内外学者广泛应用于故障检测与诊断领域。滑动窗口的基本原理是通过滑动窗口,抛弃旧的样本纳入新的样本,实现窗口数据的更新。Li等[10]提出递归主成分分析(recursive PCA,RPCA),将新数据加入矩阵更新协方差矩阵,并计算递归的PCA模型,在此基础上递归确定所用的控制限。Wang等[11]提出快速滑动窗口主成分分析(fast moving window PCA,FMWPCA)的应用方案。该方法依赖于RPCA和滑动窗口技术,通过递归计算过程变量的均值、方差和协方差矩阵,实时调整PCA模型,使具有更大的窗口大小的在线应用成为可能,其动态的监控效果要优于静态PCA。Liu等[12]提出滑动窗口KPCA方法,通过实时更新滑动窗口数据进而更新KPCA模型,提高故障检测效果。固定的窗口过大或者过小都会降低检测的正确性,所以调节窗口的大小来适应工业过程的变化的研究方向成为广大学者研究的热点。He等[13]提出一种可变滑动窗口的PCA(variable moving window PCA,VMWPCA)检测方法,该方法在以逐样本和逐块方式递归更新相关矩阵的基础上,将移动窗口技术与经典秩-r奇异值分解算法相结合,构建新的PCA模型。与传统的滑动窗口PCA相比,VMWPCA算法提高了计算效率,降低了存储需求。

为了提高KLPP对非线性工业过程的故障检测能力,增强对时变过程的实时监测能力,本研究提出一种基于可变滑动窗口KLPP(variable moving window kernel locality preserving projections,VMWKLPP)的故障检测方法。利用KLPP可以保持数据结构的局部信息,并结合可变滑动窗口技术,采用样本块更新的方式,滑动窗口并抛弃旧的样本块和纳入新的样本块,以提高运行效率。通过正常过程的变化来调节窗口的大小,改变窗口内的数据样本,进而实时更新KLPP模型以及控制限,提高对非线性和时变特性过程监控的自适应能力。

1 核局部保持投影算法

KLPP算法能够保持原始数据的局部结构。假设原始数据集合X=[x1,x2,…,xN],xi∈m,其中m和N分别为变量个数和样本个数。Φ(·)是KLPP算法的非线性映射,将数据矩阵投影到高维特征空间得到Φ(X)=[Φ(x1),Φ(x2),…,Φ(xN)],这样便于理解和计算。在高维空间中使用LPP算法寻找一个投影矩阵A=[a1,a2,…,al],将Φ(X)投影到低维空间得到保持邻域结构信息的低维数据矩阵Y=[y1,y2,…,yN],即Y=ATΦ(X)。

(1)

ATФ(X)DΦT(X)A=I

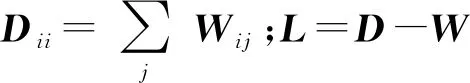
加权矩阵Wij的计算如式(2)所示。

(2)

其中,N(xi,xj)表示xi是xj的k近邻,或者xj是xi的k近邻。t为热核参数,根据经验设定。Wij表示xi和xj之间的近邻关系。

Kij=K(xi,xj)=〈Φ(xi)·Φ(xj)〉=ΦT(xi)·Φ(xj)

(3)

在应用KLPP之前,对核矩阵K进行中心化,得到式(4)。

(4)

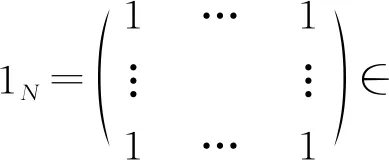
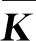
通过求解式(5)的最小特征值所对应的特征向量,得到保留局部结构信息的低维投影矩阵A。

(5)

2 基于可变滑动窗口KLPP的故障检测

2.1 滑动窗口KLPP算法

在滑动窗口KLPP(moving window kernel locality preserving projections,MWKLPP)算法中,移动固定长度的窗口对数据进行测试,当新的正常样本块可用时,通过从KLPP模型中删除最老的样本并添加新样本,从而得到新的窗口数据,用来更新KLPP模型。

(6)

应用T2统计量及其控制限进行故障监测,T2统计量代表特征空间中变量的变化情况。

(7)

其中,Λ是对角矩阵,即Λ=diag(λ1,λ2,…,λl)。

T2统计量的控制限由F分布得到[15]。

(8)

式中:l为样本块中的主成分个数,α为置信水平。

2.2 可变滑动窗口原理

在传统的MWKLPP中,窗口大小是固定的。通常,窗口大小应该足够大,以覆盖建模和监视所需的样本数据。然而,较大的窗口会降低计算效率。当过程快速变化时,该窗口覆盖了太多过时的样本数据,使得MWKLPP无法准确跟踪过程变化。较小的窗口容纳的数据少,可以提高计算效率,但窗口内的数据可能不能恰当地表示出变量之间的关系。太小的窗口可能会导致潜在的危险,因为生成的模型可能会快速地适应变化,以至于无法检测到异常行为。

VMWKLPP方法在k时刻的窗口大小由式(9)计算[16]。

(9)

为了构建稳定的KLPP模型,窗口大小的阈值由式(10)确定。

(10)

Lmax和Lmin由阈值LTh确定。Lmax通常足够大,从而使滑动窗口能够检测某些缓慢变化的故障。Lmax越大,滑动窗口包含的样本数据越多,可能会导致计算效率的降低和模型适应性的退化。考虑到计算效率,Lmax通常取(30～80)×LTh。Lmin越小,说明KLPP模型对过程变化快的适应性越好。为了避免核矩阵的不准确性或不可靠性,Lmin由Lmin～(4～6)×LTh定义,其最小值应该等于阈值LTh。

2.3 基于VMWKLPP的故障检测步骤

考虑窗口大小的变化,采用VMWKLPP方法更新KLPP模型。通过离线建模确定最优的KLPP模型,然后进入在线监测阶段。

离线建模过程:

步骤1收集正常条件下的训练数据集并进行标准化处理,构造初始核矩阵并中心化;

步骤3建立KLPP模型,并确定保留的主成分个数l;

步骤5根据l和m计算阈值LTh,确定Lmax和Lmin;

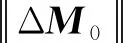
在线监测过程:

步骤2计算新的数据块的核矩阵Knew∈nk+1×L,并且[Knk+1]j=[Knk+1(xnk+1,xj)],其中xj∈m,j=1,…,L是正常样本;

步骤6如果Lk+1≤Lk,确定滑动窗口大小,丢弃旧的(Lk-Lk+1)个样本数据,加入新的样本块后更新程序;否则,将新的样本块纳入确定的窗口后更新程序,并设置Lk+1=Lk+nk+1;

步骤7更新KLPP模型并确定保留的主成分个数;

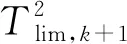
步骤9返回步骤1,直到测试样本全部检测完毕。

3 仿真结果与分析

3.1 田纳西-伊斯曼过程

田纳西-伊斯曼(Tennessee Eastman,TE)过程是一个国际通用的模拟实际工业过程的仿真平台,国内外学者将其广泛应用于故障检测与诊断领域[17-20]。TE化工过程具有变量多、耦合性强的特点。TE过程共包含21种不同类型的故障数据,训练集在正常工况下运行25 h得到500个数据样本,同样测试集运行48 h得到960个样本,其中在测试集中第160个样本后引入故障。

3.2 仿真过程

选取TE过程中的故障2、4、5、7、10、13、14和20作为测试数据,故障具体描述如表1所示。将KLPP、MWKLPP与VMWKLPP方法进行对比,通过误报率和故障检测率两个检测指标来衡量算法的优越性。

表1 TE过程故障描述

KLPP、MWKLPP和VMWKLPP 3种方法采用T2统计量进行过程监控,其中主成分个数均通过85%的累计方差贡献率确定。在MWKLPP中,固定的滑动窗口大小设定为270;在VMWKLPP中,采用基于训练数据集的离线学习得到初始KLPP模型的主成分个数为l=21,从而得到窗口的阈值LTh=16。参数Lmax、Lmin分别设为480(30×LTh)和64(4×LTh),α、β、ξ分别设为0.2、0.2和0.4,另外用测试集进行在线自适应过程监测,块样本包含的样本个数为4。图1给出了故障5的窗口大小Lk的变化情况。可看出,如果数据样本正常,则根据正常过程的变化快慢,可确定新的滑动窗口大小,从而改变窗口内的数据样本,更有效地更新KLPP模型。最后窗口的大小会保持在一个相对稳定的水平,是为了防止模型容纳故障,造成故障检测的不准确性。

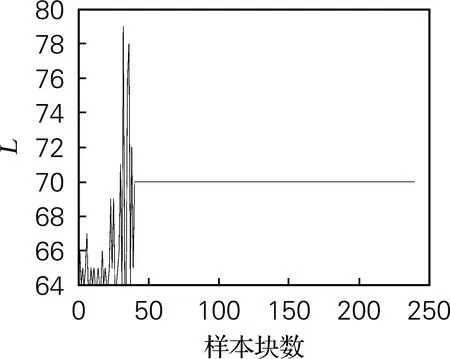
图1 故障5窗口变化

图2为KLPP、MWKLPP和VMWKLPP 3种方法对故障5的监测结果。从图2(a)可以看出,KLPP检测故障5时,故障初始出现可以检测到,但是后续故障都在控制限下方,没有被检测出来。所以,KLPP只能检测出少部分故障数据,具有较低的检测率。从图2(b)中可以看到,使用固定窗口大小的传统MWKLPP方法会产生一定的误报警,且在后续的故障检测中只能检测到少部分故障。与传统的KLPP和MWKLPP算法相比,VMWKLPP方法在没有出现样本误报的情况下检测出了所有的故障。因此KLPP和MWKLPP对故障5的检测结果不理想,而VMWKLPP方法不仅全面地保持数据集的局部结构信息,还可以准确地检测到所有故障。

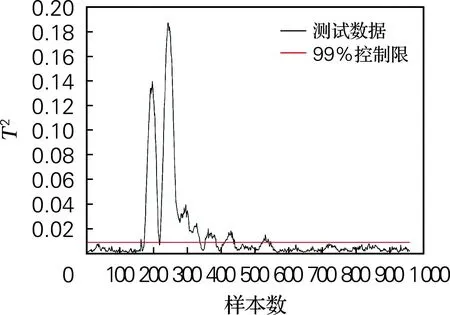
(a) KLPP

表2是3种方法对8种故障的误报率和故障检测率效果。相比KLPP和MWKLPP两种算法,VMWKLPP算法的误报率较低,故障检测率也优于其他两种算法,其中对故障5和故障7的检测率达到了100%。这说明VMWKLPP方法的检测准确性较高,验证了该方法在非线性和时变性的工业过程检测中的有效性和可靠性。

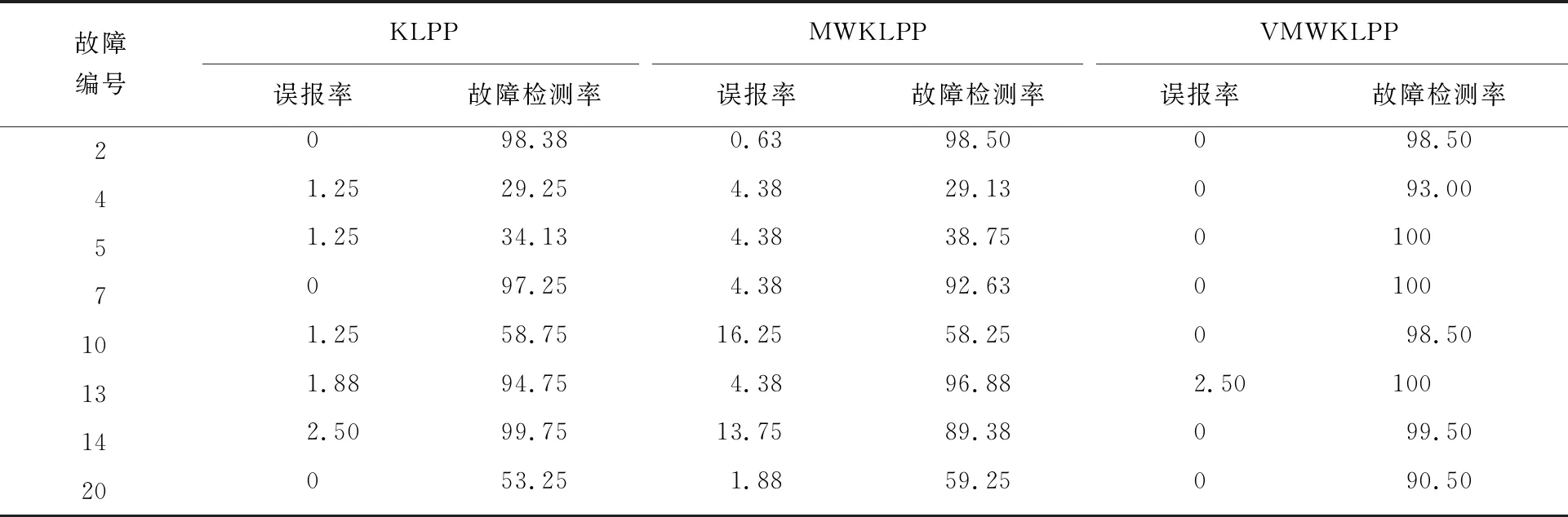
表2 故障检测效果对比

4 结束语

针对现代工业过程存在的非线性和时变性等特点,提出一种基于可变滑动窗口KLPP的故障检测方法。VMWKLPP算法可保留非线性过程数据的局部信息,通过正常过程的变化,可以实时地调节滑动窗口大小,提高运算效率,降低内存需求;动态改变滑动窗口中的数据样本,同时更新KLPP模型以及控制限,实现其对非线性和时变过程的自适应监控。将本文方法应用于田纳西-伊斯曼工业过程,仿真结果表明,与KLPP和MWKLPP方法相比,VMWKLPP方法可以有效地降低误报率并提高故障检测性能,在非线性和时变性的工业过程检测中有明显的优势。所提出的方法对微小故障的效果不是很理想,下一步通过改进检测算法实现对微小故障的故障检测。