基于改进蚁群算法机器人路径规划★
邢协泓, 黄坤荣, 唐德文
(1.南华大学机械工程学院, 湖南 衡阳 412000;2.南华大学核设施应急安全技术与装备重点实验室, 湖南 衡阳 412000)
0 引言
随着社会的发展,机器人在生活、工业生产等方面的应用越来越广泛。机器人进行自由运动的必要条件是其具备路径设计功能,而路径规划的好坏关键在路径搜索算法的选取上[1]。目前对于机器人路径规划提出了多种算法,如:A*算法、D*算法、人工势场法、人工鱼群算法[2]等,与其他算法相比,蚁群算法具有信息正反馈、自组织、并行等特点,所以在路径规划中应用更为方便广泛,但在一些复杂的环境中,传统的蚁群算法也存在一定的不足,如弯折多,收敛速度慢等。随着环境复杂性的提高,对算法的要求也会更高,单一算法往往不能寻找出最优路径。文献[3]将传统蚂蚁群体计算和D*算法结合,通过优化原始D*算法的启发式函数和子节点的方法,用传统蚁群计算的评价方法来改善计算,从而增强了高效性和适应性;文献[4]融合蚁群算法和遗传算法,运用遗传算法的快速搜索对蚂蚁群体计算初始信息素加以处理,避免进入局部优化,并且缩短了寻找路径时间;文献[5]提出了结合Dijkstra 方法和蚁群方法来解决MRPP 问题,实现在最短时间内获得全局最优路径的目标。
蚁群算法是最先提出的模拟蚁群觅食活动的智能模拟算法,该算法由于具有鲁棒性、正反馈等特点,易与其他算法相结合并运用到机器人路径规划中[6]。本文中提出将单一蚁群算法与Dijkstra 算法相互融合,利用Dijkstra 算法的快速全局查询能力,对单蚁群算法的信息素进行处理,并利用Dijkstra 算法实现节点选择,再用蚁群算法进行优化。通过用数学软件MATLAB 模拟,对融合方法和传统算法进行比较,实现优化后的方法通过更短的迭代时间达到了最佳路径设计。
1 传统路径规划算法
1.1 蚁群算法
蚁群计算,是寻求优化途径的一个模拟进化算法[7],是依据蚂蚁觅食的基本原理而得到。蚂蚁在行走的步骤中产生信息素,用以记录自己的步行路程。
在构建路径的每一步中,使用轮盘赌法来选定下一次到达的节点。其节点的选取方程是:
式中:i、j 分别为起点和终点;α 为信息素因子;β 为启发函数因子;τij(t)为时间t 时由i 到j 的信息素浓度;ηij(t)=1/dij(t)是两点i、j 路径距离的倒数;Aallowed,k为尚未访问过的节点的集合。
其中dij表示i、j 之间的欧式几何距离[8],如式(2)所示:
搜索时,由于蚂蚁种类的增多,路径中的信息素含量会相应提高,因为信息元素带有波动性,信息元素含量会随着持续时间的延长而减少。
其表达式为:
式中:τij(t+1)为经过一次更新后路径上的信息素浓度;ρ 为信息素挥发系数且0<ρ<1;为第k 只蚂蚁在路径(i,j)上的信息素增量;N 为蚁群总数量;Q为信息素增量系数;Lk为第k 只蚂蚁搜索经过的路径长度。
1.2 Dijkstra 算法
Dijkstra 算法是一种经典的求解最短路径的算法,用于计算一个节点到其他各个不相关节点的最小移动价值[9]。
在路径规划中,先假定起点为s,再引入S 和U。S记录已求出最短路径的顶点和相应的最短路径长度的集合,U 记录还未求出最短路径的顶点以及该顶点到s 的距离的集合。如果所找出的点到一节点的路不通,则距离视为∞。
Dijkstra 算法在节点的选取过程中实质上从某个节点出发,然后沿着地图的边通过路径到达另一节点,再选取在每条边上权重之和最小的路径[10-12],将相邻的下一个节点进行标记,比较起点到下一节点的距离大小,筛选出离起点较短的节点,删除较长的节点。在改进的算法中,只需要将障碍物的各顶点加入到U 中,这样既缩短了搜索时间,又使得搜索更具有导向性,路径更短。
2 改进蚁群算法路径规划
本文改进蚁群算法的基本思想是搜索初期使用Dijkstra 算法重新进行节点的选取,使其将搜索目标向最优解靠拢,再用蚁群算法优化节点寻找最优路径,防止机器人离障碍物太近。
2.1 路径规划环境建模
环境建模的方法有栅格法、拓扑法、可视图法等[13]。由于栅格法直观且建模容易,本文采用栅格法进行环境建模。图1 是栅格法的基本模型,20 cm×20 cm 格子表示机器人所处总环境,黑色格子表示环境中的障碍物,没有障碍物的自由移动环境用白色格子表示每一格为1 cm。在建模过程中,可能存在不足一格的现象,应进行膨化处理,不足一格用一格代替[14]。

图1 栅格法环境建模
在栅格图中坐标表示为:
式中:b 为栅格边长;mod 为取余;ceil 为取最小整数;xi,yi为每个栅格的坐标位置[15]。
2.2 节点选取
机器人在寻找最短路径时,首先要越过障碍物,文献[16]中介绍了越过圆形障碍物的可达路径,即从起点经过圆的切线,如图2 所示。
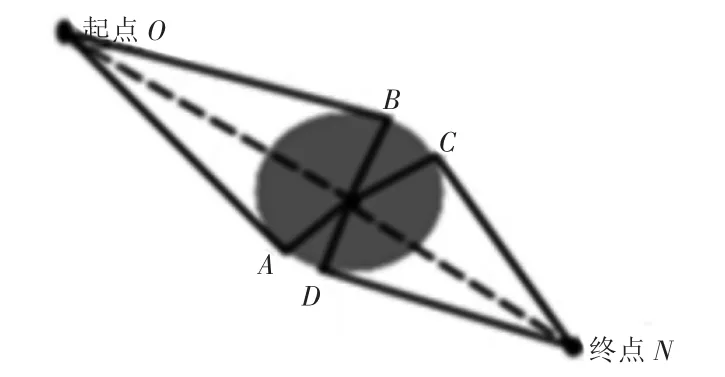
图2 经过圆形障碍物可达路径[16]
基于此,本文改进算法引入切点,在栅格法建模的环境中,将障碍物的顶点看成切点,如图3 所示,正方形ABCD 为障碍物,起点为O,终点N;从起点到终点,按照圆形障碍物可达路径方式,越过栅格环境有4 条路径,分别为O→B→N;O→C→N;O→A→N;O→D→N。但考虑无法直接越过障碍物,机器人会选择B、C 作为中间节点。
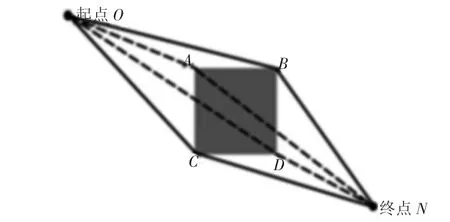
图3 经过栅格环境障碍物可达路径
将改进后的可达路径与传统算法进行比较,如图4 所示。

图4 改进与传统路径比较
图4 所示,OMN 为传统路径,OCN 为改进路径,OE+EC>OC,CF+FN>CN,EC=MF,CF=EM⇒OM+MN>OC+CN,改进后的路径比传统路径更短且更优。
由图4 对比可知,机器人会选择走经过B、C 两点的路径。若选择经过A、D 两点,则需要绕过障碍物,路径的权重之和变大,则Dijkstra 算法的S、U 表中将删除A、D 两点。
2.3 节点优化
经过多个障碍物时,先将所有障碍物的端点进行标记加入到U 表中,用Dijkstra 算法选择出权值和最小的路径,而当离障碍物很近时,直接用Dijkstra 算法进行节点选择时会让路径可行性降低,改用蚁群算法进行路径更优化选择。
优化原则:在栅格法建模的环境中,当蚂蚁离障碍物的水平距离少于一个单位时,用蚁群算法选择水平点,如图5 所示。
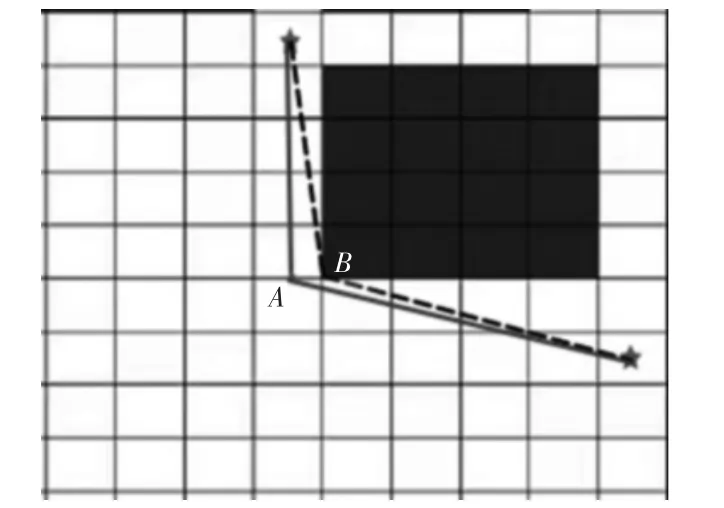
图5 蚁群算法优化原理
设起点坐标O(x0,y0),B 点坐标(x1,y1),则A 点坐标为(x0,y1),将式(3)进行更新,得到:
更新后的启发式函数计算如式(8)所示:
如图5 所示,障碍物在起点右方,用优化后的算法更新后得到A 点。B 点为Dijkstra 算法找出的权值最小的点,A 为蚁群算法优化找出的节点。在三角形OAB 中,OB 为斜边,OA 为直角边,直角边比斜边短,权重更小,A 为最优点,将B 点从U 表中删除,A点放入U 中。
用蚁群算法优化更新后的距离更短,路径更优,同时也避免了机器人在移动的过程中与障碍物发生碰撞,实现了路径最优的要求。
2.4 改进蚁群算法
在未知环境中,将蚁群算法和Dijkstra 算法相融合,使机器人在路径规划中,初期使用Dijkstra 算法将搜索目标向最优解靠拢,再用蚁群算法寻找最优路径。机器人遇到障碍物时,利用融合算法将切点作为节点放入S 进行搜索,选择距离起始点最近的切点,若切点离障碍物过近,再将切点平移后的点移到U中,随后更新信息素以及迭代次数,输出最优路径,其算法流程如图6 所示。
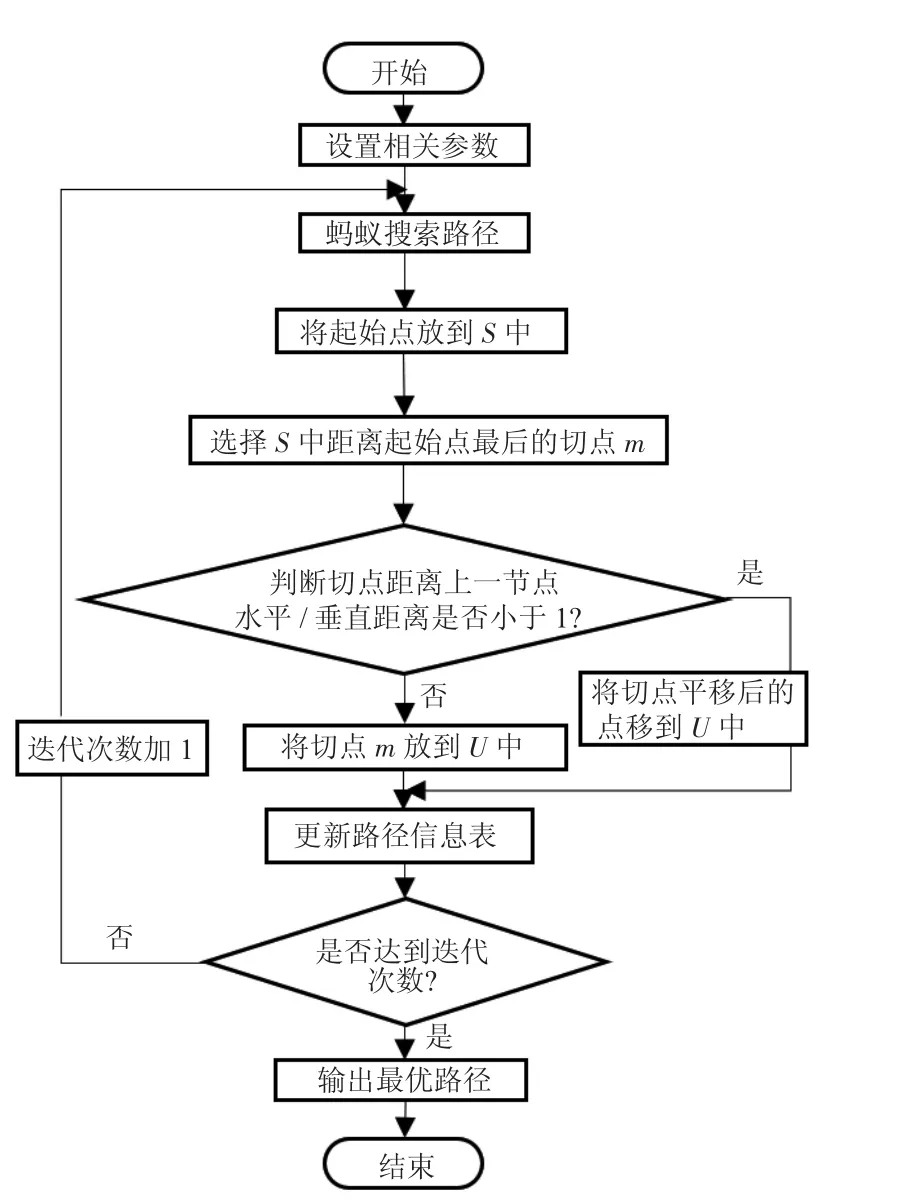
图6 融合算法流程
3 仿真结果与讨论
本文采用MATLAB_R2022a 进行仿真,对机器人在建立的已知地图上进行实验,分别运行传统蚁群算法以及本文改进融合蚁群算法,从最短路径长度、迭代次数、运行总时间这三方面分析比较,实验环境建模如图1 所示,设置的蚁群初始参数如表1 所示,起点为(0.5,19.5),终点为(19.5,0.5)。

表1 蚁群算法初始参数
仿真结果中,图7-1 为传统蚁群算法路径规划,图7-2 为改进融合蚁群算法路径规划,对比可知,传统算法路径轨迹有14 个弯折点,改进后的算法有7个弯折点,融合后的蚁群算法比传统蚁群算法路径弯折点减少了50%,路径更为平稳。
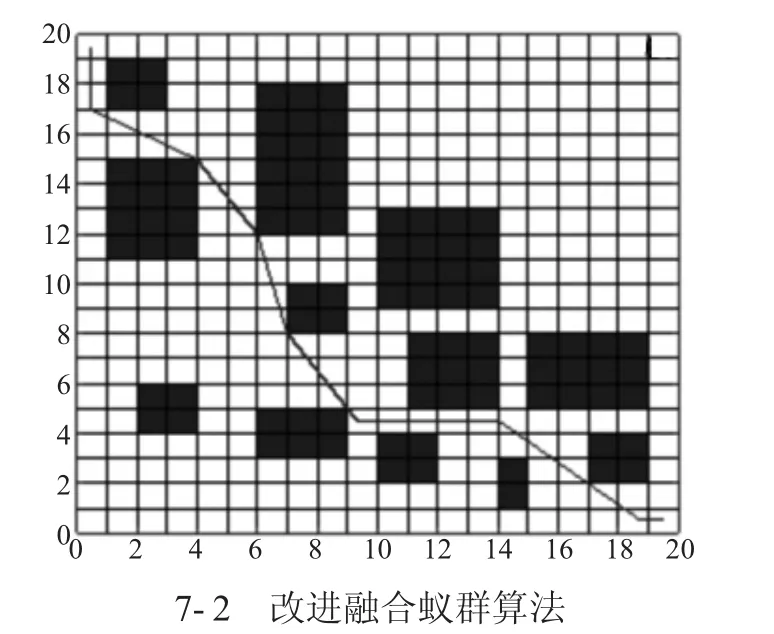
图7 传统与改进算法路径规划对比
图8-1 为传统蚁群算法收敛曲线,迭代次数在50 次趋于平稳,最短路径为30.38 cm;图8-2 为改进融合蚁群算法收敛曲线,可知最小路径迭代到32 次时趋于平稳,最短路径为26.21 cm。迭代最短路径由30.38 cm 降到26.21 cm,迭代次数由50 次降到32次,可见改进后的算法路径更优,搜索效率更高。
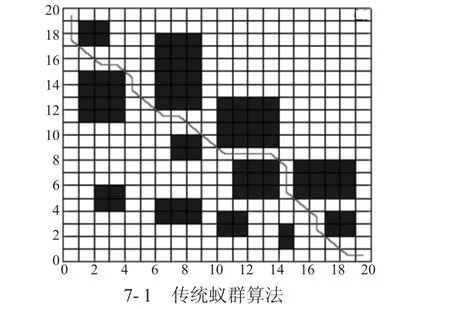
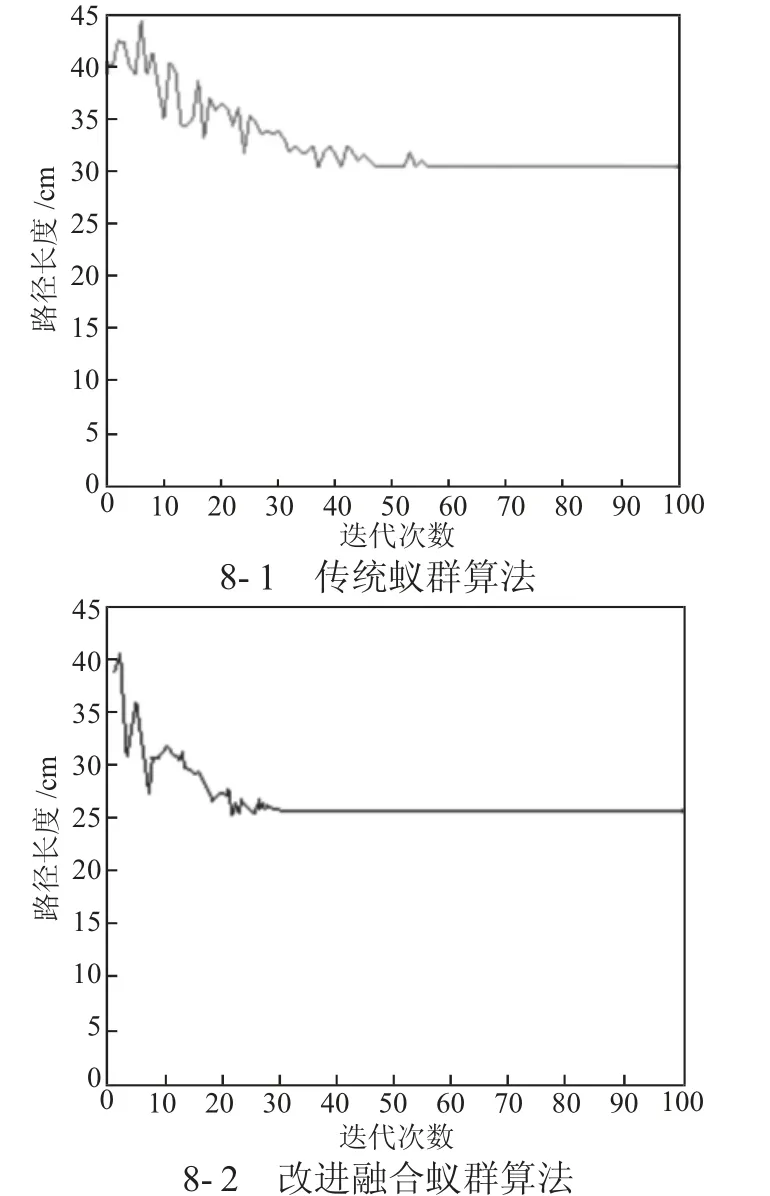
图8 传统与改进算法收敛曲线对比
综上,数据对比如表2 所示,传统蚁群算法的最短路径为30.38 cm,迭代次数为50 次,而经过优化融合后的蚁群算法的最短路径为26.21 cm,迭代次数为32 次,减少了40%的路径长度,同时改进后的算法也增加了收敛效率,相比于传统蚁群算法增加了37%,优化后的算法执行时间大大缩短,搜索效率更高,路线弯折更少。

表2 数据对比
4 结语
本文采用了栅格法环境模型,面对蚁群算法中收敛速度慢且极易陷入局部求解的难题,提出了融合Dijkstra 算法与蚁群算法的方法:搜索初期用Dijkstra算法引入切点向最优解靠拢,后期用蚁群算法优化节点选择。实验表明,在同一环境下改进后的算法路径长度缩短了14%,收敛速度提高了37%,弯折点减少了50%,在路径长度、迭代次数、搜索时间、弯折点等方面均优于传统蚁群算法。利用MATLAB 仿真证实了融合后的算法可以进一步提高收敛速率,并使得搜索的路径更有引导性,相比于常规的蚁群方法,经过改进后的方法路径弯折更少,易获得最优的路径。

