外推的MHSS迭代法求解一类大型稀疏的复对称线性系统
李贝贝, 崔静静, 黄政阁, 谢晓凤
(广西民族大学数学与物理学院, 广西 南宁 530006)
1 引言
考虑求解如下大型稀疏线性方程组
其中A∈Cn×n是一个复对称的非Hermitian 正定矩阵, 其形式为
其中W,T∈Rn×n分别是对称正定和对称半正定矩阵. 这里是虚数单位, 假设T≠0, 则A是非Hermitian 正定矩阵.
在科学与工程计算的领域中, 如固体力学、科学计算、动力学、工程计算、非线性规划等[1-4]都需要求解复对称线性系统(1). 目前, 求解复对称线性系统(1) 常用的方法有直接法和迭代法两大类. 当系数矩阵阶数较小时通常可采用直接法求解, 但当用直接法求解大型稀疏矩阵方程组时会破坏系数矩阵的稀疏性, 从而增加计算机的存储量,降低计算效率. 而迭代法具有可充分利用和保持系数矩阵的稀疏性, 节省计算机存储空间等优点, 因此在求解大型稀疏线性系统时, 更倾向于使用迭代法. 近年来, 数值迭代方法在许多数学领域中都有极为广泛的应用, 例如: 四元数方向[5], 微分方程方向[6-7]等. 鉴于复对称线性系统来源的广泛性, 本文针对此类问题构造一种有效的迭代算法,促进相关领域的发展. 在求解复对称线性系统的已有迭代法中, 其中最著名的迭代法是基于Hermitian 和反Hermitian 方法的迭代法. 首先对系数矩阵A进行Hermitian 和反Hermitian 分裂:
这里H和S分别是矩阵A的Hermitian 和反Hermitian 部分. 根据A的Hermitian 和反Hermitian 分裂,白中治、Colub 和Ng 提出了求解复对称线性系统(1)的Hermitian和反Hermitian 分裂(HSS) 迭代法[8]; 基于HSS 迭代方法, 白中治、Benzi 和陈芳提出了改良的HSS(MHSS) 迭代方法[9]; 潘春平、王红玉和曹文芳提出了外推的HSS(EHSS)迭代方法[10]. 此外, 基于HSS 迭代法, 许多改进及推广的相应迭代法被提出. 例如, LHSS 迭代方法[11], PHSS 迭代方法[12], PMHSS 迭代方法[13], LPMHSS迭代方法[14], AHSS 迭代方法[15], APMHSS 迭代方法[16]和QHSS 迭代方法[17]等.
潘春平等对HSS 方法使用外推技术得到EHSS 方法. EHSS 方法在迭代次数和计算时间方面都优于HSS 迭代方法, 具体可参考文献[10]. 下面简单介绍一下EHSS 迭代方法.
EHSS 迭代方法:设A∈Cn×n是正定矩阵, 给定一个初始向量x(0)∈Cn, 计算
直到迭代序列{x(k)} 收敛, 这里α是给定的正常数,ω是非负常数,I是单位矩阵.
EHSS 迭代法可等价地表示为
其中这里M(α,ω) 是EHSS 迭代方法的迭代矩阵. 实际上, 迭代格式(2) 可由系数矩阵A进行如下分裂得到
其中
HSS 迭代方法在求解线性系统时每一步迭代都需要求解一个位移反Hermitian 线性系统, 这无疑是困难和耗费时间的. 为解决这个问题, 白中治、Benzi 和陈芳提出了改良的HSS(MHSS) 迭代方法, 文献[14] 中的数值实验结果表明MHSS 迭代法无论是在迭代次数还是计算时间上都优于HSS 迭代方法. 下面简单介绍一下MHSS 迭代方法.
MHSS 迭代方法:给定一个初始向量x(0)∈Cn, 计算
直到迭代序列{x(k)} 收敛, 这里α是给定的正常数,I是单位矩阵.
迭代格式(3) 可以改写为
其中
M(α) 是MHSS 迭代方法的迭代矩阵. MHSS 迭代方法也可以看做是由矩阵A进行如下分裂所得到的
其中
然而, EHSS 迭代方法在求解线性系统时每一步迭代也都需要求解一个位移反Hermitian 线性系统, 且MHSS 迭代法在求解某些复对称线性系统时收敛速度比较慢, 为了克服这些缺点, 受EHSS 迭代法思想的启发, 考虑对MHSS 迭代方法使用外推技术, 期望能得到比EHSS 和MHSS 方法更好的结果.
本文的具体布局为: 在第二节中构造了外推的MHSS(EMHSS) 迭代方法; 第三节研究了EMHSS 迭代方法的迭代矩阵与MHSS 迭代方法的迭代矩阵之间的关系, 并讨论了EMHSS 迭代方法的收敛条件; 第四节给出的数值实验说明了本文方法的有效性。
2 EMHSS 迭代方法
受EHSS 迭代法思想的启发, 考虑对MHSS 迭代方法使用外推技术, 构造了外推的MHSS 迭代法, 简称为EMHSS 迭代法.
根据EHSS 方法, 考虑迭代格式(3) 中的第一步迭代
在上述等式两边同时乘以i, 并移项可得
将上式带入格式(3) 中的迭代格式
可得
再结合
可得如下迭代格式
联立MHSS 迭代法中的第一步迭代, 有
在(5) 式中引入松弛参数ω, 可得
结合迭代格式(3) 中的第一步迭代和(7) 式可得到如下的外推MHSS(EMHSS) 迭代法.
外推的MHSS(EMHSS) 迭代法:任给一个初始向量x(0)∈Cn, 计算
直到迭代序列{x(k)} 收敛, 这里α是给定的正常数,ω是非负常数,I是单位矩阵.当ω=1 时, 该方法即为迭代格式(6).
经过简单的计算, 外推的MHSS(EMHSS) 迭代方法可表示为
其中
和
这里L(α,ω) 是EMHSS 迭代法的迭代矩阵.
如果引入矩阵
和
则有下列等式成立
则EMHSS 迭代法(8) 可看作是对A进行上述分裂(10) 所得到.
3 EMHSS 迭代方法的收敛性分析
定理3.1设A=W+iT∈Cn×n, 其中W∈Rn×n,T∈Rn×n分别是对称正定矩阵和对称半正定矩阵. 令α,ω分别是正实数和非负实数,M(α) 和L(α,ω) 分别是MHSS迭代方法和EMHSS迭代方法的迭代矩阵, 则有
其中η=(1+i)ω-2i.
证明由(4) 式可得
则
因此, 根据上式和(9) 式可得
定理3.2设A=W+iT∈Cn×n, 这里W∈Rn×n,T∈Rn×n分别是对称正定矩阵和对称半正定矩阵. 假设A是正规矩阵, 则W和T满足WT=TW. 设λj和µj(j=1,2,··· ,n) 分别是矩阵W和T的特征值. 设λmax和λmin分别为矩阵W的最大特征值和最小特征值,µmax为矩阵T的最大特征值. 如果0 ≤ω<2, 则有
(1) 若0<α≤1,µmax-λmin≤, 则ρ(L(α,ω))<1;
证明如果W∈Rn×n,T∈Rn×n满足WT=TW, 则存在正交矩阵Q, 使得
其中
由(9) 式可知
ρ(L(α,ω))<1 成立需满足不等式而
若2αλj(α+λj)(α+µj)>2α2(µ2j+λ2j) 成立, 即
则必有不等式(11) 成立.
(1) 当0 <α≤1 时, 如果µmax-λmin≤, 必然满足µj-λj≤λ2j, 则有不等式2αλj(α+λj-αλj)+2µj(αλj+λ2j-αµj)>0, 即ρ(L(α,ω))<1.
(2) 当α> 1, 如果, 必然满足, 则2αλj(α+λj-αλj)+2µj(αλj+λ2j-αµj)>0, 即ρ(L(α,ω))<1.
4 数值例子
本节通过数值实验验证EMHSS 迭代方法求解复对称线性系统的有效性, 并在迭代次数(IT), 计算时间(CPU) 和相对残差(RES) 方面将其结果与EHSS 和MHSS 方法进行了比较. 所有数值实验均在Intel(R)Core(TM)i7-8700 CPU @3.20GHz 和RMA 16.0GB,Win7 系统的电脑上用MATLAB R2018b 进行的.
在本次实验中,所有测试迭代法选取均以零向量x(0)=0作为初始迭代向量. 所有测试迭代法的终止准则是当k步的相对残差满足
时, 计算停止.
例4.1[9]Ax=(W+iT)x=b满足线性系统(1), 其中
e1和em分别是第一个元素和第m个元素为1 的单位向量. 选取右端向b=(1+i)A1,这里1是所有元素都为1 的向量.
表1 列出了在不同问题规模下MHSS 迭代方法和EMHSS 迭代方法求解例4.1 时的实验最优参数. 表2 给出了在表1 的参数下MHSS 迭代方法和EMHSS 迭代方法求解例4.1 时的迭代次数(IT), 计算时间(CPU) 和相对误差(RES). 另外, 由于EHSS 迭代方法求解例4.1 时是不收敛的, 因此在表1 和表2 中未列出EHSS 迭代方法的实验结果. 观察表2 可知, 当矩阵规模相同时, EMHSS 迭代方法的迭代次数(IT) 和计算时间(CPU) 都少于MHSS 迭代方法的计算时间和迭代次数. 除了m= 64 外, EMHSS迭代方法的相对误差(RES) 都要优于MHSS 迭代方法. 因此, 从数值实验的结果可知EMHSS 迭代法的计算效率要优于MHSS 迭代法.

表1 EMHSS 和MHSS 迭代方法求解例4.1 时的最优参数取值
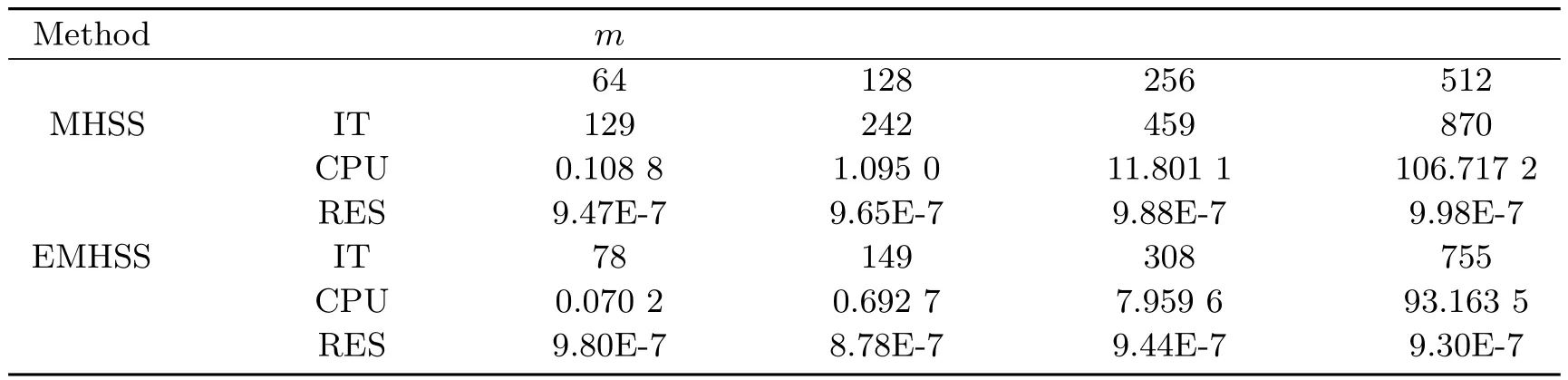
表2 EMHSS 和MHSS 迭代方法求解例4.1 时的最优参数取值
例4.2[11,18]考虑复Helmholtz 方程
其中σ1,σ2是实系数函数,u在[0,1]×[0,1] 上满足Dirichlet 边界条件. 使用步长为的五点差分格式去处理上述方程, 可得如下类似线性系统(1.1) 的方程
这里
H是一个阶数为n的块三对角矩阵, 且n=m2, 选取右端向量b= (i-1)A1, 这里1是所有元素都为1 的向量. 通常在上述等式的两边同时乘h2来正规化系数矩阵. 在实际计算中取σ1=σ2=10, 则矩阵H+σ1I和矩阵σ2I是对称正定的.
表3 列出了在不同问题规模下MHSS, EHSS 和EMHSS 迭代方法求解例4.2 时当迭代次数达到最少时参数α和ω的取值范围. 在表4 中, 给出了MHSS 和EHSS迭代方法的迭代次数和计算时间均最少的实验最优参数取值, 及在最优参数下的迭代次数(IT), 计算时间(CPU) 和相对误差(RES). EMHSS 迭代方法中参数α,ω选取为α=10, 及在α=10 的情况下ω的最优取值, 及在此情况下的迭代次数(IT), 计算时间(CPU) 和相对误差(RES). 从表4 中可以看到当问题规模相同时, 虽然EMHSS迭代方法的相对误差与MHSS 和EHSS 的相对误差几乎相同, 但EMHSS 迭代方法的迭代次数(IT) 和计算时间(CPU) 要少于MHSS 和EHSS 迭代方法迭代次数(IT) 和计算时间(CPU). 因此可知当α= 10 时, EMHSS 迭代方法已经优于MHSS 和EHSS迭代方法. 若α和ω都选取为最优参数时, EMHSS 迭代方法必然有更好的数值实验结果. 总之, EMHSS 迭代方法求解复对称线性系统时的计算效率比MHSS 和EHSS 迭代方法的计算效率高.
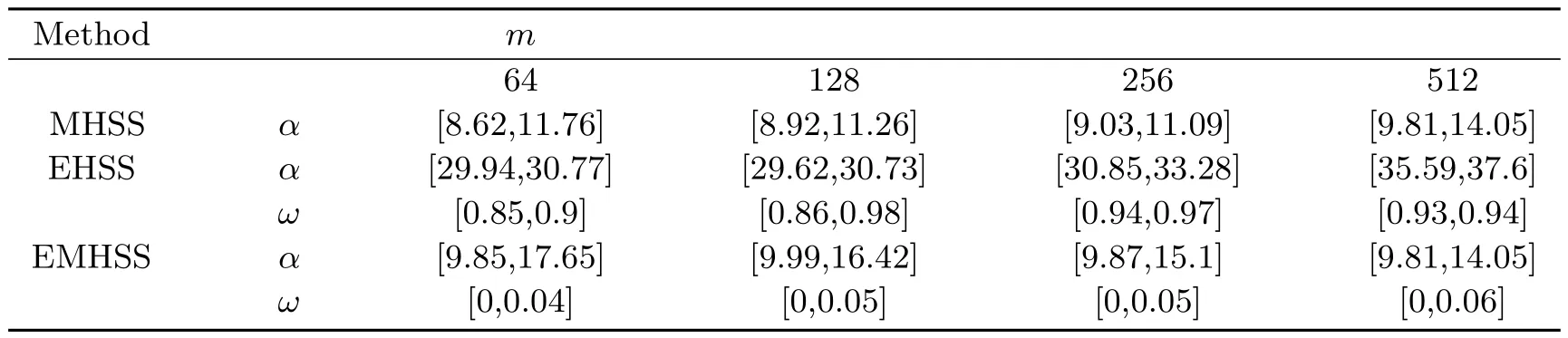
表3 EMHSS, EHSS 和MHSS 迭代方法求解例4.2 时的最优参数取值范围
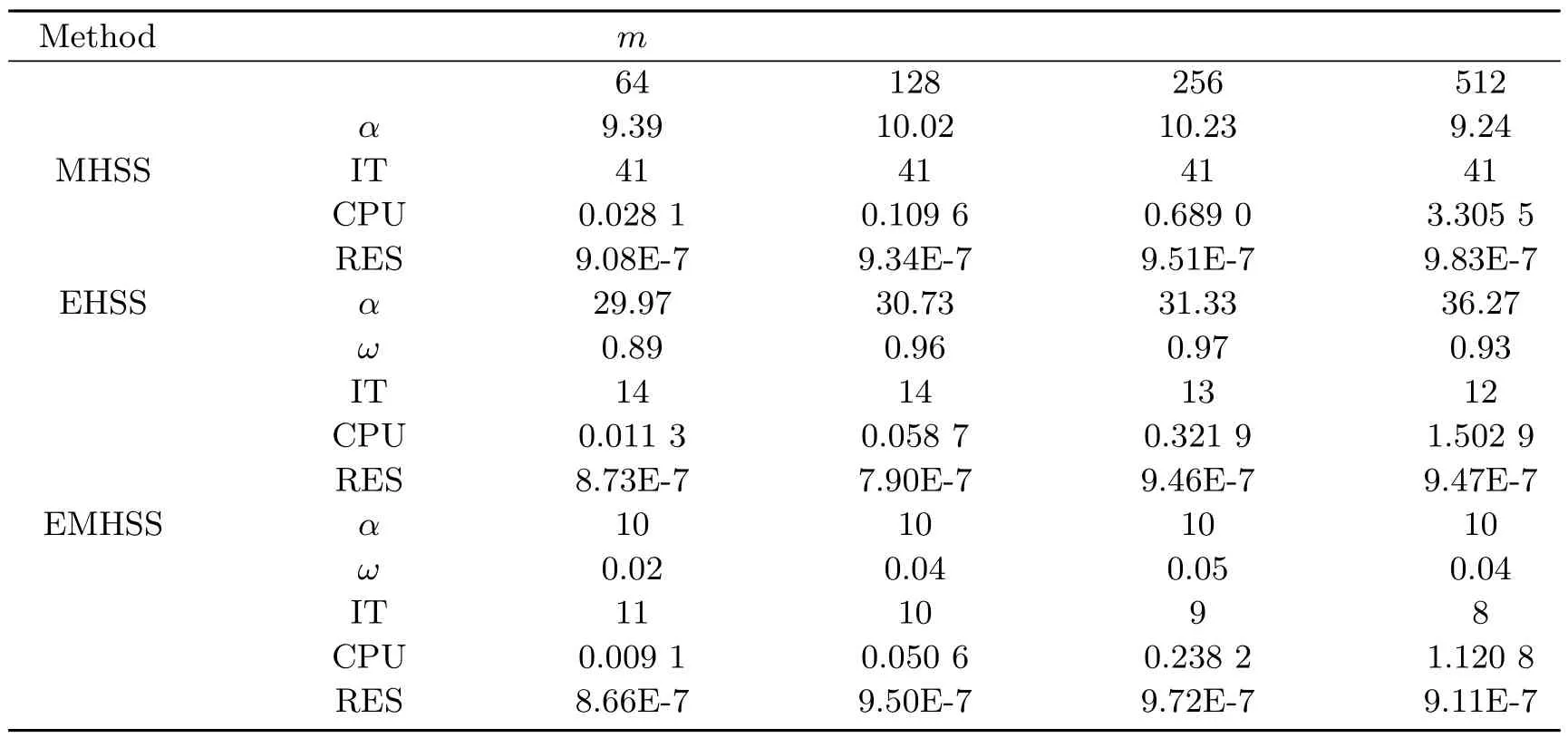
表4 求解例4.2 时EMHSS, EHSS 和MHSS 方法的迭代次数, 计算时间和相对残差
例4.3[9]考虑形为如下的方程
这里M和K是惯性矩阵和刚度矩阵,CV和CH是粘性矩阵和滞后衰减矩阵,ϵ是驱动循环频率. 令CH=εK, 这里ε是一个衰减系数,M=I,CV= 10I,K是在均匀网格[0,1]×[0,1] 且网格大小为上使用中心差分格式沿着负Laplacian 算符方向均匀的逼近Dirichlet 边界条件形成的矩阵. 这里
另外, 选取右端向量b=(1+i)A1, 这里1是所有元素都为1 的向量. 通常在上述等式的两边同时乘h2来正规化系数矩阵. 在实际计算中分别取ϵ=1 和ε=0.002.
表5 给出了MHSS 和EMHSS 迭代方法求解例4.3 时迭代次数达到最少的参数的取值范围. 表6 在表5 给出的参数范围的基础上, 展示了迭代时间最少时的参数值, 迭代次数, 迭代时间和相对残差. 从表6 可知随着问题规模的增大MHSS 和EMHSS 迭代方法的迭代次数逐渐增大, 且EMHSS 迭代方法的迭代次数远小于MHSS 迭代方法的迭代次数. 同时, EMHSS 迭代方法的迭代时间也少于MHSS 迭代方法的迭代时间.另外, EHSS 迭代方法求解例4.3 时的时间花费非常大, 最优参数的选择是困难的, 因此在表5 和表6 中未列出EHSS 迭代方法的数值实验结果.

表5 EMHSS 和MHSS 迭代方法求解例4.3 时的最优参数取值范围
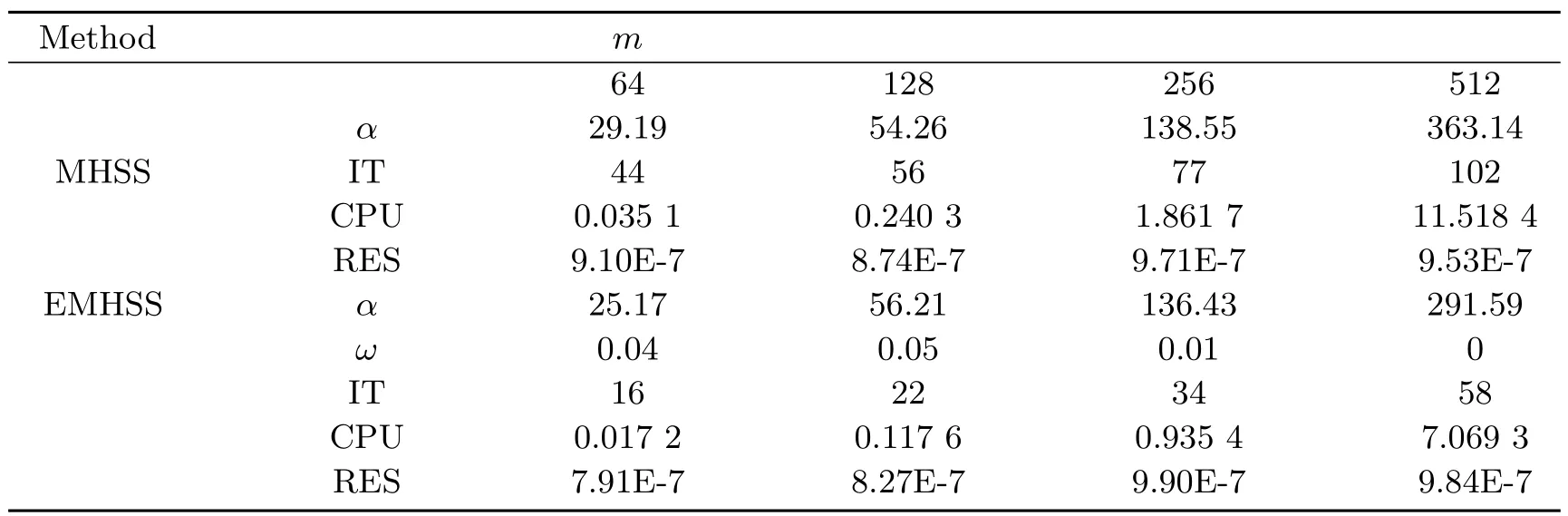
表6 求解例4.3 时EMHSS 和MHSS 方法的迭代次数, 计算时间和相对残差
此外, 为了更直观地观察EMHSS, MHSS 迭代方法对参数α的敏感性, 在图1 中给出了当m=64 时三个例子的迭代次数(IT) 随参数α的变化曲线. 另外, 因为EHSS迭代方法求解例4.2 时是收敛的, 因此中间图还展示了EHSS 的迭代次数随参数α的变化曲线. 从图1 可以看到当参数ω不变时, MHSS 和EMHSS 迭代方法求解三个例子时迭代次数随着参数α的增大均是先减小后增大. 且也可看出不管参数α如何选取,EMHSS 迭代法的迭代次数均小于MHSS 迭代法的迭代次数, 且迭代次数最小值是远小于MHSS 迭代方法的最小值.
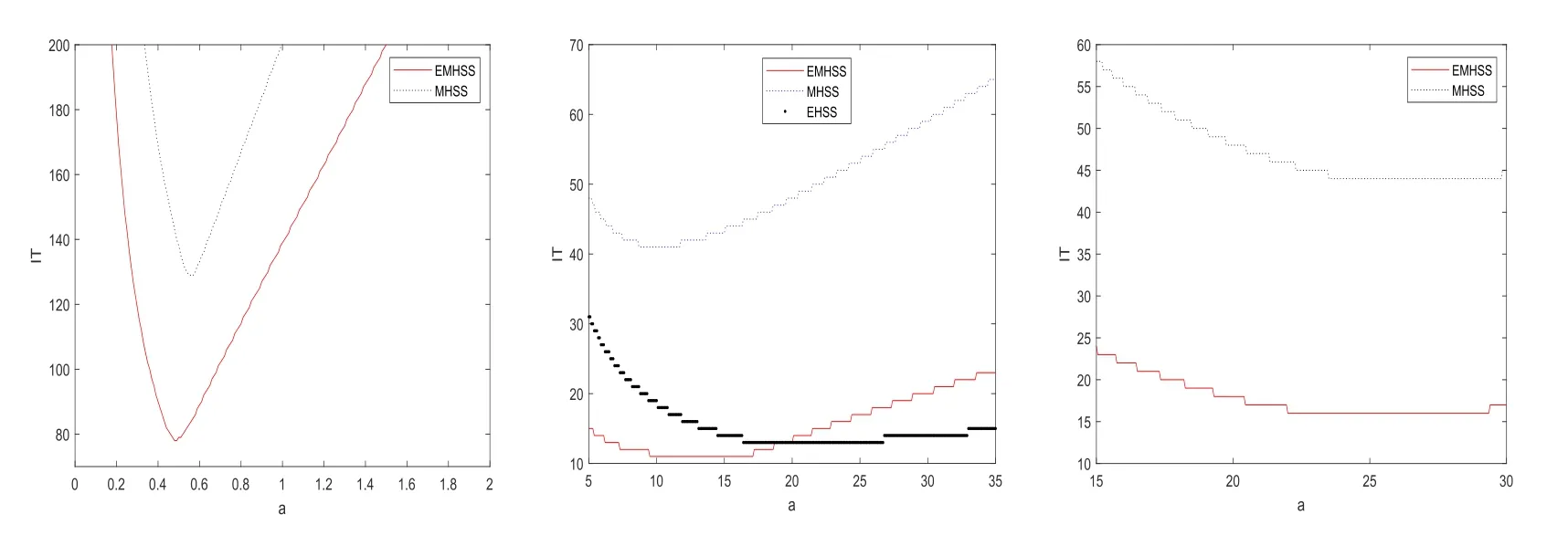
图1 m=64 时EMHSS, MHSS 和EHSS 方法的迭代次数随参数α 的变化图
图2 直观地展示了EMHSS 迭代方法当m=64 且参数α固定时(例4.1:α=0.49;例4.2:α= 10; 例4.3:α= 25) 单一变量ω对迭代次数的影响. 从图2 可以观察到三个例子的迭代次数均是在ω接近于0 时达到最少.
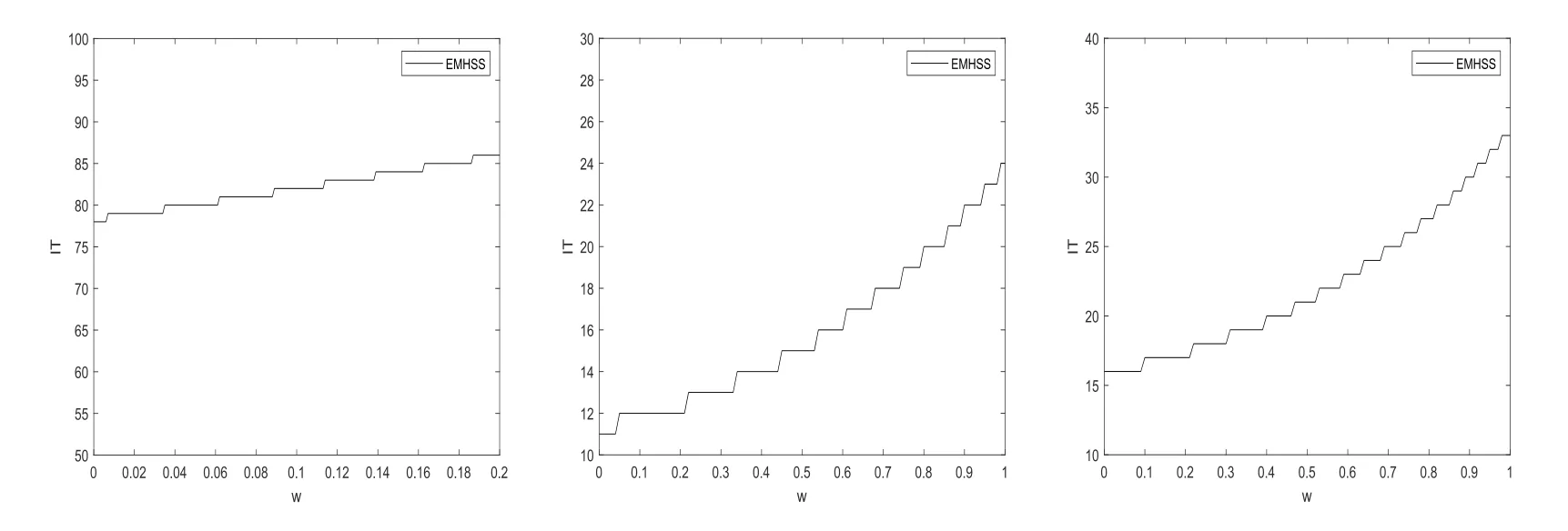
图2 m=64 时EMHSS 方法的迭代次数随参数ω 的变化图
同时, 图3 画出了当m=64 时, EMHSS 迭代方法求解这三个例子时, 迭代次数随参数α和ω变化的三维图像. 从图3 的左侧图可看到EMHSS 迭代方法求解例4.1 时,当α在0.5 附近时迭代次数达到最少. 从图3 的中间图可以看出EMHSS 迭代方法求解例4.2 时, 当α在0.2 附近,ω在10 附近时迭代次数达到最少. 且从图1 - 图3 可知,EMHSS 迭代法求解复对称线性系统时具有较高的计算效率.
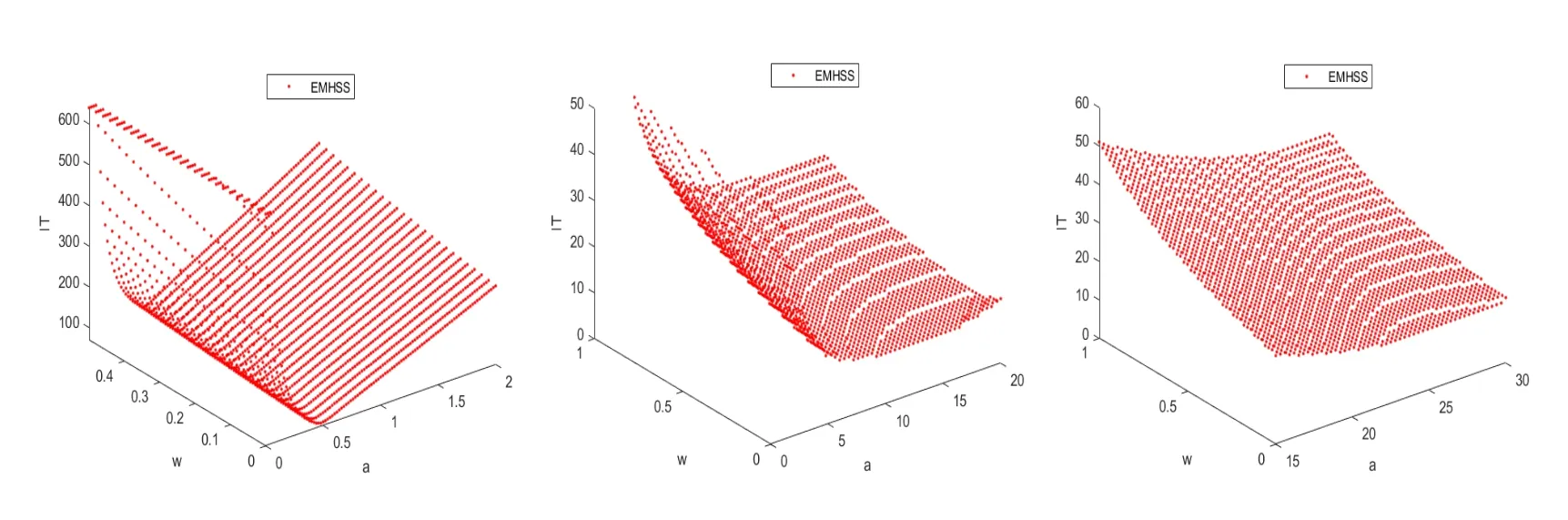
图3 EMHSS 迭代方法的迭代次数随参数α 和ω 变化的三维图像
5 总结
本文基于EHSS 迭代法的思想对MHSS 迭代法采用外推技术提出了外推的MHSS(EMHSS) 迭代方法. 并给出了EMHSS 迭代法的迭代矩阵和MHSS 迭代法的迭代矩阵之间的关系, 且讨论了EMHSS 迭代法收敛的条件. 最后通过数值例子, 从迭代次数,计算时间和相对误差方面说明了EMHSS 迭代法的有效性. 另外, 还给出了EMHSS 迭代方法的迭代次数随着参数α变化曲线图, 以及参数α和ω对EMHSS 方法的迭代次数影响的三维变化图, 说明了求解复对称线性系统时EMHSS 迭代方法优于EHSS和MHSS 迭代法.
- 纯粹数学与应用数学的其它文章
- Multiplicative eccentricity resistance-distance of unicyclic graphs with a given parameter
- Research on multi-factor stock selection model based on random forest algorithm
- 一类离散无向图模型诱导的概念类的样本压缩方案
- 一类高维多响应变量误差模型的极小极大下界
- Almost primes in generalized Piatetski-Shapiro sequences
- On primes in kth-power progressions on average

