斜拉索桥梁雷电暂态分布特性研究
史雅静,柴健,徐达军,邳莹,孙京
(1.湖北省防雷中心,武汉 430074;2.中国气象局雷电重点开放实验室,北京 100081;3.武汉雷光数字科技有限公司,武汉 430074;4.中国气象局武汉暴雨研究所中国气象局流域强降水重点开放实验室/暴雨监测预警湖北省重点实验室,武汉 430205)
引言
随着经济的快速发展,桥梁作为必不可少的交通设施也得到了迅速发展,据不完全统计,仅长江干流先后建成及在建的跨江大桥数量已逾150 座,我国已跃升为世界桥梁强国。然而,这些跨江、跨海桥梁多位于水陆交界处,环境空旷,桥梁的塔顶多处于周围环境的制高点,极易遭受雷击,因此桥梁的雷电防护工作越来越受到关注和重视。
近年来很多学者针对不同类型桥梁的雷电防护工作开展了大量研究。秦玉新等(2010)以南宁大桥为例,重点介绍了长跨度桥梁直击雷和感应雷防护工程的设计技术和施工要点;李良福等(2015)对缆索承重桥的缆索防雷技术开展研究,指出缆索易遭受天面和侧面的雷击,长时间雷击是影响缆索使用寿命的主要因素,并提出了桥梁缆索的防雷措施;孙汝杨(2020)选取某铁路工程斜拉索桥梁为研究对象,结合铁路综合接地系统特点,对桥梁的防雷接地系统设计进行了重点探讨;王毅力(2020)以重庆蔡家嘉陵江大桥为例,介绍了桥梁防雷设计方案,并对设计中关键技术要点进行了探讨;陈景荣等(2023)根据防雷等级和设计原则,对港珠澳大桥青州航道桥主体防雷设计方案进行了探讨。张娟等(2014)对影响斜拉索桥雷击风险的相关因子进行了研究,指出在实际的风险计算中应充分利用闪电定位资料,并结合周围雷电环境合理选择相关因子的修正系数,使风险值尽可能结合实际,并且还定量分析了斜拉索桥遭雷击产生的各类损失风险概率。上述研究中,对桥梁雷电防护技术的研究多以现行技术规范为依据,从工程角度分析设计和施工的技术要点、研究桥梁的雷击风险,以定性分析为主,定量分析较少。
雷击现象发生时,雷电流通过雷击点注入,将在泄流通道中形成强大的暂态电流,进而引起电压的升高,威胁设备安全运行和人身安全(殷启元等,2019;李鑫等,2021),雷电灾害对国民经济和人民生命财产造成的危害和损失越来越大(余田野等,2019;郑劲光和蔡小琴,2019;李霞等,2021)。因此,国内外大量学者针对雷电暂态特性开展研究,但大多针对杆塔、建筑物或金属构筑物等(Cholinezhad J et al,2019;朱泽伟等,2019;彭程等,2022),对桥梁的相关研究还较少,主要有张岩等(2014)对桁架桥梁开展了雷电暂态特性研究,提出了基于耦合传输线网络模型的桁架桥防雷系统的建模方法,分析了桁架桥在遭受直击雷时金属构架上的瞬态电流分布、电磁场分布规律,但研究中为了减少计算量将桥梁导体简化为21 根,模型相对简单。从开展雷电暂态特性研究的方法来看,目前应用较多的软件主要有EMTP(Electro-magnetic Transients Program)(陈宋,2018;张萍等,2020)和CDEGS(Current Distribution Electromagnetic Interference Grounding and Soil Structure Analysis)(曾勇等,2017;黄瑞莹等,2018;史柳等,2018),相对前者,CDEGS软件基于电磁理论,不受频率限制,分析结果更为精确(王尚,2016)。因此,本文利用CDEGS 软件,选取在跨度较大的桥梁中得到广泛应用的斜拉桥为例,根据桥梁设计资料,在尽可能还原桥梁导体真实布设情况的基础上建立三维模型,同时选取30 多个雷电流频率点,研究一般斜拉索结构桥梁的塔顶、斜拉索和桥面分别遭受直击雷时,桥梁磁场、跨步电压及雷电流分布情况,以期为桥梁防雷工程设计提供参考。
1 雷电暂态分布计算原理
1.1 雷电流模拟
雷电流可以用双指数函数来表示(张小青,1996)
雷电流分布的计算宜在频域中进行,故用离散傅里叶变换来表示雷电流,即
式(1)和式(2)中i(t)、I(ω)和I0分别为随时间变化的雷电流幅值、随频率变化的雷电流幅值和雷电流峰值,单位均为kA。t和j表示时间和虚数,A为峰值系数,α和β分别为波前衰减系数和波尾衰减系数。当雷电流波形为10/350 μs 时,取A=1.025,α=2.05×10-3,β=0.564。
1.2 电路等效
当实际电路的最大尺寸远小于雷电流的波长时,符合集总参数电路的应用条件,可以用电路基本定理进行求解。本文选定分段导体的长度为10 m,导体的分段等效电路如图1 中从上至下第二个虚线框内所示,考虑到模型中每根导体都处于空气介质中,故导体的电导可以忽略不计。经过上述处理后,待求模型就转化为一个仅含电阻、电感和部分电容的等值网络,原钢筋结构的雷电暂态计算也转化为这种等值网络的暂态计算。
本文桥梁模型中等效的分段导体数量设置了3 119 根,为了简化整个桥梁的等效电路图,如图1 所示,用省略号代替了多根相似导体的等效电路,从上至下第一个虚线框内为等效的斜拉索导体,第二个虚线框内为等效的桥面导体,第三个虚线框内为等效的桥墩导体即接地装置。其中桥面钢筋主要起到等电位的作用,对模型计算分流及磁场结果的影响较小,因此将其等效为一整块金属板,如图1 中第二个虚线框内的等效电路。
1.3 等效矩阵网络计算
由于桥梁中的导体数量较多,为了方便计算雷电流在频域下的解,采用矩阵网络基尔霍夫方程进行计算。假设主放电通道支路顶端的节点有一频率为ω的电流Is注入,设该模型的等效网络共有n个独立的节点、b条支路,其中主放电通道有l1个子导体段,构架共有l2个子导体段及l3条接地电阻支路,则有b=l1+l2+l3。依据基尔霍夫电流定理和电网络理论,可以列出主放电通道支路的电流电压向量混合列矩阵(戴传友,2001)。
其中A为n×b阶的节点关联矩阵,为b×1阶的支路电流列向量,Y为n×n阶的节点导纳矩阵,为n×1阶的节点电位列向量,为n×1阶的电流源列向量,Z为b×b阶的复阻抗矩阵,G为b×n阶的电压系数矩阵。
采用列主元消去法即可求得单个雷电流频率下各支路电流和节点电压的频域解。为了满足计算精度的要求,通过求解多个雷电流频率下的解,然后利用傅里叶逆变换即可求得导电构架电流分布及各节点电压的时域解。
2 模型建立
2.1 研究对象
本文选取湖北省的一座单塔斜拉索桥梁作为研究对象,建立该桥梁的三维模型(图2),并在塔顶、斜拉索和桥面分别设置了模拟雷击点,同时设置了用于计算磁场强度分布及跨步电压分布的3处观测面。该桥梁主桥全长328 m,含引桥桥面为360 m,宽21 m,索塔距离桥面高96 m,桥面距地面高14 m,索塔采用“琵琶”形,塔身偏离铅锤面10°,倾向岸侧,斜拉索76根,沿桥梁中心线两侧对称布置,自然接地体775根,分布在5 个桥墩中。大桥按照第二类防雷建筑物进行设计,采用共用接地系统,根据国家标准《建筑物防雷装置检测技术规范》(中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会,2015),接地电阻值设计要求小于等于4 Ω。塔顶设长度为4 m的φ76 mm×6 mm不锈钢管为接闪杆,索塔自下而上敷设4根40 mm×4 mm的热镀锌扁钢作为引下线,利用五组桥墩基础作为自然接地装置。配电箱等电子信息设备设置在距离桥面以下4.6 m处,如图2中索塔下横梁的放大示意部分。同时,为了防止侧击雷,将76 根斜拉索与接地干线、引下线的金属构件可靠连接作为自然接闪器。
2.2 参数设置
2.2.1 雷电流参数
仿真试验中将雷电流设置为幅值150 kA,10/350 μs的双指数雷电流波形(图3),其中10 μs 表示雷电流波前时间,350 μs表示半峰值持续时间。
2.2.2 桥梁参数
根据上述桥梁真实设计数据设置桥梁模型参数,并等效设置桥梁导体材料,斜拉索等效设置为Φ 9 mm圆钢,大桥桥墩中的导体材料等效设置为Φ 19 mm圆钢,其中作为自然接地体的桥墩内圆钢在最顶部进行首尾圆弧连接,底部直接与土壤相接触,相当于垂直接地体。
图4为桥面斜拉索位置俯视分布图。桥面的左下角设置为坐标轴原点(0,0,0),右上角坐标为(360,21,0)。76根斜拉索沿桥面中轴线呈对称布置,一侧依次标号为1—38 号,其中1 号斜拉索的坐标为(0,10,0),38 号斜拉索的坐标为(290,10,0);另一侧从左往右依次标号为39—76号,其中39号斜拉索的坐标为(0,11,0),76号斜拉索的坐标为(290,11,0)。

图4 桥面斜拉索位置分布俯视图Fig.4 The aerial view of the location distribution of the stay cables on the bridge deck
2.2.3 土壤参数
一般河水的电阻率为30~600 Ω·m(陈先禄等,2002),与一般土壤电阻率较接近。为了简化土壤模型,将实际桥梁正下方的水域等效为单层结构的土壤,土壤电阻率ρ设置为100 Ω·m。
3 模拟结果及分析
基于以上试验参数设置,利用CDEGS软件进行建模和仿真计算,得出直击雷分别击中桥梁的塔顶、斜拉索和桥面时,桥梁电子信息设备安装处的磁场、桥面下方地面处的跨步电压、桥梁斜拉索及接地体上的雷电流分布规律。
3.1 磁场暂态分布特性分析
雷击放电过程中会产生强大的磁场,尤其是在用于分流的引下线附近,磁场达到最大值。一般桥梁在设计时都会考虑安装用于照明的配电设备及用于通信传输的电子信息设备。模型选取斜拉索桥常见的电子信息设备安装位置,即如图2 所示,在索塔桥面以下4.6 m 处设置与桥面平行的,观测面长80 m,宽15 m,模拟计算观测面B 处的合成磁场分布。如图5a—c,当桥梁的塔顶、斜拉索和桥面遭受雷击时,观测面b 的磁场强度峰值分别为1 440.13 A·m-1,2 023.98 A·m-1和1 169.70 A·m-1。

图5 雷击桥梁的塔顶(a)、斜拉索(b)和桥面(c)时观测面B(图2)合成磁场强度峰值分布(X,Y代表相应观测面的长度和宽度,下同)Fig.5 The amplitude peak distribution of synthetic magnetic field on the observation surface B(figure 2)when lightning strikes(a)the tower top of the bridge,(b)the stay cables,and(c)the bridge deck.X and Y represent the length and width of the observing surface,hereafter
当雷击斜拉索时,由于大量的雷电流通过单根斜拉索,造成了电流分布极不均匀,因此在观测面的中心位置,即索塔琵琶造型处两侧产生的磁场强度峰值最大,为2023.98 A·m-1。雷击桥面时,可将桥面看成一个金属板,大量的雷电流经桥面钢筋横向传导后流经引下线上的垂直电流只有一小部分,因此观测面处产生的磁场强度峰值最小,约为雷击斜拉索时产生的磁场强度峰值的一半。雷击塔顶时,大部分雷电流经4根引下线分流,由于两侧各有两根引下线,因此图5a中出现了磁场强度双峰的现象。
根据上述结果可以得出雷击斜拉索桥梁时磁场强度分布的一般规律:电子信息设备安装位置的磁场强度值与靠近安装位置处引下线上雷电流的大小、安装位置距离引下线的远近均有关。电子信息设备安装位置离引下线距离越近且引下线上雷电流越大,周围产生的磁场强度值越大。当雷击斜拉索时产生的磁场强度峰值最大,雷击塔顶时次之,雷击桥面时最小。一般斜拉索桥梁电子信息设备安装在下横梁处,因此在设计电子信息设备安装位置时除了应尽量远离用于分流的引下线外,还应考虑最严酷情况下(即雷电流出现的最大可能幅值及雷击斜拉索时)电子信息设备处的磁场强度值是否在安全阈值范围内,即800 A·m-1(全国信息技术标准化技术委员会,2011)。
3.2 跨步电压暂态分布特性分析
当桥梁遭受直击雷时,地面处会产生较大的跨步电压,如不做好接地网的均压措施或者地面的绝缘处理,将可能对桥面下活动的人员造成伤害。因此在桥梁两端桥面以下14 m地面处设置跨步电压观测面,靠近索塔端地面处为观测面A、远离索塔端地面处为观测面C(如图2),观测面A、C长均为60 m,宽为41 m,来模拟桥梁塔顶、斜拉索和桥面分别遭受直击雷时,跨步电压峰值的分布情况。如图6a、b,当桥梁塔顶遭受直击雷时,观测面A和C处跨步电压峰值分别为7.62 kV和13.04 kV,斜拉索遭受直击雷时,观测面A和C处跨步电压峰值分别为8.58 kV 和18.13 kV(图6c、d),桥面遭受直击雷时,观测面A 和观测面C 处跨步电压峰值分别为3.02 kV和16 kV(图6e、f)。
从图6可见,桥梁遭受雷击时,观测面A越靠近第二组接地体(如图2)的位置,跨步电压峰值越大,而观测面C 在第三组接地体位置处,其跨步电压峰值较大。观测面A的跨步电压峰值均远小于观测面C跨步电压峰值,这是因为观测面A斜拉索及索塔引下线的分布较集中,电流分布较均匀,且与起主要散流作用的第二组接地体即索塔位置相距较远,而观测面c 在第三组接地体的附近,且在雷击分流的边缘位置,电流分布较不均匀,故跨步电压值较大。从桥梁不同位置遭受直击雷时的跨步电压分布可以看出,雷击斜拉索时跨步电压峰值最大,这是因为雷击单根斜拉索时产生的电流分布极不均匀,因此产生的跨步电压值较大。而雷击桥面时由于雷电流分布较为均匀,产生的跨步电压值较小。
3.3 电流暂态分布特性分析
3.3.1 斜拉索电流分布
根据雷击塔顶时的模拟结果可以得出斜拉索上峰值电流的分布规律。图7为单根斜拉索的雷电流幅值随时间的变化曲线,可见峰值电流的波前时间约为8 μs,由于未经过桥面及塔身内钢筋导体的分流,雷电波的折反射效应不明显,因此与起始雷电流的波前时间较相近。提取所有斜拉索及索塔两侧塔身上波前时间为8 μs处对应的峰值电流进行算术相加,得到总电流和为150.24 kA,与起始雷电流幅值十分接近,验证了软件计算的准确性。

图7 单根斜拉索上雷电流幅值随时间的变化Fig.7 The temporal variation of lightning current amplitude on a single stay cable
图8为斜拉索单侧(如图4中1—38号)峰值电流分布图。由于两侧斜拉索上的电流分布近似一致,这里只绘制了一侧斜拉索上的峰值电流分布。图中峰值电流呈现上下起伏的趋势,在索塔处即雷击点位置雷电流峰值达到最大,约为4.8 kA,斜拉索编号为19号。最小峰值电流仅为0.35 kA。
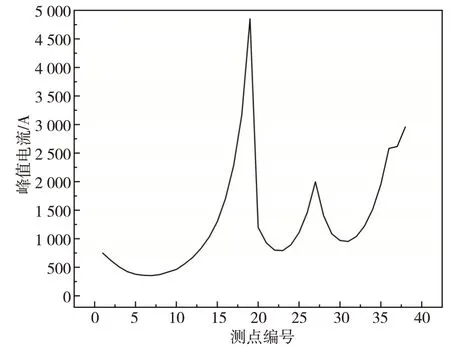
图8 斜拉索单侧峰值电流分布Fig.8 The peak current distribution of one side of the stay cable
19—38 号斜拉索处的雷电流峰值大小呈双峰双谷变化趋势,这是由于19—38号斜拉索下方的三组接地体位置在远端,雷电波的折反射效应明显,且由于距离较远,中间位置斜拉索上的雷电流由于受到相互屏蔽效应的影响,会产生中间位置雷电流减小,两端雷电流增大的变化趋势。19 号斜拉索正下方就是接地体的位置,雷电流通道最短,因此泄放的雷电流峰值最大。1 号斜拉索虽然正下方也有接地体,但斜拉索长度较长,由此产生的雷电流通道较长,因此与19号斜拉索上分得的雷电流峰值相比较小。由于屏蔽效应,1—19号斜拉索上的雷电流分布也是呈中间小、两端增大的变化趋势。因此斜拉索雷电流的大小分布与雷击点位置、斜拉索长度以及接地体位置密切相关。
3.3.2 接地体电流分布
模型中设置了五组接地体(如图2)。图9 为每组接地体中单根钢筋引下线的雷电流幅值随时间的变化。其中第一组和第五组接地体由于处在模型的边缘位置,导体间的互感互容效应不大,导致峰值电流的波前时间变化较小,分别约为4 μs 和9 μs。而第二、三、四组接地体处在接地模型的中间,存在大量的接地导体,因此对雷电流波形的影响较大,峰值电流的波前时间分别约为45 μs、75 μs和32 μs。而每组接地体中的钢筋电流分布基本一致,为了简化计算,设置每组接地体中的所有钢筋上的雷电流峰值出现在同一时间。将每组接地体中的峰值电流进行算术和计算,分别得到第一至五组接地体的总电流分别为43 kA、48.67 kA、30.334 kA、9.458 kA和11.625 kA。

图9 图2中五组接地体中单根钢筋的雷电流幅值随时间的变化Fig.9 The temporal variation of lightning current amplitude of single reinforcement in five groups of grounding systems in Fig.2
由于每组接地体的电流波形不同,因此算术和相加得出的总电流与起始电流幅值有所不同,但通过电流的大小,可以得出电流的大概分布趋势。其中位于索塔位置的第二组接地体的雷电流最大为48.67 kA,承担了大部分雷电流的泄放,第四组接地体的雷电流最小为9.458 kA
接地体上雷电流的大小分布与雷击点位置及接地体的布设位置密切相关。离雷击点位置越近的接地体上的雷电流幅值越大。当几组接地体布设的较近时,处于中间位置的接地体由于受到屏蔽效应的影响,将呈现雷电流大幅减小的现象。处于边缘位置的接地体上的雷电流波前时间变化不大,对原始雷电波陡度的削减作用不明显,而处于中间位置的接地体上雷电流波前时间呈现大幅升高的趋势,相当于将原始雷电波陡度进行了削减,降低了雷电波因陡度大而造成的危害。
4 结论与讨论
利用CDEGS软件,选取湖北省一座单塔斜拉索桥梁为例,分别模拟计算桥梁的塔顶、斜拉索和桥面遭受最严酷的直击雷时,桥梁周围的磁场、跨步电压及雷电流分布情况,得到以下主要结论:
(1)雷击斜拉索时,桥梁电子信息设备安装处磁场强度峰值最大,雷击塔顶时次之,雷击桥面时最小;雷击斜拉索时桥梁下方地面处的跨步电压峰值最大,雷击桥面时桥梁下方地面处的跨步电压峰值最小。
(2)单根斜拉索雷电流的大小分布与雷击点位置、斜拉索长度以及接地体位置密切相关。斜拉索下方离接地体位置越近且斜拉索长度越短,分得的雷电流幅值越大;当斜拉索下方离接地体位置较远时,由于屏蔽效应使得中间位置斜拉索上雷电流减小,两端位置斜拉索上雷电流增大。
(3)接地体上雷电流的大小分布与雷击点位置及接地体的布设位置相关。离雷击点位置越近,接地体上的雷电流幅值越大,布设在中间位置的接地体由于屏蔽效应雷电流呈现雷电流大幅减小的现象;处于布设在边缘位置的接地体上的雷电流波前时间变化不大,对原始雷电波陡度的削减作用不明显,而处于布设在中间位置的接地体上雷电流波头时间呈大幅升高的趋势,降低了雷电波因陡度大而造成的危害。
本文尽可能按照实际大桥中钢筋结构的数量、斜拉索的布设方式、土壤的特性等进行建模,导体数量达3 119根,运算量庞大。因此,在考虑桥梁下方的水域部分时,将其等效为地面土壤区域,作为单层土壤进行有限元的计算。此外本文结论只针对常规斜拉索桥结构,而对于雷电流参数的设置,也仅考虑了最严酷的情况。未来可对多种雷电流波形及不同幅值的雷电流参数进行设置模拟,为实际工程应用带来更多参考。

