基于广义谐振理论的输电线路无源干扰谐振频率求解

漆 照，刘传彬，李丹丹，沈 浩，马国庆

（1.山东中实易通集团有限公司，山东 济南，250003；2.国网山东省电力公司电力科学研究院，山东 济南，250003；3.国网山东省电力公司，山东 济南，250000）

0 引言

在国家新基础设施建设的背景下，输电线路对周边无线电台站的无源干扰现象越来越严重［1-2］。根据现有研究成果，获取干扰谐振频率，从而制定防护距离是解决输电线路无源干扰的关键［3-5］。然而，由于环境和特高压输电线路路径的复杂性，加之无线电台站允许的干扰水平不一致，很难通过实验方法确定谐振频率。

输电线路无源干扰问题主要研究模型为电场积分方程［6-7］，由于电场积分方程涉及大量积分运算，主要采用矩量法［8-10］对其进行离散求解。1996年，IEEE 在Trueman C.W.和Tilston M.A.等人［11-12］的研究基础上，根据天线理论［13］，提出中波频段（0.535～1.705 MHz）输电线路无源干扰水平极值的预测方法，即“整数倍波长回路谐振频率”和“四分之一波长谐振频率”，上述方法忽略了铁塔的细节，仅以细导线代替铁塔整体。当频率超过1.7 MHz 时，根据文献［3，14］研究结论，铁塔的角钢、辅材都将影响输电线路在外界激励下的电磁散射，即铁塔细节变得不可忽略。因此，IEEE 明确指出其方法仅适用于1.7 MHz 以下频率的无源干扰谐振频率预测。文献［15］基于矩量法研究输电线路的无源干扰，证实在1.7 MHz 以上仍然存在明显的干扰谐振现象。然而，由于缺乏相应的理论，针对1.7 MHz 无源干扰谐振问题，截至当前，仍只能依靠矩量法进行扫频计算，从而获得观测点处的无源干扰极值。采用矩量法扫频计算确定干扰极值时，必须改变计算条件多次进行计算，从而造成计算量过大等问题。

针对上述问题，采用系统函数的思想，研究输电线路与无线电台站构成系统整体的电磁散射特性，从而将研究多天线系统的广义谐振理论［16-17］引入大尺寸的输电线路无源干扰研究中。通过少量频点的散射场强信息即可构建出系统整体的系统函数，并求解输电线路无源干扰的谐振频率。

1 输电线路无源干扰产生机理及其谐振频率求解方法

1.1 输电线路无源干扰产生机理

广域空间下的输电线路输电距离长达几十到几百千米不等，在某些情况下，将不可避免地穿越各类无线电台站信号所覆盖的区域。此时，无线电台站发射的入射电磁波与输电线路金属结构中的带电粒子相互作用，从而在输电线路表面产生与入射电磁波同频的感应电流，使输电线路被动地向附近空间辐射电磁波。该辐射电磁波与原入射电磁波叠加，改变原入射波的幅值和相位，对无线电台站的信号发射或接收产生干扰，即无源干扰。输电线路对无线电台站无源干扰如图1 所示。

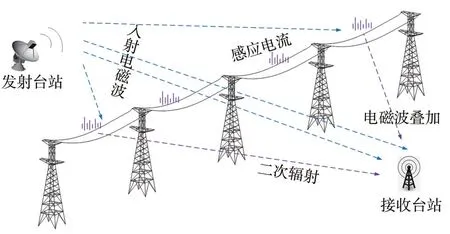
图1 输电线路对无线电台站无源干扰Fig.1 Schematic diagram of passive interference from power transmission lines to radio stations

1.2 现有的谐振频率求解方法

输电线路无源干扰计算主要采用矩量法。计算输电线路无源干扰的简化模型如图2 所示。图中有2 个坐标系，即直角坐标系(x,y,z) 和球坐标系(r,θ,φ)，电磁波Ei以入射角(θi,φi)照射到输电线路上；Es为观测点P处的散射场强。为获取输电线路表面的感应电流，而后获取任意观测点的散射场强，须建立联系输电线路表面感应电流和入射场强之间的电场积分方程。

图2 输电线路无源干扰求解模型Fig.2 Passive interference solution model for power transmission lines

根据电磁场的基本理论，空间任意一点的散射场强可表示为

式中：ω为入射电磁波角频率；μ为磁导率；k=为自由空间的波数，其中，ε 为自由空间的介电常数；∇为哈密顿算子；为格林函数，其中，r'和r分别为源点和场点所在的位置；(r')为感应电流；Sd为输电线路表面积分域。

由理想金属导体表面切向电场为0 的边界条件，可得

式中：“tan”表示取切向分量。

将式（1）代入式（2）可得

式（3）即为联系输电线路表面感应电流与入射电场的电场积分方程，由于式（3）涉及大量积分运算，感应电流(r')的求解过程困难。一般采用矩量法，将输电线路划分为若干单元，即对感应电流作离散处理，从而将式（3）的积分方程转化为矩阵方程。根据每个剖分单元的感应电流在观测点处散射场强的叠加，即可获取任意位置的散射场强Es(r)。

求解干扰极值的过程中，在无线电台站工作频段内，通常先选定若干固定的θi值，而后在［0°，360°］等间隔改变φi取值，从而改变Ei的入射方向，以获取图2 中观测点P处散射场强Es(r)的最大值。显然，此方法为离散化求解，需要进行大量的扫频计算。当入射电磁波频率更高或线路结构更复杂时，消耗的计算资源更多，甚至出现无法求解的情况，且该方法只停留在定性分析无源干扰水平阶段。

2 基于广义谐振的输电线路无源干扰谐振频率求解

2.1 输电线路无源干扰的广义谐振频率及Q值

文献［16-17］在对飞机、船舶等电大尺寸散射体进行研究时，发现在某些特定频率下，存在目标散射体的电磁散射突然增强的现象，将其定义为广义谐振；从传输线理论、广义谐振腔理论等方面对其进行深入研究，推导出广义Foster 定理［18］与广义谐振条件的计算公式。该理论针对的是以线天线为对象的多天线系统在近场区的谐振现象，但可将其理论方法和相关结论发展到同样处于开放空间的输电线路无源干扰谐振频率研究中。

由坡印廷定理可知，对于任意封闭曲面S所包围的空间体积为V的电磁系统，假设其外法线单位向量为，可得系统的复功率平衡表达式为

式中：σ为电导率，为空间函数；α为衰减因子；E为远场区的电场场强；E*为远场区电场场强的共轭；H为远场区的磁场场强；H*为远场区磁场场强的共轭。

考虑输电线路和无线电台站组成的电磁开放系统如图3 所示。图3 中，Sp为第p个天线覆盖区域的表面积，vp为第p个天线覆盖区域表面所包围的区域，N为天线总个数，v'为输电线路表面Sd所包围的区域。

假设输电线路和无线电台站构成封闭曲面Se，曲面Se包含的空间体积为Ve，如图3 所示。在无源区（Sd区），采用坡印廷定理有如下表达式：

在空间无穷远处，即Ve=V∞时，坡印廷矢量虚部为零，则从电磁能量的角度可以认为式（4）和式（5）具有相同的物理含义。因此，可将输电线路金属阵列、无线电台站视为统一整体，引入系统函数的概念，从而应用系统函数的零极点来预测系统的谐振频率。当系统谐振时，式（5）中等式右边最后一项为零。

输电线路构成的金属阵列，可以看作有耗的电磁系统，设其损耗为Ploss，根据复频率理论，引入复频率=ω0(1+jδ)，其中，ω0为系统的谐振频率，δ为损耗因子，根据系统中能量的衰减特征，其损耗为

式中：W为t时刻系统谐振时存储的平均能量。

谐振系统品质因数Q值为

可得

通过以上推导，能够将输电线路无源干扰谐振频率与Q值一一对应起来。根据文献［16］中的结论，当谐振频率所对应得Q值足够大时，输电线路无源干扰才表现出较强的谐振，即干扰水平较高，可据此筛选掉不明显的谐振极点。

2.2 输电线路无源干扰的系统函数及谐振频率求解

上文中，基于广义谐振理论，引入输电线路无源干扰系统函数的概念。假设系统函数为E(s)，并在复频域中展开。

式中：O(s)、I(s)分别为系统函数在复频域对应的输入与输出；E(s)为观测点处的散射场强的复数表示形式，即E(s)=| |Es(r) ejφ(r)，其中，φ(r)为Es(r)对应的相位；a0、a1、a2、…am和b0、b1、b2、…bn分别为将系统函数在复频域用Padé 有理函数展开后分子和分母多项式的系数；s=jωˉ为复频率；m和n分别为系统函数E(s)分子分母的最高次项，决定待求系数a、b数量。上述系数可由模型参数估计［19-20］插值计算方法获得。在MATLAB 中采用roots 函数直接求解系统函数分母多项式的根，即为系统函数对应的极点。其中稳定的极点（在复频域左半部分的极点）对应于输电线路可能的无源干扰谐振频率。

2.3 算例分析

2.3.1 广播天线激励下的无源干扰

基于IEEE 提供的0.535～1.705 MHz 频段广播天线激励的9 基铁塔输电线路的无源干扰模型，本文在电磁仿真软件FEKO 中建立考虑铁塔细节的仿真模型，如图4 所示。其中，输电线路铁塔高为50.9 m，档距为274 m。

图4 输电线路无源干扰仿真模型Fig.4 Simulation model of passive interference for power transmission lines

广播天线高为195 m，距离输电线路中心448 m。天线馈电电压为1 V，位于地面上。仿真频率范围为［0.53 MHz，3.20 MHz］，采样点间隔为0.12 MHz，共有采样点23 个。采用矩量法计算观测点P（0，2 000 m，0）处的场强信息。

根据采样点的场强信息，包括场强幅值和相位，通过模型参数估计插值方法计算式（9）中的系数a0、a1、a2…、am和b0、b1、b2…、bn，从而获取系统函数，并计算其极点。根据广义谐振理论获取谐振频率及Q值。在初步移除不稳定极点后，相关参数如表1 所示。

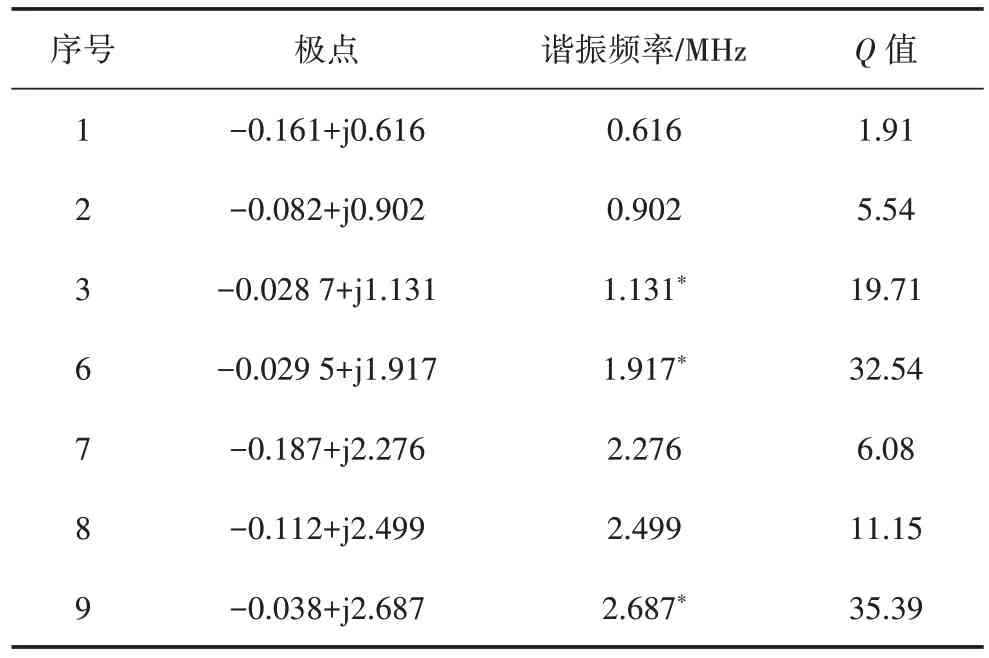
表1 无源干扰谐振频率计算结果Table 1 Calculation results of passive interference under different resonance frequencies

根据广义谐振理论，只有当Q值足够大时，才有较强的谐振特性。因此，可以确定频率为1.131 MHz、1.917 MHz、2.687 MHz，即第3 个、第6 个和第9 个极点对应输电线路的无源干扰谐振频率，如表1 中的“*”所示。

为验证方法的准确性，将本文方法的预测结果与IEEE 模型的预测值进行比较。在考虑地线的情况下，IEEE 谐振频率为［11］

式中：c为光速；h为塔高；d为档距；M为正整数。

在0.535～1.7 MHz 频段内，根据式（10）计算的谐振频率为0.431 MHz、0.862 MHz、1.293 MHz。与表1 中本文方法预测的谐振频率对比，可以发现，在1.7 MHz 以下，本文方法仅在1.131 MHz 时出现干扰谐振，且与IEEE 的预测结果有一定偏差。这可归因于仿真中采用了更精细的模型，并从能量角度消除了不明显的谐振点（即忽略了0.606 MHz 与0.902 MHz 的谐振频率）。

在0.535～3.2 MHz 频带内，本文方法预测的结果与矩量法扫频计算结果如图5 所示。显然，两者的结果一致，第2 个干扰峰值处的最大偏差约为3%。

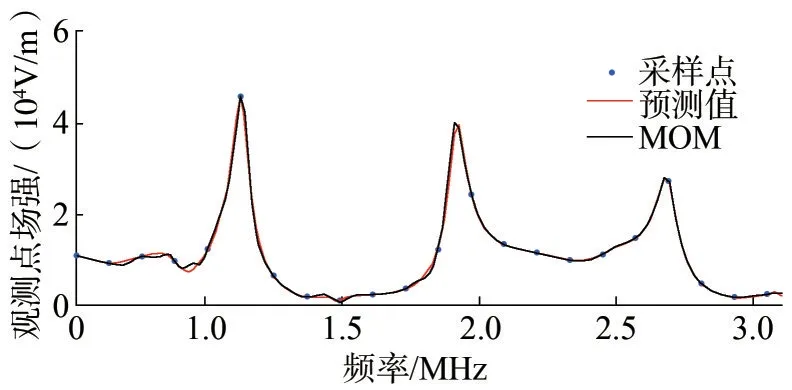
图5 广播天线激励下散射场强Fig.5 Scattering field strength excited by broadcast antenna

为了分析采样点对预测结果的影响，选择17 个采样点，即采样间隔为0.15 MHz，预测无源干扰谐振频率，相关参数如表2 所示。

表2 无源干扰谐振频率计算结果Table 2 Calculation results of passive interference under different resonance frequencies 单位：MHz

与表1 中的计算结果相比，可以发现采样点的变化导致计算结果有一定偏差，但可以保证系统的真实谐振频率不变。因此，通过适当选择采样点，可以较准确地获得无源干扰的谐振频率。

为了更直观地展示输电线路在广播天线照射下的近场分布情况，绘制3 个谐振频率下的输电线路近场云图如图6 所示，绘制3 个非谐振频率下的输电线路近场云图如图7 所示。

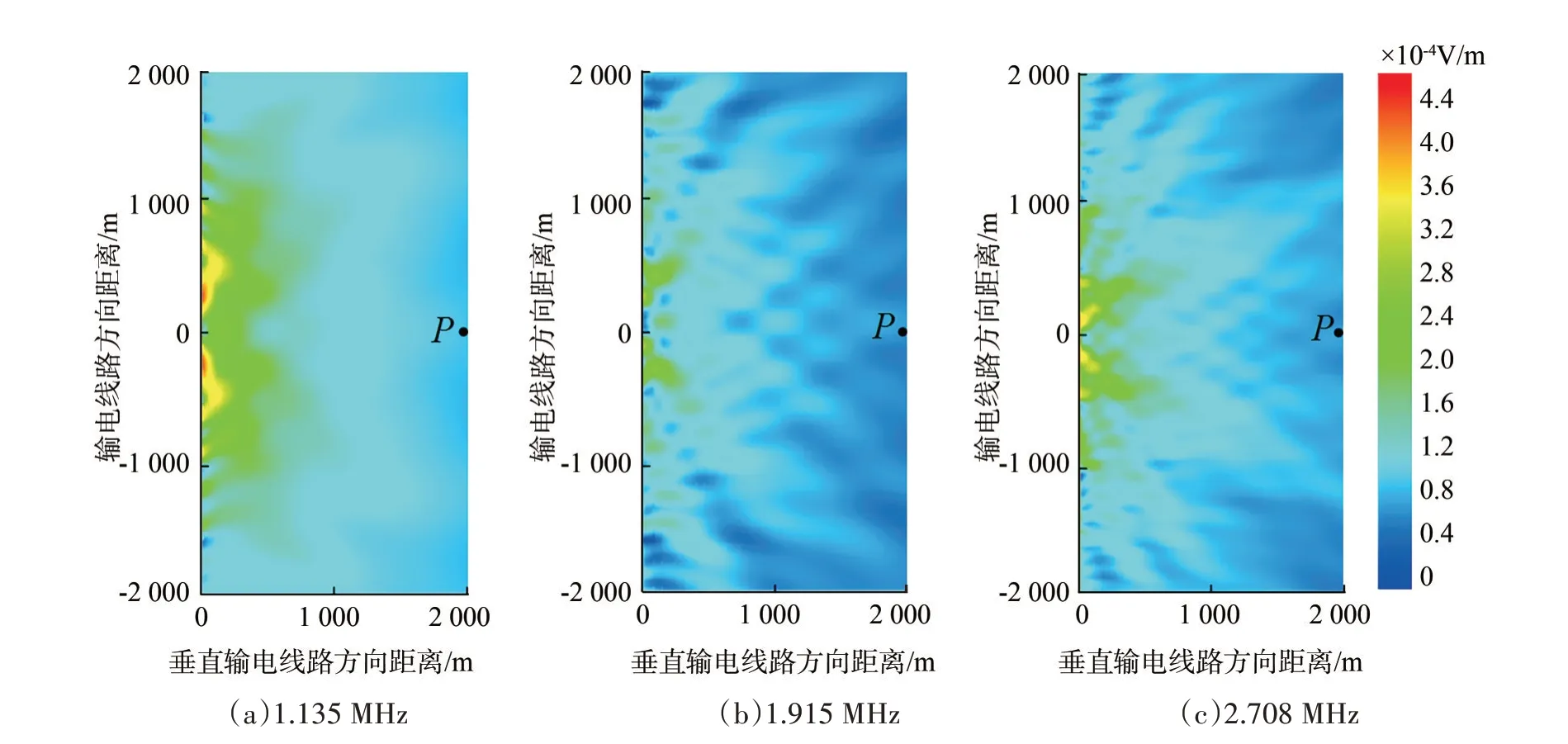
图6 谐振频率下的输电线路近场云图Fig.6 Near-field nephogram of power transmission lines at resonance frequency

图7 非谐振频率下的输电线路近场云图Fig.7 Near-field nephogram of power transmission lines at non-resonant frequency

显然，相同位置处，谐振频率下的散射场强远高于非谐振频率下的散射场强。同时值得注意的是，越靠近输电线路，散射场强越强，即散射场强随空间距离的增加而衰减，该现象可由式（1）解释。文中仿真实验观测点P的位置依据实际情况（输电线路和广播台站的位置关系）选定。因此，本文输电线路无源干扰谐振频率的预测方法准确可行。

2.3.2 垂直极化平面波激励下的无源干扰

为了验证该方法对不同激励的适用性，将图2中的广播天线替换为垂直极化平面波，入射场强为1V/m。可以发现用垂直极化平面波作为激励时，散射场强会有所增大，但不会影响输电线路无源干扰的谐振特性分析。选择Q值较高的前3 个极点，其对应的参数列于表3。当与图8 所示的矩量法结果进行比较时，前2 个谐振频率非常一致。但第3 个谐振频率的偏差约为0.5 MHz。

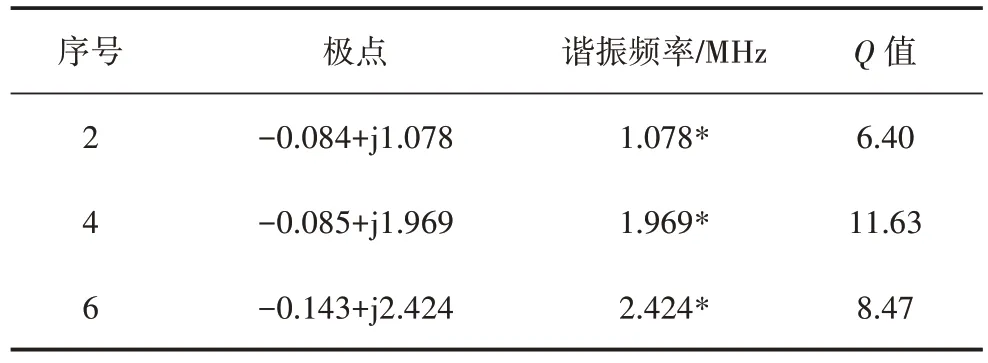
表3 前3个高Q值无源干扰谐振频率Table 3 The first three high Q and resonance frequencies of passive interference

图8 垂直极化平面波激励下散射场强Fig.8 Scattering field strength excited by vertically polarized plane wave

通过仿真分析发现，较大的偏差主要由采样点位置造成。由于本文采用等间隔频率的采样点，不可避免地获得偏离场强峰值场强信息。若存在过多偏离峰值的采样点，将直接导致由式（9）求解得到的系统函数的零极点发生偏移，从而使得预测的谐振频率发生偏差。图8 中，第3 个谐振点恰好位于两个采样点之间）（如紫色虚线框所示的3 个位置），直接导致偏差的出现，而前两个谐振点没有出现类似的情况，因而预测的谐振频率较准确。初步建议应选择更多的采样点，且采样点应尽量靠近场强较高的频点，或者引入自适应的采样方法。

3 结论

1）将广义谐振理论引入到中波段输电线路的无源干扰研究中，提出了基于广义谐振理论的输电线路无源干扰谐振频率求解方法，实现了整个中波频段的输电线路无源干扰预测，弥补了IEEE 标准的频率限制。仿真实验表明，该方法不受外界激励源的限制。当采样点合适时，谐振频率预测的最大偏差约为3%。

2）在获取谐振频率时，十分依赖构建系统函数的采样点的位置和数量。理论上，采样点越多，采样点的位置越靠近真实的干扰极值，构建的系统函数越能反映系统的电磁特性，预测的谐振频率也就越准确。但过多的采样点，同样会带来较大的计算量，且干扰极值实际获取也较为困难。因此，研究自适应的采样方法，从而优化系统函数的构建，最终实现跟准确的无源干扰谐振频率预测是下一步研究的重点。