基于改进RRT算法的路径规划研究*
韩金利
(山西机电职业技术学院 数控工程系,山西 长治 046011)
0 引言
路径规划是机器人智能化研究的重要方向之一,多年来,学者们对路径规划算法进行了很多探索。其中RRT(Rapidly Exploring Random Tree,快速扩展随机树)算法具有搜索能力强、算法简单等特点,但是它也有冗余多等缺点,因此许多学者对RRT算法进行了优化。栾添添等[1]提出了以生成的新节点与终点的距离来判断自己所处的采样区域,但距离公式计算效率较低。陈娟等[2]提出了候选点集策略,点集中的数据随机性大。赵文龙等[3]提出了在均匀采样得到的随机点与目标点的连线上随机取一个点作为新的随机点进行树的扩展,但没有考虑到在障碍物附近新节点的生成问题。张恩东[4]提出了一次采样多次扩展的方式,没有对采样点重复利用。董璐等[5]提出了历史路径缓存池概念,没有对历史路径中的节点进行筛选。
针对以上问题,本文提出了基于改进RRT算法的路径规划。以地图长、宽进行分区,利用新节点的坐标值判断处于何种分区,并将首先进入最新区域的节点作为根节点,向着目标扩展,使得算法随机性减弱,转折点更少。
1 基本RRT算法
RRT算法的基本思想是:随机点决定节点的扩展方向,扩展步长决定扩展速度。对问题定义如下:
假设C为探索空间,在探索空间中有自由空间qfree与障碍物空间qobs,并且qobs⊂C,qfree⊂C;探索空间中的起始点为qstart,qstart∈qfree,目标点为qgoal,qgoal∈qfree,qrand为随机点。随机点qrand初始路径生长过程如图1所示。
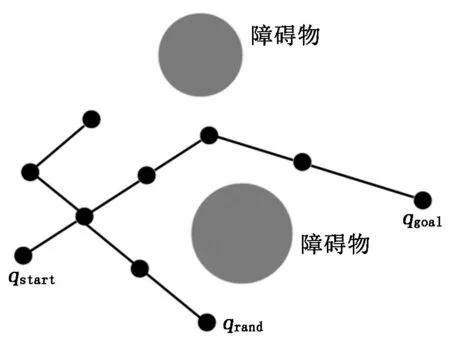
图1 qrand初始路径生长过程
2 改进RRT算法
2.1 节点扩展策略
这里采用进五取二的策略,当随机数大于阈值时,节点扩展步长数为1,当小于阈值时,节点扩展步长数为5;在扩展过程中,若遇到障碍物,则停止扩展,否则则扩展5步。这里采用前进5步,只将其中的两个节点加入随机树中,这里取第2步节点和第5步节点加入随机树中。
2.2 最近点分区搜索策略
根据地图大小及目标点与开始点之间的距离划分随机树扩展区域,只要一个新节点首次进入下一区域,就以进入该区域的最新点为根节点,并且在区域范围内生成随机树,将最近点搜索限制在区域范围内,缩短搜索时间,一定程度上加快了可行路径的生成。
2.3 随机点分区采样
根据起点与终点位置,将地图分为3个区域,用虚线表示分界线,这里将一区、二区随机点采样区域指定为整个地图,三区采样空间指定为二区和三区,既保证了随机树一定程度上可反向扩展,又保证了随机点的选取使得随机树可向目标点扩展,最大程度上避免随机树刚刚进入新的区域时容易陷入局部震荡。随机采样分区扩展示意图如图2所示。
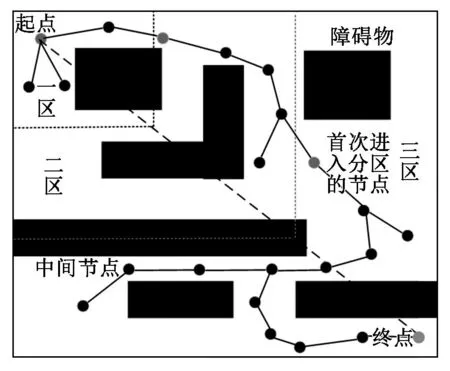
图2 随机采样分区扩展示意图
2.4 节点试采样回退策略
在分区采样的过程中,提出了一种在扩展树生长初期有限进入已探索区域的有限回退策略,即节点试采样回退策略。设置一个标志位,当节点采样生成新节点未通过碰撞检测1次则加1,当采样点生成新节点通过检测,且新节点又在重复采样分区则标志位减1,直到标志位数值达到阈值K,则允许重复采样分区新生成的节点加入到随机树。
2.5 逆向剪枝与路径平滑
改进RRT算法能够迅速找到初始路径,但生成了很多冗余节点,这里对初始路径的节点集合进行剪枝操作,逆向剪枝示意图如图3所示。图3中,黑色方块为障碍物,实线为原始路径,点划线为碰撞检测连线,虚线表示中间省略有很多节点。
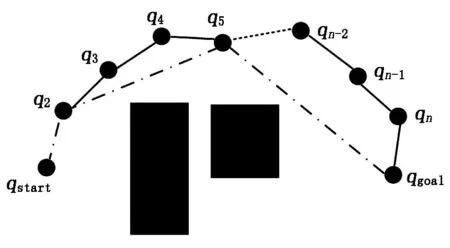
图3 逆向剪枝示意图
路径平滑采用二次贝塞尔曲线进行拟合处理。在路径中选择连续的3个节点qi-1,qi,qi+1,中间节点与前后两个节点连线上选择固定距离smooth_dis,并保证该距离不会超过两条边的中点。贝塞尔曲线拟合示意图如图4所示。其中,p0、p1、p2为拟合曲线上的3个点。
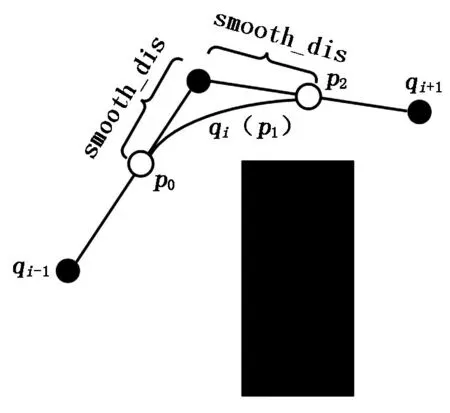
图4 贝塞尔曲线拟合示意图
3 实验与分析
为了验证本文改进算法的优良性能,将本文算法与基本RRT算法和偏置RRT算法进行对比实验。由于RRT具有随机性,这里设置实验次数为20次,各种算法指标求平均值,为保证算法验证的客观性。三种算法原始路径如图5所示,三种算法实验结果如表1所示,本文算法路径优化效果及成本变化如图6所示。
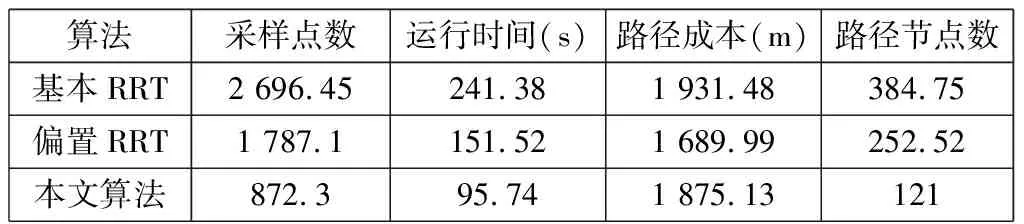
表1 三种算法实验结果

图5 三种算法原始路径
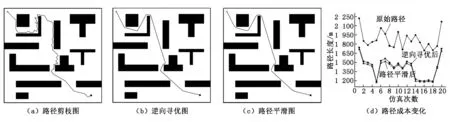
图6 本文算法路径优化效果及成本变化
从表1可以看出:三种算法的路径成本相差不大,在采样点数、运行时间、路径节点数等指标方面本文算法优势十分明显;本文算法相较于基本RRT算法采样点数减少了67.65%,相较于偏置RRT算法采样点数减少了51.19%;本文算法运行时间相较于基本RRT算法减少了60.34%,相较于偏置RRT算法减少了36.81%;本文算法路径节点数相较于基本RRT算法减少了68.55%,相较于偏置RRT算法减少了52.08%。
由图6可知:原始路径平均长度为1 875.13 m,逆向寻优后路径平均长度为1 424.85 m,平滑后路径平均长度为1 398.48 m,最终路径平均长度减少25.42%。由此看出,经过拟合处理后,拟合路径更加适合机器人运行。
4 总结
本文提出了分区采样RRT算法,对探索空间进行分区,仅在所在区域内寻找最近点,提高了最近点的搜索效率;以进入下一区域的首个节点为根节点,开始在区域中进行探索,最大程度地避免在已采样区域进行重复采样;最终路径由各个分区的搜索树拼接而成。本文算法寻找可行路径速度更快、节点更少、效率更高、导向性更强。

