面向极限生存能力提升的城市配电网反脆弱规划方法
时珊珊,张琪祁,魏新迟,刘晋萍,王颖,许寅
(1.国网上海市电力公司,上海市 200437;2.北京交通大学电气工程学院,北京市 100044)
0 引 言
近年来,全球发生了多起因极端事件导致的大停电事故,如2019年纽约停电事件、2021年的得州停电以及2022年台湾省大面积停电等,带来了巨大损失。而城市电网内部负荷密度高、重要负荷多,一旦停电损失难以估量,提升城市配电网的韧性迫在眉睫。我国住建部和发改委2022年7月发布《城市基础设施十四五规划》中明确提出要“开展城市韧性电网和智慧电网建设”;同时国家能源局发布的《坚强局部电网规划建设实施方案》和国家发改委发布的“十四五规划”中均要求在城市重点区域布局建设“结构清晰、局部坚韧、快速恢复”的坚强局部电网,为城市电网韧性提升提供政策支持。
通过在规划阶段布置可控分布式电源、储能或对线路进行差异化加固/升级有助于从源头上为电网应对极端事件提供源-网等资源基础,保障重要负荷实现极限生存,提升电网韧性[1]。反脆弱规划的原理,即在规划阶段将资源分散化布置,虽然可能牺牲一定经济性,但能够确保系统在高度不确定的极端场景下通过非计划孤岛运行保障本地重要负荷极限生存,降低潜在的停电损失[2-3],提升配电网反脆弱能力。
近年来,国内外学者在配电网韧性规划领域已开展了一定研究。规划措施主要包括新增分布式电源(distributed generation,DG)、加固/新增线路等措施。文献[4]考虑加固线路的措施,采用分布式鲁棒优化以最小化线路加固投资及最坏情况下的切负荷损失为目标建立模型。文献[5]针对电网应对台风灾害的韧性提出大电网规划方法,考虑N-k故障,采取两阶段鲁棒defender-attacker-defender模型,对规划问题进行建模和求解。文献[6]提出了一种基于信息间隙决策理论(information gap decision theory,IGDT)的决策策略,进行了DG分配和加固/新增线路两种措施的权衡,以便配电系统规划人员面对极端事件做出规划。文献[7-8]将面向韧性提升的配电系统规划转化为两阶段随机混合整数规划问题。然而,该研究规划过程只考虑分布式电源的位置选取,通常假设所有电源的容量相同[7]。在某些N-k故障情况下,若干个具有相同容量的电源处于最佳位置,但在某些非计划孤岛中其容量不足,而在其他非计划孤岛中容量过剩。因此,在规划中应同时考虑DG的最佳分布位置和容量大小。文献[9]提出了一种新的两阶段随机混合整数线性规划模型来应对自然灾害的不确定性,并且提出了一种选择线路故障场景的方法。文献[10]提出了一种有效的规划策略,用于加固台风作用下的配电系统线路。该框架不仅考虑了线路加固的技术效益,还考虑了停电造成的经济损失成本,为配电系统的可靠性提供了重要参考。国内针对坚强的局部电网韧性规划领域,提出了一些相关概念,其中包括保底电网等。文献[11]认为保底电网是指电网为了应对严重自然灾害,选取电网的重要节点、关键线路和保障电源进行差异化建设形成最小规模网架,以保证重要负荷供电,最小化故障范围,提高城市核心区域和重要电力用户供电安全,提高电网快速恢复供电能力。文献[11-12]提出了一种差异化规划建设的防风保底电网构建方法,选取城市重要站点和关键线路构建最小规模的防风保底电网,并提出多项评价指标评估所构建的保底电网,以提高沿海地区电网防风抗灾能力。文献[13]提出了一种城市防风抗灾保底电网的多目标规划模型,以最小化保底电网规模和优先采用电缆线路为联合优化目标。上述研究中电网规划方案所考虑的规划措施较为单一,统筹考虑不同的规划措施类型,包括线路差异化规划和分布式电源布点定容等,有助于充分发挥源侧-网侧各类资源的韧性提升潜力,最大化提升系统极限生存能力。文献[14]提出了一种计及预防阶段、抵抗-响应阶段、恢复阶段的多阶段协同弹性提升策略。通过实际运行曲线与理想运行曲线之差量化电网弹性,实现城市受端电网弹性评估。弹性提升模型以投资运行总成本最小和电网弹性最大为目标,包含输电通道加固、机组组合以及增加修复队伍3种措施,涵盖台风过境电网3个阶段状态变化。文献[15]针对极端台风灾害下电网韧性评估及差异化规划方法展开研究,该文章首先提出了一种考虑重要负荷供电韧性评估指标,然后构建了差异化规划的两阶段优化模型。文献[16]研究了极端天气对元件故障率的影响,并建立了数学模型来反映台风风速与故障率之间的关系。研究还构建了韧性评估方法,比较了传统加固元件与接入分布式电源两种措施对韧性的提升效果,并验证了提出方法的有效性和准确性。
本文结合城市电网空间限制因素,考虑我国沿海城市可能遭遇的台风灾害,统筹考虑线路差异化加固/升级措施和DG布点定容措施,提出两步骤规划思路。其中,第一步确定候选线路规划方案集合,第二步针对每个线路规划方案确定DG布点定容规划方案,最终得到整体规划方案。其中第二步中,统筹考虑规划投资阶段和运行阶段极限生存的目标和约束条件等,将DG布点定容问题建立为混合整数线性规划模型,均衡经济性和极限生存能力提升需求。
1 问题描述及规划框架
1.1 城市配电网反脆弱规划问题描述
城市配电网负荷密度高、供电可靠性要求高。为了提高重要负荷的极限生存能力,需要在规划阶段选择关键线路加固/升级、在关键节点布置相应容量的DG,确保在极端事件作用下,保住关键线路不受损,从而保障极端情况下本地DG通过未受损的线路为重要负荷不间断供电,实现重要负荷极限生存,如图1所示。
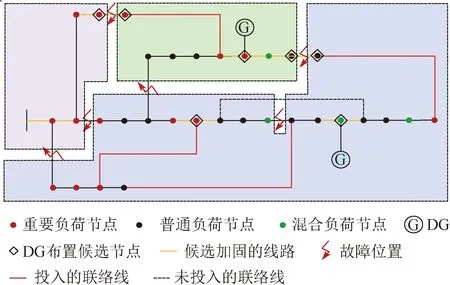
图1 配电网实现极限生存的孤岛运行状态Fig.1 The distribution network realizes the island operation state of extreme survival
本文研究对象为台风灾害下的城市配电网,并作出如下假设:
1)配电网内部包含常开联络线,在应急场景下可以通过远程控制实现开关状态控制[17];
2)配电网内部包含若干重要负荷节点(critical loads,CLs),如医院、地铁、通信基站等,普通负荷节点(interruptible loads,ILs)如街道照明、居民负荷、游乐场等以及混合负荷节点(既接有重要负荷也接有普通负荷);
3)考虑到城市内部空间限制因素,不考虑新增线路措施,仅考虑线路加固/升级措施(如架空线入地等);
4)待安装的DG均为柴油机,通常会建造专用的发电厂房或机房。这些厂房或机房根据设备的规模和特点进行设计,提供必要的空间和结构支持,以容纳发电设备和其他配套设备,确保设备的正常运行、尽量不受外部环境的影响。因此,假设可控分布式电源在极端天气灾害下不会受台风影响而发生故障停止供电[18]。
本文考虑的配电网反脆弱规划,以均衡投资经济性和极限生存能力提升效果为目标,考虑的约束条件包括预算限制、极端场景下极限生存相关的各类约束等。
1.2 两步骤反脆弱规划框架
本文提出了城市配电网两步骤反脆弱规划的框架,如图2所示。第一步基于启发式方法,结合线路规划预算限制以及网络连通度等指标,确定候选线路加固/升级方案集合;第二步基于随机规划理论,确定不同线路加固/升级方案下的最优DG布点定容方案,最终通过经济性和极限生存能力比选,得到最终的规划方案。
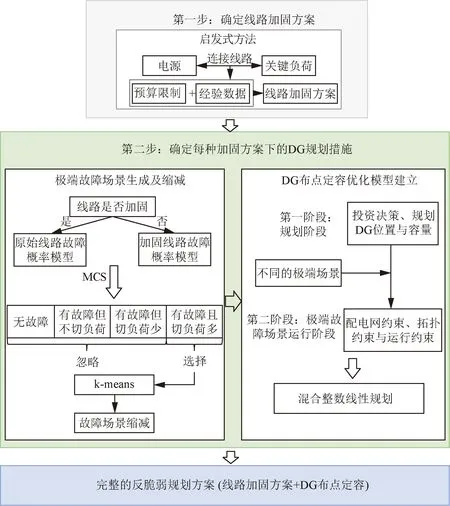
图2 配电系统韧性规划框架Fig.2 Distribution system resilience planning framework
其中,第一步主要基于启发式方法确定候选线路加固/升级方案集合,第二步考虑了极端场景的高度不确定性,提出了代表性极端场景生成和削减方法,并进一步提出了DG布点定容的两阶段规划模型。下面将主要针对第二步中极端场景生成削减方法和DG布点定容的两阶段规划模型进行阐述。
2 考虑台风灾害的极端故障场景生成及代表性场景筛选方法
由于配电网在台风灾害中的故障情况受多种因素的影响,将所有线路的运行状态排列组合可以得出2m种故障场景,其中m为配电网中线路条数。对于复杂网络来说,在优化模型构建时将所有可能出现的故障场景都考虑进来是不切实际的。因此,在建模之前需要选出一组有代表性的极端故障场景。
采用抽样平均近似方法(sampling average approximation method,SAA)实现以上目标[19]。抽样平均近似方法是用抽样的方法将随机变量用样本表示,从而将随机规划问题转化为确定性问题[20]。那么原问题可以写为:
(1)
式中:n为抽样的次数或者样本的大小;ξ为随机变量;x为决策变量,SAA可以采取抽样的方法用样本ξi表示随机变量。
2.1 线路故障模型
本文采用从“NaFIRS”数据库中导出的概率故障模型[21]。该数据库记录了从2003年到2010年由台风引起的约1.2万起配电系统故障。线路故障概率拟合曲线为:
pij=αLijvβ
(2)
式中:Lij为线路长度;pij为线路故障概率;v为台风风速;α、β为常数。在城市配电网中,常数α、β分别取值为:α=2×10-17km-1、β=9.91。
据文献[21]数据显示,大陆地区的台风风速很少会超过42 m/s。此外,根据美国历史数据库的报道,台风登陆后的最大风速通常在36~42 m/s之间,最大风速可能在农村地区或城市地区随机出现,不受地理位置的限制。这些数据表明,台风的风速在一定的范围内波动,且通常不会超过42 m/s,但可能因地理因素而有所不同。结合本文内容分析讨论,认为城市电网所遭受的台风风速为38 m/s左右。
2.2 基于蒙特卡洛模拟的故障场景生成
蒙特卡洛模拟方法(Monte Carlo simulation method,MCS)依赖于大数定律,随着样本数量增加,随机样本的统计特性趋于真实的概率分布。在上述分析的基础上,本文提出了一种基于MCS的场景生成方法(算法1),如表1所示,算法中N表示生成的场景总数,U(0,1)表示产生一个随机数,且服从0到1之间的均匀分布,用该随机数与某一事件发生的概率大小相比较来模拟事件是否发生。

表1 基于MCS的场景生成方法Table 1 Scenario generation method based on MCS
初步筛选场景的方法主要由以下2个标准来确定:
1)通常,两阶段随机混合整数规划所需要的场景数量至少应该为50[7],数量的场景太少无法充分表示问题的不确定性,以至于最终的决策结果不准确。
2)重要负荷切负荷量一旦超过总负荷量的10%,并且故障线路数量超过了ntie-1条,其中ntie表示联络线的条数,意味着在这种情况下,系统已经达到了较为极端的负荷状态,配电网将被划分成多个孤岛。这种情况下,系统可能会面临非常复杂和严峻的工况,可能导致严重事故的发生。
初步筛选场景前,需要得到所有被切除的节点集合,可以使用其他的算法,如深度优先或广度优先。这2种算法是常用的图搜索算法,用于在图或树等数据结构中搜索或遍历节点,适用于具有辐射网状拓扑结构的配电系统中。从源节点开始遍历后,将访问从该节点可以到达的所有节点。算法1中详细说明了故障场景的生成与初筛的求解思路。
2.3 基于K-means聚类的故障场景筛选
在传统方法中,可以使用K-means聚类方法对具有相似负荷/风廓线的场景进行合并[22],从而实现对电力系统或风电场的负荷/风能资源进行分析。
在算法1生成的场景中,可能存在一些重复的随机场景。这些重复的场景有2种情况:一是故障位置完全相同;二是故障位置不同,但故障节点所带负荷量相同,因此总的切负荷量相同,如图3所示。因此,可以从这些重复的场景中选一个具有代表性的场景来表示这一类。

图3 相似故障场景示例Fig.3 Example of similar fault scenarios
K-means算法的核心思想是不断地进行迭代将样本分配到k个簇中,并更新簇中心,直到簇中心收敛或达到预定的迭代次数。假定有s个样本数据S={N1,N2,N3,…,Ns},其中每个样本数据都有n个维度的属性。经过聚类分析后每个数据都会被分配到一个簇内,每个簇都对应一个簇中心,簇中心记为{C1,C2,C3,…,Ck},0≤k≤s。通过计算比较每一个数据与每一个簇中心(质心)的距离,计算公式如式(3),将数据分配到距离质心最近的簇内,得到k类簇L={L1,L2,L3,…,Lk}。
(3)
式中:Su表示第u个样本数据,1≤u≤s;Cv表示第v个簇的中心,1≤v≤k;Suw表示第u个样本数据的第w个属性,1≤w≤n;Cvw表示第v个簇质心的第w个属性,1≤w≤n。
在上述分析的基础上,采用肘部法则确定聚类数目k。肘部法则在K-means聚类分析中的作用是帮助选择最优的聚类数目,避免出现由于k值的选择不当而导致聚类效果不佳[23]。该法则的核心依据是各个簇内部的数据点到其所属簇中心点(质心)的距离的平方和(sum of squared errors,SSE),将不同的k值对应的SSE绘制成图表,横轴表示k值,纵轴表示对应的SSE。随着k值的增加,SSE通常会逐渐减小,因为更多的聚类中心可以更好地拟合数据,降低了每个数据点与其所属聚类中心之间的距离。根据肘部法则,该曲线的拐点对应的k值被认为是最优的聚类中心数目。在该取值下,聚类的效果较好,并且在继续增加k值时,聚类性能提升缓慢,不再与增加的计算成本和复杂性相匹配。
3 面向极限生存能力提升的城市电网规划优化模型构建
3.1 第一阶段模型:规划阶段模型
在优化模型的第一阶段中,主要考虑预算限制。这一阶段的目标是在给定的资金预算下,确定由随机极端事件所导致的故障状态下的最佳DG分布情况,同时要保证预期运行成本最小化。
3.1.1 目标函数
(4)

目标函数式(4)由两部分构成,分别为投资成本和在随机故障场景下故障后的极限生存能力,该目标函数中的决策变量为DG的位置分布及其容量大小。
3.1.2 约束条件
(5)
(6)
(7)
(8)
(9)

3.2 第二阶段模型:极限场景运行模型
第二阶段为极限场景下的运行模型,目标为最大化极限生存能力,本文中极限生存能力用保障加权负荷不间断供电量来表示,考虑相关的运行约束、辐射状拓扑约束等。
3.2.1 目标函数

(10)

在故障场景s∈S下,目标函数表示为式(10),该函数由极端故障场景下保证供电的负荷收益构成。
值得说明的是,对于城市电网来说,不同季节下城市负荷类型的占比不同,在应用此方法到实际城市电网中时,需要收集该城市不同季节下负荷类型占比情况信息,将四季情况考虑到子运行模型中,从而使求解结果更加符合实际情况。
3.2.2 约束条件
1) 辐射网状拓扑约束。
鬼子军官用手指了指周教授几个,又在空中划个圈儿,哇啦哇啦说了句什么,几个日本兵一齐弯腰嗨了声,哗啦啦散开站成一圈儿,用枪剌抵住周教授几个。
(11)
(12)
-Myij≤Fij≤Myij,∀(i,j)∈ΦB
(13)
yij=0,∀(i,j)∈ΦF
(14)
式中:yij为线路状态,线路闭合时其值为1,线路断开则为0;N为配电网节点总数;约束中断Fij可看作连续变量,用于表示线路(i,j)流过的虚拟流大小;ΦG、ΦB、ΦF分别表示源节点集合、线路集合、因故障断开的线路集合;β(j)、α(j)分别表示节点j的子节点、父节点;M为一个很大的正实数,用于“大M法”。
对配电网拓扑重构后形成的每一个孤岛都要遵循式(11)—(14)的约束条件,充分保证每一个孤岛都是辐射状的拓扑。约束式(14)表示故障线路被自动开关跳闸,并保持断开状态直到修复。
2) 配电系统运行约束。
该部分约束条件中的变量均为与场景s有关的时变变量,简洁起见,下式中将每条约束的∀s∈S与∀t∈T省略。
(1)DG约束。
(15)
(16)
(17)
约束式(15)—(17)为DG约束。其中,约束式(15)表示发电机组输出功率限制,当节点i没有安装发电机时,该节点的发电机输出功率为0。约束式(16)表示每个待规划发电机的能量可以在短时间内保持稳定供电,等待进一步调度。约束式(17)表示DG的能量限制。
(2)节点负荷约束。
(18)
(19)
(20)
(21)
(22)
(23)

约束式(18)—(23)为节点所带负荷的约束。其中,约束式(18)表示故障后通过拓扑重构和分布式发电机保证供电的负荷量不超过总负荷量。为了简便计算,假设负荷功率因数恒定,采用了参数ξi,见式(19),用于表示有功与无功的比值。因此,保证供电的无功负荷量可以直接用有功负荷量来表示,如式(20)。式(21)—(23)为ILs的剩余负荷约束,与CLs采取相同的约束方式。
(3)潮流约束。
(24)
(25)
(26)
(27)

(28)
-Myij,s≤Pij,t,s≤Myij,s,∀(i,j)∈ΦB
(29)
-Myij,s≤Qij,t,s≤Myij,s,∀(i,j)∈ΦB
(30)
(31)
V1,t,s=Vtran,t,s
(32)
Vtran,t,s≈Vtran0+KTPtran,t,s
(33)

约束式(24)—(33)为网络潮流约束。其中,式(24)、(25)基于待规划发电机发出的无功功率为0这一前提,表示节点注入功率的约束条件。约束式(26)、(27)表示每个节点的功率平衡状态。约束(28)表示线路的电压降,当线路状态yij,s=1,即线路闭合时,该不等式变为等式,按照电力系统线路压降公式计算压降。当线路状态yij,s=0,即线路断开时,该约束失效。式(29)、(30)用于确保线路断开时无功率流过。约束式(31)是配电系统节点电压约束,电力系统的电压波动限制在合理的范围内非常重要,对电力设备的安全运行、保证用户的正常用电和电力系统的稳定运行都具有直接影响。节点1看作变电站节点,该点电压由式(32)给出。如果只有一条线路连接到变压器,则Psub,t,s=P12,t,s,将电压函数近似线性化为式(33)[25]。
(4)线路热极限约束。
(34)
-Sijmax≤Pij,t,s≤Sijmax,∀(i,j)∈ΦB
(35)
(36)
式中:Sijmax为线路的热极限。

配电网中DG布点定容规划的混合整数线性规划模型构建完毕。需要说明的是,本文在建立成本模型式(7)、变电站电压模型式(33)和潮流模型式(34)—(36)时采用了一定的线性化手段,会引入一定的误差。三类线性化手段分别参考了相应的文献,根据文献表述,引入的误差对每个极端场景下极限生存运行结果的影响是可控的,进而对宏观规划方案结果的影响也非常小,可忽略不计。
4 算例分析
4.1 IEEE 33节点算例信息
算例测试基于IEEE 33节点配电系统测试模型开展。相关测试环境为AMD Ryzen 7 4800U处理器(1.80 GHz)和16 GB RAM的笔记本电脑,基于Julia语言实现,并调用Gurobi商业求解器进行求解。
IEEE 33节点配电系统拓扑如图4所示,节点8、14、24、25、30、32、33为DG待布点位置,线路1-2、2-3、7-8、8-9、13-14、14-15、23-24、24-25、29-30、30-31、31-32、32-33为待加固线路集合。
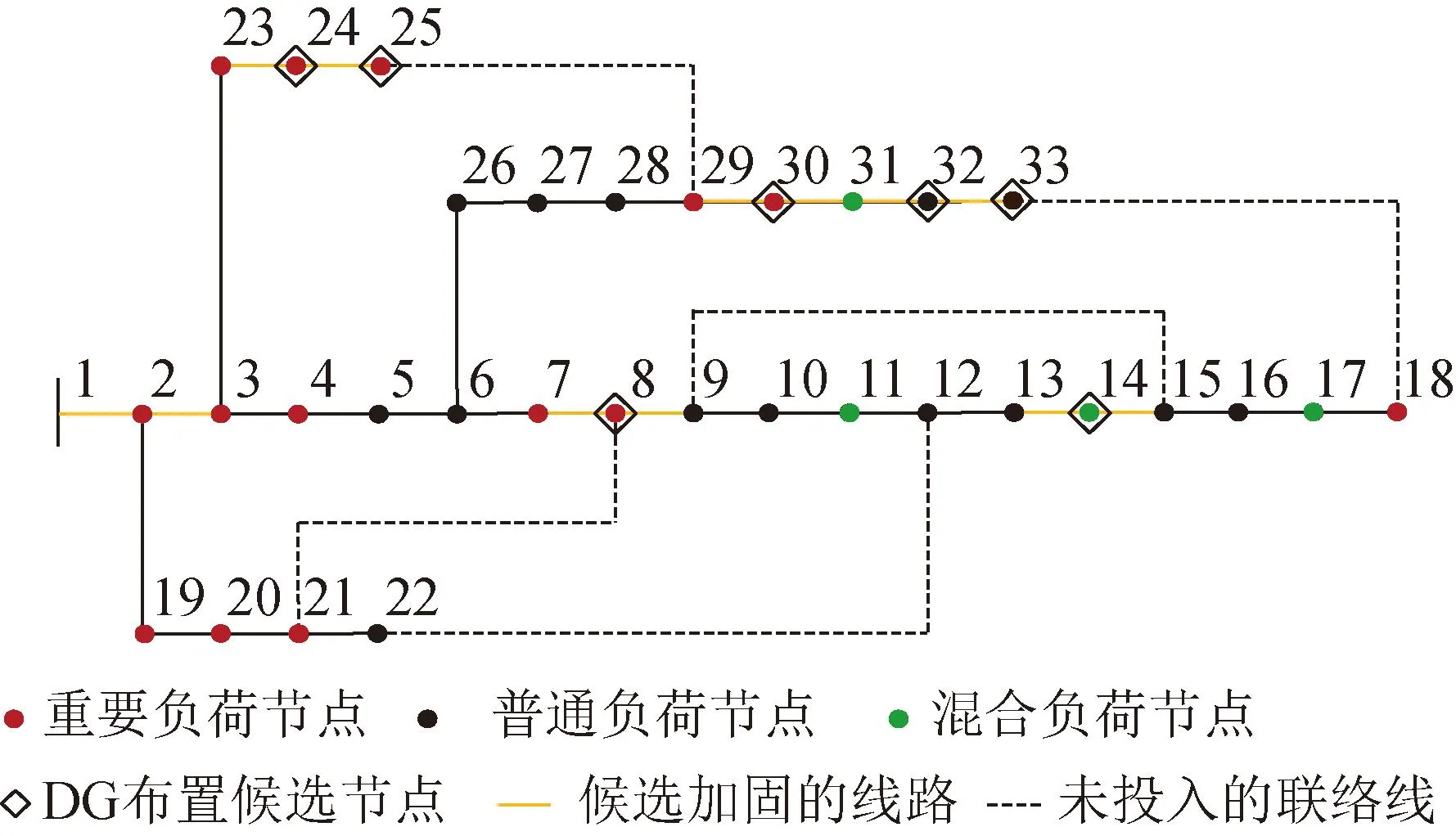
图4 IEEE 33节点配电网模型Fig.4 IEEE 33-node distribution network model
取功率基准值为1 000 kV·A,电压基准值为12.66 kV。本测试基于一组反映负荷变化的数据集[27],其变化曲线如附录图A1所示。
4.1.1 算例测试结果
1)线路加固备选方案。
首先寻找配电网中所有电源节点(包括变电站节点和DG候选电源布置节点)到重要负荷节点(包括重要负荷节点和混合节点)的通路。综合考虑以下两方面来确定关键线路。首先,考虑通路经过次数较多的线路,因为经过次数多意味着该线路在电网中扮演着更重要的角色。其次,考虑重要负荷的保供权和线路负载率。当线路连接着重要负荷,并且具有较高的负载率时,表明该线路具有显著的关键性。由于预算限制,最多可以加固3条线路。因此,本文讨论了以下4种不同的加固线路方案下的优化结果,分别为:
方案1:加固线路14-15、24-25、30-31;
方案2:加固线路1-2、13-14、32-33;
方案3:加固线路7-8、13-14、23-24;
方案4:加固线路1-2、7-8、24-25。
对于这4种加固线路投资相同的方案,要选出能通过布置DG使得系统极限生存能力最强的一种方案。
2)DG布点定容结果。
(1)极端场景生成结果。
以加固线路方案1为例,即加固线路14-15、24-25、30-31的情况下进行极端场景生成结果展示。基于算法1,初步生成了10 000个故障场景,在这10 000个场景中经过切负荷量与断线数量初步筛选后依据K-means聚类分析原理将筛选出的场景聚成k类,k的值由肘部法则确定。在不同的k值下,聚类结果的SSE变化情况如附录图A2所示。
结果表明,当k=2时,SSE很大,元素距离簇中心距离较分散,欠拟合了数据,无法捕捉到数据中的复杂结构和变化模式,造成较大的聚类误差;当k≥3后,SSE下降趋势缓慢,过多的聚类数目会过拟合数据,导致模型过于复杂,在训练数据上表现良好,但泛化到新数据上的性能较差。因此,根据肘部法则,拐点k=3是一个合适的值,将场景聚成3类可以保证较小的误差。
聚类的情况如附录图A3所示,将所得的3类故障场景选出具有代表性的一个场景作为代表,类别1中共有20个相似场景,类别2中共有8个相似场景,类别3中共有24个相似场景。
(2)不同线路加固方案下DG规划结果。
为得到在每种线路加固方案下相应的电源配置情况,对优化模型进行求解,计算时长为1 min。对上述4种方案分别求解,得到的优化结果如表2所示。
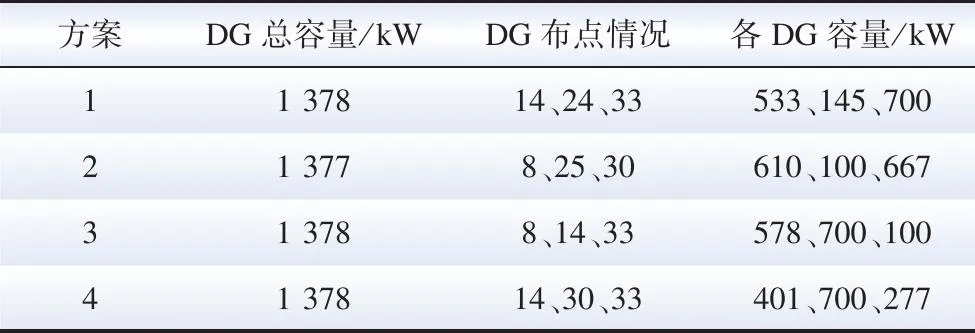
表2 IEEE 33节点算例在不同线路加固方案下的DG布点定容分布结果Table 2 The DG planning results of IEEE 33-node system under different line reinforcement schemes
对所得的优化结果从极限生存能力与总投资的角度进行进一步分析。由表2可知,每种方案的DG总容量相同,因此其布置DG的投资也相同。分别将上述方案的极限生存能力,即第二阶段的目标函数值与无DG安装时的数值对比,如图5所示,方案2对配电网极限生存能力提升的效果最佳。

图5 IEEE 33节点算例在不同方案下的极限生存能力Fig.5 The ultimate survivability of IEEE 33-node system under different schemes
综上,在相同的资金投入下,方案2的优化效果最好。因此选定方案2,即加固线路1-2、13-14、32-33,DG部署在节点8、25、30处,容量分别为610、100、667 kW,规划结果如图6所示。

图6 规划后的配电网Fig.6 Distribution network after planning
图7展示了方案2下发生极端事故时配电网以孤岛运行方式保证供电的极限生存状态。在该场景下,通过拓扑重构与DG共同作用,形成了2个由DG维持供电的孤岛。其中,机组出力为:P8=604 kW,Q8=304 kvar,P30=552 kW,Q30=648 kvar。负荷恢复情况如表3所示。
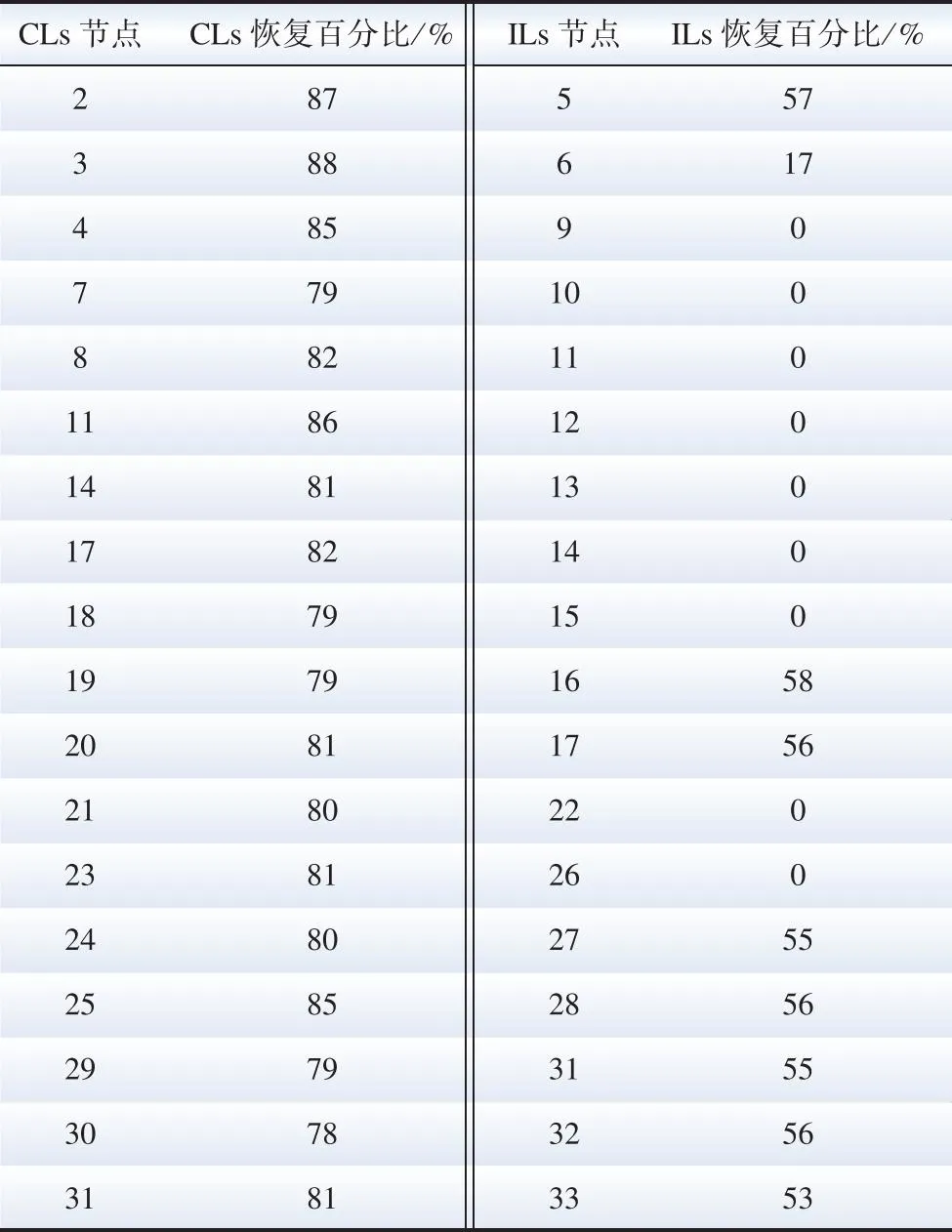
表3 负荷恢复情况Table 3 Load restoration status

图7 规划后的配电网极限生存运行状态Fig.7 Survival operation state of the distribution network after planning
4.1.2 不同预算限制下规划方案对比
图8显示了当采用同一种线路加固方案时,不同预算上限所对应的极限生存能力。其中横坐标为布置DG预算限制,纵坐标为该预算下对应的配电网极限生存能力。

图8 不同预算限制下的配电网极限生存能力变化曲线Fig.8 Variation curve of extreme survival capacity of distribution network under different budget constraints
4.2 IEEE 123节点算例信息
算例测试基于IEEE 123节点配电系统测试模型开展。相关测试环境为AMD Ryzen 7 4800U处理器(1.80 GHz)和16 GB RAM的笔记本电脑,基于Julia语言实现,并调用Gurobi商业求解器进行求解。
IEEE 123节点配电系统拓扑见附录图A4,节点24、48、49、65、76、87、101、108为DG待布点位置,线路1-3、1-7、23-24、47-48、47-49、49-50、50-51、64-65、65-66、67-72、72-76、76-77、76-86、86-87、87-89、101-102、101-105、105-108、108-109、109-110为候选加固线路。
取功率基准值为1 000 kV·A,电压基准值为2.4 kV。
1)线路加固备选方案。
线路加固方案确定原理同上。由于预算限制,最多可以加固5条线路。本文讨论了以下4种不同的加固线路方案下的优化结果,分别为:
方案5:加固线路1-3、23-24、64-65、86-87、101-102;
方案6:加固线路1-7、47-48、72-76、101-102、108-109;
方案7:加固线路1-3、1-7、47-49、72-76、101-102;
方案8:加固线路23-24、47-48、72-76、87-89、101-102。
对于这4种加固线路投资相同的方案,要选出能通过布置DG使得系统极限生存能力最强的1种方案。
2)DG布点定容结果。
(1)极端场景生成结果。
以方案1为例,根据算法1生成了15 000个故障场景,在这15 000个场景中经过切负荷量与断线数量初步筛选后依据K-means聚类分析原理将筛选出的场景聚成k类,k的值由肘部法则确定。在不同的k值下,聚类结果的SSE变化情况如附录图A5所示,根据肘部法则认为k取4的聚类效果最佳。
(2)不同线路加固方案下DG规划结果。
为得到在每种线路加固方案下相应的电源配置情况,对优化模型进行求解,计算时长为2 min。对上述4种方案分别求解,得到的优化结果如表4所示。

表4 IEEE 123节点算例在不同线路加固方案下的DG布点定容分布结果Table 4 The DG planning results of IEEE 123-node system under different line reinforcement schemes
对所得的优化结果从极限生存能力与总投资的角度进行进一步分析。由表4可知,每种方案的DG总容量相同,因此其布置DG的投资也相同。分别将上述方案的极限生存能力,即第二阶段的目标函数值与无DG安装时的数值对比,如图9所示,方案7对配电网极限生存能力提升的效果最佳。

图9 IEEE 123节点算例在不同方案下的极限生存能力Fig.9 The ultimate survivability of IEEE 123-node system under different schemes
综上,在相同的资金投入下,上述方案对配电网的极限生存能力均有提升。经对比分析,方案7下的配电网极限生存能力提升效果最佳。因此选定方案3,即加固线路1-3、1-7、47-49、72-76、101-102,DG部署在节点48、49、65、101处,容量分别为800、165、800、598 kW。
5 结 论
本文提出了提升城市配电网极限生存能力的两步骤反脆弱规划方法,可提高台风灾害下城市配电网的防御力,保障重要负荷极限生存,从而提升电网韧性。在第二步DG布点定容规划中,为了保证所选出故障场景的代表性,在蒙特卡洛模拟过程中设置了很大的初始场景数量,并采取K-means方法筛选出代表性极端场景。此外,基于极端场景建立了均衡投资经济性和极限生存能力提升效果的两阶段规划模型。测试结果验证了规划方法的有效性。但本文仍存在不足之处,本文在建立规划模型时基于一些假设和简化,如假设台风灾害的概率及对配电网断线情况的影响是可以基于历史数据进行拟合建模得到。然而,实际情况中,极端事件台风的特征和影响可能存在不确定性和变化,这些假设的适用性需要进一步研究和验证。其次,本文所考虑的极端天气灾害类型单一。未来,将拓展研究范围,针对特大型城市电网,研究具有一定普适性的反脆弱规划方法,进一步提升城市电网韧性。
附录A

图A1 负荷变化曲线Fig.A1 Load variation curve

