巧用数形结合——数学教学不可或缺的“脚手架”

杨丽琼 周长军

（1.德宏州陇川县民族小学，云南 章凤 678799；2.德宏师范高等专科学校，云南 芒市 678400）

“脚手架”是盖任何高层建筑必需的施工辅助支架，这也是教师在课堂教学中引导学生在新旧知识点之间及学习过程中，联接不同思维认知阶段的辅助工具。“脚手架”搭建得恰当与否，直接影响到学生的认知程度与知识的有效习得。课堂“脚手架”确是个很贴切形象的比喻，设计搭建得好，是教与学过程中可视化的认知云梯。其中数形结合思想，对数学学习过程中存在诸如语言、思维方式、理解、表达、转换等障碍有一定困难的民族小学生而言，对于帮助其理解问题、发展抽象思维是不可或缺的“脚手架”，其意义和作用尤其是显得必不可或缺少和至关重要。

那么，在民族学生数学学习的教学实践中学习中，如何进行数形结合思想的渗透呢？

一、数形结合思想在数的认识中的运用

所谓数形结合思想，是一种包含“以形助数”和“以数辅形”两个方面的重要的思想方法。我国著名数学家华罗庚曾经说过:“数缺形时少直观,形少数时难入微”，道出了数形结合的辩证关系。

简而言之，数形结合就是把数学中“数”和“形”结合起来解决数学问题的一种数学思想，通过“数”与“形”之间的对应和转换来解决数学问题，“数”与“形”互相转化的过程，将抽象的知识具体化、形象化，再根据对图形的观察分析联想，从而掌握基本知识，增强对知识的理解能力，学生学起来就轻松多了。

例如:人民教育出版社三年级上册，学习的《分数的初步认识》，三年级下册《小数的初步认识》两种数，就是建立在数形结合的方法之上的。在《分数的初步认识》的教学中，教师指导学生对学具的操作，通过折纸让学生对分数的含义有一个直观的认识，先从1/2，让学生动手操作，通过折一折，涂一涂，画一画充分感知1/2，再判断能不能用1/2 来表示，在学生充分建立1/2 的表象基础上再来估一估1/3，充分利用多媒体课件的演示来加强直观教学，让学生加深对分数概念含义的理解，降低了对分数概念理解上的难度。（图1）

图1

《小数的初步认识》这部分内容是借助“元”“米”为单位的小数作为平台，让学生在具体的情境中初步认识小数，教师可借助几何直观，渗透数形结合的思想，帮助学生理解小数的含义。首先呈现把 1 米平均分成10 份的线段图，为学生用分数表示米和分米的关系提供直观支撑。其中箭头表示“从起点到这个位置的长度”为“1 分米”或“3 分米”。其次揭示一位小数的含义，并给出写法。最后让学生尝试写出“1.3”这个小数。（图2）

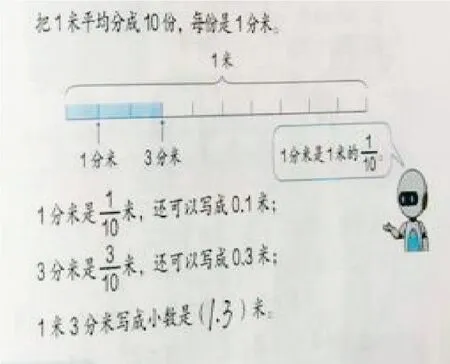
图2

分数、小数的初步认识是数的概念扩展，对于学生来说是比较抽象的，理解分数和小数的意义有一定的困难，课堂教学中，数形结合可以更好的帮助学生掌握理解这两种数的概念。

二、数形结合思想的在计算教学中的运用

在数学课程中，“数”与“形”互相联系，密不可分。通过数与形的结合，可以帮助学生直观地理解抽象的知识内容。

例如:在“除数是一位数的除法”笔算环节，依据学生的认知规律设计教学过程，让学生充分理解算理。通过给学生提供作为教具的小棒，让每个学生经历将42 根小棒平均分成两堆的过程之后，在汇报时教师应使用投影和板书，将分小棒的过程与书写笔算竖式的过程结合起来，在表达时重点突出计数单位，以便使学生明确每一次计算结果的含义。

当学生说“先将4 捆平均分成2 堆，每堆2捆”时，结合分的过程，教师先说明是“把4 个十平均分成2 份”，然后在竖式的十位商2，并说明这个“2”的含义是“每份先分得2 个十”；再在被除数下面写4，说明这个“4”表明“分掉了4 个十”；将2 写在横线下面，说明“还剩2 个一”。当学生说“再将2 根平均分成2 堆，每堆1 根”时，教师在竖式的个位商1，表明“每份又分得了1 个一”等。 （图2）

最后，得到完整的竖式，要告诉学生这是竖式的简便写法，中间过程中的一些0 可省略不写。之后安排“当十位上的数除后还有余数，应该怎么办？”这样不同层次的例题，引导学生获得对问题的认识、理解和解决的同时，也获得对数形结合思想的认识和感悟，只有经历数学知识的应用过程，才能体会数形结合思想的作用，才能进行知识的有效迁移。（图3）

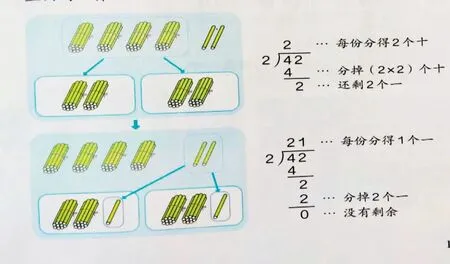
图3

三、数形结合思想的在图形的周长、面积中的运用

数学为人们提供了一种认识和探究现实世界的观察方式，通过数学的眼光可以从现实世界的客观现象中发现数量关系与空间形式，提出并解决有意义的数学问题。数形结合实际上是一个数与形互相转化的过程，既把题目抽象的问题形象化，再根据对图形的观察、分析和联想，逐步转化成算式，发现规律，应用规律，使问题得到解决。

例如:在计算图形的周长和面积时用数形结合的方法，更加直观，例如解决在方格纸上画几个长方形或正方形，使它们的周长（面积）都相等，然后比较一下它们的面积（周长），你有什么发现？ （图4）

图4

这个问题，目的在于引导学生进一步巩固周长与面积的概念，让学生用彩色笔描出图形的周长，再算周长和面积，结合具体的数据，组织学生结合相应的数据和图形的形状观察:什么变了？什么没变？体会面积相同的图形，周长不一定相同，周长相同的图形，面积不一定相同，而且正方形的面积大。数形结合就是通过数与形之间的对应和转化来解决数学问题，它包含以形助数和以数解形两个方面，利用它可以使复杂的问题简单化，抽象问题具体化，它具有数的严谨与形的直观之长，是优化解题过程的重要途径之一，是一种基本的数学方法。

四、结语

数形结合数学教学中,对于面临语言、理解、转换障碍的民族学生（事实上，不仅仅是面临上述障碍的少数民族学生），通过“看得见”的具体的“形”，可从直观上帮助民族学生对抽象的“数”及其运算的认知，加深理解；反过来，民族学生通过从具体的形象的“形”理解了“数”概念的内涵。

数形结合思想的教学，从民族小学生面临的“我知道它的意思，就是不会说”和教师常遇到“学生是懂的、但要么是怕说错、不敢说，要么表达出来不准确、不全甚至不对”，到学生轻松地说“我会用数学话说了”和教师“有针对性地进行语言表达纠偏、学生表达能力增强了”，民族小学生见到数量就应想到它的几何意义,见到图形就应想到它的数量关系；学会了数学地表达和转换，表明教学中恰当地运用数形结合这个“脚手架”，能够优化教学,成就别样的课堂，促进每个民族小学生的发展，提高课堂教学效率，具有进一步的现实作用和意义。