六自由度垃圾分拣机器人正逆运动学分析及构建工作空间的研究*

毛怡琳,李 悦,魏铭辰

(长春师范大学 工程学院,吉林 长春 130032)

0 引言

工业机器人是集机械、电子、控制、计算机、传感器、人工智能等多学科先进技术于一体的现代制造业重要的自动化装备,已成为国内外备受重视的高新技术产业[1]。运动系统是机器人系统的基础部分,它对机械设备的性能有着重要的影响。为探求垃圾分拣机器人在智能工厂上的摆放和控制问题,必须对其进行运动学分析和计算,本文主要针对垃圾分拣机器人的运动学进行分析。

1 机器人运动学分析

机器人运动学主要研究机器人关节变量空间和机器人末端执行器位置和姿态之间的关系[2]。六自由工业机器人中六自由度指存在六个运动副,在研究机器人运动时每个运动副之间假设用刚体连接(没有其他变形),姿态的改变仅与运动副上的自由度相关。常见的机器人运动学包括正向运动学和逆向运动学,正向运动学即给定机器人各关节变量,计算机器人末端的位置姿态;逆向运动学即已知机器人末端的位置姿态,计算机器人对应位置的全部关节变量。

1.1 基于改进型D-H法则建立连杆坐标系及连杆参数

空间中任意放置的两连杆有且仅有一条公垂线,故两运动副之间的距离为唯一解且关于公垂线的角度差也唯一,此时距离记为ai,角度记为αi,当空间上存在多个杆件连接,需要另外两个参数di和θi来描述相邻两线段ai-1和ai间的相对几何关系,其中ai-1和ai两垂线间的距离为di,角度差为θi,如图1为D-H参数空间表达改进型D-H参数,X轴的方向以当前的Z轴和最后一个关节的Z轴(即Zi+1轴)的叉乘方向使用右手定则:由Z轴转向Zi+1轴,大拇指方向为X轴方向,建模步骤为:

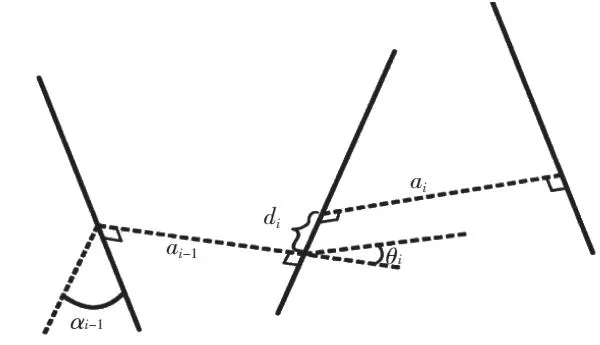
图1 D-H参数空间表达

(1)绕Xi轴旋转αi,Zi和Zi+1共线;

(2)绕Xi轴旋转ai,Zi和Zi+1重合;

(3)绕Zi轴旋转θi,Xi+1和Xi共线;

(4)绕Zi轴旋转di,Xi+1和Xi重合。

通过改进型D-H坐标系,可以确定机器人在零点方位的连杆坐标系,如图2所示。表1提供了机器人机构的改进型D-H参数,更好地满足实际应用需求。

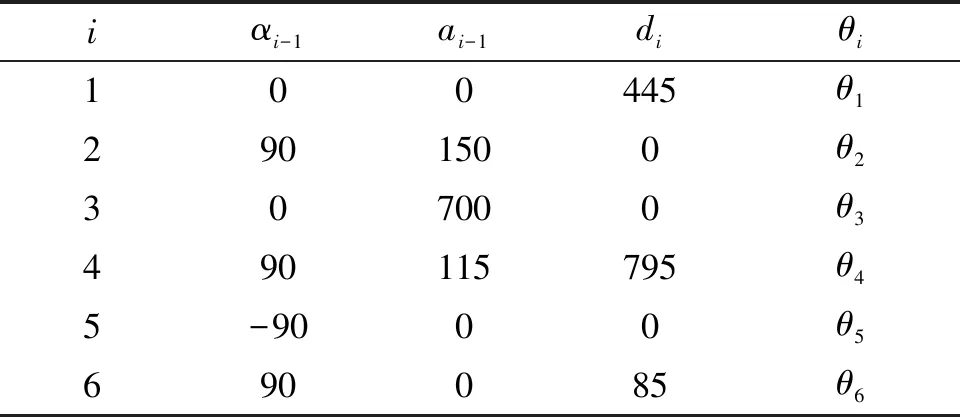
表1 改进型D-H参数表

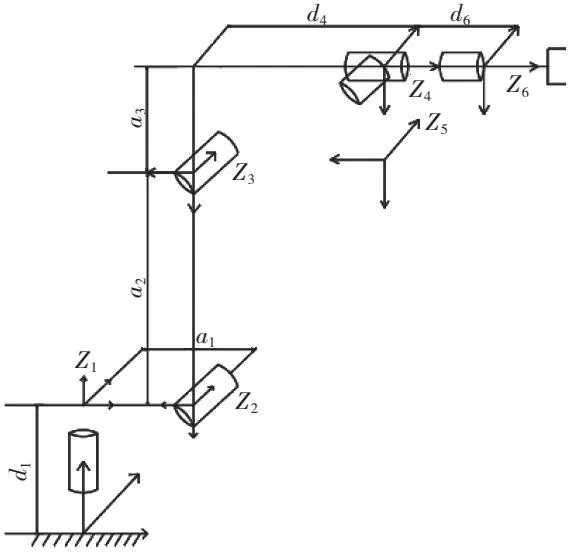
图2 六自由度工业机器人的连杆坐标系

1.2 正运动学分析

六自由度工业机器人正解是已知各关节的运动参数,求末端执行器的相对参考坐标系的位姿。

对于改进型D-H参数乘积顺序为:

Rot(zi,θi)×Rot(zi,di)

通过齐次变换矩阵

为了简化运算使用matlab进行计算,关键代码如下:

d1=795;

d4=795;

d6=85;

a1=150;

a2=700;

a3=115;

⋮

T1 = A1*A2*A3*A4*A5*A6;

将改进型D-H参数表带入齐次变换矩阵,得出六个矩阵,为简化计算此处使用MATLAB进行矩阵计算,运算结果中的px、py、pz即为机器人末位位姿x、y、z。

1.3 逆运动学分析

逆运动学分析通过给出的末端执行器的相对参考坐标系的位姿,求解机器人各关节运动参数。

在机器人运动学公式中,末端连杆位姿已经给定,即n、o、a、p已知求解关节变量θ1、θ2...θ6。

其中

(3)θ2=arctan2[-(a3+a2c3)pz+(c1px+s1py)(a2s3-d4),(-d4+a2s3)px+(c1px+s1py)(-a2c3-a4)]-θ3

此时θ1和θ3有四种组合,因此该θ2有四组解。

(4)当s5≠0:

θ4=arctan2(-a4s1+ayc1,-c1c23ax-s1c23ay+s23ax)

当s5=0时,六自由度工业机器人处于奇异状态,4与6关节轴重合在同一直线,此时θ4可以取任意值。

(5)θ5=arctan2(s5,c5)或θ5=θ5+180°

(6)θ6=arctan2(s6,c6)或θ6=-θ6

六自由度工业机器人可能存在8个反解。但是,由于结构的限制有些解不能实现,在机器人存在多种解的情况下,选出满足机器人工作要求的解。

2 运动学仿真

六自由度工业机器人运动学分析的正逆解算是在矩阵运算的基础上进行数据处理计算,而Matlab(matrix&laboratory矩阵工厂)中的Robotics Toolbox工具箱作为Matlab自带的工具箱可以实现包含齐次变换求解、正逆运动学求解、雅可比矩阵、动力学仿真及轨迹规划、机械臂的仿真等操作,对于垃圾分拣机器人机械臂通过表1 改进型D-H参数表,利用Matlab Robotics Toolbox建立机器人模型,关键代码如下:

% theta d a alpha

L1=Link([0 d1 a1 alpha1]);

L2=Link([0 d2 a2 alpha2]);

L2.offset=pi/2;

L3=Link([0 d3 a3 alpha3]);

L4=Link([0 d4 a4 alpha4]);

L5=Link([0 d5 a5 alpha5]);

L6=Link([0 d6 a6 alpha6]);

L1.qlim=[(-170/180)*pi,(170/180)*pi];

⋮

L6.qlim=[(-360/180)*pi,(360/180)*pi];

robot=SerialLink([L1L2L3L4L5L6],'name','maoyilin');

robot.plot([0,0,0,0,0,0]);

robot.display();

robot.teach;

hold on;

代码编写使用Link函数设置机器人连杆,qlim函数限制关节变量极限[min max],SerialLink函数连接连杆构成机械臂。

在上述代码中,robot.plot([0,0,0,0,0,0])用于输出机器人模型,后面的六个角为输出时的theta姿态;robot.display()打印出机器人改进型D-H参数表;robot.teach则是展示机器人模型;L2.offset = pi/2 表示连杆2相对于连杆1有90度的关节偏移量,因为连杆2的偏移量可以帮助机器人实现更多的运动空间,该偏移量通常被设置为90度。

上述由matlab建立的六自由度工业机器人模型如图3所示。

图3 Matlab Robotics Toolbox建立的六自由度工业机器人可视化界面

2.1 正逆运动学仿真验证

正运动学验证过程中,选取六个关节转角分别为(pi/3 pi/4 pi/5 pi/3 pi/4 pi/5)进行计算,通过计算取得正运动学位姿结果,如图4所示,逆运动学验证过程中选取位姿为(-132,-333,1807)进行计算,逆运动学带入公式计算转角,并将结果用Matlab仿真出来,和正运动学位姿对比。图6为正逆运动学位姿仿真对比。

将正运动学位姿计算结果(图4)与Matlab Robotics Toolbox建立的机器人仿真位姿结果(图5)进行数据对比,通过对比发现位姿计算结果误差在0.5以内,机器人建模与正运动学分析互相验证,结果正确。将逆运动学位姿带入公式计算,计算得出的角度代入建立的机器人仿真中,对正逆运动学位姿仿真对比(图6),经过对比显示与仿真位姿误差极小,逆运动学结果正确。

图4 正运动学位姿结果图5 Matlab仿真结果

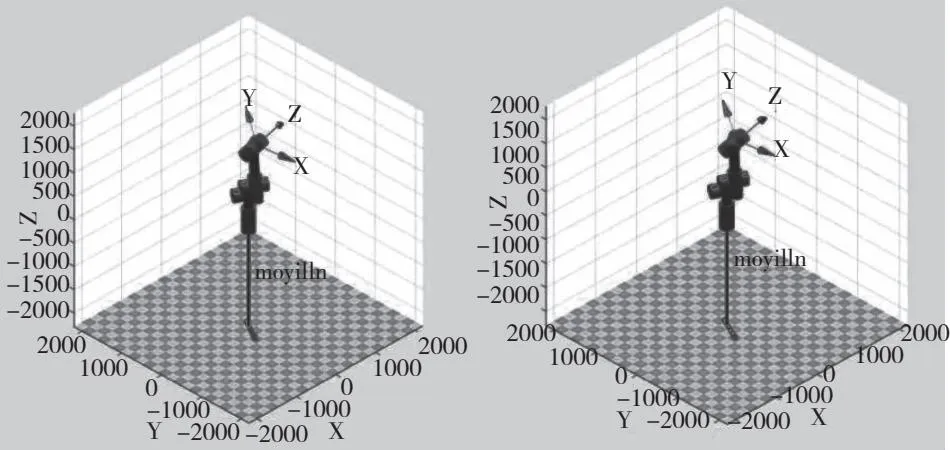
图6 正逆运动学位姿仿真对比

2.2 机器人工作空间的构建

工作空间是衡量机器人工作能力的一个重要的运动学指标[3],蒙特卡洛法是一种随机模拟方法,用于在计算机上估计某些统计量,对于要估计的统计量,通过模拟大量的随机抽样,并计算这些样本的随机值来估算这个统计量的值。蒙特卡洛法的优点在于,在处理许多复杂的问题时可以通过模拟来估计答案,而无需解决复杂的数学方程。

蒙特卡洛法求解机器人工作空间流程如下:

(1)建立机器人模型,设置关节旋转角度限制;

(2)设置随机工作点数目;

(3)在关节旋转角度限制下随机取得各关节角度得到随机点;

(4)所有末端点的随机点的集合构成机械臂的工作空间。

关键代码如下:

N=2000;

theta1=(l1d+(l1u-l1d)*rand(N,1))*pi/180;

⋮

theta6=(l6d+(l6u-l6d)*rand(N,1))*pi/180;

for n=1:1:N

q=[theta1(n),theta2(n),theta3(n),theta4(n),theta5(n),theta6(n)];

robot.plot(q);

p=robot.fkine(q);

a=zeros(3,1);

a(:,1)=p(1,1,1).t;

plot3(a(1,1),a(2,1),a(3,1),'b.','MarkerSize',0.5);

图7展示了基于蒙特卡洛法的机器人在工作空间中的运行情况。上述代码中,N=2000;为设置的随机工作点的数目,该数目可以根据需要进行适当加减;heta1=(l1d+(l1u-l1d)*rand(N,1))*pi/180;意为可以随机取得关节1的角度;通过MATLAB仿真的工作空间可以进一步确定智能工厂产线的机器人摆放问题。

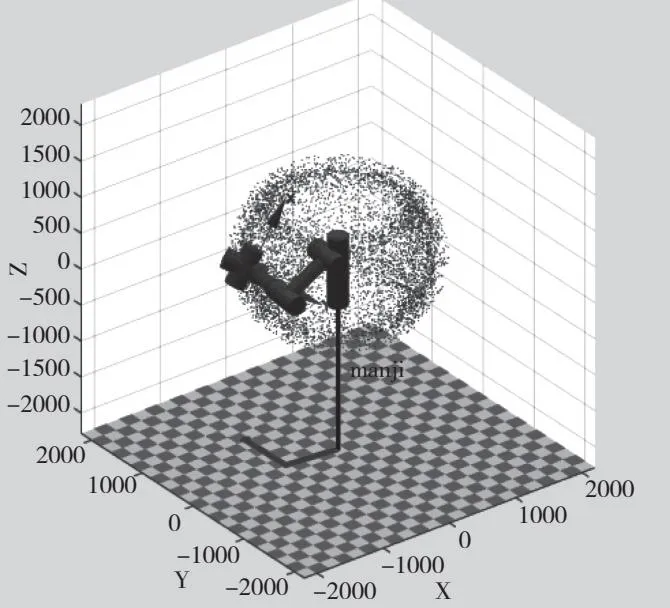
图7 基于蒙特卡洛法的机器人工作空间

3 结束语

本研究基于改进型Denavit-Hartenberg参数法,建立了六自由垃圾分拣机器人的正逆运动模型,阐述了正逆运动学分析与结算的具体过程,并在matlab环境下对机器人正逆解进行仿真验证,仿真结果显示正逆解解算结论是正确的,进一步确定了流水线上垃圾位置与机械臂位姿与关节角度的一一对应的关系,在正运动学基础上使用蒙特卡洛法对机器人工作空间进行仿真,确定了垃圾分拣机器人在智能工厂产线的摆放问题。