基于FTC-SA算法的孔群在机测量路径优化*

周 续,安 迪,王骏豪,张从鹏

(北方工业大学机械与材料工程学院,北京 100144)

0 引言

随着精密制造技术的不断发展,在机测量越来越广泛地应用于机械零件的加工精度检测中。相比于离线三坐标测量,在机测头测量具有成本低、无需二次装夹定位、便于后续工序加工等优势,同时可以将测量数据直接反馈给加工系统,实现加工误差补偿[1-2]。对于机械零件中的孔群特征,需要在孔群加工完成后进行孔心位置、孔直径、孔轴线的精度检测。而根据孔类型、孔尺寸、孔位置等信息编制的孔群在机测量程序,往往存在测头移位不合理、空行程距离过长等问题,导致生产效率低、机床能耗大[3]。

目前,孔群特征的加工/测量路径主要采用标准或改进的启发式算法进行优化,如遗传算法(GA)[4-5]、蚁群优化(ACO)算法[6-7]、模拟退火(SA)算法[8]、免疫算法(IA)[9]等。肖军民[4]根据孔的序号进行染色体编码,提出了一种基于改进遗传算法的孔群加工路径优化方法。龚玉玲等[5]则在遗传算法中引入模拟退火算法的Metropolis准则,以此来调节新种群的更新机制,提高了孔群加工路径在全局范围的寻优能力和收敛效率。ABBAS等[6]基于改进蚁群算法规划了矩形阵列孔群的加工路径。马旭东等[7]通过正交试验对蚁群算法的初始化参数进行优选,获得了全局优化的塑模孔群加工路径。张明禄等[8]先利用K-means聚类算法进行孔群分组,再利用改进模拟退火算法完成了孔群加工路径优化。戴红伟等[9]提出了一种自适应量子交叉免疫算法,在进行孔群加工路径优化时可以有效平衡全局搜索和局部挖掘能力。

上述研究主要针对孔群按类型或尺寸进行分组的加工路径优化情况,是快速有效的求解算法。然而在孔群精度检测时,通常无需进行分组处理,参与路径优化的个体数量倍增,使得各算法出现收敛缓慢、解的质量低、稳定性差等问题。本文针对大规模孔群加工精度的在机测量需求,提出一种波动式温度控制的模拟退火(FTC-SA)算法,以优化出高效率、低能耗的孔群检测路径。

1 孔群在机测量路径模型

如图1所示,在测量坐标系Om-XmYmZm中,触发式测头从安全平面上的作业零点出发,依次运动至各加工孔的安全点,然后沿Zm轴进给至目标点进行孔中心位置、孔直径、孔轴线的精度测量,最后返回到作业零点。为了减少问题的复杂性,对孔群在机测量路径模型作如下假设:

(1)测头直径和长度可以满足所有加工孔的精度测量要求,即测量过程中无需更换测头。

(2)阶梯孔的加工精度在一次探测过程中全部完成,即阶梯孔的各目标点共用一个安全点。

(3)测头在孔群中进行移位及探测时,进给速度保持不变。

(4)测头在确定的探测参数下进行各加工孔精度测量。

由此,对于某一组给定的孔群,其在机测量路径的总距离仅会受到测头在各加工孔之间探测顺序的影响。此时孔群在机测量路径模型可以转化为典型的旅行商问题(TSP):即测头的作业零点和各加工孔的安全点共同按自然数进行编码,构成n个城市(城市编码最小值为1,最大值为n),测头则对应旅行商人;旅行商人从某个城市出发,寻找出一条遍历所有n个城市一次并最终回到出发城市的最短路径[10]。

将n个城市的遍历序列用向量C进行表示,C=(c1,c2,…,cn,cn+1),其中cn+1=c1,表示旅行商人由最后访问城市返回到出发城市。则城市ci与城市ci+1之间的路径距离可以表示为:

(1)

式中:(xi,yi)和(xi+1,yi+1)分别为城市ci和城市ci+1在测量坐标系中的Xm轴、Ym轴坐标值。

按序列C遍历n个城市的总路径距离为:

(2)

则孔群在机测量路径模型对应的目标函数为:

D(Cbest)=minD(C)

(3)

式中:Cbest为优化的城市遍历序列。

2 FTC-SA算法设计

SA算法的思想来源于金属热处理工艺中的退火原理,是一种求解组合优化问题的随机寻优算法[11]。该算法可以在搜索过程中概率性地跳出局部最优解并趋于全局最优解,其关键核心为Metropolis准则:

(4)

ΔD=D(Cnew)-D(Cold)

(5)

式中:P为新解的接受概率,T为当前温度,D(Cnew)为新解Cnew对应的总路径距离,D(Cold)为当前解Cold对应的总路径距离,ΔD为新解Cnew与当前解Cold对应的总路径距离的差。

2.1 初始温度的设定

标准SA算法通常将初始温度T0设定为一个充分大的值,以保证更强的全局搜索能力,但会导致搜索时间过长。本文借鉴混沌寻优方法进行初始温度的设定。通过在解空间内随机选取m个可行解,可以计算得到各可行解对应的总路径距离。根据Metropolis准则,退火的初始温度可表示为:

(6)

式中:D(Cmax)和D(Cmin)分别为解空间内随机选取的m个可行解对应的最大和最小总路径距离,P0为设定的接受概率。

2.2 多邻域贪心搜索机制

通过多邻域搜索可以产生优质新解。本文对当前解进行4种形式的扰动操作来产生新解,如图2所示。

(a) 个体插入操作 (b) 个体交叉操作

(1)个体插入操作:在当前解中随机指定两个序列位置,将位置1的元素插入到位置2的元素后面。

(2)个体交叉操作:在当前解中随机指定两个序列位置,将两个位置对应的元素进行交换。

(3)区域插入操作:在当前解中随机指定3个序列位置,将位置1至位置2的元素插入到位置3的元素后面。

(4)区域倒置操作:在当前解中随机指定两个序列位置,将位置1至位置2的元素进行倒置。

同时借鉴贪心策略,将4种扰动操作中总路径距离最小的新解保留下来。这样既保证了新解较大的搜索范围,又提升了算法的局部寻优效率。

2.3 波动式温度控制函数

标准SA算法中常用的降温方式为快速降温和指数降温[12],两者均为单调递减式温度控制策略。由式(3)可知,算法对劣解的接受概率与温度直接相关。当退火至低温时,对劣解的接受概率很小,算法跳出局部最优的能力也基本丧失。而通过引入升温回火操作,可以重新激活劣解的接受概率[12-14]。

在文献[12]的基础上,本文提出一种改进的波动式温度控制函数,使得温度在总体趋于下降时,可以实现多次降温退火与升温回火。波动式温度控制函数表示为:

(7)

式中:Tk为第k次迭代时的温度,k为外循环迭代次数,α为温度衰减参数,β为波谷控制参数,λ为波动间隔参数。

该函数是基于指数降温函数和三角余弦函数进行实现的,不仅具有幅值波动特性,还实现了波峰和波谷递减。与文献[12]相比,该函数引入了β参数来控制波谷递减,更易于判断退火是否完成;与文献[13]相比,该函数的相关参数含义清晰且更易于初始化。

图3为4种不同降温方式下的温度控制曲线。从图3可以发现,当采用快速降温方式时,迭代初期温度下降过快,导致算法无法充分地进行全局寻优而早熟收敛。当采用指数降温方式时,降温速率由快变慢,尽管算法搜索更加充分,但在中后期的执行效率太低。以上两种方式在趋于低温时,对劣解的接受概率非常小,算法困于局部最优后将难以跳出。多次回火方式是对指数降温方式的改进,在达到某个低温时,通过升温操作拉升算法的全局搜索能力;但该方式下的温度下降缓慢,算法执行效率较低。而采用波动温控方式时,温度快速下降,算法寻优较充分且执行效率较高;在趋于低温时增加升温回火操作,提高劣解的接受概率,使得算法能够跳出局部最优而寻到全局最优;由于是多次退火操作,需要对当前最优解进行记忆,避免在迭代过程中遗失。

图3 温度控制曲线对比

2.4 FTC-SA算法流程

图4为FTC-SA算法流程图,具体的算法步骤为:

图4 FTC-SA算法流程图

步骤1:根据式(6)设定初始温度T0,同时对终止温度Tend、内循环迭代次数L、温度衰减参数α、波谷控制参数β、波动间隔参数λ、记忆向量Cbest以及外循环迭代次数k进行初始化设定,并根据城市编码随机产生一个初始解C0,令Cold=C0,T=T0;

步骤2:重置内循环迭代次数,令j=1;

步骤3:根据多邻域搜索机制对当前解Cold进行扰动,利用贪心策略确定新解Cnew;

步骤4:计算并比较新解Cnew和当前解Cold对应的总路径距离,若ΔD≤0,接受Cnew作为新的当前解,即Cold=Cnew;否则,按概率P接受新解;

步骤5:当k=1时,直接将当前解记录在记忆向量Cbest中;当k>1时,若当前解为更优解,将其更新在记忆向量Cbest;

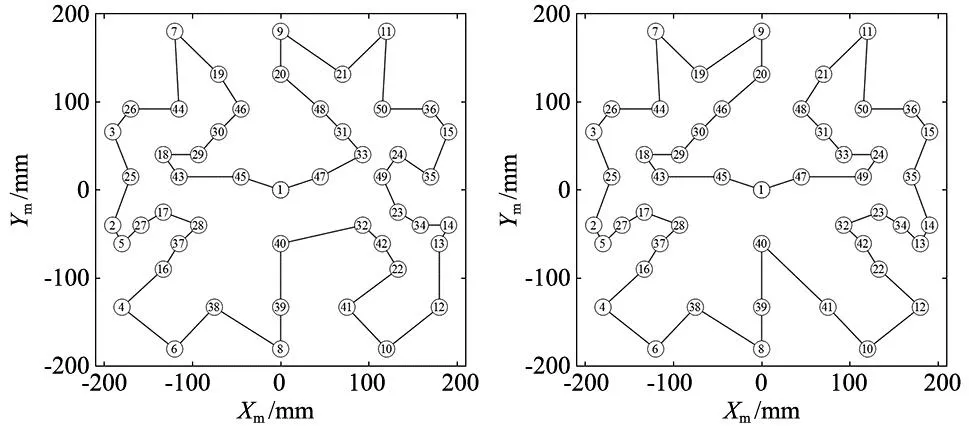
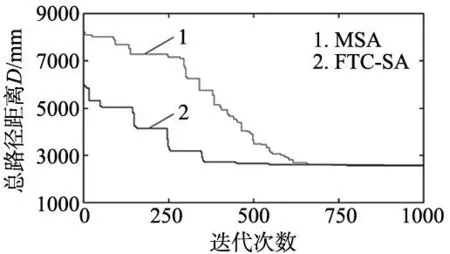
步骤6:判断是否完成迭代,若j

步骤7:判断是否完成退火,若T

3 试验结果与分析

图5 模具零件的孔群分布

利用MATLAB 2017b软件对本文所提的FTC-SA算法进行仿真,并与标准的GA、ACO、SA算法及多次回火升温的MSA算法[14]进行性能对比。FTC-SA算法的初始化参数设定如下:初始温度接受概率P0=0.6,终止温度Tend=0.001,内循环迭代次数L=200,温度衰减参数α=0.993、波谷控制参数β=1.2、波动间隔参数λ=100。

对各算法分别仿真10次,得到孔群在机测量路径优化结果,如表1所示。可以看出,FTC-SA算法优化的最优值和平均值均为最佳,其中最优值相比于GA、ACO、SA、MSA算法分别缩短55.52、42.12、9.7、4.85;平均值相应地分别缩短95.31、59.17、30.66、10.61。

表1 不同算法的优化结果 (mm)

将各算法优化的结果绘制成箱形图,如图6所示。箱形图是一种显示数据离散程度的统计图,可以体现出各算法优化效果的稳定性。可以发现,FTC-SA算法的箱形图位置最低,四分位距也最小,说明FTC-SA算法优化的解的整体质量和稳定程度为最好;MSA算法优化效果其次;GA、ACO、SA算法优化效果较差。

图6 不同算法的箱形图

MSA算法与FTC-SA算法优化的最短路径如图7所示,相应的迭代过程如图8所示。两种算法优化的最短路径均未出现交叉现象,但FTC-SA算法优化的解的质量更高。图7b对应的城市遍历序列为(1,45,43,18,29,30,46,20,9,19,7,44,26,3,25,2,5,27,17,28,37,16,4,6,38,8,39,40,41,10,12,22,42,32,23,34,13,14,35,15,36,50,11,21,48,31,33,24,49,47,1)。从迭代过程来看,FTC-SA算法表现出更强的解空间搜索能力,收敛速度也更快。

(a) MSA(D=2 583.37) (b) FTC-SA(D=2 578.52)图7 MSA与FTC-SA算法最短路径

图8 MSA与FTC-SA算法迭代过程

4 结论

合理安排孔群的在机测量路径,可以有效缩短测头空行程距离,提高检测效率,降低机床能耗。本文采用FTC-SA算法对大规模孔群的在机测量路径优化问题进行研究,建立了测头遍历路径的数学模型和目标函数;通过对标准SA算法中的初始温度设定、邻域搜索机制、温度控制函数进行改进,提高了算法的局部收敛性能和全局寻优能力;以某型号模具零件为对象进行了实例分析,结果表明本文所提的FTC-SA算法可以获得更好的求解质量和优化效果。