基于扰动观测器的挠性传动系统H∞解耦设计*
刘智康,孟范伟,庞爱平,刘云静
(1.东北大学秦皇岛分校控制工程学院,秦皇岛 066099;2.贵州大学电气工程学院,贵阳 550025)
0 引言
在工业应用中,挠性传动被广泛应用,但在是实际生产中有两个主要因素会恶化传动系统性能-连接执行器和负载的传动轴存在非线性环节(包括死区、饱和、间隙等非光滑的非线性特性),以及挠性系统的谐振模态往往具有弱阻尼特性[1]。两者轻则增加系统响应时间,重则产生较大的振荡和稳态误差,甚至导致系统不稳定。
近年来有很多尝试解决挠性系统弱阻尼特性的研究。WANG等[2]针对具有死区特性的挠性传动系统提出了一种非光滑多步超前预测控制策略,解决了死区特性的非光滑多值映射问题。LAGERBERG、DONG等[3-5]使用预测控制策略解决了带有间隙特性的机械传动系统控制问题。然而,WANG、LAGERBERG等[2-5]所研究的系统皆是输入动态线性子系统-非线性特性子系统-输出动态线性子系统,即线性子系统之间没有联系,对比输入子系统与输出子系统之间有反馈信号连接的系统更为简单。实际上后者线性子系统之间存在联系的系统更为现实对生活中普遍存在的挠性传动系统[6-11]的控制,那么在设计过程中既要考虑非线性环节对系统的影响,又要抑制谐振模态中弱阻尼特性引起的机械谐振以及机械谐振经过非线性环节后通过输出动态子系统反馈至输入动态子系统引起的振荡加剧的效果,同时也要留出一定控制裕度,所以控制器设计必须考虑综合控制要求。
H∞控制是一种综合的控制理论,可以综合考虑系统鲁棒稳定性、带宽、输出性能等多方面的设计要求[12-13]。但传统的H∞控制器阶次高、设计过程较复杂,另一方面控制器难以实现。本文优势在于预先设定控制器的结构与阶次,然后对具有固定结构的控制器通过H∞解耦进行参数优化求解,整体过程中增加了设计自由度。
针对挠性传动系统的已有研究多是基于单一结构,即连接非线性环节的前端和后端子系统无反馈信号连接。然而,本文研究的对象是两个子系统之间具有反馈信号连接的系统,弥补了现有研究的不足,而且针对挠性传动系统振荡加剧,提出了一种基于扰动观测器的PID-P复合控制策略,并给出了一种可以预先设定控制器结构与阶次的H∞解耦设计方法来进行控制器设计。
1 挠性传动系统模型与性能分析
典型的传动系统包括驱动电机和通过齿轮、轴连接的负载。齿隙的非线性会对传动系统的控制性能产生不利影响,不但影响控制精度还缩短了设备使用寿命,严重时会导致系统振荡、不稳定。带有齿轮结构的挠性传动系统如图1所示。

图1 挠性传动系统
图1中,Tm为电机转矩,ωm为电机转速,Jm为电机惯量,Kg为齿隙刚度,δ描述齿隙大小,Jg为负载惯量,Dg为齿轮阻尼系数,ωg为从动齿轮转速,Tg为齿轮力矩,Kc为传动轴刚度,Dc为传动轴阻尼系数,Tc为轴输出转矩,JL为负载惯量,ωL为负载转速,TL为负载转矩,σ为齿轮非线性环节的输出。系统的参数如表1所示。

表1 系统的参数取值
基于模型的补偿策略一直是在抑制或减弱齿隙非线性的问题中研究领域的热点。齿隙的死区模型是基于传动系统的传递力矩来表现齿隙效应,而传递力矩与系统的刚度和阻尼系数有关。死区模型的输入为主从子系统间的相对角度差,它们之间的传递转矩作为死区模型的输出。为符合齿隙效应的真实情况,死区模型考虑到了系统阻尼和刚度影响下的传动,齿轮的死区模型为:
(1)
式中:θm为电机输出的旋转角度,θg为反馈回来齿轮的角度Δθ=θm-θg为非线性环节的输入。
在图1中,从电机输出转矩Tm到齿轮转矩Tg的动力学方程为:
(2)
电机在转动过程中,电机转速ωm与齿轮转速ωg会因为传动装置产生变化,进而使电机转动角度θm与齿轮的转动角度θg存在角度差,得到的齿轮力矩为:
Tg=Dg(ωm-ωg)+Kg(θm-θg)
(3)
同理从齿轮力矩Tg到负载力矩Tc的数学模型为:
(4)
系统的数学模型式(1)~式(4)对应的结构框图如图2所示。
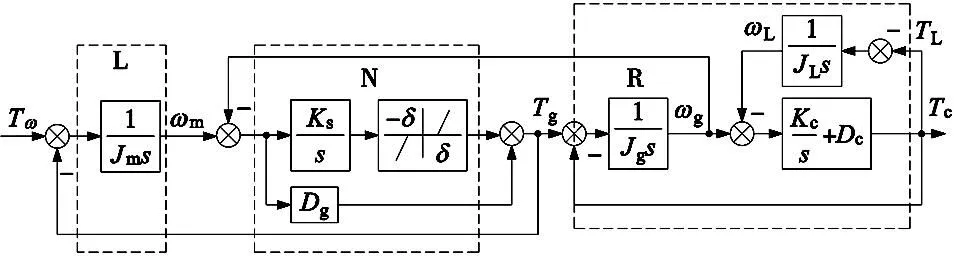
图2 挠性传动系统的结构图
图2中,N为非线性环节,L和R分别为前后端线性子系统。由图可知,子系统R的输入信号Tg影响了子系统L的输入信号。两个子系统L和R间有信号连接,并不是相对独立的两个子系统。这相对于目前已有的文献[2-5]控制研究中的线性-非线性-线性依次串连的挠性系统更具有真实性,设计难度更大。
图2中忽略间隙的影响,即δ=0时,从电机转矩Tm到轴转矩Tc的开环传递函数为:
(5)
式中:
a0=(Jm+Jg+JL)KcKg
a1=(Jm+Jg+JL)(DcKg+KcDg)
a2=JL(Jm+Jg)Kg+Jm(Jg+JL)Kc+(Jm+Jg+JL)DcDg
a3=JL(Jm+Jg)Dg+Jm(Jg+JL)Dc
a4=JmJgJL
将表1数据代入式(5):
(6)
系统的Nyquist如图3所示,可以看出开环系统穿越频率ωc=88.8 rad/s,相位裕度γ=8.85°。由此可得系统的稳定裕度太小导致系统稳定性极差。

图3 系统开环Nyquist图
稳定性极差原因分析:根据表1,阻尼系数Dc和Dg远小于刚度系数Kc和Kg,将其近似为0,式(5)可以简化为:
(7)
式中:
(8)
根据N(s)的表达式可以得到传动轴谐振频率ω1和齿轮谐振频率ω2,分别为:
(9)
被控对象Gp(s)的Bode图如图9中灰色的虚线所示。其频率特性在两个频率点出现谐峰,分别对应传动轴扭转振动和齿轮齿隙振动,这是Dc和Dg的值致使阻尼较小造成的,而且两种振动产生的间隔极小,从而导致系统谐振。齿隙的非线性影响在实际生产过程也是不能忽略的,从图2可以看出电机转矩信号Tm经过齿轮转矩Tg后,传递至后端传动轴,并反馈至前端与Tm作差,产生差值信号,而这个信号会再次经过死区,不断反馈使得系统谐振加剧,因此系统稳定性极差。
2 H∞解耦设计
传统的H∞控制设计是以矩阵的最大奇异值为衡量指标的一种综合优化设计,将具有多个性能要求的控制问题归结为含有一个H∞控制器和一个经过加权的综合性能输出(即系统广义对象)的标准H∞优化问题。其优点在于可以综合考虑多方面的性能要求,但传统的H∞设计只有一个综合的加权性能输出,多个性能指标互相牵制,且对单个性能要求没有针对性。另外,传统的H∞设计所得到的控制器往往阶次很高,不适合实际系统的应用。
本例中的挠性系统控制设计中涉及多个控制目标,因此本文提出H∞解耦设计方案。相对传统的设计方法,其优越性在于可以预先设定控制器的阶次,即可以给出一个相对低阶的控制器。既保留了传统设计的综合性,又可以针对每一个性能要求进行加权设计,构成一个含有多维性能输出的对角矩阵,进行性能综合优化。
该解耦控制系统设计一般可分为3个步骤:
步骤1:要根据控制目标和系统结构预设控制器的结构,这个控制器的结构可以是单一的低阶控制器或多控制模块的复合控制器结构;
步骤2:分析系统的性能要求,这里的性能要求应包含一般的设计中都应该具有的性能要求(例如带宽要求、鲁棒性要求、灵敏度要求等),还包含特殊系统的特定性能要求(例如跟踪性能、精度要求、输出限制等),根据控制对象的具体性能要求选择加权函数,构建含参数的加权的性能输出矩阵;
步骤3:采用解耦求解方法对上述构建的性能加权矩阵进行参数优化,得到满足多维性能要求的最优控制器参数。
在2.1节中具体的分析了本例中挠性传动系统的控制器结构,以及设计中涉及的控制目标和性能要求。在2.2节给出了针对每一个性能要求的加权函数的选择方案;2.3节是根据确定的加权性能,给出这个H∞解耦设计的最优控制器。
2.1 复合控制器的结构设计
在挠性传动系统设计中,忽略齿隙的影响,PID控制可以校正系统的弱阻尼模态获得较好的控制性能。若想获得易于实现的小增益控制器,可以在PID控制的基础上引入比例反馈或者前馈进行补偿,即PID-P复合控制策略。但实际上齿隙环节是不能忽略的。图4a与图4b分别为系统在PID-P控制策略下,阶跃信号大小为5 N·m时,控制器的输出信号与系统的阶跃响应曲线。由图4a可知,因为死区的存在,控制器信号持续震荡,从而导致图4系统输出同样持续振荡,PID-P难以获得好的控制效果。因此如果要保证系统稳定性,那么就要解决挠性传动系统中死区的影响。当然,还要综合考虑系统的性能需要,包括跟踪性能、扰动抑制和鲁棒稳定性等控制要求。
对于挠性传动系统,由于采用齿轮传递信号,齿轮力矩反馈至齿轮前端经死区非线性后引起振荡加剧,其中从动齿轮对驱动电机的反向力矩影响更直接。为此将系统结构中的反馈齿轮力矩当作扰动信号来处理。一般可将误差信号的积分控制作为一种扰动补偿方法,但该方式仅适用于恒值扰动。如果系统中的扰动频繁变化,就需要采取专门的补偿策略。
常用办法,可以设计一个扰动观测器,将得到的扰动估计值加到控制输出进而实现补偿[13]。传统的干扰观测与补偿方法是把干扰作为其它系统的输出,并估算该系统的状态,从而得到扰动信号的估计值用于补偿。而本文提出的反馈型扰动观测器补偿方案,是利用对象的输入输出数据对扰动进行估计和补偿,其原理如图5所示。
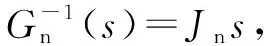

图6 挠性系统闭环控制
图6中虚线框内为待优化的可调复合控制器,由以下3个可调模块构成:
(1)Gc(s)为PID控制器,用来校正系统的弱阻尼挠性模态,保证系统的稳定性。
(2)前馈环节Kf用来改善低频段的幅频特性,减小系统的稳态误差。

接下来,需要解决的问题是如何将控制器参数的确定转化为H∞控制器的优化求解问题。
2.2 H∞加权函数选择
系统控制设计的性能要求主要有3个,即跟踪性能、系统带宽要求以及鲁棒性要求。下面将对以上的性能要求,分别选取适当的加权函数。
稳定裕度:根据图3,相位裕度γ=8.85°,系统稳定裕度过小,为了提高系统稳定性,控制器设计的第一个性能要求是鲁棒稳定性。鲁棒稳定性可通过限制灵敏度函数的最大值实现,也就是对系统的Nyquist曲线距离(-1,j0)的距离设定下限要求。其要求为:
(10)
式中:T1(s)为Tm到Tg的传递函数,γ为范数指标,W1(s)为权函数,为了限制灵敏度函数的增益上限,这里取W1(s)=1.44。
带宽要求:设T2(s)为T*到Tc的传递函数。系统带宽要求如下:
(11)
加权函数W2(s)的选择应满足扰动对传动轴转矩Tc的影响最小化并且保持在3.4 rad/s以下,它可以保证Tc有良好的信息传递。此外,应该减少系统未建模高频动态的影响,这些要求权重函数为:
(12)
跟踪要求:为了保证系统有更好的响应性能,参考模型Gref(s)定义为:
(13)
同时,为了保证系统输出信号可以跟踪参考模型Gref(s),T3(s)为参考输入T*到e的闭环传递函数。即要求:
(14)
要跟踪的参考模型的带宽应该低于系统带宽。增加精确跟踪要求低频段的跟踪误差应小于-6 dB,指定权重函数W3(s):
(15)
2.3 H∞解耦设计参数求解
具有n个性能要求的控制器参数的H∞解耦设计求解方法的框图如图7所示。

图7 多性能H∞解耦设计框图
图7中,w1,w2,…,wn为扰动输入,z1,z2,…,zn为经过加权的性能输出,将多个性能要求对角排列形成多重性能解耦的性能加权矩阵,图7中的P1(s),P2(s),…,Pn(s)是与控制对象和加权函数相关的传递函数矩阵,与虚线框内预先设定的反馈控制器R(a)构成了本文所提H∞解耦设计方法的标准框图。本文提出H∞解耦求解方法具体实现过程如图8所示。
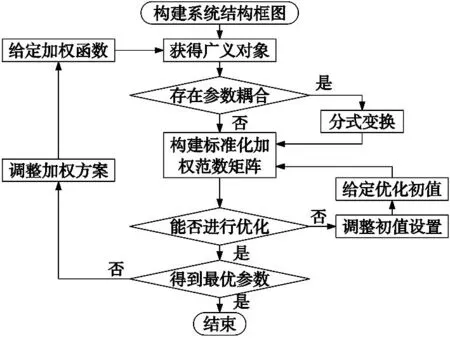
图8 H∞解耦设计参数求解流程
需要注意的是,H∞控制器R(a)中含有分子分母参数耦合的问题。可采用嵌套分式变换的方法,提取确定结构的控制器中的参数来进行H∞范数计算和参数化设计,即将预先设定的控制器参数提取,转化生成一个形如R(a)=Fl(M,a⊗I)的线性分式变换的形式,其中,M为与R(a)相关的一个固定矩阵,a为其中的可调参数。以本文具有式(10)、式(11)、式(14)3个性能要求的H∞设计为例,通过优化可调参数得到满足式(16)的最小值γ。
(16)
式中:H=diag(W1T1W2T2W3T3),此时所得到的可调参数即为系统控制器的最优参数。
在求取该H∞控制器中的最优参数时,将式(10)、式(11)、式(14)中的T1,T2,T3应用线性分式变换(LFT),提取含有参数的控制器C(即图6所示的复合控制器),表示成如下的线性分式形式P1,P2,P3来进行参数优化:
(17)
则可根据图8所示,可获得复合控制器的最优参数为:
(18)
此时的范数指标γ=1.15。
3 仿真分析
图9为系统控制前后的Bode图,图中的虚线和点划线分别为系统式(7)以及复合控制器式(18)的闭环Bode图。可以看出,基于扰动观测器的复合控制策略,使挠性传动系统获得较好的转矩传递性能。

图9 系统的Bode图 图10 控制器下的系统开环Nyquist图
图10为在H∞控制器作用下系统的开环Nyquist曲线。系统的稳定裕度由8.85°提高到了44.1°,能够满足系统的稳定性要求。
在H∞控制器作用下系统的频率特性和灵敏度特性曲线如图11所示。图11a中的实线为T*到Tc的传递函数T2的Bode图,而虚线为式(12)所示W2的倒数的Bode图。根据图中曲线的位置和变化趋势可知,T2总是小于1/W2,即解耦设计获得控制器能够使系统满足式(11)所示的带宽要求。灵敏度函数的峰值是系统的一个重要指标,图11b为在H∞控制器作用下系统的灵敏度曲线。由图可以看出,设计的控制器可保证谐振模态在稳定裕度范围内摄动时低频段是具有鲁棒稳定性的。
为了验证所设计的控制器的性能,在输入端T*输入一个正弦指令,结果如图12所示。图12a为在正弦信号下,参考模型Gref的参考输出和实际输出Tc的对比,从图中可见,系统可以跟踪参考输出。
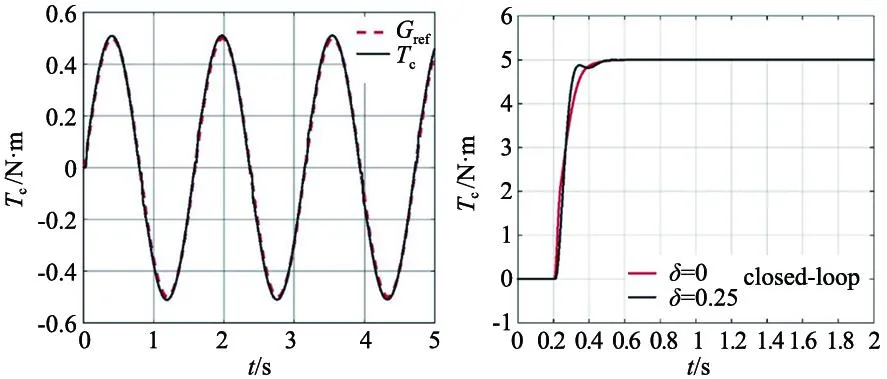
(a) 系统正弦响应 (b) 系统阶跃响应图12 系统的正弦响应和阶跃响应曲线
图12b为模拟输入T*为阶跃信号时系统的响应曲线,可以看出,提出的复合控制器可以较好地抑制挠性系统的振荡和齿隙影响。且当齿隙参数发生变化时,系统仍具有较好的响应特性,因此复合控制系统具有较强的鲁棒性与稳定性。
4 结论
针对挠性传动系统的弱阻尼挠性模态以及传动环节中齿隙非线性因素引起的振荡问题,给出了一个结构简单且具有较高鲁棒性的复合控制器。并采用H∞解耦设计,通过加权函数的选择限制系统的带宽和鲁棒性来确定控制器的未知参数。仿真分析表明,齿隙参数发生改变,闭环系统仍然具有较好的转矩传递性能。文中所采用的控制策略和控制器参数的H∞解耦求解方法不但可以综合考虑多方面的性能要求,而且可根据实际需求设计控制器的结构,更重要的是解决了传统H∞设计的控制器阶次高的问题,便于H∞控制器实际应用。

