考虑激光雷达误差的环境特征识别斜率差优化*

匡 兵,邱德宪,黄春德,黄廷辉,崔更申

(桂林电子科技大学 a.机电工程学院;b.计算机与信息安全学院,桂林 541004)

0 引言

近年来,随着自主移动机器人技术的发展,在工业、农业和服务业等各种不同领域的应用范围不断扩大。机器人自主移动需要导航系统,定位是实现导航的关键之一[1]。环境地图用于描述周围环境信息,是机器人定位的基础。移动机器人建立环境地图的重要前提是能对环境特征中的特征点或特征线段进行准确有效地提取[2]。在提取环境数据时通常使用激光雷达,激光雷达扫描速度快,测距精度高,角分辨率高,方向性强,广泛用于机器人定位。基于激光雷达的环境特征提取是当前移动机器人定位研究的热点之一。

基于激光雷达的室内环境特征提取的一个主要内容是线段提取。目前,线段提取技术主要可以分为序惯方法和递归方法两类。序惯方法有PDBS(point distance based methods)算法、SEF(successive edge following)算法和LT(line tracking)算法。递归方法有IEPF(iterative end point fit)算法[3]和Split-Merge算法[4]。除此以外,还有不依赖于局部信息的HT(hough transform)算法[5]。现有的多数序惯类算法都存在无法对相交直线进行分割的缺点。递归类算法存在对线段过分割或欠分割的现象。HT算法严重依赖于扫描点的空间密集程度。

满增光等[6]提出了一种分开-合并框架,该方法较好地解决了IEPF算法固定阈值所带来的过分割或欠分割的问题,降低了误分割率,取得了较好的特征提取效果,但是计算量依然偏大,计算效率较低[7-10]。综上所述,目前从激光雷达距离中提出直线特征的方法较多,但普遍采用迭代计算,依然缺少一种高效、简便、准确率高的算法。刘朋等[11]提出一种利用斜率差对线段进行分割和特征点提取的基于斜率差的激光雷达环境特征提取方法。该方法使用相邻点之间斜率的变化关系来提取特征点,再通过特征点对点云进行分割来提取线段,本算法不需要迭代,工作量较小,而且对阈值不敏感,准确率也较高。然而在基于斜率差的激光雷达环境特征提取方法中,尽管激光雷达测距精度较高,但是仍然会有误差存在,测距的误差在某些时候会造成角点和断点识别的错误,进而导致线段过分割现象和误分割现象。本文分析了导致该问题的原因,并提出了一种考虑激光雷达误差的环境特征识别斜率差优化方法。

1 基于斜率差的特征提取

图1 扫描点示意图

(1)

令第i点的斜率ki为:

(2)

因为由几何关系得:ω3=ω2+Δθ=ω1+2Δθ,所以:

k3-k2≈k2-k1≈0

(3)

当相邻两点处的k值之差很小时,就认为该两点处于同一条直线上,否则该点为断点或角点。令相邻激光点斜率的差值:

Δki=ki-ki-1

(4)

激光雷达扫描得到的点集为:

Q={(θi,di),i=2,3,…,n}

式中:θi和di分别为扫描第i点时转过的角度和到雷达的距离。寻找断点和角点并进行分割线段的算法为:

(1)计算相邻激光点斜率的差值Δk,即:

(5)

(2)如果相邻的3个激光点斜率的差值Δki-1、Δki和Δki+1均大于阈值kth且|Δki-Δki-1|>2kth,|Δki+1-Δki|>2kth,则认为第i点是第一类孤立点。找出所有第一类孤立点,删除后更新点集Q。

(3)更新点集Q后,再依次计算第i个扫描点的θi与相邻两扫描点的θi-1和θi+1的差值,如果|θi-θi-1|>θth,且|θi+1-θi|>θth(θth为阈值),则认为第i点为第二类孤立点。找出所有第二类孤立点,删除后再次更新点集Q。

(4)将去除孤立点后的点集Q重新利用式(5)计算相邻扫描点的斜率差值,进行断点和角点的判断。判断规则如下:

①如果|θi+1-θi|>θth,则第i点和第i+1点均为断点,分别为前一条直线上的结束点和后一条直线的起始点;

②如果Δki和Δki+1均大于阈值kth,且ΔkiΔki+1<0,则第i点和第i+1点均为断点,分别为前一条直线上的结束点和后一条直线的起始点;

③如果有|Δki|>αkth(0<α<1),而且还满足|Δki+1-Δki|>0&|Δki-Δki-1|>0&(Δki+1-Δki)(Δki-Δki-1)<0,则第i点为角点,即前一条直线的结束点,同时也是后一条直线的起始点,其中,α为角点阈值系数。

(5)根据点集Q中各点的属性,从第一点至最后一个点依次分割,并计算每条线段的始末点坐标和线段的斜率,得到线段集L。

在实际应用中,由于激光雷达数据存在误差,会导致两个问题,一是在角点处可能无法识别真实角点,二是在直线上可能会识别出错误的断点和角点。

2 角点处误差对特征提取造成的影响

因为雷达数据的误差会影响角点识别算法,导致真实角点无法被识别。通过一种角点识别优化算法,来提高真实角点识别准确度。

2.1 真实角点识别错误分析

从O点向直线L以等角度Δθ的间隔画直线,交点依次为Q1,Q2,Q3,Q4,Q5,O点到交点的长度依次为d1,d2,d3,d4,d5。雷达的距离数据存在误差,在获取OQ3时,雷达距离数据为OE1,雷达误差为E1Q3,此时d3的长度较长,ω2、ω3因雷达误差而减小,则|Δk3|也减小。因为该情况下ω2、ω3、|Δk3|的值变化非常小,所以雷达误差对识别角点E1的影响非常小,点集信息如图2a所示。

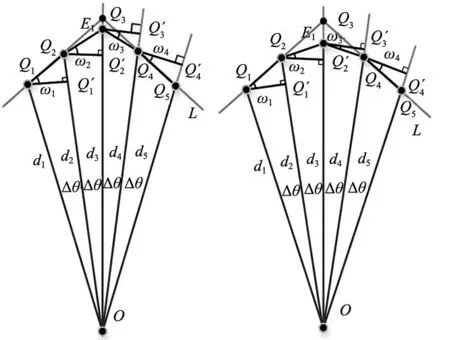
(a) 远距离角点 (b) 近距离角点图2 角点误差扫描点示意图

但是如果在获取OQ3时,d3长度比较短,雷达距离数据为OE1,雷达误差E1Q3长度不变,那么点集信息如图2b所示。可以看到虽然雷达误差距离没变,但是d3变小了,所以雷达误差对识别角点E1产生的影响也产生了变化。此时ω2、ω3、|Δk3|的值减小程度更大,若|Δk3|小于设置的角点判断阈值αkth,则角点E1识别失败,真实角点识别准确度降低。

2.2 真实角点识别优化

在雷达到角点距离相同的情况下,如果雷达到角点的射线与角点两侧直线的夹角发生变化,角点的斜率差值也会发生变化。当雷达到角点的射线与角点两侧直线的夹角相同时,雷达所处位置称为角点中心处,如图3a所示,已知角点两侧直线的夹角为A,则ω5+ω6=A,ω5=ω6,ω6+ω3+Δθ=90°,因为Δθ非常小,所以ω2+ω5=90°≈ω3+ω6,ω2≈ω3,从而可以得到ω2+ω3≈|180°-A|,故而有:

(a) 角点中心处 (b) 非角点中心处图3 角点扫描示意图

|Δk3|=|-tanω3-tanω2|≈
|-tan(90°-ω6)-tan(90°-ω5)|

(6)

当雷达到角点的射线与角点两侧直线的夹角不同时,如图3b所示。已知角点两侧直线的夹角仍为A,根据之前推理可知,ω2+ω3≈|180°-A|,与图3a相比,ω2增大,ω3减小,且ω2增大和ω3减小的程度相同。此时仍有:

|Δk3|=|-tanω3-tanω2|≈
|-tan(90°-ω6)-tan(90°-ω5)|

(7)

参考正切函数曲线,在0°～90°的区间中,因为函数的斜率为正,并且斜率的变化率也为正,ω2>ω3,所以tanω2增大的量大于tanω3减小的量,|Δk3|变大,雷达到角点的射线与角点两侧直线的夹角间差值的绝对值越大,该角点的斜率差的绝对值越大。由上述得出结论:角点两侧直线夹角的角度为A,雷达到角点的射线与角点两侧直线的夹角相同时角点的斜率差绝对值最小,此时角点相邻点的最小斜率差绝对值为:

(8)

所以设置的角点判断阈值αkth要大于环境中存在的角点两侧直线夹角角度最大的角点的Δkmin。

若雷达到角点的距离大于Damin时,角点处相邻点的斜率差绝对值被影响后仍然大于设置的角点判断阈值αkth,则Damin称为角点误差临界距离。根据之前的结论可知,雷达到角点的射线与角点两侧直线的夹角相等时角点相邻点的斜率差值最小,所以只要该情况下被雷达误差影响后的角点相邻点的斜率差绝对值仍大于角点判断阈值αkth,则该距离下识别角点不受雷达误差影响。如图4所示,角点两侧相邻点的雷达误差E1Q2和E3Q4与角点处雷达误差E2Q3为相反数,并且使得角点两侧直线夹角变大,并且他们的绝对值都等于雷达最大误差值,称该情况为角点极端误差情况,此时角点相邻点的斜率差值受影响最大。

图4 角点极端误差扫描点示意图

已知角点两侧直线夹角的角度为A,雷达最大误差值为X,雷达角度间隔为Δθ,角点判断阈值为αkth,且αkth>Δkmin,在角点极端误差情况下,并且雷达到角点的射线与角点两侧直线夹角相同,ω2≈ω3,若此时角点Q3相邻点的的斜率差|Δk3|仍大于αkth,则角点识别不受影响:

|Δk3|=|-tanω3-tanω2|≈2|tanω2|

(9)

(10)

(11)

在正常情况下,如图3a所示,ω1≈ω2,ω3≈ω4,而且Δk4≈Δk2≈0,|Δk3|>αkth,Δk2+Δk3+Δk4<0,因而有:

|Δk2+Δk3+Δk4|≈|Δk3|

(12)

在一般误差情况下,如图2b所示,当角点出现误差时,ω2和ω3减小,|Δk3|会产生变化,若变化后的|Δk3|<αkth,则真实角点识别失败。因为此时Δk2的减少值等于tanω2的减小值,Δk4的减小值等于tanω3的减小值,并且tanω2的减少值与tanω3的减小值之和为Δk3的增大值,Δk2<0,Δk3<0,Δk4<0,Δk2+Δk3+Δk4<0,所以Δk2+Δk3+Δk4的值保持不变,|Δk2+Δk3+Δk4|>αkth。

在极端误差情况下,如图4所示,因为Δk2的减少值大于tanω2的减小值,Δk4的减小值大于tanω3的减小值,但Δk3的增大值仍为tanω2的减少值与tanω3的减小值之和,Δk2<0,Δk3<0,Δk4<0,Δk2+Δk3+Δk4<0,所以Δk2+Δk3+Δk4减小,|Δk2+Δk3+Δk4|增大,|Δk2+Δk3+Δk4|>αkth。

在两种误差情况下,在角点处都有|Δk2+Δk3+Δk4|>αkth,因此得到一种识别角点的优化方法:如果ki-1ki<0,并且|Δki-1+Δki+Δki+1|>αkth,则第i点为角点。

3 直线处误差对特征提取造成的影响

因为雷达数据存在误差,角点和断点的识别算法会受到影响,导致在直线上识别出错误的角点和断点。通过算法的优化把这些错误的角点和断点过滤掉,保证直线的完整性和正确性。

3.1 直线处出现错误的角点和断点

从O点向直线L以等角度Δθ的间隔画直线,交点依次为Q1,Q2,Q3,Q4,Q5,O点到交点的长度依次为d1,d2,d3,d4,d5。因为雷达的距离数据存在误差,在获取OQ3时,雷达距离数据为OE1,雷达误差为E1Q3,此时d3的长度较长,点集信息如图5a所示,可以得到:

(a) 远距离直线扫描点 (b) 近距离直线扫描点图5 直线扫描点示意图

|tanω2-tanω1|≈|tanω3-tanω2|≈|tanω4-tanω3|≈0

(13)

虽然在OQ3上出现了雷达误差E1Q3,但它对点E1的识别造成的影响不大,点E1仍被识别为普通点。

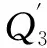
|tanω2-tanω1|≠|-tanω3-tanω2|

(14)

|tanω4-(-tanω3)|≠|-tanω3-tanω2|

(15)

且都不约等于0,Q2、E1、Q4的相邻点的斜率差值分别为:

Δk2=tanω2-tanω1>0

(16)

Δk3=-tanω3-tanω2<0

(17)

Δk4=tanω4-(-tanω3)>0

(18)

结合特征点判断规则,如果|Δk3|>αkth,则E1为角点,若此时|Δk3|和|Δk4|都大于kth,则E1、Q4为断点。

3.2 过滤错误的角点和断点

如图6所示,雷达距离数据OE1、OE2、OE3的雷达误差分别为E1Q2、E2Q3、E3Q4,若这些雷达误差的长度相等且为雷达的最大误差值,并且两边的雷达误差与中间雷达误差为相反数,并且中间点相邻点的斜率差绝对值最大,称该情况为直线极端误差情况。

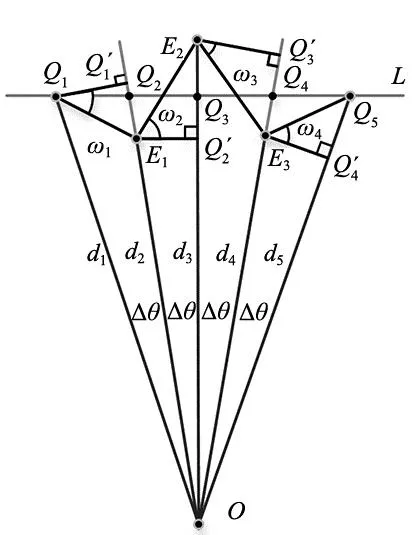
图6 垂直直线误差扫描点示意图

当激光射线与直线夹角越小的时候,雷达距离误差对普通点识别产生的影响越小,如图7所示,尽管在直线极端误差情况下,但仍有:

图7 小夹角直线扫描点示意图

|tanω2-tanω1|≈|tanω3-tanω2|≈|tanω4-tanω3|≈0

(19)

雷达误差E2Q3对普通点E2的识别造成的影响不大。

通过对比可知,当激光射线与直线垂直的时候,对特征点识别产生的影响最大,如图6所示。当雷达与墙面距离大于Dlmin时,若在激光射线垂直墙面且在直线极端误差情况下,仍未出现特征点的错误识别,则Dlmin称为直线误差临界距离。在该情况下,假设激光雷达最大误差为X,雷达角度间隔为Δθ且很小,E1Q2=E2Q3=E3Q4=X,OQ2≈OQ3≈OQ4≈d3,根据斜率差公式有:

(20)

(21)

(22)

角点判定条件为:Δk3>αkth(0<α<1)

断点判定条件:|Δk3|>kth,|Δk4|>kth

所以,

(23)

经过第二类孤立点的过滤后,在直线上出现的一对错误的断点之间的角度差非常小,它们之间的距离非常近,所以设置一个阈值Dline来过滤错误的断点,若两断点的直线距离小于Dline,则该两点视为普通点。

当提高了真实角点识别准确度并且对错误的断点进行过滤后,接下来设置一个阈值Dangle,来过滤掉直线上的错误的角点。如图8所示,Q1和Q9为断点,Q2～Q8为找出的所有错误的角点、错误的断点和真实角点,找出真实的角点Q6、Q3。

(a) 点簇(Q1～Q9)找到角点Q6 (b) 点簇(Q1～Q6)找到角点Q3

具体步骤如下:

步骤1:初始化,把断点内所有点组成点簇,设置一个对错误的角点进行过滤的阈值Dangle;

步骤2:通过点簇的起点和终点作直线;

步骤3:依次计算该点簇中其他点到直线的距离,找出到直线距离最大的点;

步骤4:如果该最大距离大于Dangle,则该点为真实角点,并在该点处把点簇分割为前后两个点簇,转步骤2;如果该距离小于Dangle,则在该点簇内无真实角点,结束判断;

步骤5:找出所有真实角点,结束。

4 实验及结果分析

测试环境符合真实的室内环境特征,而且测试环境中包含了该特征识别优化算法进行识别的所有特征情况,即两类断点和3种角度的角点(锐角、直角、钝角)。实际测试环境在某实验楼内搭建,如图9所示,设雷达坐标为原点,朝向角为Y轴正方向,该测试环境的几何坐标由皮尺测量而得。算法在STM32F103平台下进行,可视化结果图在MATLAB平台下得到,图中的点代表环境中的角点或断点,数字表示线段标号,如图10a所示。测试雷达选用某公司的RPLIDER S1型激光雷达,雷达固有误差为±5 cm,角度分辨率为0.391°,测试环境在激光雷达有效扫描范围内。实验中各参数如下:θth=2.3°,kth=0.97,α=0.9,Dline=20,根据式(11)和式(23)可以算出环境中雷达到每条直线和到每个角点的距离都未达到它们的Dlmin和Damin,所以该环境下有概率出现直线处识别出错误的断点、角点的情况和在角点处识别真实角点错误的情况。在实际测试中,放置雷达的时候,雷达实际朝向角与预设朝向角会有微小误差,所以最终得到的地图会有微小的旋转。

图9 实际测试环境

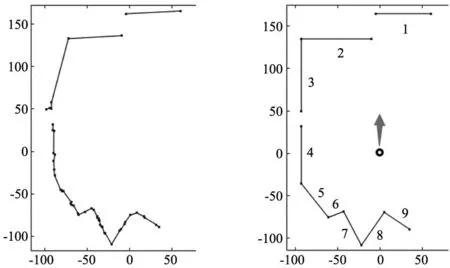
(a) 实际地图 (b) 原始斜率差特征识别算法效果

对算法进行优化后的效果如图10所示,在原始斜率差特征识别算法效果下,如图10b所示,通过与实际地图进行对比,可以看到在4～9号直线上识别出了多个错误的角点或断点,尽管在该情况下原本的一条完整线段被分成了多条线段,但是这些线段的斜率与原线段斜率相比变化不大,并且线段端点坐标仍在原线段周围。但是在2号3号线段连接处,角点识别错误,导致3号线段的斜率和线段端点坐标改变过大,并且两条线段的夹角变大。对角点识别算法进行优化后,效果如图10c所示,对比实际地图可以看出,地图中的所有真实角点都被算法所识别,与原始斜率差特征识别算法效果对比,在3号2号线段连接处,端点坐标和夹角发生了明显变化且更加接近实际地图。在过滤错误的角点和断点后,效果如图10d所示,解决了线段过分割问题,所有条线段都变完整。通过对整个优化过程进行分析,尽管4号5号线段、8号9号线段连接处,真实角点被识别后,与原始斜率差特征识别算法效果对比,线段端点坐标的变化不大,但是在过滤掉错误的角点和断点后得到完整线段的斜率产生了改变,且更加接近实际地图。

根据地图的匹配优化算法,可以进行相对定位,从而实现AGV小车的自主导航,自主导航结果如图11所示。

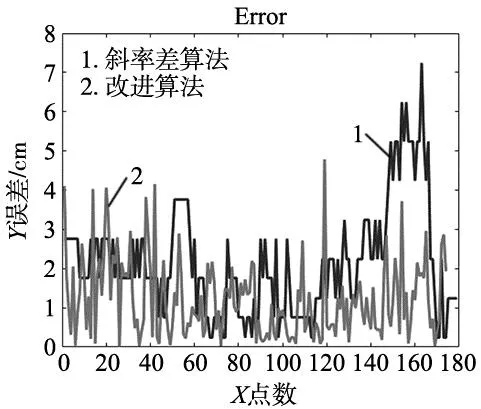
图11 自主导航路径误差结果图

在整个导航过程中,使用改进算法的AGV路径最大误差4.78 cm,平均误差1.21 cm,而斜率差算法的最大误差为7.24 cm,平均误差2.1 cm,改进算法的定位效果有了一定的提高。

5 结论

针对激光雷达距离数据的误差对基于斜率差的激光雷达环境特征识别算法的影响,本文分析了算法出现错误的原因,确定特征识别不准确的关键是角点和断点识别不准确,在误差情况下,利用真实角点与左右相邻点的相邻点斜率差值之和不变的关系优化角点处真实角点识别算法,提高了真实角点识别的准确度,利用阈值过滤直线上错误的断点和角点,提高了每条线段的完整性。实验结果证明该优化方法提高了基于斜率差的激光雷达环境特征识别方法的特征识别准确度。