基于OptumG2 的土体边坡稳定性破坏规律及影响参数分析数值模拟研究＊

王 敬，曾永庆

（1.长沙理工大学国际工学院，湖南 长沙 410114；2.湖南理工学院土木建筑工程学院，湖南 岳阳 414000）

岩土工程中，自然土质边坡稳定性问题是一个非常重要的基础性问题。在自然界中，边坡通常处于能够保持自身稳定的状态；随着边坡形状的变化以及施加在边坡上的外力的改变，边坡的内部抵抗力和外部扰动力也会发生动态变化。如果外力扰动过大，边坡就容易失稳，进而导致破坏[1]。

边坡的稳定性是工程建设管理中不容忽视的重要问题。边坡稳定性通常通过安全系数来评判。目前主要的分析方法有工程类比分析法、极限平衡分析法、数值分析法和非确定性分析法。相比传统的极限平衡理论分析方法，数值分析法可以避免花费大量时间搜索最危险滑动面，从而提高工程设计的效率[2]。在数值分析方法中，有限元强度折减法因其广泛适用性而受到了众多科研人员或设计人员的关注，但是在量化稳定性系数方面存在困难。而极限分析法需要预先设定最危险滑动面。有限元极限分析方法则能够兼顾这2 种方法的优点，无需预先设定最危险滑动面，同时还可以加快运算效率，适用于边坡、隧道等工程的初步设计计算。

目前，国内外学者关于边坡稳定性分析做了大量的研究，李双平[3]回顾了边坡稳定性研究的发展过程，详细阐述了主要分析方法的原理、条件，指出了可进一步研究应用的方法；张明等[4]将边坡稳定性分析的方法分为瑞典圆弧法、极限平衡法和数值分析法、可靠度法、模糊综合判断法、灰色系统法、人工智能法，详述了各分析方法的原理、优缺点以及适用性；蒋斌松等[5-6]对于边坡的平面和圆弧形滑裂面，采用解析方法建立了边坡安全系数的正确解析表达式，提出了通过求解一代数方程组来确定边坡的临界滑裂面和最小安全系数的方法；蒋中明等[7]针对土力学中渗透力概念模糊、计算方法不统一的问题，全面阐释了饱和土体中与水相关的作用力概念，基于有效应力思想的水土分算法将条块边界上所有的水压力都作为条块受力分析的荷载可以全面地反映渗透力的荷载效应，在考虑渗透力作用方面是精确的；潘永亮等[8]对花岗岩残积土边坡的降雨入渗规律进行深入研究，建立了一种适用于不同降雨工况的入渗模型，并采用数值模拟及前人经典模型计算结果对该模型进行了验证。随着西部山区铁路的建设，越来越多的铁路高边坡治理难题随之出现。燕彦君等[9]以某铁路高边坡工程为依托，结合现场工程实地监测数据，采用不同参数组合与数值模拟计算模型相结合的研究方法，进行铁路高边坡岩土体力学参数反演分析及后期铁路高边坡稳定性预测；为考察土体强度参数空间变异性对评价边坡稳定的影响，白桃等[10]使用概率方法评价对边坡稳定的适宜性，以简易Morgenstern-Price 法对土体参数空间变异性条件下的边坡稳定性进行了计算分析，单独使用安全系数或者失效概率都无法完整地对边坡稳定性作出评价，只有同时使用两者，边坡的安全评价才会更加安全有效。

边坡稳定性影响因素分析是工程实施中一项重要的内容，国内外有关边坡稳定性影响因素的研究很多，但不同边坡的因素却不尽相同。本文在此基础上，考虑了边坡土体的坡度、坡高、黏聚力、内摩擦角4 个因素对边坡稳定性的影响，借助OptumG2 数值模拟软件，运用正交试验设计，基于极限分析对9 个工况下均质土边坡建立模型与稳定性计算，获得各因素下安全系数随坡高、坡度、土体黏聚力、土体内摩擦角的变化关系。

1 OptumG2 数值模拟软件介绍

OptumG2 是一款集极限分析和有限元分析于一体的岩土分析软件，可进行三维有限元分析。OptumG2系列产品操作简单、建模迅速，支持CAD 文件导入，能自动加密网格；支持有限元极限分析，收敛性强；在复杂地质条件、复杂支挡结构的破坏模式分析、地基承载力分析、可靠度分析等方面具有优势[11]。

OptumG2 的算核建立在先进数值算法的基础上，目前仍然困扰普通有限元程序的如无法收敛及类似的数值问题，对于OptumG2 来说都不是问题，因而不需要进行烦琐和费时的算法参数的调整，所有精力可以集中于解决给定问题的物理本质。

OptumG2 针对所关注的物理量采用计算严格的上限和下限的方法代替了冗长的过程。利用得到的上下限解，可以立即估计精确解和误差范围，而这两者的精度都可以通过使用更多单元进行计算而加以改进。可以使用自适应网格加密进行分析，与解得的所关注对象的上下限相结合，自适应网格加密为得到精度高且计算成本小的结果提供了强有力的方法。

2 建模及数值模拟试验方案参数选取

结合某边坡实际工程，并考虑有限元建模的尺寸效应，确定边坡理论尺寸及土体参数特性如下：坡高分别为3 m、4.5 m、6 m，坡度分别为20°、40°、60°，土体黏聚力为10 kPa、20 kPa、30 kPa，土体内摩擦角分别为15°、20°、25°；土体重度为18 kN/m3。运用正交试验原理，边坡稳定性分析设计的数值模拟试验方案参数如表1 所示。

表1 土质边坡稳定性分析设计的数值模拟试验方案

本文采用摩尔-库仑本构方程进行边坡土体稳定性分析，该本构模型能够较好地描述岩土体的应力应变情况，并且所需参数易于获取；岩土层的物理实验和数值模拟试验的参考资料相对丰富，各种参数的取值范围有一定的经验依据，因此该本构模型具有广泛的应用价值[12]。

本次分析考虑了边界约束条件，根据选取的典型断面，左右方向为半无限土体空间，因此模型对土体的X方向位移进行约束；而模型底部认为既不能发生平移，也不能发生竖向移动，对模型底部的X和Y方向位移进行约束。对模型顶部不加约束，保持土体原本的自由状态。

基于有限元极限分析软件OptumG2，建立了土体边坡的有限元模型概念图及数值模型（如图1 所示）。在模型建立过程中，采用了强度折减极限分析方法，以求解边坡的安全系数。模型采用了长期时间条件，单元类型选为上限或下限，单元数量和初始单元数量分别为20 000 和2 500，并设置了自适应网格和4 次迭代。

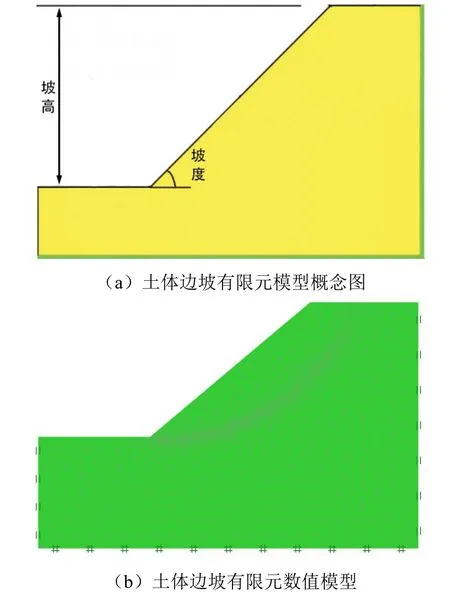
图1 土体边坡有限元模型概念图及数值模型

3 土体边坡稳定性破坏规律及影响参数分析

在数字模拟过程中，当塑性区贯通、滑动面应变或者位移发生骤变时，即可认为边坡发生破坏，此时的强度折减系数即为边坡安全系数。选取表1 中方案5作为典型边坡，该土质边坡滑坡过程如图2 所示。

图2 土质边坡滑坡过程

从图2 可以看出，土质边坡的失稳是一个由局部变形积累、局部失稳逐渐扩展到大变形、整体破坏的渐进过程。均质土体滑坡过程中，在重力作用下，滑动面上下的土体变形差迅速增大，产生滑动破坏，破裂面为圆弧滑动面，坡脚处的位移值最大。为判定边坡土体的坡度、坡高、黏聚力、内摩擦角4 个因素对边坡稳定性的影响，运用OptumG2 数值模拟软件对表2 中9 个工况进行稳定性计算，获得各因素下安全系数随坡高、坡度、土体黏聚力、土体内摩擦角的变化关系，具体结果如表2 所示，相应的正交试验直观分析如表3 所示。

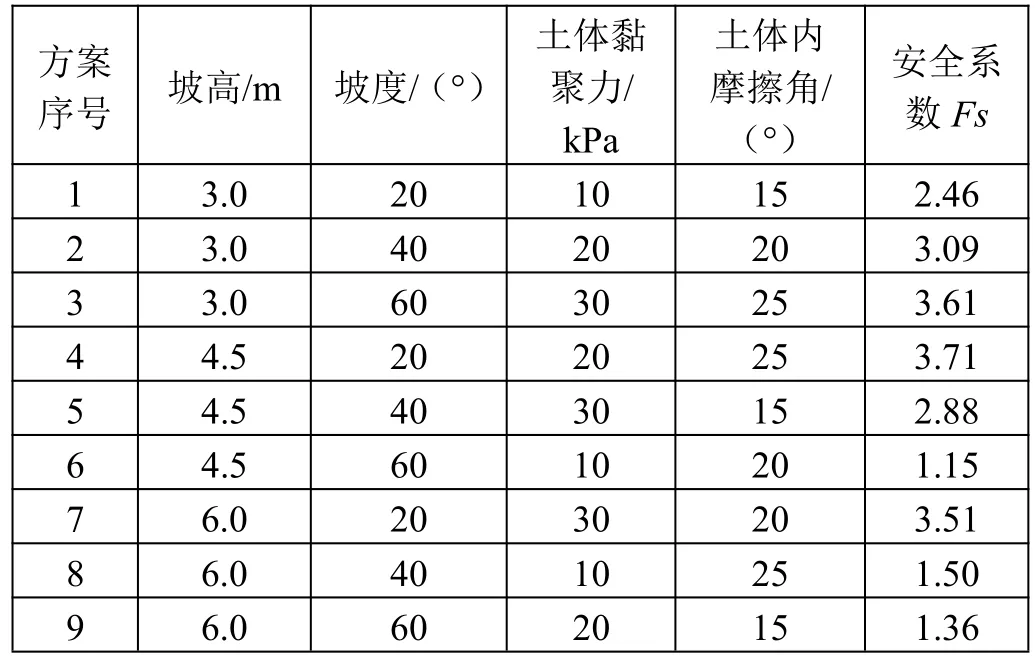
表2 土质边坡稳定性分析设计的数值模拟试验结果

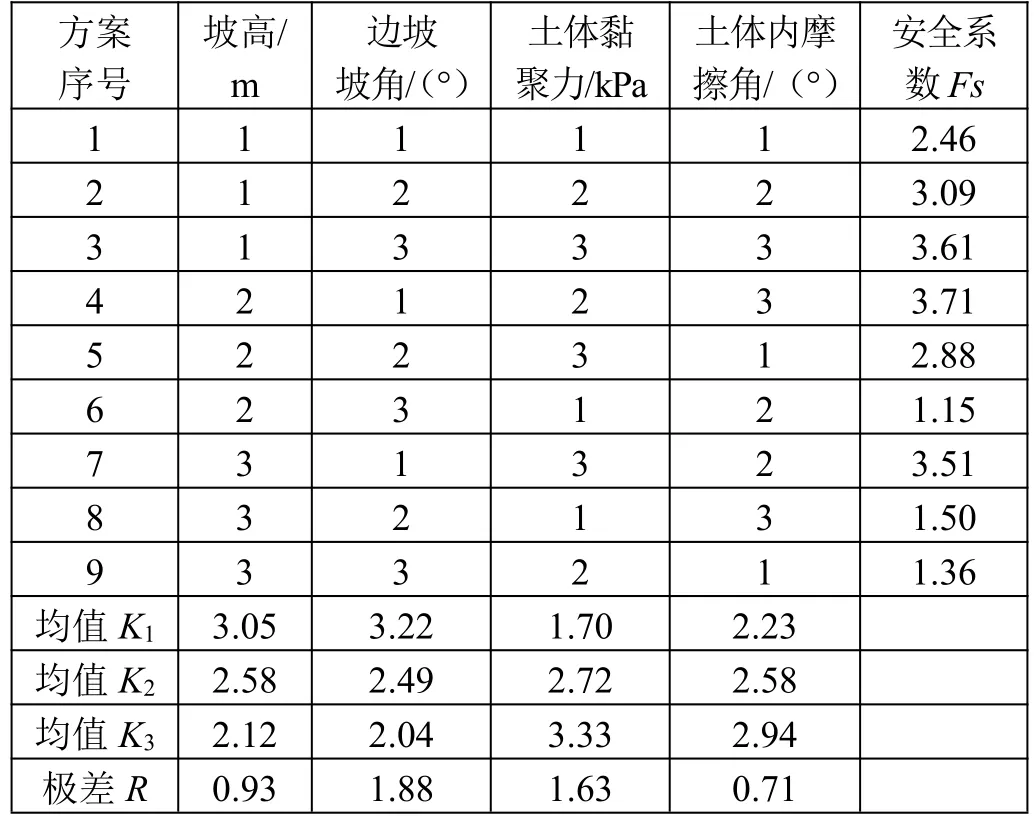
表3 土质边坡稳定性正交试验直观分析表

土体边坡安全系数随坡高、坡度、土体黏聚力、土体内摩擦角的变化关系曲线如图3 所示。随着坡高从3 m 增加到6 m，土体边坡安全系数近似直线地从3.05 下降到2.12；随着坡度从20°增加到60°，土体边坡安全系数近似直线地从3.22 下降到1.88。

图3 土体边坡安全系数随坡高、坡度、土体黏聚力、土体内摩擦角的变化关系曲线

随着土体黏聚力从10 kPa 增加到30 kPa，土体边坡安全系数近似直线地从1.70 上升到3.33；随着土体内摩擦角从15°增加到25°，土体边坡安全系数近似直线地从2.23 上升到2.94。极差R的大小反映了该因素变化时对实验指标影响的大小，根据极差大小的顺序对各因素的主次关系由大到小进行排列，可知对于土坡安全系数影响的大小排序依次为坡度、土体黏聚力、坡高、土体内摩擦角。

4 结论

本文借助OptumG2数值模拟软件分析了土质边坡的滑坡过程，针对边坡土体的坡度、坡高、黏聚力、内摩擦角素对边坡稳定性的影响，运用正交试验设计，基于极限分析对9 个工况下均质土边坡建立模型与稳定性计算，获得各因素下安全系数随坡高、坡度、土体黏聚力、土体内摩擦角的变化关系，主要结论如下。

土质边坡的失稳是一个由局部变形积累、局部失稳逐渐扩展到大变形、整体破坏的渐进过程，均质土体滑坡过程中，在重力作用下，滑动面上下的土体变形差迅速增大，产生滑动破坏，破裂面为圆弧滑动面，坡脚处的位移值最大。

增加坡高和坡度均会导致土坡安全性降低，引起滑坡破坏，增加土体的黏聚力和内摩擦角可有效增加土坡的安全性。