底部旋转型颗粒阻尼器减振性能分析

傅 博,陈 瑾

(长安大学 建筑工程学院,陕西 西安 710061)

0 引言

地震、风灾等自然灾害会引起工程结构剧烈振动甚至破坏,因此,近几十年来各国专家提出各种结构控制技术对结构振动进行控制[1]。结构控制中的被动控制[2]具有无需外部能源、造价低、构造简单等优点,因此受到广泛使用。颗粒阻尼器[3-4]是一种相对新颖的被动控制技术,最常见的形式是由容器盛有一个或多个颗粒,再将容器置于结构顶部,阻尼器随着结构一起振动,通过颗粒与容器壁碰撞、颗粒间碰撞和摩擦进行耗能减振。颗粒阻尼器具有造价低、作用频带宽、布置方便灵活、耐久性好等优点,在航空航天、机械等领域应用较为广泛,近些年在土木工程领域也逐渐引起越来越多的关注和应用[5-9]。

不难发现,颗粒阻尼器与调谐液体阻尼器(tuned liquid damper, TLD)有相似之处,TLD是通过晃动的液体和波浪对容器壁产生的动压力差以及液体运动引起的惯性力进行耗能减振,而颗粒阻尼器则主要是通过固体颗粒对容器壁的碰撞进行耗能减振。前期研究也证明了TLD与颗粒阻尼器在减振效果具有可比性[10-11]。为了提高TLD的减振效率,学者们提出了一些改进思路,其中一种思路[12-13]是在TLD容器底部安装旋转装置,通过旋转容器加速液体的晃动来增加耗能。鉴于TLD与颗粒阻尼器的相似性,本文将该思路引入到颗粒阻尼器中,提出一种底部旋转型颗粒阻尼器,将其与常规的底部固定型颗粒阻尼器对比,验证其在减振性能方面的优越性。

1 构造及工作原理

常规的颗粒阻尼器固定在结构顶部,本文称之为底部固定型颗粒阻尼器,其耗能主要靠颗粒与容器壁的碰撞、颗粒间的碰撞及颗粒与容器的摩擦,所以加速颗粒的运动可以有效增加阻尼器的耗能。基于该思路,本文提出一种底部旋转型颗粒阻尼器如图1所示,该新型阻尼器通过旋转机构将盛有颗粒的容器与主体结构相连。旋转机构由距离为ls的两侧弹簧(弹簧的刚度为kr)与中间的枢轴构成,颗粒阻尼器的容器可以绕枢轴中心旋转,容器底部到枢轴的中心的距离为l(转动杆的长度)。当图1中主体结构受到水平向地面加速度时,结构会产生响应(振动),从而带动底部旋转型颗粒阻尼器的运动,该运动可以分解成水平向运动和绕枢轴中心的转动。合理的设计旋转机构可以加速颗粒的水平向运动,从而增加颗粒与容器壁的碰撞,进而提高阻尼器的耗能和减振效率。类似的思路已成功用于提升TLD的减振性能[12-13]。

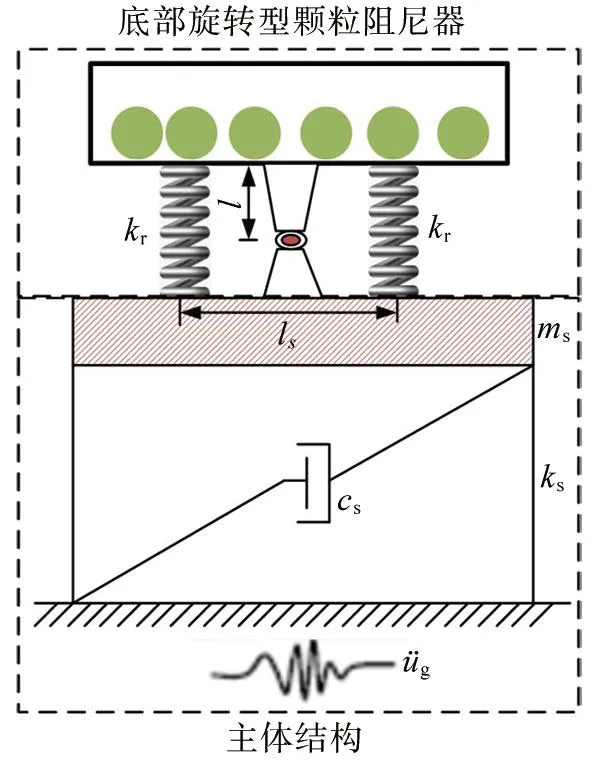
图1 结构-底部旋转型颗粒阻尼器体系示意图Fig. 1 Schematic diagram of structure-bottom rotated type particle damper system

2 计算模型及数值模拟

2.1 底部固定型颗粒阻尼器的计算模型

本文采用LU等[14]提出的颗粒阻尼器计算模型,该模型将常规多颗粒阻尼器等效为单自由度体系,被证明具有较高的计算效率和精度[4,14-15]。该模型源于PAPALOU和MASRI的研究[16],其核心思想是将多颗粒阻尼器等效为单颗粒阻尼器如图2所示,等效单颗粒质量等于多颗粒的总质量,假定阻尼力主要由颗粒与容器壁的碰撞贡献。

图2 等效单颗粒模型Fig. 2 Equivalent single particle damper model

图2中颗粒间隙d是确定阻尼力的一个重要参数,基于等效前后阻尼器腔体中的空隙体积相等的等效原则,其表达式为[4,14]:

(1)

等效颗粒阻尼器的刚度kd=md(2πfd)2,其中fd为等效单颗粒阻尼器的频率,MASRI等[18]建议fd≥20fs,本文取fd=20fs。等效颗粒阻尼器的阻尼系数cd=2mdξd(2πfd),其中ξd为等效颗粒阻尼器的阻尼比,该值与材料恢复系数相关[19],本文颗粒阻尼器采用恢复系数为0.5的钢,对应的阻尼比为0.2。由颗粒阻尼器提供的阻尼力可以表达为:

Fd=cdH+kdG

(2)

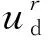
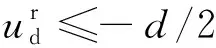
(3)

H=G=0

(4)

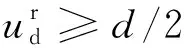
(5)

对于安装了底部固定型颗粒阻尼器的单自由度结构而言,其结构运动方程可以表达为:

(6)

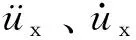
对于单自由度结构-底部固定型颗粒阻尼器体系,其结构运动方程为:

(7)

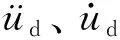
2.2 底部旋转型颗粒阻尼器的计算模型

根据底部旋转型颗粒阻尼器的工作原理,可将其视作两自由度的体系,包含一个水平自由度和一个转动自由度。结构-底部旋转型颗粒阻尼器体系的变形-受力图如图3所示。

图3 结构-底部旋转型颗粒阻尼器体系变形-受力图Fig. 3 Deformation-force diagram of structure-bottom rotated type particle damper system

相应地,结构-底部旋转型颗粒阻尼器体系的运动方程可表达为:

(8)

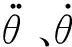
Fx=Fdcosθ

(9)

M=(-mdügcosθ+mdgsinθ-Fd)·D/2

(10)

式中:Fd=cdH+kdG,H和G的表达式为:

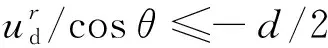
(11)

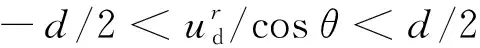
H=G=0

(12)

(13)

当θ=0时,式(11)～式(13)与式(3)～式(5)相同。

根据图3,等效颗粒的运动方程为:

mdüd/cosθ=-mdügcosθ+mdgsinθ-Fd

(14)

式(14)可改写为:

üd=-ügcos2θ+gsinθcosθ-Fdcosθ/md

(15)

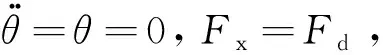
结构-底部旋转型颗粒阻尼器体系的分析流程图,如图4所示。

图4 结构-底部旋转型颗粒阻尼器体系的分析流程图Fig. 4 Flowchart of analyzing structure-bottom rotated type particle damper system

2.3 底部旋转型颗粒阻尼器的参数影响分析

基于2.1节和2.2节的公式推导,对不安装阻尼器的单自由度结构(无控结构)、有控结构1(安装底部固定型颗粒阻尼器)及有控结构2(安装底部旋转型颗粒阻尼器)进行谐振分析。

首先定义一个基准模型,结构参数取值:ms=103kg,ks=3.95×104N/m,cs=251.33 N·s/m,结构频率fs=1 Hz,阻尼比ξs=0.02。对于颗粒阻尼器,定义质量比η(阻尼器质量与主体结构质量的比值)为3%,则md=30 kg,ρ=7800 kg/m3,ρd=0.6,d=0.0216 m,fd=20 Hz,ξd=0.2,kd=4.74×105N/m,cd=1.51×103N·s/m,l=1 m,kr=5×104N/m,ls=0.1 m,mt取0.1%的ms。结构受到üg=Asin(2πft)m/s2的激励,幅值A=1,激励频率f=1 Hz。基于图4的流程图,采用常平均加速度法进行求解运动方程,时间积分步长取10-3s。

基准模型的位移和加速度时程曲线如图5所示,由图可知,相对于无控结构,有控结构1、有控结构2的结构响应明显降低,有控结构2的减振效果优于有控结构1。有控结构1位移和加速度峰值的减振率分别为16.2%和16.2%,而有控结构2对应的减振率分别为37.7%和37.4%。这说明对于基准模型,底部旋转型颗粒阻尼器的减振效果明显优于底部固定型颗粒阻尼器。

图5 基准模型位移和加速度时程曲线Fig. 5 Displacement and acceleration time history curves of benchmark model

通过调整基准模型的部分参数,考虑质量比η、激励幅值A、旋转刚度kθ及频率比等4个参数的变化对阻尼器减震性能的影响。

2.3.1 质量比

根据已有研究[10-11,14,20],质量比为影响颗粒阻尼器减振率的一个重要因素,质量比取值范围为1%～5%。质量比对阻尼器减振率的影响如图6所示。由图可知,对于某一特定的颗粒阻尼器,其位移和加速度减振率比较接近;2种颗粒阻尼器的减振率均随质量比增加而增加,其中,底部固定型颗粒阻尼器表现出明显的线性关系,而底部旋转型颗粒阻尼器呈现出近似的线性关系;底部旋转型颗粒阻尼器的减振率均高于底部固定型颗粒阻尼器,当质量比较大时,优势更显著。

图6 质量比对减振率的影响Fig. 6 Influence of mass ratios on vibration reduction ratios

2.3.2 激励幅值

激励幅值的大小影响颗粒阻尼器的振动程度,激励幅值取值范围为0.1～10 m/s2。图7为不同激励幅值下2种颗粒阻尼器的减振率对比。可以看出,对于某一特定的颗粒阻尼器,其位移和加速度减振率比较接近;当幅值增加时,底部固定型颗粒阻尼器减振率变化不大,但是底部旋转型颗粒阻尼器的减振率先升后降;当激励幅值较小时,底部旋转型颗粒阻尼器的减振率优于底部固定型颗粒阻尼器,而随着激励幅值的增加,底部旋转型颗粒阻尼器的减振效率可能会低于底部固定型颗粒阻尼器。这也说明,底部旋转型颗粒阻尼器对激励幅值的变化更加敏感。

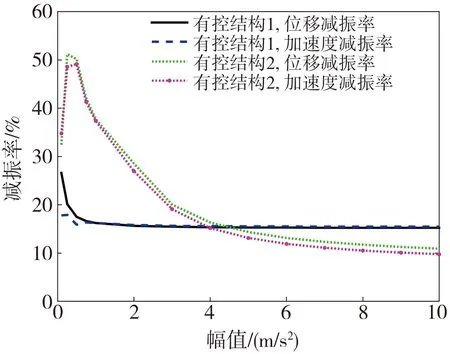
图7 激励幅值对减振率的影响Fig. 7 Influence of excitation amplitudes on vibration reduction ratios

2.3.3 旋转刚度

如前所述,旋转刚度是区别2种颗粒阻尼器的一个重要参数,当旋转刚度趋于无穷大时,底部旋转型颗粒阻尼器将退化为底部固定型颗粒阻尼器。考虑到旋转刚度kθ是弹簧刚度kr和弹簧间距ls的函数,因此保持弹簧间距不变,通过调整弹簧刚度kr来确定不同kθ对阻尼器减振率的影响,弹簧刚度kr取值范围为5×103～5×105N/m。不同旋转刚度(弹簧刚度)下阻尼器减振率的变化,如图8所示。对于底部固定型颗粒阻尼器,由于底部不具有旋转机构,所以旋转刚度的变化对其减振率没有任何影响,而对于底部旋转型颗粒阻尼器,其减振率随旋转刚度的增加有先增长后降低的趋势,这说明旋转机构过柔或者过刚都不利于其减振效果的充分发挥,需要设定合适的旋转刚度方可达到最佳减振率。此外,由图8可知,随着旋转刚度的增加,2种阻尼器的减振率越来越接近,这说明了旋转机构足够刚的话,底部旋转型颗粒阻尼器将会退化为底部固定型颗粒阻尼器。

图8 旋转刚度对减振率的影响Fig. 8 Influence of rotational stiffness on vibration reduction ratios

2.3.4 频率比

本节进行颗粒阻尼器的频率敏感性分析,通常的做法是考虑阻尼器频率与结构频率的比值(fd/fs)和激励频率与结构频率的比值(f/fs)2个值对阻尼器减振率的影响。由于颗粒阻尼器的频率通常取fd=20fs,即fd/fs为定值,因此本文仅考虑频率比f/fs对减振率的影响,频率比的取值范围为0.9～1.1,保持fs不变,通过改变激励频率f来实现频率比的变化。图9为不同频率比下2种阻尼器的减振率对比。由图9可知,2种阻尼器和TMD一样有频率敏感性较高的问题。当频率比小于1时,2种阻尼器减振率甚至可能为负,无疑对减振不利。此外,在不同频率比下,底部旋转型颗粒阻尼器的减振效果仍要优于底部固定型颗粒阻尼器。

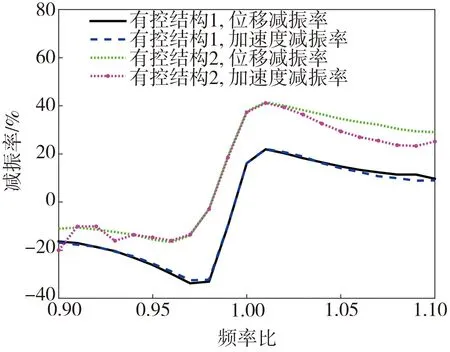
图9 频率比对减振率的影响Fig. 9 Influence of frequency ratios on vibration reduction ratios

3 多层框架结构减震分析

3.1 结构、阻尼器参数及地震动

选取文献[14]中的试验结构作为研究对象,该结构为5层钢框架,每层质量均为1200 kg,首层到顶层的侧向刚度分别为504660、558390、579430、579420、606430 N/m,根据特征值分析得到结构前3阶周期分别为1.04、0.35、0.22 s,采用瑞利阻尼,第一阶和第二阶阻尼比为0.0025。

结构顶部布置12个完全相同的多颗粒阻尼器,每一个阻尼器包括15颗直径为51 mm的钢球,每一个阻尼器的质量md=8 kg,ρ=7800 kg/m3,ρd=0.25,d=0.2085 m,fd=19.3 Hz,ξd=0.2,kd=1.18×105N/m,cd=388.1 N·s/m,容器的总质量mt=40 kg。在计算阻尼器提供的阻尼力时,需要将单个阻尼器产生的阻尼力乘以12。对于底部旋转型颗粒阻尼器,其旋转机构的参数设定为:l=1 m,ls=0.1 m,kr=5×105N/m。为了考虑地震动的随机性,选取El Centro波、Taft波、Kobe波、Northridge波和上海人工波(SHW2)等5条具有不同频谱特性的地震动输入,地震动的加速度时程曲线及频谱曲线如图10所示。在进行时程分析时,地震动均调幅至0.2g。

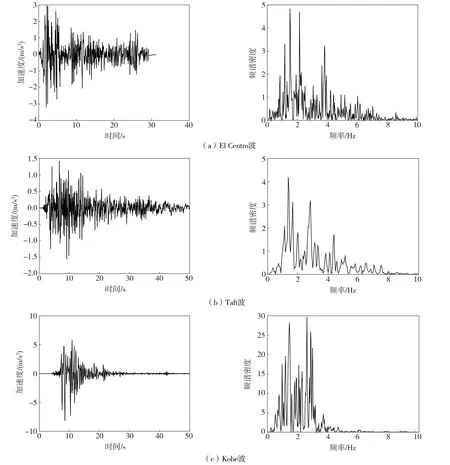
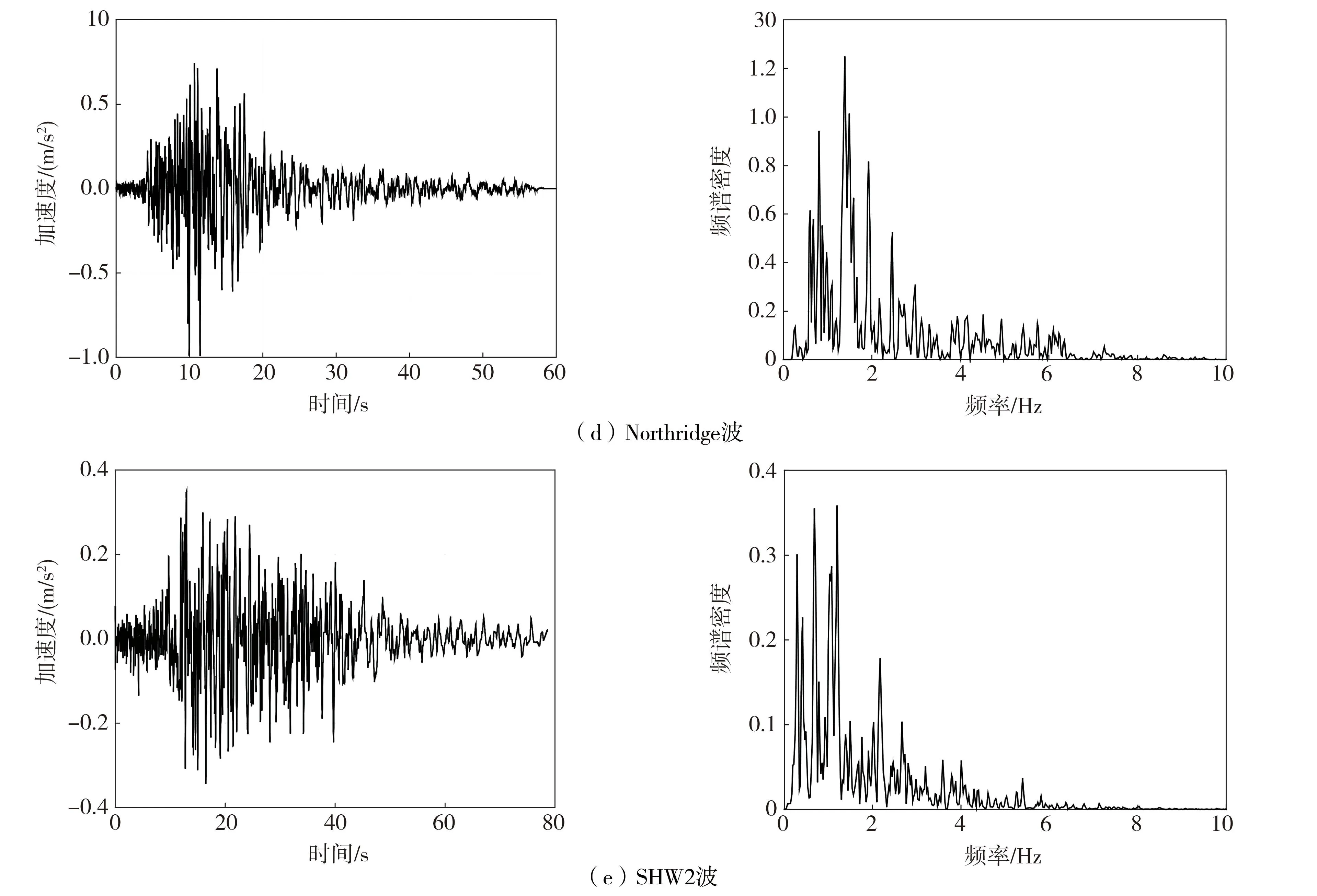
图10 地震动加速度时程曲线及频谱曲线Fig. 10 Acceleration time history curves and frequency spectrum of ground motions

3.2 阻尼器减震效果分析

图11给出了El Centro 波作用下无控结构、 有控结构1和有控结构2的顶层位移和加速度时程曲线。

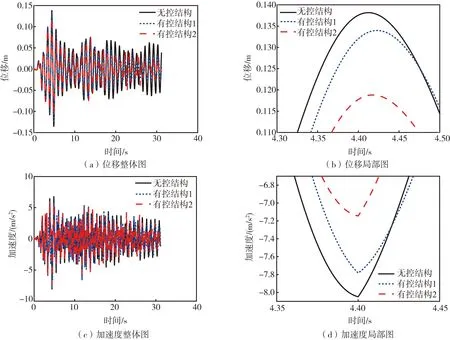
图11 顶层位移和加速度时程曲线Fig. 11 Displacement and acceleration time history curves of top story

对于底部固定型颗粒阻尼器,其位移和加速度的峰值减振率分别为6.86%、-11.67%,而底部旋转型颗粒阻尼器对应的减振率分别为32.55%、21.81%。不难发现,底部旋转型颗粒阻尼器的减震效果优于底部固定型颗粒阻尼器。图11中局部地方存在有控结构的响应放大现象,这是由于颗粒阻尼器存在频率敏感性问题。限于文章篇幅,其余地震动下的结构响应不在文中给出。不同地震动输入下2种颗粒阻尼器的位移和加速度减振率如表1所示。

表1 阻尼器减振率对比Table 1 Comparison of vibration reduction ratios of dampers %

由表1可知,在5条具有不同频谱特性的地震动作用下,底部旋转型颗粒阻尼器的位移和加速度减振率均优于底部固定型颗粒阻尼器,说明底部旋转型颗粒阻尼器具有较好的适用性。

4 结论

通过对本文提出的底部旋转型颗粒阻尼器进行参数影响分析和多层框架结构减震分析,并与底部固定型颗粒阻尼器进行对比,可以得到以下结论:

1)质量比是影响颗粒阻尼器减振性能的重要因素,底部旋转型颗粒阻尼器的减振率与质量比为近似线性正相关;在几种不同质量比的工况下,底部旋转型颗粒阻尼器的减振率均高于底部固定型颗粒阻尼器,当质量比较大时,优势更加显著。

2)激励幅值对底部旋转型颗粒阻尼器的减振率也有影响,随着激励幅值的增大,减振率先增后减,在一定的激励幅值范围内,底部旋转型颗粒阻尼器的减振率优于底部固定型颗粒阻尼器。

3)选择合理的旋转刚度对发挥底部旋转型颗粒阻尼器的减振效果至关重要,过柔或者过刚都不能充分发挥其作用;当旋转刚度趋于无穷大时,底部旋转型颗粒阻尼器将退化为底部固定型颗粒阻尼器。

4)2种颗粒阻尼器和TMD一样有频率敏感性较高的问题,在不同频率比下,底部旋转型颗粒阻尼器的减振效果仍要优于底部固定型颗粒阻尼器。

5)用于多层框架结构减震时,与底部固定型颗粒阻尼器相比,底部旋转型颗粒阻尼器减震性能更优。