一类具有信息干预的SEPAIRM模型的动力学分析与最优控制
黄怀玉,向会立
(湖北民族大学 数学与统计学院,湖北 恩施 445000)
传染病一直是人类生命安全和生态安全的巨大威胁,如何预防和控制传染病的传播一直是人们重要研究方向之一。建立贴近现实的数学模型对于更有效地预防和控制传染病具有重大的意义。如在现实生活中许多疾病都存在无症状感染[1-2],而忽略了无症状传播的影响将造成不必要的损失。Duong等[1]对登革热病毒传播的研究表明无症状感染者对蚊子的传染性明显高于有临床症状的患者,研究结果从根本上改变了当时对于登革热流行病学的认识和控制的模式。Hao等[3]通过病毒样本模拟了COVID-19的传播,推断具有大量的无症状和症状前传播,建立一类具有症状前感染和无症状感染的传染病模型。在对传染病传播行为有一定的基础之后,就需要采取一定的方法预防或者控制疾病的传播,而最优控制是重要的方法之一。Abbasi[2]提出了一个无症状感染区和隔离区的传染病模型的最优控制问题研究并应用到了新冠肺炎的研究。Saha等[4]提出了一个新的新冠模型的最优控制问题,即维持社会分化和疫苗接种程序随时间的变化,结果表明,只有接种疫苗才能显著降低整体感染人群。值得注意的是,媒体报道一直是预防和控制传染病的重要措施[5-8]。Rai[7]提出了一个数学模型来评估社交媒体广告对印度抗击病毒大流行的影响,他们的结果表明媒体覆盖是一种很重要的手段,为了彻底消灭疾病,应该提高认识水平,努力改变易感人群的行为。Buonomo 与Marca[8]提出了一种包括所有年龄段有效疫苗接种的行为流行病模型,疫苗接种依赖于信息。他们的结果表明地方性平衡点在R0>1与R0<1时都可能发生Hopf分叉。现实中疫苗是预防传染病传播最主要的措施之一,而加强人群意识,促使易感人群尽快接种疫苗也与媒体覆盖的强度有关。本文以受媒体信息影响的疫苗接种作为一种预防措施,通过加强媒体覆盖的强度,进而提高接种率,从而达到控制疾病传播的目的。本文在文献[3]的基础上考虑了媒体覆盖的因素,建立了如下模型:
(1)
其中:S, E, P, A, I, R, M分别是易感者,暴露者,症状前感染者,无症状感染者,症状感染者,移除者,媒体信息水平。Λ是招募率,w是无症状感染者和症状前感染者的传播率,b是症状传播者的传播率,μ1是移除率,在某一时刻,暴露者转移到症状前感染者的比率是de,症状前感染者到无症状感染者的比率是(1-r)dp, 症状前感染者到症状感染者的比率是rdp,无症状感染者,症状感染者到移除者的比率分别是da,di。δ代表媒体对于感染总数的反应率,μ2代表媒体传播中的信息损失率。参数Λ,w,b,r,de,dp,da,di,μ1,μ2,δ都是大于0的常数。
系统(1)初值条件为:
S(0)>0,E(0)>0,P(0)>0,A(0)>0,I(0)>0,R(0)>0,M(0)>0。
1 解的非负性与有界性
本节我们将验证系统(1)解的非负性和有界性。
定理1 系统(1)的解是非负的。
证明由系统(1)的第一个式子可得
(2)
其中
即
(3)
对(3)两边从0到t积分可得
(4)
由于S(0)>0, 所以S(t)非负。同理可以证明E(t),P(t),A(t),I(t),R(t),M(t)都是非负的。
定理2 系统 (1) 的解有界。
证明由系统 (1) 第一个和第二个式子可得
(5)
故
(6)
由定理1可得,S(t),E(t)非负, 所以我们得出S(t),E(t)有界,同理我们得出P(t),A(t),I(t),R(t),M(t)有界。
2 基本再生数与稳定点
接下来为了研究无病平衡点和地方性平衡点的稳定性,本节我们将首先证明无病平衡点和地方性平衡点的存在性并给出基本再生数的表达式。
2.1 无病平衡点
引理1 系统(1)存在唯一的无病平衡点
证明令系统(1)右端为0且I=0,可得
2.2 基本再生数
基本再生数是指在易感者人群中,一个感染者所可以传染的人数,它是判断疾病是否持续存在的关键阈值。根据文献[9],基本再生数R0计算公式如下:
(7)
引理2 当R0>1时,系统(1)存在唯一的地方性平衡点X*。
证明令系统(1)右端为0,I≠0,计算可得
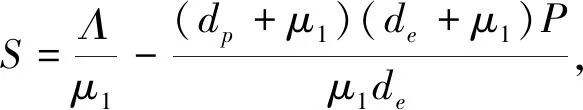
(8)
(9)
将这些公式带入系统(1)中可得

令
(10)
显然G(P)关于P是一个增函数,而当
R0>1时,
(11)
则由介值定理可得存在P*>0, 使得
G(P*)=0,
(12)
所以,系统(1)存在唯一的地方性均衡点X*=(S*,E*,P*,A*,I*,R*, M*), 其中

3 稳定性分析
本节我们将通过基本再生数R0研究无病平衡点和地方性平衡点的渐进稳定性。
3.1 无病平衡点的稳定性
定理3 当R0<1时,无病平衡点X0是局部渐进稳定的。
证明非线性系统(1)在无病平衡点X0处的雅可比矩阵为
(13)
其中
g=wS0,d=bS0。
故J(X0)对应的特征方程为
(α+μ1)2(α+μ2)T(α)=0,
(14)
其中
T(α)=(α+de+μ1)(α+dp+μ1)(α+da+μ1)(α+di+μ1)
gde(α+di+μ1)(α+da+μ1)
-g(1-r)dedp(α+di+μ1)
-drdedp(α+da+μ1),
显然α1=α2=-μ1,α7=-μ2是特征方程(14)的特征根且都具有负实部。下面我们将证明剩余的根具有负实部。不妨假设α=x+iy(x,y∈R)是特征方程(14)的一个特征根且x>0,则
=R0,
这与R0<1矛盾,故特征方程(14)的每个根都具有负实部。因此当R0<1时,无病平衡点X0是局部渐进稳定的。
3.2 地方性平衡点的稳定性
定理4当R0>1时,若满足
则地方性平衡点X*具有局部渐进稳定性,其中取
n=

a=(da+μ1),p=(dp+μ1),e=(de+μ1),i=(di+μ1),m=(l+μ1),
A1=m+p+a+i+μ2+e,
A2=l(p+a+i+μ2+e)+p(a+i+μ2+e)+a(i+μ2+e)+i(μ2+e)+μ2e,
A3=eμ2(i+a)+ai(e+μ2)+p(μ2e+ie+iμ2+ae+aμ2+ai)+l(eμ2+ie+iμ2+pa)+
l(ae+aμ2+ai+pμ2+pa)+
g*de(l+μ2+μ1+i+a)+deq*(l+μ2+μ1+i+p)+deq*(1-r)dp+rdpdeq*+ndeδ,
A4=eiμ2(a+p)+paμ2(e+i)+μ2l(ei+ea+ai)+pl(μ2e+μ2i+ia+aμ2+ae)+
deg*(l(i+μ2+a)+μ2(i+a)+ia)+qdedpdp(1-r)(l+μ2+i)-q*del(μ2+a+i)-
nδdel+ndeδ(dp-2rdp+i+a+l)+r2ded*dp(l+μ2+a),
A5=μ2ei(ap+la+lp)+lpa(eμ2+ie+iμ2)-nδ(i+a)del+
deg*(lμ2(i+a)+il(a+μ2)+al(μ2+i))+q*dpde(1-r)(l(μ2+i)+μ2i)+
rdpded*(l(μ2+a)+μ2a)-g*del(μ2(i+a)+ia)-nrplδd*de+
ndeδ[dp(1-r)(l+i)+rdp(a+l)+ai+il+al]-n(1-r)dpdelδ,
A6=aielpμ2+iaμ2delg*+il(1-r)dpdeg*μ2+raμ2lded*dp-ialg*deμ2-
nralδdpde-nilδ(1-r)dpde-niaδlde+ndeδ[(1-r)dpil-rdpam+ial],
证明非线性系统(1)在地方性平衡点X*的雅可比矩阵为
(15)
则J(X*)对应的特征方程为
(α+μ1)(α6+A1α5+A2α4+A3α3+A4α2+A5α+A6)=0,
(16)
显然α1=-μ1是特征方程(16)的一个特征根且具有负实部。经过计算可得A1>0,A2>0,A3>0,A4>0,A5>0,A6>0。由Routh-Hurwitz准则知,如果R0>1,且满足
A1A2>A3,
则地方性平衡点X*是局部渐进稳定的。
4 最优控制
为了有效控制疾病的传播,本文考虑易感人群受媒体信息依赖的疫苗接种,以及通过治疗来降低传播者人数来控制病毒传播,在系统(1)中引入两个控制变量,u(t)代表媒体信息报道的强度,v(t)代表对感染人群的治疗强度,建立了如下的最优控制系统:
(17)
其中:p0代表接种疫苗后基本接种率的正常数。
允许控制集为:
Uad={u,v|0≤u≤1,0≤v≤1,u,v是可测函数}
在对传染病的预防控制中,人们希望尽可能降低因为疫苗接种,感染治疗与通过媒体覆盖而产生的经济与时间成本。为此,定义最优目标泛函为:
(18)
式中:k1,k2,n1,n2是相应的权重系数。
4.1 最优控制的存在性
在这一节中,我们将首先证明最优控制的存在唯一性。
定理5 对系统(17),存在唯一的最优控制对(u*,v*)和所对应的(S*,E*,P*,A*,I*,R*,M*),使得
(19)
证明为了证明最优控制的存在唯一性,应用文献[10]的结果。主要分为以下几步:
1)允许状态集非空;
2)允许控制集Uad是凸且闭集;
3)系统(17)的右侧被状态和控制变量的线性函数所限定;
4)被积函数
是凸函数。
5)存在常数η1>0.η2>0,η3>0 使得被积函数L满足
现在来逐个验证以上5项:
1)由定理2方法可得,系统(17)的右端有界, 进一步由系统(17)右端是连续的,所以根据文献[11]得,系统(17)至少存在一个解,因此允许状态集非空。
2)任意U1,U2∈Uad及λ∈[0,1],其中U1=(u1,v1),U2=(u2,v2),取U3=λU1+(1-λ)U2,则
U3=(u3,v3)=(λu1+(1-λ)u2,λv1+(1-λ)v2)
由0≤ui≤1且0≤vi≤1(i=1,2),故u3∈[0,1],v3∈[0,1],故U3∈Uad,即U是凸集。另一方面,若Un=(un,vn)∈Uad(n∈N+),且
由0≤un≤1,0≤vn≤1,可得0≤u≤1,0≤v≤1且u,v是可测函数,故Uad是闭集。
3)由0≤u≤1, 0≤v≤1,从而通过系统(17),我们可知
(20)
其中:K1,K2的值由系统(17)决定, 因此(3)成立。
4)显然被积函数是凸集,在此便不过多证明。
5)取
则
4.2 最优控制的特征
在这一部分,我们将研究通过Pontryagin最大值原理研究最优控制及其协态变量的表达式。为此,我们定义系统(17)的拉格朗日算子为
(21)
及所对应的哈密顿函数
(22)
定理6 在系统(17)中,对最优控制对(u*,v*)与状态变量(S*,E*,P*,A*,I*,R*,M*)存在相应的协态变量(λ1,λ2,λ3,λ4,λ5,λ6,λ7) 且
(23)
所对应的横截条件为
λ1(T)=0,λ2(T)=0,λ3(T)=0,
λ4(T)=0,λ5(T)=0,λ6(T)=0,λ7(T)=0。
此外最优控制变量u*,v*的表达式为:
(24)
其中,
证明将(17)代入(22)式可得:
λ4((1-r)dpP-daA-μ1A)+
λ7(δ(P+A+I)-μ2M)。
对任意t∈[0,T], 根据Pontryagin最大值原理,那么存在协态变量λ1,λ2,λ3,λ4,λ5,λ6,λ7,满足
故得出式(23)。
根据最优条件,当u=u*,v=v*时,
经过计算得出
(24)
根据允许控制集的定义, 有
(25)
5 数值拟合
5.1 敏感性分析
敏感性分析揭示了每个参数对疾病传播的重要性,这些信息对研究传染病模型的非线性动力学行为至关重要,对如何控制和预防疾病传播,如何采取有效而又经济的控制措施都具有重要的意义。敏感性分析主要分为两种,一种是局部敏感性分析,一种是全局敏感性分析。局部敏感性分析主要通过每次改变一个输入参数,同时将其他参数保持在中心值来检查输出的局部影响,而全局敏感性(见文献[12])分析则是通过大范围扰动模型输入参数,从而量化模型输入对输出的影响。本文主要通过全局敏感性分析来评价参数对基本再生数的相对重要性。
利用超立方采样(Latin hypercube sampling, LHS)计算各参数,并用这些参数的局部秩相关系数进行全局敏感性分析。选取参数Λ=1,μ1=0.05,b=0.40,w=0.55,r=0.23,de=0.35,dp=0.43,da=0.35,di=0.35,可以得出不同R0的局部秩相关系数值,如图1所示。
由图1可知,参数μ1,da,dp对基本再生数R0有消极影响,de,r,dp,S0,b,w对基本再生数R0有积极影响。值得注意的有以下几个方面:第一,疾病传播率依然是影响最大的因素,其中包括无症状感染者的传播率与症状传播者的传播率,无症状感染的传播率影响稍大这也符合实际,这提醒人们应该提高自身安全意识,避免无症状感染。第二,易感者的人数对于基本再生数的影响也比较大,这代表在不同人口基数的城市,病毒传播的速率可能大有不同。第三,考虑到疾病传播函数与易感者人数和传播率有关,通过媒体覆盖的影响改变易感者的行为从而延缓病毒的传播非常重要。
5.2 稳定性分析
在式(7)中,选取参数Λ=1,μ1=0.01,μ2=0.05,b=0.007,w=0.55,r=0.23,de=0.35,dp=0.43,da=0.35,di=0.35, 此时R0=0.02,S0=100,图2和图3验证了定理3,无病平衡点是渐进稳定的。
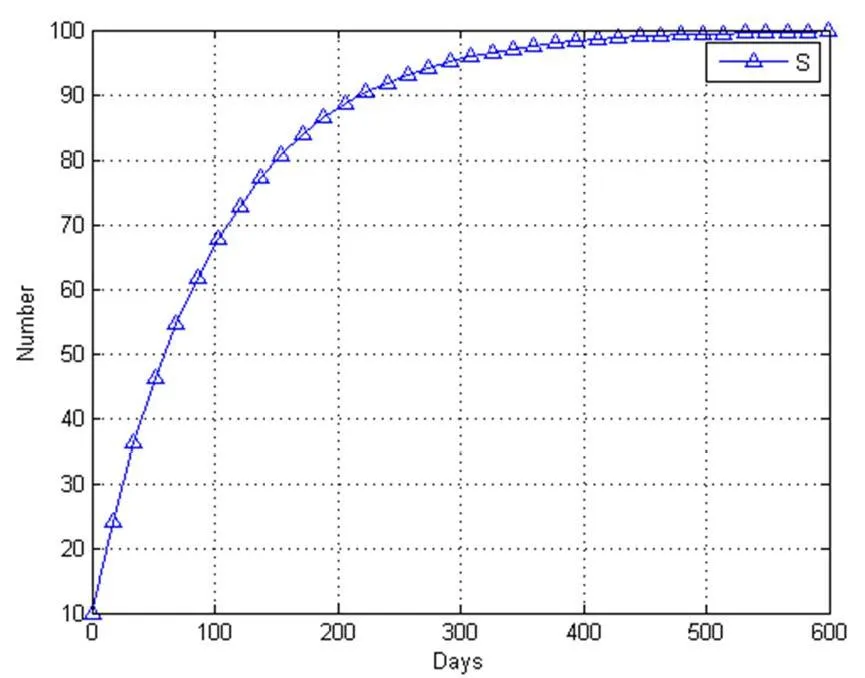
图2 R0=0.02时,S(t) 随时间变化
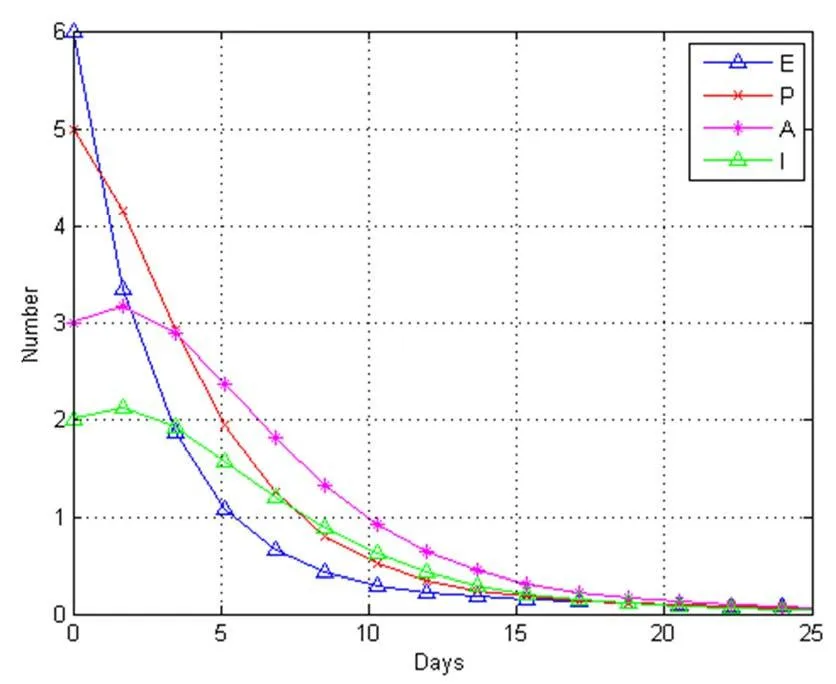
图3 R0=0.02时,E(t),P(t),A(t),I(t) 随时间变化
由图3可知,无症状感染者和症状感染者都将经历一个短暂的上升再迅速下降,这个现象说明即便R0<1,在一段时间内,感染人数依旧会增加,所以在疾病出现,还是应当注意防护。其他参数保持不变,将b取为b=1.27,可得R0=4.04。
利用图4和图5,可以验证引理2和定理4,当R0>1时, 存在一个地方性平衡点,而且这个地方性平衡点是渐进稳定的。

图4 R0=4.04时,S(t) 随时间变化随时间变化

图5 R0=4.04时,E(t),P(t),A(t),I(t)随时间变化
由图5可知,无症状感染者和症状感染者都将经历一个上升的阶段后逐步稳定,但是无症状感染者上升稍稍快一点,这可能与无症状传播的隐蔽性有关。
5.3 最优控制
通过bvp4c 函数法进行模拟,取Λ=1,μ1=0.01,μ2=0.05,b=1.27,w=0.55,r=0.23,de=0.35,dp=0.43,da=0.35,di=0.35, 得到了最优控制函数图(图6和图7)。
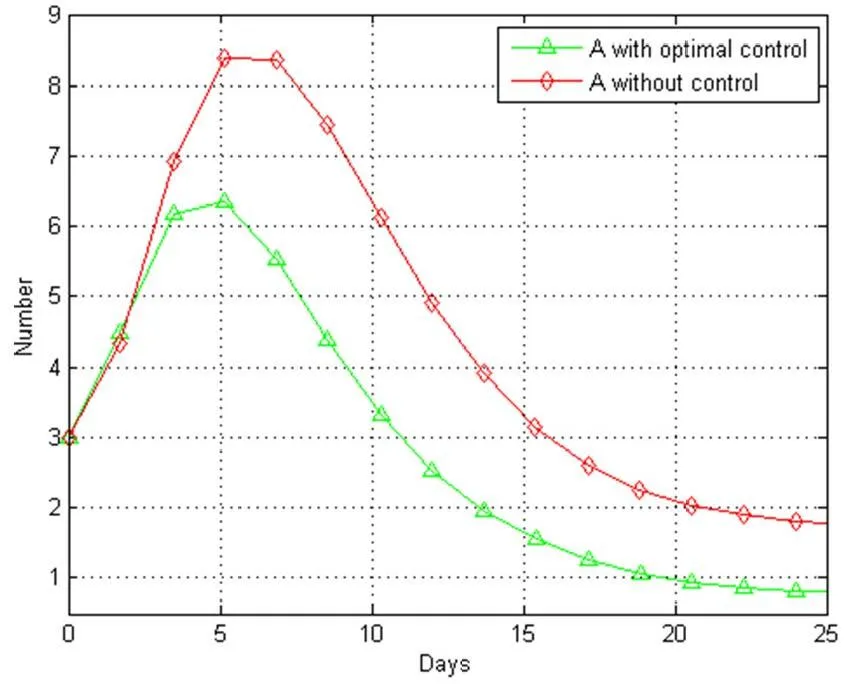
图6 无症状感染者

图7 症状感染者
由图6和图7可知,在加入最优控制策略之后,无论是无症状感染者还是症状感染者人数都将发生显著的下降,但是症状感染者的下降最为明显,这说明加强治疗措施非常有效,因为在现实生活中,症状感染者的治疗与恢复非常重要。从另一角度考虑,治疗措施主要针对的是症状感染者,那么对于预防控制无症状传播,加强媒体覆盖的强度这一措施就尤为重要。
由图6可知,无症状感染者人数虽然最终也会得到很大程度的控制,但是依然会上升一段时间,这与现实生活中,无症状感染者的隐蔽性也是符合的。而由图8与图9可知,一方面间歇性的信息覆盖比较合理,一方面在感染人数大幅度下降之后,应该继续保持一段时间的控制措施,以避免疫情再次上升。
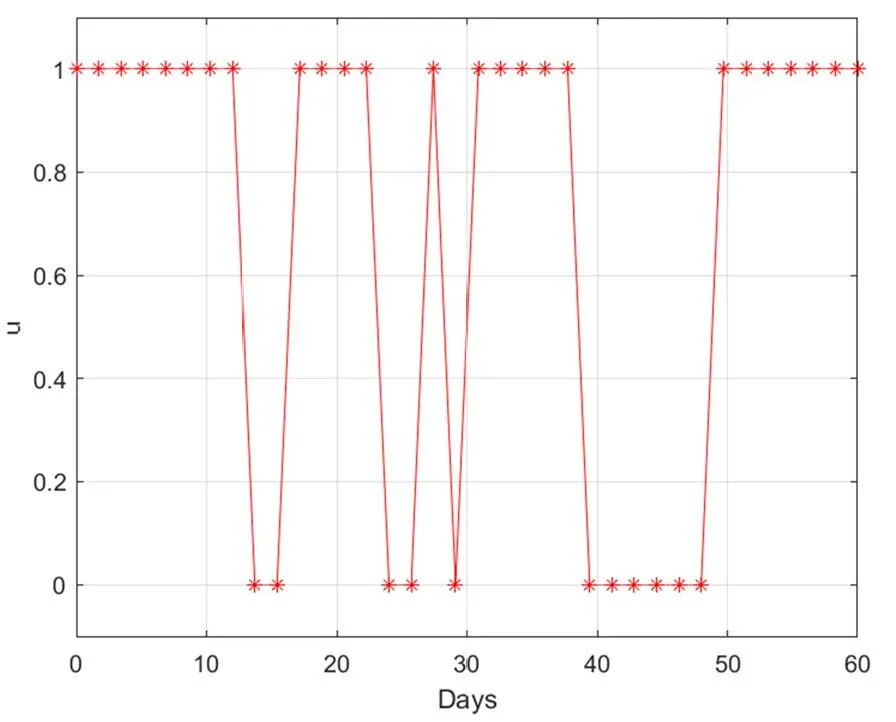
图8 信息强度(u)
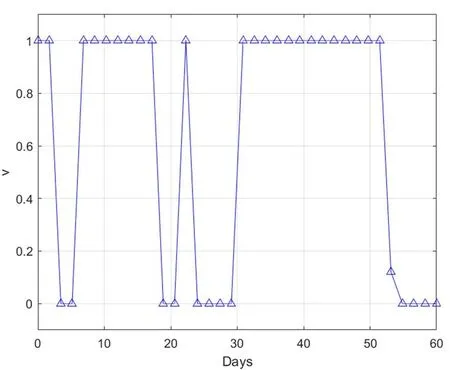
图9 治疗强度
6 结束语
本文考虑了媒体传播对于传染病传播的影响,建立了SEPAIRM 模型,推导了基本再生数R0,并且证明了当R0<1时, 系统的无病平衡点是局部渐进稳定的,当R0>1时,存在唯一的地方性平衡点,并且得出了地方性平衡点局部渐进稳定的条件。在最优控制研究中,通过Pontryagin最大值原理得出了最优控制变量的表达式。在最后的数值模拟中,验证了无病平衡点和地方性平衡点的稳定性,同时通过最优控制函数图也发现,最优控制策略对于降低感染人数是有效的,媒体覆盖对于预防控制无症状传播非常重要,而且间歇性的控制比较合适。

