基于FRFT-RBF网络的船舶电网故障定位方法
王高阳 刘 峰
(1.武汉船舶职业技术学院,湖北武汉 430050;2.中国船舶集团有限公司第六〇五研究院,广东广州 510250)
随着海洋强国战略的不断深化,各种复杂的海洋工程作业对船舶电力系统的可靠性和生命力提出了更高的要求。目前,大多数海洋工程船舶采用闭环设计、开环运行的理念将海洋工程船电网设计成环状型结构,从设计角度提高船舶电力系统的可靠性和生命力。但在运营方面,当船舶发生电网单相短路故障时,大多数船舶仅能由绝缘监测仪发出“绝缘低”报警信号,无法定位故障的具体区域,需要船员对线路进行逐条排查,耗费大量时间来完成故障的定位和修复,在一定程度上增加了船舶海上作业的风险。而实现船舶电网短路故障的智能定位则能降低这一风险,提高船舶电网生命力,且能有效提升船舶电力系统运行管理水平,提高船舶电网运行的可靠性。
针对电网故障定位的研究目前大多以陆地电力系统为对象,船舶电网的故障定位研究较晚,研究成果相对较少。陆地电网故障定位方法主要有阻抗法、行波法以及基于配电网自动化的方法等,船舶电网故障定位方法主要分为基于对故障信号的特征提取和基于对船舶电网运行状态的监测两大类。
由于船舶电网规模和容量较陆地电网小很多,建造成本也比较有限,在已建造投运的船舶中很少配备配电网自动化系统。根据表1 所述,基于故障信号处理的船舶电网故障定位方法不需要利用配网自动化系统,比较切合实际船舶的使用情况。由此,本文将针对船舶电网故障信号具有非平稳性的特点,采用故障信号处理法,对船舶电网单相接地故障特征提取和故障区域定位方法展开研究。
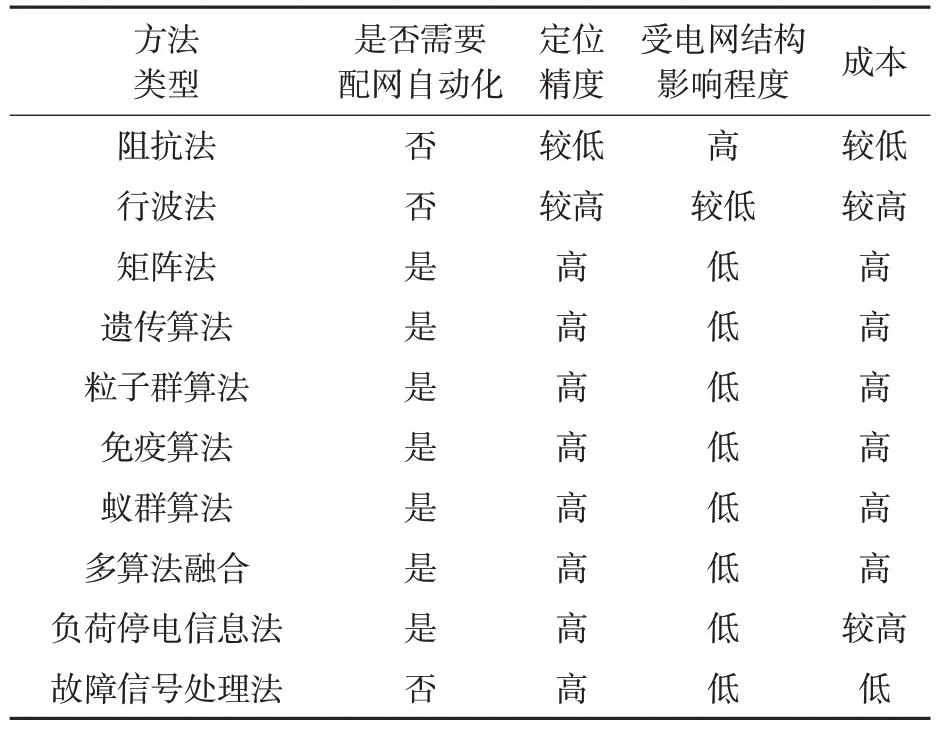
表1 现有的电网故障定位方法特点
1 基于FRFT的故障特征提取方法
故障信息的分析及特征提取是故障识别和定位的前提条件,当船舶电网故障后能在固定节点检测到电流或电压的波形变化,而对故障波形的信息进行分析和特征提取是完成故障定位的关键。船舶电网故障电流和电压信号通常具有非平稳性,常用的信号处理方法对其特征提取存在一定的局限性。
由于传统的傅里叶变换是一种线性算子,在分析信号时只能将时间轴逆时针旋转90°角到频率轴,与频率轴重合,得到的是信号的整体频谱,是一种全局性变换,无法表述信号的时频局部特征。而分数阶傅里叶变换(FRFT)的算子是可以旋转任意角度的算子,能得到信号新的表示,反映出局部的时频特征,因时频特征是非平稳信号最关键的性质,故非常适合采用分数阶傅里叶变换处理船舶电网电流、电压等非平稳信号。
1.1 分数阶傅里叶变换最优阶次的确定方法
信号在时频域的聚集性越强,其特征信息越显著,越有利于特征的提取和识别,分数阶傅里叶变换的最优阶次即为信号在时频域聚集性最好时对应的FRFT阶次。选取能量聚集效果最好的阶次,在其分数阶傅里叶变换域里具有显著的特征信息。
对于不规律信号或未知信号,常采用二维峰值搜索方法进行FRFT 最优阶次的确定。具体方法为:对阶数p 在某个范围内进行连续取值,将原始信号所在的时频域进行连续的旋转;同时对每一个阶次p的取值下的原信号进行分数阶傅里叶变换;然后将阶次p 所有取值对应的FRFT 能量峰值构成参数(p,μ)的二维分布;最后在参数(p,μ)的二维分布平面内搜索纵坐标最大的点,其对应的阶次p即为分数阶傅里叶变换的最优阶次。
最优阶次求解的二维峰值搜索法流程图如图1所示。
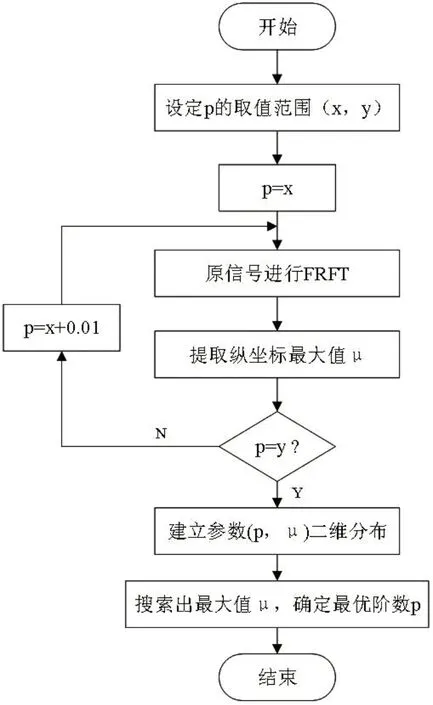
图1 二维峰值搜索法流程图
1.2 基于FRFT的信号滤波去噪处理方法
为了避免噪声对初始信号的干扰,需要对采集到的初始信号进行滤波去噪处理,滤除各种干扰噪声。传统的信号滤波去噪主要采用基于傅里叶变换的方法,通过信号的傅里叶变换和滤波函数的相乘计算完成滤波。但是,当信号遭受强烈的时频耦合干扰,在时频域的图像出现重叠时,传统的傅里叶滤波方法很难完成达到滤波效果。在这种情况下,由于分数阶傅立叶变换具有自由旋转因子的优势,可通过选择合适的坐标角度与信号匹配,将正常信号和干扰信号分离,解决时频耦合造成的干扰,达到滤波效果。
设定采集的信号x(t)中正常信号为y(t),噪声信号为n(t)。滤波的具体步骤如下:
(1)根据二维峰值搜索方法,估计阶次p 和对应频率u的取值。
(2)对采集的信号x(t)进行分数阶傅里叶变换,如式(2)所示。
其中,YP(u)为正常信号y(t)的p阶分数阶傅里叶变换,NP(u)为噪声信号n(t)的p 阶分数阶傅里叶变换。在FRFT 域,正常信号的能量具有聚集性,聚集在以u 为中心的窄带上,而噪声信号则不会出现能量聚集性。
(3)在FRFT域,按照式(3)对上一步形成的能量聚集尖峰进行遮隔处理。
其中,C(u)为FRFT 域中以u 为中心的带通滤波器,通过选择适当的带宽可将噪声信号有效的消除,输出能量采集信号的能量。
(4)将经过滤波去噪处理后的FRFT域信号进行-p 阶分数阶傅里叶变换,即p 阶分数阶傅里叶反变换,得到去噪的时域信号xout(t)。具体流程如图2所示。

图2 基于FRFT的信号滤波去噪处理方法示意图
1.3 基于功率谱和能量率的故障特征提取实现方法
船舶电网正常运行时,其电力参数是稳定的;当电网出现故障时,其电力参数会发生较大变化。由于故障与非故障之间、不同故障状态之间都将呈现出不同的功率和能量特征,本文将根据功率谱和能量率的理论,对故障特征提取方法展开研究。
功率谱的定义:假设某电力系统输出的一个原始信号x(t),经过数据转换、滤波操作等预处理后,则x(t)的FRFT域的功率谱定义如下:
式中,XP(u)是原始信号x(t)的分数阶傅里叶变换,N为采样的数据总点数。
能量率的定义:原始信号x(t)在分数阶傅里叶变换域的固定频带的能量率表示为:
将固定频带划分为若干个子频带,第i 个子频带的能量率为:
式中,(u)是原信号x(t)的第i 个子频带的功率谱,Ni表示第i个子频带的采样点数。
根据多用途工程船电网拓扑图模型可知,电网共有26条支路,当任何一条支路发生短路故障时,其所在支路的电流和电压信号均会发生变化,而将这种变化的特征提取出来,则能为故障的定位和识别提供数据支撑。基于上述功率谱和能量率的定义,可将电网故障信号的特征提取过程分为以下几步:
(1)对采集的原始信号x(t)进行预处理。首先对信号进行零线调整,去除因传感器漂移产生的零漂现象;然后按照FRFT域的滤波方法进行全局滤波,滤除各种干扰噪声,保留0 到1000Hz 的频带成分。
(2)将经过预处理的原始信号按最优阶次进行分数阶傅里叶变换,得到信号在分数阶傅里叶域内的频带。
(3)在FRFT 域范围内,选取部分频带作为特征提取的对象。令提取信号区段的横坐标u 取值范围为[0,fs] Hz。
(4)将提取信号片段按照横坐标为Δf 划分为若干个子频带,按照式(4)至(6)计算每个子频带对应的能量率。子频带的总数量为:
选取频带的功率谱对应的子频带对应的能量率为Ei( i=1, 2, 3,…, fs/Δf )。
(5)将选取频带对应的子频带按顺序组合成能量率特征向量,如式(8)所示。
(6)为了提高神经网络训练的准确性,对能量率特征向量中的元素按式(9)进行归一化处理,作为故障识别和故障定位神经网络的训练输入样本。
其中,x为处理后的数据,s为待处理数据,smax为向量中元素的最大值,smin为向量中元素的最小值。
2 基于RBF 神经网络的电网故障特征定位方法
完成船舶电网故障特征提取后,需要对特征识别才能实现故障定位。鉴于RBF(Radial Basis Function)神经网络是一种性能优良的前馈型神经网络,可以任意精度逼近任意的非线性函数,且具有全局逼近能力,拓扑结构紧凑,结构参数可实现分离学习,收敛速度快等特点。因此,本文采用RBF神经网络作为故障特征识别方法进行船舶电网故障定位。
RBF 神经网络包括1 个输入层、1 个隐层和1个输出层,其网络拓扑结构如图3 所示,输入层神经元个数为p,隐层神经元个数为n,输出层神经元个数为q。网络模型采用局部激励函数,其输入层和输出层神经元个数是确定的,隐层神经元个数在网络训练中自动调整,能有效提升最优解精度。

图3 RBF神经网络拓扑结构图Fig.3 Topology diagram of RBF Neural Network

图4 基于FRFT-RBF神经网络的船舶电网故障定位方法流程图
基于RBF神经网络的电网故障定位方法具体实现过程分为以下几个步骤:
(1)提取故障特征
按照基于FRFT的故障特征提取方法,提取船舶电网故障特征,得到故障特征向量。
(2)建立神经网络模型
按照故障特征向量的维数,设定神经网络模型的输入神经元的个数。
根据电网模型正常运行时的支路编号,设定神经网络模型的输出神经元个数为1,输出目标值与具体故障支路的编号一一对应。同时,确定隐层的神经元数量,将隐层层数设定为1,选定神经网络类型,完成神经网络模型的建立。
(3)训练神经网络
设定神经网络的最大训练步长及误差精度等参数,导入大量的故障特征向量进行神经网络的训练,将并将训练好的网络权值和偏差存至存储器中。
(4)定位船舶电网中的故障区域
导入船舶电网故障数据,利用训练好的神经网络进行故障区域定位,输出电网故障支路编号。
3 算例仿真
为了验证船舶电网故障特征提取方法的可行性,本文以某多用途工程船为背景,建立船舶电网模型,开展电网单相故障接地故障定位仿真实验。
3.1 船舶电网建模及故障仿真
某多用途工程船电力系统为交流三相三线绝缘系统,设置4 台发电机组,2 台变压器,8 个汇流排,26条支路。船舶电网按照闭环设计,开环运行的原则,正常运行时的电网结构如图5所示。
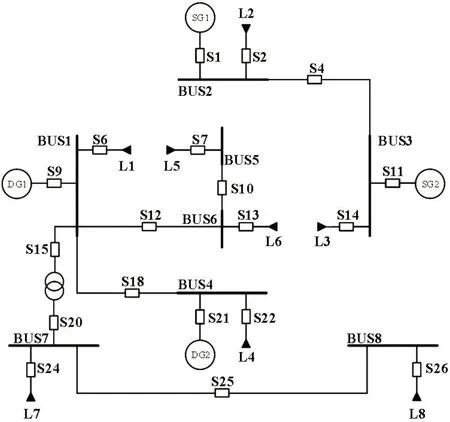
图5 多用途工程船电网正常运行结构图
其中,两台为柴油发电机组额定功率为400kW,两台轴带发电机额定功率为750kW,4台机组额定电压均为400V,频率为50Hz;两台变压器容量均为200kVA,在电网运行中为一用一备模式。在算例仿真中为了简化电网结构,将每条汇流排上的负载等效为一个综合负载,共8个综合负载,其参数如表2所示。电网中各支路阻抗值如表3所示。
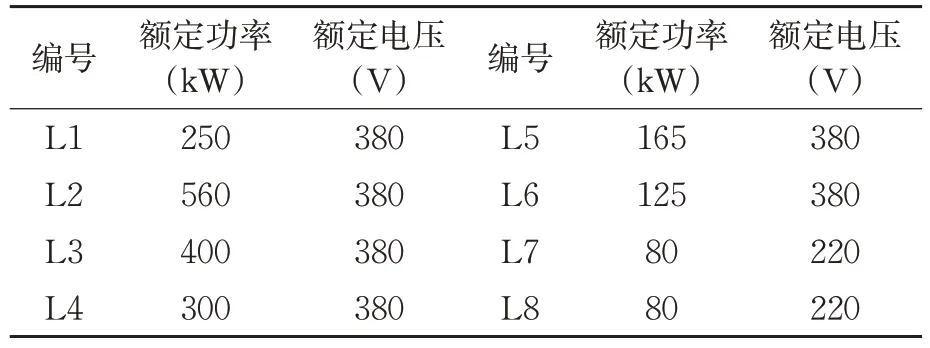
表2 负载额定参数一览表
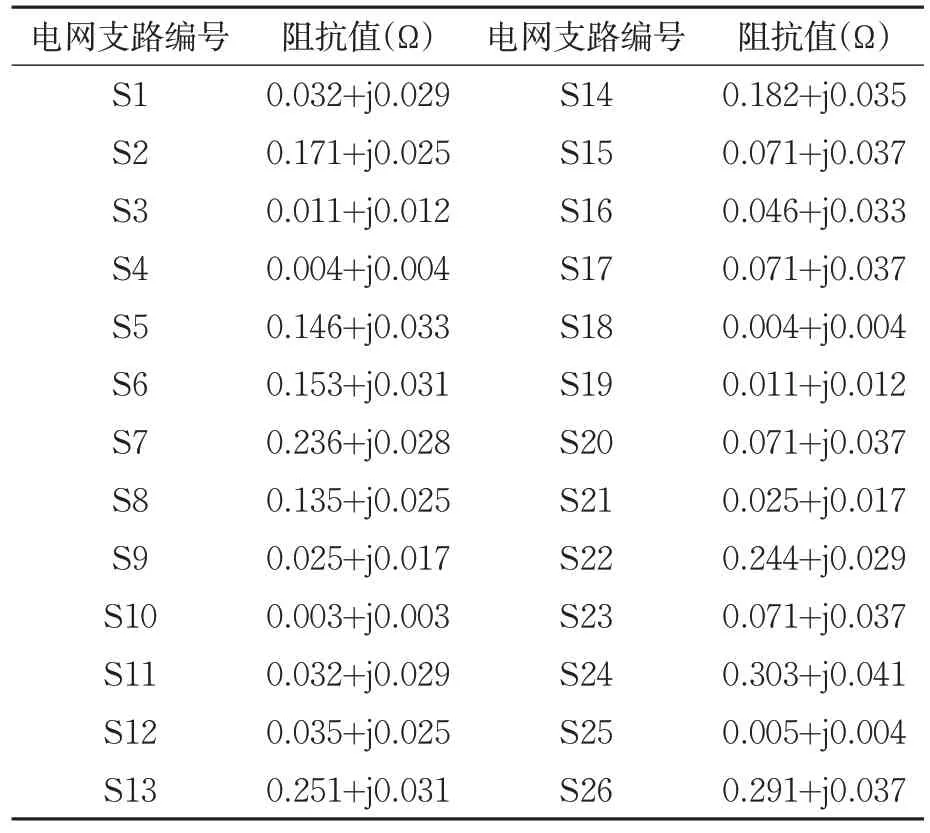
表3 电网各支路电力参数一览表
将S9 支路设置单相接地短路,并按基于FRFT的信号滤波去噪处理方法,对获取的故障电压波形进行滤波去噪处理,得到如图6所示的故障电压波形。

图6 S9支路单相短路故障电压波形
3.2 故障特征提取
按基于FTFR 的故障特征提取方法步骤,对S9支路故障电压波形进行故障特征提取。
3.2.1 获取故障电压FRFT域频谱图
设定分数阶傅里叶变换的阶次取值范围为p∈(0,2),将经过滤波后的S9支路故障电压信号按照阶次p依次进行分数阶傅里叶变换的数值计算,得到故障电压的FRFT域频谱图,如图7和图8所示。

图7 S9支路故障电压的FRFT域频谱三维分布图
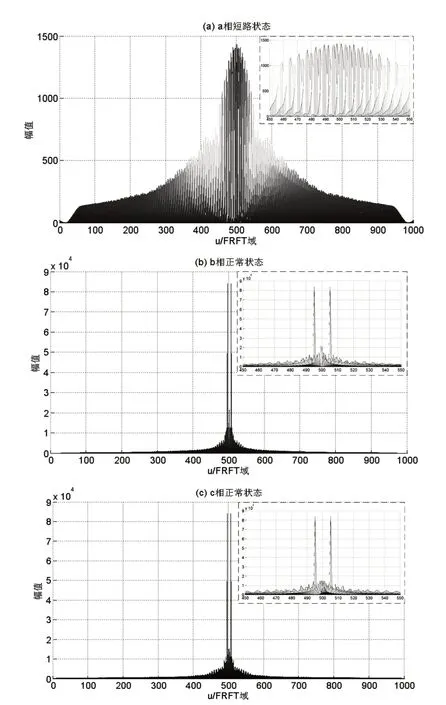
图8 S9支路故障电压的FRFT域频谱平面分布图
3.2.2 确定故障特征提取的频率范围
由图8 可知,S9 支路a 相、b 相和c 相电压FRFT 域频谱的峰值均主要集中在频率范围为450Hz 至550Hz 的区段,因此将频率范围为[450Hz,550Hz]的一段频谱作为故障特征提取对象,提取频谱段总长fs=100Hz。
3.2.3 确定最优阶次
按照基于二维峰值搜索的最优阶次求解方法,求得最优阶次p0=0.93,按照最佳阶次p0对S9支路故障电压进行FRFT变换,得到故障特征提取区段的FRFT域频谱图,如图9所示。将故障特征提取区段按照横坐标Δf 划分为若干个子频带,设Δf=10Hz,则每相有10 个子频段,三相共有30 个故障特征子频段。
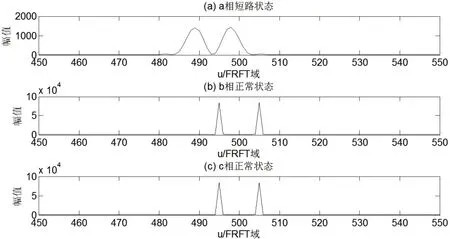
图9 S9支路故障电压的最佳阶次FRFT域频谱图
3.2.4 计算得到特征向量
按照式(4)~(6)对各子频段频谱进行能量率计算,得到如图10所示的能量率图谱。
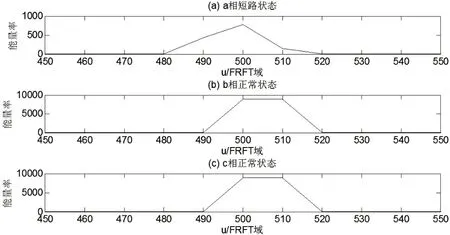
图10 S9支路故障电压的能量率图谱
按照a、b、c 相的顺序依次将每相故障特征子频段的能量率计算值组合形成特征向量,S9 支路故障电压的特征向量如表4所示。

表4 S9支路故障电压特征向量一览表
3.2.5 特征向量归一化
按照式(9)对表4 中的数据进行归一化处理后,将数据先按照每相的子频段序号排列,再按照a 相、b 相和c 相的顺序依次排列组合成30 维度的向量,即为S9 支路发生单相接地短路故障的一组特征向量。
3.3 电网故障定位
在获取船舶电网故障特征向量训练样本和实验样本基础上,搭建RBF神经网络模型,按照船舶电网故障特征向量的维数,设置输入层的神经元个数为30;按照故障可能发生的支路数量,设置输出层的神经元个数为1;隐层到输出层的激活函数采用Gaussian 函数。设置最大训练次数为1000 次,对RBF 神经网络模型进行训练。完成RBF 神经网络的训练后,再对多用途工程船电网正常运行状态的19 条支路分别进行3 次单相接地故障仿真和特征提取,将得到的57 组故障特征向量分别导入训练好的RBF神经网络进行电网故障定位验证实验,实验结果如图11 所示,实验误差分析如图12所示。

图11 基于RBF神经网络的电网故障定位试验结果图
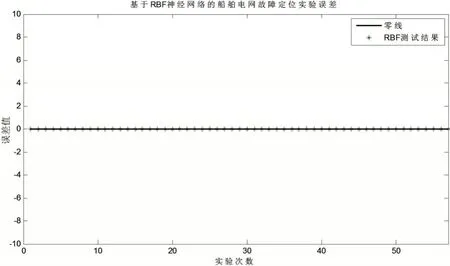
图12 基于RBF神经网络的电网故障定位实验误差分析图
在定位实验中,将误差小于0.5 作为定位成功的判别条件。由图12和表5所示的试验数据可知,57 组实验成功率100%,且误差能控制在0.01 以内,远低于设定的定位成功判定标准。
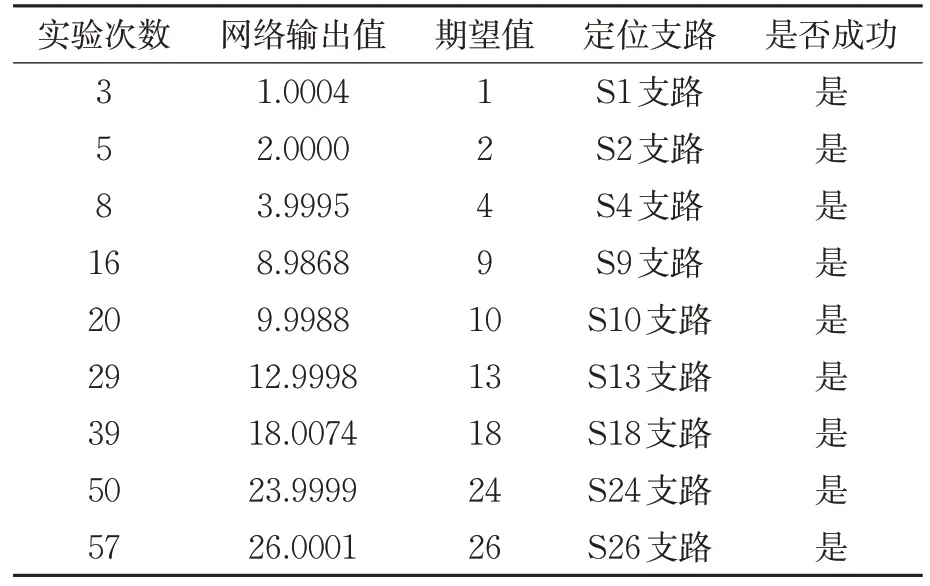
表5 基于RBF神经网络的电网故障定位部分实验结果数据
综上,基于FRFT-RBF神经网络的电网故障定位方法能准确将多用途工程船电网故障定位在具体支路,具有可行性。
4 结论
本文通过对现有船舶电网故障定位方法的分析,针对船舶电网很少配备配网自动化装置的现状,提出了基于FRFT 的故障特征提取方法,并结合采用RBF 神经网络进行故障特征识别训练,形成了一套适合大多数船舶电网现状的基于FRFT-RBF 神经网络的故障定位方法。在船舶电网任意一主汇流排处设置电能检测装置,在电网运行中获取电压或电流故障波形后,通过对故障特征提取和识别,准确定位故障所在的电网支路。通过仿真试验,验证了方法的可行性,为解决船舶电网故障定位提供了新思路。

