点云特征提取精简方法研究

田 赢，陈裕汉，吴学群，刘 洋，韩 啸，张豫宁

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.滇西应用技术大学 地球科学与工程学院，云南 大理 671000）

0 引言

随着三维激光扫描技术的发展，点云数据现已被广泛应用于多个领域，尤其是在物体的三维建模上。但原始点云数据量往往很庞大，且存在较多冗余点，如果直接对原始点云数据进行三维重建，不但不会明显提高精度，而且会加大计算机的运行负担，降低建模效率。因此，在尽可能保留模型特征的同时，对原始点云数据进行精简是很有必要的。

近年来，针对点云精简方法的研究，国内外学者已做了大量工作。现有的传统方法包括：包围盒法［1-2］、均匀/非均匀网格法［3］、随机采样法［4］、曲率采样法［5］、局部熵法［6］、三角网格法［7］、聚类法［8］、概率分布法［9］等。其中，均匀网格法是先找到能包围点云中所有点的立方体，然后将该立方体进一步细分成更小的立方体，并计算每个小立方体的中值点，之后用该中值点替代小立方体内的点。均匀网格法运行速度快，但由于其对点云的特征点和非特征点进行无差别的精简，所以导致精简后的模型容易缺失特征信息。曲率采样法依据在模型的不同位置处点云模型表面曲率的不同对点云进行精简，此方法能够保留一些特征点，但仍存在不足。Song 等［10］提出一种针对点云的全局聚类简化方法，其根据指定的数据约简比，找到原始输入数据集的一个子集，然后通过输入点集与简化点集的最小几何偏差得到全局最优解。但该方法的缺点是时间复杂度高，近似的点—面距离可能会给出不精确的值。Markovic 等［11］利用一种基于ε 不敏感支持向量回归（ε-SVR）的方法识别点云中的特征点，但该方法无法直接简化非结构化点云。Leal 等［12］介绍了一种通过估计点云的局部密度来简化3D 点云的方法，该方法对异常值和噪声具有鲁棒性。付永健等［13］利用点云中的每个点及其近邻点建立拟合曲面对邻域点进行比较，从而完成点云的精简，但该方法对领域点的个数比较敏感。贺一波等［14］根据点云的均方根曲率，利用k-means 聚类算法精简点云，该方法对点云模型特征点保留较好，但对聚类数比较敏感。李佩佩等［15］单纯地运用二分K-means 算法提取大于曲率阈值的点作为最终的精简点，但此算法只适用于表面变化较大的点云模型，对于有较多平坦区域的点云模型则会产生较多空洞。

本文结合了阈值提取和二分K-means 聚类算法来控制特征点提取数量，可以方便地改变精简后特征点与非特征点比例，同时使精简率的控制也变得更加灵活。

1 本文方法介绍

1.1 基于法向量夹角提取整体特征点

点的法向量是重要的几何性质，被许多学者广泛用于寻找折叠点和边界点以及高质量的曲面。在点云模型不同位置处点的法向量与其邻近点法向量之间的夹角是不同的，本文利用这一特性提取点云模型的整体特征点。首先计算点云模型中每个点的法向量。对于法向量的计算，首先对原始点云构建KD-Tree［16］，然后选取点云中的每一点，对其邻近点进行搜索，将包含该点的邻近点拟合成曲面，之后计算领域集的协方差矩阵，求出该矩阵的特征值与对应的特征向量。由主成分分析法可知，最小特征值对应的特征向量即为该拟合曲面的法向量［17］。具体为：假设采样点Pi的邻域集为P={P1，P2，…，Pk}，首先依据式（1）计算领域集的重心。

然后依据式（2）计算领域集的协方差矩阵：

求出该矩阵的特征值λ0、λ1、λ2(λ0≤λ1≤λ2)及其对应的特征向量v0、v1、v2，则最小特征值对应的特征向量v0就是采样点Pi的法向量。之后计算每个点的法向量与其周围领域点法向量之间的夹角，依据一定的阈值提取出整体特征点。依据不同阈值提取的结果如图1 所示，其中绿色点为提取出的整体特征点。

Fig.1 Results of global feature point extraction图1 整体特征点提取结果

1.2 依据曲率利用二分K-means聚类算法提取局部特征点

首先计算出点云的平均曲率，然后依据一定的聚类数k，利用二分K-means 聚类算法对非整体特征点计算出的平均曲率进行聚类。对生成的每个簇计算其平均曲率，以每个簇的平均曲率为分界点提取出大于平均曲率的点作为初步的局部特征点，将余下的点划分到非特征点集。之后计算初步局部特征点的平均曲率，将大于平均曲率的点提取为最终的局部特征点。而对于小于阈值的点，则继续将其划分为非特征点。

1.2.1 点云平均曲率计算

点云中每个点的曲率是表征点云表面变化的一个重要评价指标。一般一个点的曲率越大，表明点所在的表面起伏越大，所以依据曲率可以很好地提取出点云模型中局部变化较大的点。

对于曲率的计算，首先利用KD-Tree 对点云中的每个点进行k领域搜索，然后依据最小二乘法将目标点与领域点进行曲面拟合。设曲面的参数方程为：

则曲面的第一基本公式为：

其中，G、E、F称为该曲面的第一类基本参量。设(u0，v0)为曲面上的任意一点，则其与邻近点的距离可表达为：

用泰勒公式对其展开为：

式（7）为曲面的第二基本公式，其中L、M、N为第二类基本参量。由式（4）、式（7）可得曲面的高斯曲率K和平均曲率H：

主曲率K1、K2与高斯曲率和平均曲率的关系为：

1.2.2 局部特征点提取

二分K-means 聚类算法是对K-means 聚类算法［18］的改进。该算法首先对每个簇进行二类的划分，然后计算划分出的子类误差平方和与父类误差平方和的差值，选择差值最大的那个类为最终待划分的类。最后对该类进行二类的划分，并统计此时的簇数。若没达到目标数则继续进行上述操作，直到达到指定的类数。二分K-means 聚类算法克服了K-means 聚类算法收敛于局部最小的局限，在聚类效果上展现出了很好的稳定性。

本文依据点云的平均曲率，利用二分K-means 聚类算法提取局部特征点，具体流程如下：①依据设定的聚类数对非整体特征点进行聚类；②计算每个类点云数据的平均曲率，对每个类提取出大于平均曲率的点作为初步的局部特征点，将其余的点划分为非特征点；③计算初步局部特征点的平均曲率，将大于平均曲率的点提取为最终的局部特征点，将余下的点继续划分为非特征点。

提取的局部特征点效果如图2 所示，其中红色点为提取出的局部特征点。

Fig.2 Local feature point extraction results图2 局部特征点提取结果

1.3 非特征点下采样

对于非特征点，本文利用改进的体素精简法对其进行下采样，具体流程为：①构建非特征点数据的最小包围盒，并依据设置的最小体素的边长将包围盒不断细分为一个个小的体素；②计算体素内点云的重心与体素内的点到重心的距离，保留离重心最近的点，遍历每个体素，最终保留下来的点即为简化后的非特征点。

将简化后的非特征点与提取出的整体特征点、局部特征点进行融合，即为最终精简的点云。

2 实验结果及分析

本文利用PCL 点云库、Microsoft Visual Studio 2015 开发平台，并使用斯坦福点云数据集Bunny、Gargoyles、Skull对本文方法进行验证。为验证本文所提特征提取方法的有效性，将只利用改进的体素精简法精简的点云与本文方法精简的点云进行对比，然后与传统的随机采样法、曲率采样法和文献［15］中的方法在精简结果、精简后三维重构模型与精简误差3 个方面进行对比。其中，Bunny、Gargoyles、Skull 的原始点云数据量分别为35 947、25 039、20 002。

2.1 特征提取实验分析

本文从整体和局部两方面对特征点进行约束，只采用改进的体素精简法精简的点云与利用本文方法精简的点云对比如图3 所示，其中精简率都约为50%。由图3 可见，只利用改进的体素精简法精简的结果在边角等曲率较大处会出现轮廓缺失，如Bunny 的耳朵轮廓、底部边角处，Gargoyles 的耳朵轮廓、翅膀边缘处，Skull的头顶文字、牙齿等处都出现了不同程度的缺失，而本文精简方法的轮廓却保存相对完整。

Fig.3 Comparison between the improved voxel reduction method and the proposed method图3 改进的体素精简法与本文方法对比

2.2 精简结果分析

Bunny 与传统方法对比的精简结果如图4（a）所示，Gargoyles 与传统方法对比的精简结果如图4（b）所示，Skull与传统方法对比的精简结果如图4（c）所示，精简率都约为50%。如图4 所示，由于随机采样法是对点云数据进行无差别的精简，所以导致Bunny 和Gargoyles 的耳朵轮廓缺失，Skull 的头顶文字模糊不清，并且Bunny 的背部、Gargoyles 的底盘存在大量小的空洞，Skull 的额头部分点云分布也不均匀；曲率采样法由于是提取出曲率较大的点，导致平坦处的点会被大量舍去，所以Bunny、Gargoyles 的耳朵轮廓保存完好，Skull 的头顶文字也较清晰，但是Bunny 的背部、Gargoyles 的底盘和Skull 额头处的点云基本都被舍去；本文方法不仅保证了Bunny、Gargoyles 耳朵轮廓的完整和Skull 头顶文字的清晰，而且使Bunny 的背部、Gargoyles的底盘和Skull额头处的点云也相对均匀。

Fig.4 Reduction results of the proposed method and traditional methods图4 本文方法与传统方法精简结果

Bunny 与文献［15］的方法对比的精简结果如图5（a）所示，Gargoyles 与文献［15］的方法对比的精简结果如图5（b）所示，Skull 与文献［15］对比的精简结果如图5（c）所示，其中Bunny的精简率约为62%，Gargoyles 的精简率约为69%，Skull 的精简率约为64%。由于文献［15］的方法也是提取曲率较大的点，因此Bunny、Gargoyles 数据集的耳朵轮廓，Skull 的头顶文字可以保存得很好，但是Bunny 的背部、Gargoyles 的底盘和Skull 的额头仍有较大空洞。而本文方法在相同的精简率下，不但保证了Bunny、Gargoyles 耳朵轮廓和Skull 头顶文字的清晰，而且使Bunny 的背部、Gargoyles 底盘和Skull额头处的点云也相对均匀。

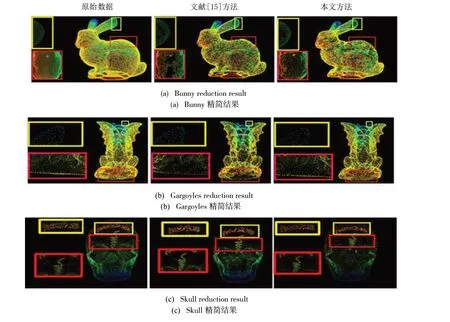
Fig.5 Reduction results of the proposed method and method in literature ［15］图5 本文方法与文献［15］方法精简结果

2.3 三维重建效果对比

在三维重建效果对比方面，本文分别以约30%、50%、70%的精简率与传统方法进行对比，以Bunny 约62%的精简率、Gargoyles 约69%的精简率、Skull 约64%的精简率与文献［15］的方法进行对比。Bunny 与传统方法对比的重构结果如图6 所示，Gargoyles 与传统方法对比的重构结果如图7 所示，Skull 与传统方法对比的重构结果如图8 所示。Bunny 与文献［15］方法对比的重构结果如图9（a）所示，Gargoyles 与文献［15］方法对比的重构结果如图9（b）所示，Skull与文献［15］方法对比的重构结果如图9（c）所示。

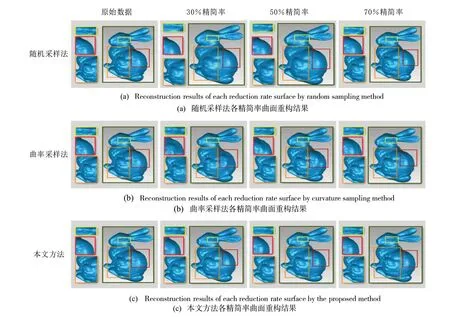
Fig.6 Bunny simplified surface reconstruction results of the traditional method and the proposed method图6 传统方法及本文方法的Bunny精简曲面重构结果

Fig.7 Gargoyles simplified surface re(ccoi)nstruction results of the traditional method and the proposed method图7 传统方法及本文方法的Gargoyles精简曲面重构结果

Fig.8 Skull simplified surface reconstruction results of the traditional method and the proposed method图8 传统方法及本文方法的Skull精简曲面重构结果

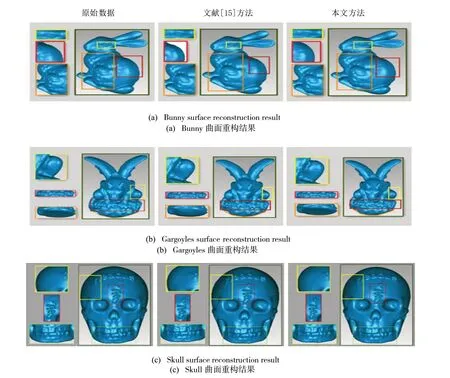
Fig.9 Surface reconstruction results of the proposed method and method in literature ［15］图9 本文方法与文献［15］精简方法曲面重构结果

如图6（a）、图7（a）和图8（a）所示，随机采样法在各精简率下模型特征缺失较严重，Bunny 的眼部、侧面，Gargoyles 的爪子和Skull 的头顶文字、额头标记、牙齿轮廓等细节特征已模糊不清，且精简率越低，该现象越明显。曲率采样法可以很好地保留模型细节特征，但对于平坦区域，则会造成模型严重变形。如图6（b）、图7（b）和图8（b）所示，虽然Bunny 的眼睛、侧面，Gargoyles 的爪子和Skull 的头顶文字、额头标记、牙齿轮廓等处细节特征较为明显，但Bunny 的背部两边翘起，中间低洼，已严重变形，Gargoyles的腿部向里凹陷，底部向外凸起，而Skull 的头顶严重突起，已失去物体原本的面貌，且随着精简率的降低，变形更加严重。而本文方法不仅在Bunny 的眼部、侧面，Gargoyles的爪子和Skull 的头顶文字、额头标记、牙齿轮廓等处的细节特征明显，而且Bunny 的背部相对饱满，Gargoyles 的腿部无明显凹陷，底部相对平坦，Skull 的头颅形状也未发生较大变形。

以下是与文献［15］方法的对比，从图9（a）、图9（b）和图9（c）可以看出，文献［15］的方法和本文方法都可以保证模型细节特征突出，但文献［15］的方法针对较平坦区域仍会发生变形，如Bunny 的背部仍然呈现两边高、中间低的形态，Gargoyles 的底部仍然突起，Skull头颅侧面发生凹陷，而本文方法没有上述问题。

2.4 精简误差对比

本文利用Hausdorff 距离和信息熵来评定点云精简精度，Hausdorff 距离可以描述两个点集之间的相似程度。假设点集A=(a1，a2，…，an)，B=(b1，b2，…，bn)，则可以根据式（13）求得A、B点集之间的Hausdorff距离。

其中，h(A，B)=max min‖a-b‖，a∈A，b∈B。Hausdorff 距离越小，代表两数据集越相近，精简精度越高。信息熵可以定量地评定信息量大小，因此可用其评定精简后点云的特征信息。熵值越大，表示所含的特征信息越丰富。设点集中一点为Pi，邻域点集为P=（p1，p2，…，p）j，则该点的信息熵可以用式（14）表示。

其中，Ei表示点Pi的信息熵，hi、hj表示点Pi、Pj的曲率概率分布，ci、cj表示点Pi、Pj的平均曲率，则整个数据集的信息熵为：

本文方法与传统方法Hausdorff 距离对比的精简结果如表1 所示，本文方法与传统方法信息熵对比的精简结果如表2 所示。其中，Bunny、Gargoyles 和Skull 的精简率都约为50%。从表1 可以看出，曲率采样法精简结果的Hausdorff 距离数值都较高，这是因为曲率采样法只保留曲率较大处的点，而对于较平坦区域的点则会大量舍去，从而造成精简后的点云与原始点云差异较大，因此Hausdorff 距离较大。同时可以看出，不管是Bunny、Gargoyles 还是Skull数据集，本文方法相较于传统方法精简结果，Hausdorff 距离都是最小的。如表2 所示，在3 个数据集上，本文方法的信息熵都是最高的。由此可以看出本文方法相较于传统方法，保留的特征信息最多。

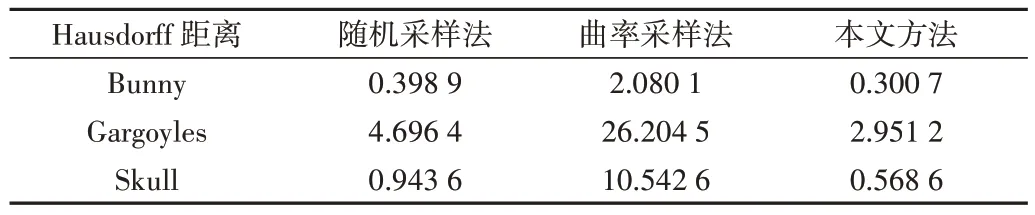
Table 1 Hausdorff distance reduction results of the proposed method and traditional methods表1 本文方法与传统方法Hausdorff 距离精简结果

Table 2 Information entropy reduction results of the proposed method and traditional methods表2 本文方法与传统方法信息熵精简结果

本文方法与文献［15］方法Hausdorff 距离对比的精简结果如表3 所示，本文方法与文献［15］方法信息熵对比的精简结果如表4 所示。其中，Bunny 的精简率约为62%，Gargoyles 的精简率约为69%，Skull 的精简率约为64%。从表3 可以看出，在相同的精简率下，本文方法同样比文献［15］方法精简的Hausdorff 距离要小。从表4 可以看出，在3 个数据集上，本文方法相比于文献［15］的方法，信息熵都是最高的。由此可以看出，本文方法具有较高的精简精度。

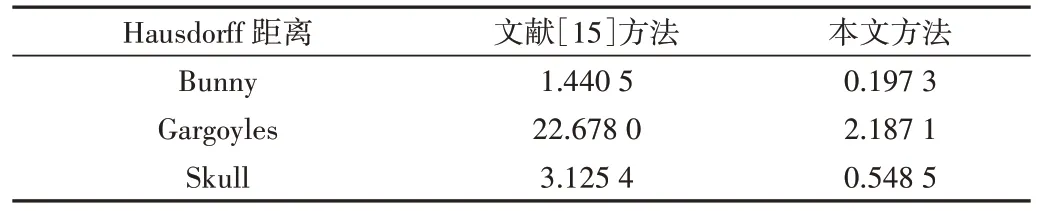
Table 3 Hausdorff distance reduction results of the proposed method and the method in reference ［15］表3 本文方法与文献［15］方法Hausdorff 距离精简结果

Table 4 Information entropy reduction results of the proposed method and the method in reference ［15］表4 本文方法与文献［15］方法信息熵精简结果

3 结语

本文利用法向夹角与基于曲率的二分K-means 聚类算法提取出模型中的特征点，在一定程度上改善了依据单一阈值提取特征点效果较差的问题。对于非特征点则利用改进的体素精简法进行大比例的精简，从而在保证模型完整性的同时，较好地保留了特征点，且重建后的模型细节特征也较为突出。经实验证明，本文算法在保证精简率的同时，也具有较高的精简精度。但是因二分K-means 聚类算法不稳定，不能保证每次都能获得很好的聚类效果，所以导致局部特征点的提取效果也毁誉参半。同时由于本文算法需要计算点云曲率，并对曲率进行聚类划分，因此时间复杂度会比传统的精简方法略高。下一步工作需要对点云特征提取算法的时间复杂度和稳定性方面进行深入研究。