基于Bellman原理的人员密集场所疏散路径优化研究

王 勇，李肖肖，邹成祥，李亚萍

（武汉科技大学 资源与环境工程学院，湖北 武汉 430081）

0 引言

人员密集场所具有人员流动性较强、人员数量和密度大等特点［1］，极易发生拥堵踩踏事故造成人员、财产损失，如“上海12·31 外滩踩踏事故”、“印度10·13 寺庙踩踏事故”［2］。随着我国城市化进程的加快，有多部疏散楼梯、多条穿行通道的建筑和公共场所越来越多，这类建筑或场所的人员疏散过程存在多个决策点，可行性疏散路线较多，合理规划疏散路径可以引导人流，避免或缓解局部拥堵，减少疏散时间，对于提高人员疏散效率、保证生命财产安全具有重要意义［3］。

1 相关研究

目前，国内外学者对人员疏散及其路径优化进行了大量研究。例如，杨乐等［4］针对传统蚁群算法收敛速度慢、搜索时间长、易陷入局部最优等缺点，在其基础上重新定义信息素更新方式，对搜索出的最短路径进行平滑优化处理，使其能快速有效地搜索出最优路径；赵晓东等［5］采用Java 语言设计并实现了给定条件下基于偏好的有向图路径搜索系统，在该系统中，用户可基于偏好输入相关数据得到想要的路径集合，进而从中筛选出最优路径；霍非舟等［6］研究视野受限条件下行人间信息传递对疏散时间的影响，并建立了考虑信息传递的人员疏散元胞自动机模型；谢启苗等［7］建立了一种基于元胞自动机与改进囚徒困境模型的人员疏散仿真模型，并运用该模型考察恐慌心理对人员疏散路径的影响；杜宝江等［8］采用Pyrosim 软件动态模拟火灾情况并输出环境参数，通过改进当量长度代替蚁群优化算法中的几何长度，同时改进目标函数，根据火场环境对信息素挥发系数进行动态更新。仿真实验模拟了火灾发展3个时期的路径优化情况，验证了该算法的有效性和收敛性；袁文涛等［9］在研究一般物流配送路径问题处理方法和数学模型的基础上提出一种改进蚁群算法以提高构建路径的速度和质量，在限量车辆路径问题中采用改进算法优化求解车物流的配送路径；言娟等［10］设计了基于时空拥挤度与建筑信息模型的应急疏散路径优化方法，解决了传统建筑应急疏散路径优化合理度低的问题；张佳瑜等［11］通过实地调查、查阅资料和影像数据，运用地理信息系统对避震疏散空间需求及路径进行优化；万远等［12］通过引入路径寻优方法、改进社会力模型、更新的启发函数和信息素构建了新的行人路径选择与优化机制；Hong等［13］提出基于社会力模型与改进人工蜂群算法的应急疏散路径规划方法；Khalid 等［14］利用动态人群模型与基于免疫的路由机制解决紧急路线规划问题；Nishaben 等［15］提出前向—后向最短路径算法，以图论为基础对多条路径进行组合，以确定精准的应急疏散路径；Min 等［16］提出一种改进量子蚁群算法，采用量子比特表示蚂蚁当前的信息素信息，采用量子旋转门更新信息素信息，该算法可更快找到疏散方案，并且具有较强的鲁棒性；徐橙玮等［17］建立空间多目标优化模型，并采用多目标遗传算法求解出最优疏散路径；Hui 等［18］利用A*算法计算出实际路径，提出针对建筑内部区域的3D 疏散路径模型，规划出最佳路径。

以上研究主要通过建立模型、改进算法或引入最短路径算法规划疏散路径，计算过程较为复杂。目前已有一些疏散模拟软件能快速分析出人员疏散的最佳路径和时间，减少人员伤亡，如STEPS、SGEM、Pathfinder 等，但均存在一定缺陷。例如，Pathfinder 软件内嵌的局部最快算法以总时间最短为目标选择疏散路径，对当前房间不仅考虑运动时间而且考虑由于拥堵造成的排队等候时间，但总时间中忽略了后续房间的排队等候时间，仅以距离与最快速度的比值来预估后续房间的疏散时间［19］，这必将导致该算法不适用于后续房间内存在拥堵的情况。为此，本文以存在多步决策情形的某学生公寓人员疏散为例展开研究，针对Pathfinder 软件模拟结果存在路径利用率不均衡的问题，提出一种基于疏散模拟软件的可代数求解的全局路径优化方法。该方法基于决策点构建可行路径模型，通过综合路径长度、疏散速度和局部最短疏散时间等因素，以总疏散时间最短为目标建立路径优化模型，并基于Bellman 原理进行求解，最终确定最优路径和疏散时间。

2 Pathfinder软件模拟与分析

2.1 学生公寓模拟模型

通过Pathfinder 软件建立的某学生公寓三维模型如图1 所示。该公寓共7 层，1 层有40 间宿舍，2-7 层均有42 间宿舍，每间宿舍容纳4 人。公寓内部的东西两侧各有一部疏散楼梯，楼梯净宽度均为1.8 m；各层房间门净宽度为0.9 m；疏散廊道通行无障碍物，净宽度为1.8 m。公寓共有P1、P2、P33 个安全出口，宽度分别为2 m、2 m、1.2 m。Ma1、Ma2分别为第a+1 层下行到第a 层廊道的西侧、东侧楼梯口。

Fig.1 3-dimensional model of the student apartment图1 学生公寓三维模型图

模型主要参数包括：①人员速度设置。参照文献［20］，将公寓疏散人员的运动速度设定为1.4 m/s；②人员行为与参数设置。人员均采用就近原则选择出口进行疏散，疏散行为模式选用Steering 模式；人员行为设置为自行寻找任意安全出口（Go to Any Exit）；当前门偏好值（Current Door Preference，CDP）及当前房间距离惩罚值（Current Room Distance Penalty，CRDP）均取默认值35。

2.2 模拟结果分析

2.2.1 实时流率与累计人员数量分析

模拟得到的实时流率曲线和累计人员数量分别如图2、图3 所示。由图2 可知，M11的使用时段为6.5-253.5 s，总利用时长为247 s；M12的使用时段为5.5-327.5 s，总利用时长为322 s，M12的 总利用时 长比M11多75 s。由图3 可知，通过M11疏散的总人数为435 人，通过M12疏散的总人数为573 人，通过M12疏散的人数比M11多138 人。在疏散过程中，东、西侧楼梯的使用情况不均衡。

Fig.2 Real-time flow rate curves of M11 and M12图2 M11、M12实时流率曲线

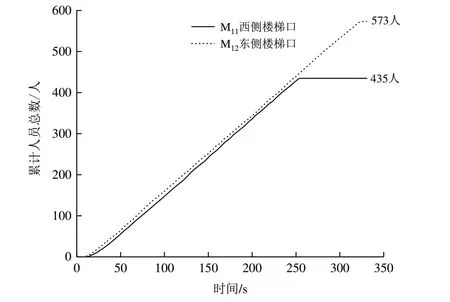
Fig.3 Total number of person passing through M11 and M12图3 通过M11、M12的累计人员数量

2.2.2 模型参数优化分析

由表1 可知，CRDP、CDP 取默认值，总疏散时间为330.3 s。若CRDP=35 m，总疏散时间会随着CDP 参数值的减小而单调减小，CDP 参数取0 为较佳值；若CDP=0，总疏散时间会随着CRDP 参数值的减小而先增大后减小然后再增大，CRDP 参数取35 为较佳值。即使设定CRDP=35 m，CDP=0，经过东西两侧楼梯的人数差值仍为62 人，两侧楼梯的使用情况仍存在较大差异，说明软件本身优化效果不足。

Table 1 Effects of main model parameters on the simulation results表1 主要模型参数对模拟结果的影响

3 学生公寓全局路径优化

在保证疏散路径安全的基础上，本文提出一种以总疏散时间最短为目标的路径优化方法，详细流程见图4。

Fig.4 Path optimization flow图4 路径优化流程

3.1 决策点确定及可行路径模型构建

学生公寓的可行路径模型如图5 所示。第i 层楼的任一房间门Ci及楼梯口Ma1、Ma2构成路径决策点。线段上的数字表示决策点之间的路径长度，各楼层房间门至下一决策点的具体路径长度如表2、表3所示。

Table 2 Path length from C1j to P1，P2 and P3 of the first floor表2 第1层楼房间门Cij至P1、P2及P3的路径长度（m)

Table 3 Path length from Cij to Ma1 and Ma2 of the floor of 2-7表3 第2-7层各房间门Cij至Ma1、Ma2的路径长度（m，i≥2，a=i-1）

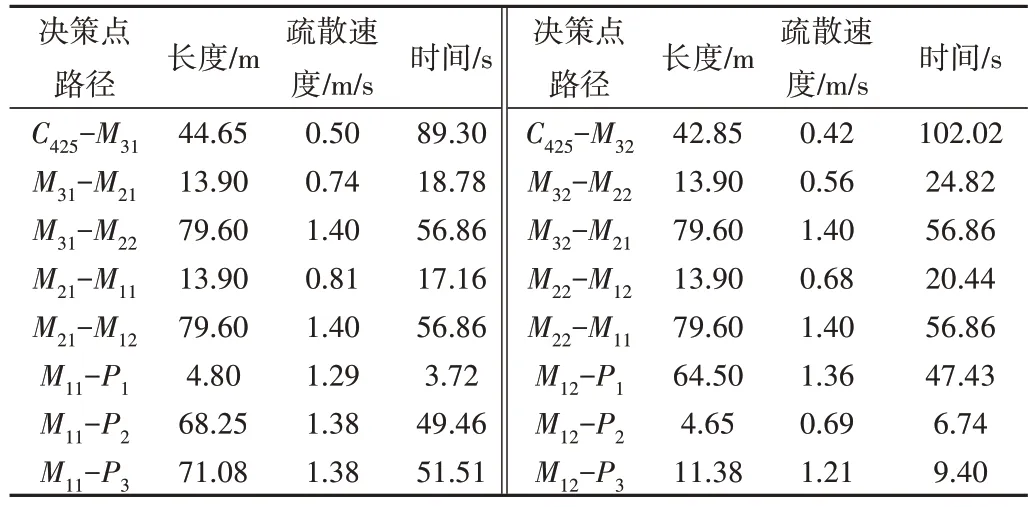
Table 4 Path length，evacuation speed and time of decision nodes between exit and room 425表4 房间门C425至出口各决策点之间的路径长度、疏散速度及时间

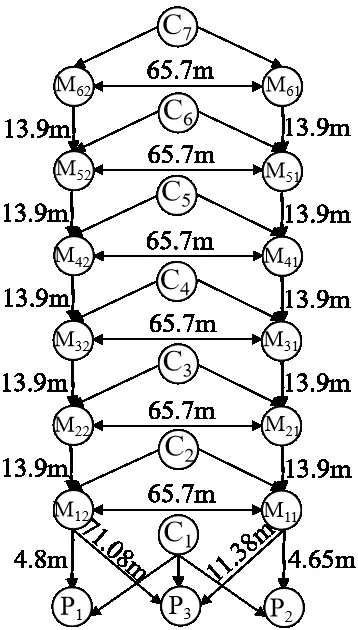
Fig.5 Feasible path model for the student apartment图5 学生公寓可行路径模型

3.2 路径优化模型建立与求解

3.2.1 路径优化模型建立

针对第k阶段的疏散路径优化目标函数为：

式中：k为阶段变量，k=1，2，…，N；gk为阶段指标函数，以疏散时间为阶段指标，其为路径长度和疏散速度的函数，即gk=tk=L/V，其中tk为第k阶段所需疏散时间；L为第k阶段决策点与决策点之间的路径长度，m；V为第k阶段决策点与决策点之间的疏散速度，m/s；Sk为状态变量，用于描述各阶段的状态，包括第k+1阶段的决策；dk～N为第k阶段到第N 阶段的决策。一般情况下，第N阶段的输出状态SN+1已经不再影响本过程的策略，即式中的边界条件fN+1（SN+1）=0。

3.2.2 路径优化模型求解

Bellman 原理为在最优策略的任意一阶段上，无论过去状态和决策如何，对过去决策所形成的当前状态而言，余下的诸决策必须构成最优子策略。基于该原理，可逆序对路径优化目标函数进行求解，即从最后阶段开始逐步向前逆向寻求最短疏散时间。首先求解最后一个阶段的优化目标函数fN（SN），得到该阶段的局部优化决策；然后基于该阶段的决策结果继续求得fN-1（SN-1）所对应的局部优化决策，依此类推，直至求得目标函数f1（S1）所对应的局部优化决策；最后将各局部优化决策整合得到全局优化决策。

3.3 疏散路径优化过程及效果分析

3.3.1 路径优化过程

以公寓第4 层楼25 号（425）房间、第5 层楼23 号（523）房间优化过程为例，其疏散路径优化决策如图6、图7 所示。图中决策点之间各可行路径线段上的数字为疏散时间，其求解所依据的路径长度、疏散速度见4、表5，其中疏散速度来自Pathfinder模拟结果。

Table 5 Path length，evacuation speed and time of decision nodes between exit and room 523表5 房间门C523至出口各决策点之间的路径长度、疏散速度及时间

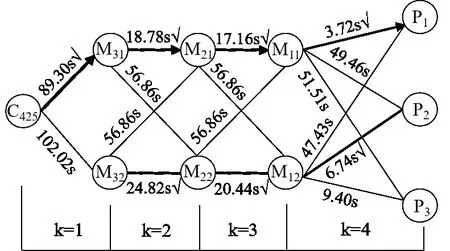
Fig.6 Evacuation path optimization decision for room 425图6 425房间疏散路径优化决策

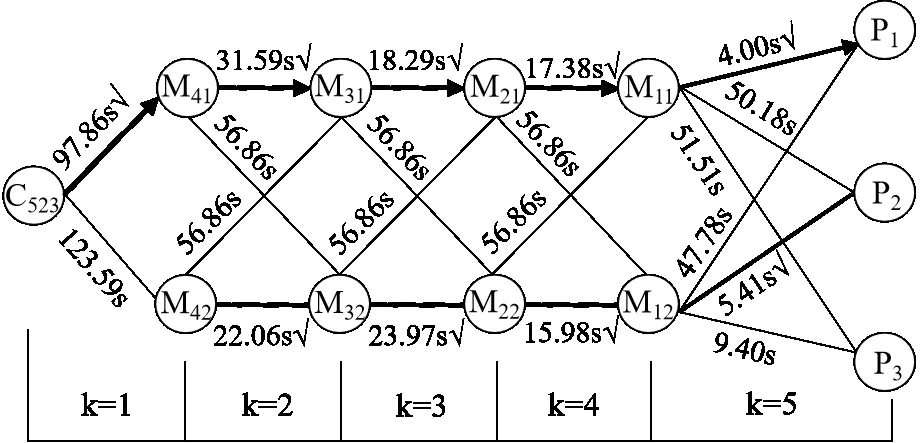
Fig.7 Evacuation path optimization decision for room 523图7 523房间疏散路径优化决策

425 房间的路径决策过程可划分为4 个阶段，即阶段变量k=1、2、3、4。基于Bellman 原理，从最后阶段开始逆序寻求最短疏散时间。首先从阶段k=4 开始，选出该阶段中各决策点之间的最短疏散时间路径，即路径M11-P1；其次，选出阶段k=3 中各决策点之间的最短疏散时间路径，即路径M21-M11；然后选出阶段k=2 中各决策点之间的最短疏散时间路径，即路径M31-M21；最后选出第一阶段k=1 中各决策点之间的最短疏散时间路径，即路径C425-M31。最终得到425 房间的最优疏散路径为C425→M31→M21→M11→P1。同理，523 房间的最优疏散路径为C523→M41→M31→M21→M11→P1。运用优化方法一次运算即得学生公寓所有房间的最优疏散路径（见表6），按该优化路径设置后Pathfinder模拟的公寓人员总疏散时间为292.3 s。

Table 6 Optimal evacuation routes for all rooms表6 所有房间最优疏散路径

3.3.2 优化效果分析

（1）总疏散时间分析。设置优化路径后的模拟结果与原模拟结果相比，公寓的总疏散时间从330.3 s 减少至292.3s。

（2）优化后实时流量与累计人员数量分析。图8 为优化后的实时流量曲线图。可以看出，M11的使用时段为6.5-288.5 s，总利用时长为282 s；M12的使用时段为5-288.5 s，总利用时长为283.5 s。图9 为优化后的累计人员数量图，可以看出，通过M11、M12疏散的总人数均为504人，优化后东、西侧楼梯的利用率相当，公寓整体疏散效率达到最高。

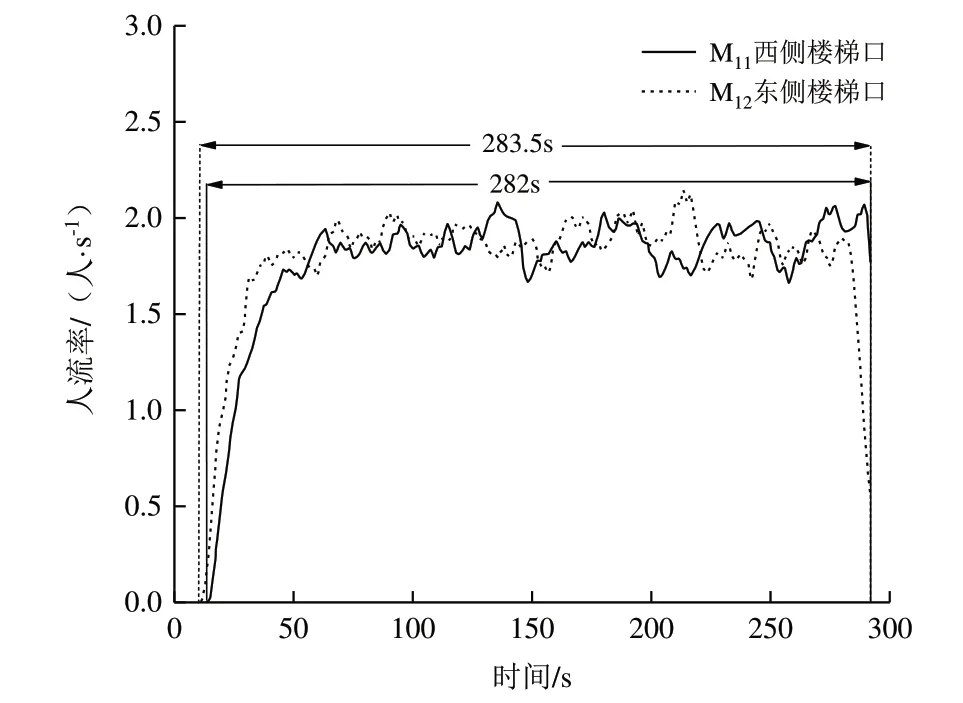
Fig.8 Optimized real-time flow rate curves图8 优化后实时流率曲线

Fig.9 Total number of accumulated person after optimization图9 优化后累计人员数量

4 结语

Pathfinder 软件对学生公寓人员疏散过程的模拟结果表明，东西两侧楼梯的使用情况不均衡，调整模型主要参数为最佳值，即CDP=0、CRDP=35m，此时经过东西两侧楼梯的总人数仍相差62 人，说明软件内嵌的局部最快算法在多决策点密集群体疏散方面存在缺陷，软件本身优化效果不足。为此，本文以总疏散时间最短为目标，在软件模拟结果的基础上确定决策点，以可行路径模型图的方式展现出全局路径，同时通过Bellman 原理简单快捷地代数求解出优化路径，最终得到全局最优疏散方案。路径优化后的模拟结果与原模拟结果相比，总疏散时间缩短了38 s，东侧楼梯处部分人流量被分散至西侧楼梯处，东西两侧楼梯的利用情况达到均衡状态。然而，本文设置的人员疏散情景为紧急疏散，未耦合火灾、地震等具体危险场景。后续研究中可引入火灾情景进行人员疏散，并根据灾害发生地点给不同路径赋予不同的危险度，以区别其可通过程度。通过程序设计，将所提出的全局最优路径优化方法代码化，形成独立于Pathfinder 软件的疏散路径优化工具，或对Pathfinder软件进行二次开发赋予其路径优化功能。