基于概率模型驱动的机载贝叶斯前视超分辨多目标成像方法

陈洪猛 余继周* 张文杰 李亚超 李 军 蔡 良 鲁耀兵*

①(北京无线电测量研究所 北京 100854)

②(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

前视成像雷达(Forward-Looking Radar,FLR)由于在飞行器自主导航，导弹末端制导，自动驾驶等领域具有广阔的应用前景，因此在军事和民用领域越来越受到重视[1–4]。传统的多普勒波束锐化(Doppler Beam Sharpening,DBS)技术[5–7]和合成孔径雷达(Synthetic Aperture Radar,SAR)[8–13]通常采用条带模式或前斜视模式工作。然而，受多普勒成像原理的限制，这两种方法由于多普勒历程的约束无法对飞行方向的正前方区域进行高分辨率成像，从而导致前视盲区。因此，不断追求方位分辨率的提升是前视成像技术不断发展的动力。

为了获得FLR成像场景的细节信息，利用宽带信号和脉冲压缩技术可以获取高距离分辨率。为了克服多普勒历程的约束，最直接的解决思路就是通过引入发射平台和接收平台的空间分集带来的独立多普勒信息进行方位高分辨成像，这也是双基 SAR[14–21]技术可用来提高方位分辨率的关键，但双基前视SAR成像的空间几何关系复杂，特别是空时频同步的精度给收发雷达系统的设计带来较大的复杂度。文献[22–24]充分利用和差通道的信息，将单脉冲测角与前视成像技术相结合提高方位分辨率。杨志伟等人[25]采用实波束重叠扫描的方式，利用波达角(Direction of Arrival,DOA)估计方法和理论实现了前视成像。在 DOA 估计基础上，王军等人[26]和温晓杨等人[27]针对前视成像近似稀疏的场景，通过压缩感知(Compressed Sensing,CS)的方式获取前视成像结果。由于FLR的前视成像方位分辨率主要与天线孔径大小成反比，当天线孔径越来越大时，天线波束宽度将越来越小。在这种情况下，可以获得高方位分辨率，因此近年来实孔径前视成像技术越来越受到关注。研究表明，解卷积技术[28]是一种不改变现有雷达系统体制，利用信号处理手段提高方位分辨率的有效方法。但由于天线方向图的低通特性，直接的解卷积技术是一个病态问题，因此许多改进的解卷积前视成像技术应运而生。李悦丽等人[29]提出一种基于多通道处理的解卷积前视技术，通过利用多个通道信息的联合处理克服解卷积过程中的病态问题，但对于无人机载和弹载雷达系统而言，多通道会增加系统设计的复杂度。为降低系统的复杂度，单通道解卷积技术[30–41]越来越受到国内外学者的关注。文献[31]通过引入l2范数，将正则化方法应用于提高方位分辨率，取得了一定的效果。文献[32–34]将稀疏性约束嵌入到解卷积成像中，进一步提高了前视成像的分辨率，为单通道解卷积技术的发展带来了新的曙光。

为了减轻FLR解卷积前视成像问题的病态性，Huang等人[35]和Tuo等人[36]引入了截断奇异值分解方法(Truncated Singular Value Decomposition Method,TSVD)提高方位角质量。然后，Yang等人将迭代自适应处理(Iterative Adaptive Approach,IAA)方法[37]引入前视成像。正则化方法[38]是将不适定问题转换为附近的条件良好问题的良好工具，该操作可以通过在最小二乘算法上选择不同的正则化约束来实现。正则化可以解决反卷积问题，获得更好的性能。此外，Zhang等人[39,40]提出了基于全变差(Total Variation,TV)的方法来描述场景信息，这在保持目标轮廓方面表现良好。为了充分利用前视成像场景的先验信息，Yang等人提出了基于贝叶斯框架[41–47]的前视方法。

然而，目前的机载前视成像方法的研究主要集中在场景稀疏性先验已知的情况下。真实场景中的稀疏性不能采用单纯的某一种稀疏约束进行表征，特别是当场景中包含多个目标时，此时场景稀疏度的度量和表征是影响复杂场景下前视成像质量的关键。针对此问题，基于先前已经建立的多普勒解卷积前视成像模型[41–44]，提出了一种基于广义高斯概率模型驱动的机载贝叶斯前视超分辨率多目标成像方法。本文的主要贡献是针对多目标场景，自动的迭代选择场景稀疏度参数，并基于贝叶斯准则，将选取的稀疏度表征参数嵌入到前视成像过程中。此外，本文所提出的方法在每次迭代期间都会进行参数更新，从而增加了不同情况，具有鲁棒性。

2 前视成像信号模型

如图1所示，假设机载平台工作在前视成像模式，雷达波束指向与机载平台飞行方向之间的夹角为θ，与水平方向的俯仰角为φ。假设机载平台的飞行速度为v，飞行方向沿X轴正向，飞行高度用H表示。雷达波长为λ，R0为雷达与目标场景中心之间的初始斜距。

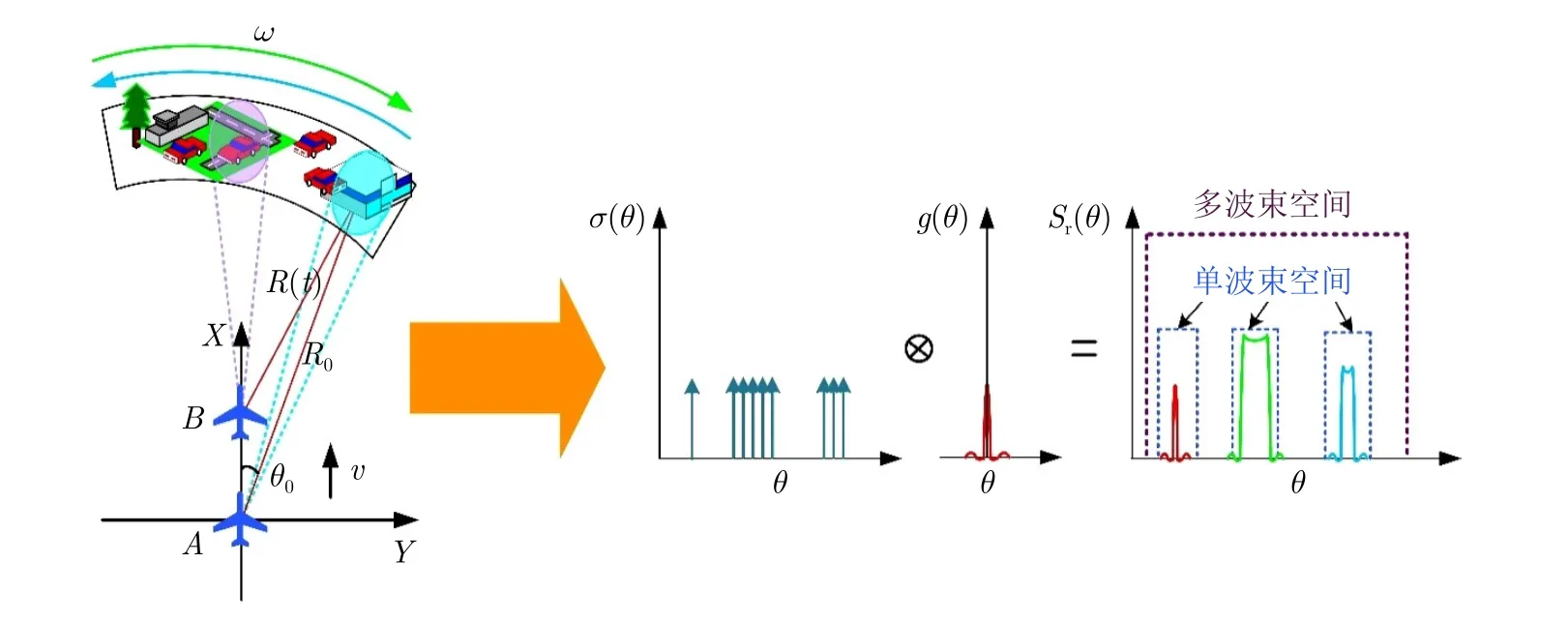
图1 机载前视成像雷达工作示意图Fig.1 Geometry of airborne forward-looking radar

雷达发射线性调频信号：

其中，τ为快时间，fc为发射雷达信号的载频，Tp为脉冲持续时间，rect(τ/Tp)为矩形函数，则回波信号的复包络可以表示为

此时，雷达与场景中任一目标之间的瞬时斜距和瞬时角度值可以表述为

其中，tm为方位慢时间，σ(R,θ)为目标的散射分布函数，fc为雷达载频，Kr为线性调频信号的调频率，h(·) 为天线的方向图，ω为天线的扫描速度。

首先对回波信号进行下变频处理，并进行距离走动校正后的回波信号可以转化为

采用基于Keystone变换的方法对回波信号进行距离走动校正，经过距离走动校正之后，由式(5)可以看出，某一距离单元上的回波信号是天线方向图与目标散射分布函数σ(R,θ)的卷积，即

同时，将回波信号中的噪声用n(θ)表示，则前视成像模式下的回波信号可以简化为

假设方位慢时间维有M个采样点，为了便于分析，将式(7)转化为矩阵形式

其中，σ为目标后向散射系数分布向量，G为天线方向图矩阵，S为方位向雷达接收信号，Φ为多普勒矩阵，n为系统噪声，G和Φ的具体形式如下：

式(9)和式(10)的前视解卷积模型不仅考虑了天线方向图矩阵对散射点的影响，并且考虑了多普勒矩阵的影响。在实际情况下，由于机载平台的运动速度很快，这种影响是不可能消除的。为了提高对前视成像的分辨率，需要对多普勒矩阵进行准确描述，然后再进行后续的前视成像处理。

3 基于广义高斯概率模型驱动的贝叶斯前视超分辨成像方法

3.1 多普勒解卷积前视成像模型

为了降低计算复杂度，在保证前视成像质量的前提下，参考以前的工作[37,44–46]，对式(8)进行化简，根据目标的斜距历程，可以求得目标的多普中心频率为

将θ(tm)=θ0-ωtm代入式(11)，并进行泰勒展开，则瞬时多普勒可以修正为

由于机载雷达主要工作在前视状态，|θm|≤10°。为了后续的工程应用和实现，式(12)可以简化为

此时1阶多普勒解卷积模型下的前视回波信号可以简化为

经过化简之后，由于多普勒运动所引起的相位因子可以描述为

为提高多普勒解卷积的性能，提取先验信息是重要的。更通常的做法是将稀疏信息用于前视雷达成像中。然而，在单波束空间中散射源并不是完全满足稀疏性的假设。

为解决这一问题，利用多波束空间下的解卷积前视成像模型[44]。在方位上将单波束回波交联形成高维空间。即使呈现局部聚集特性的多个散射点在单帧数据内不满足稀疏性假设，在多帧数据组成的联合高维空间内仍可以看作是稀疏的。此时前视成像场景的稀疏性得到改善，高维空间下的回波信号可表示为

在一个距离门内，式(16)可以进一步表示为

其中，Y和X分别是高维空间回波矩阵和散射矩阵。P为波束数量，H和Φ为天线矩阵和扩展的多普勒卷积矩阵，表达式为

3.2 基于广义高斯概率模型驱动的贝叶斯前视超分辨成像

为了获取高分辨的前视成像结果，需要对式(17)进行多普勒解卷积求解。国内外的学者通过将稀疏性约束嵌入到解卷积成像中，在一定程度上改善了前视成像的方位分辨率。但是，由于前视成像场景的复杂性，单纯的某一种稀疏约束无法完整地刻画真实的场景。

为了更加准确地描述前视成像场景的稀疏度，本文采用广义高斯概率模型对前视成像场景中的散射点分布特性进行统计建模，其表达式可以描述为

在多波束空间中，本文采用一组仿真数据对成像场景的稀疏特性进行直方图统计，并分别采用高斯模型、Laplace分布和广义高斯模型进行拟合。图2给出了某一距离单元回波信号的直方图统计，场景参数如表1所示。从图2可以看出，当场景复杂时，传统的Laplace分布的稀疏性假设[30,41,46]已经不能完整地刻画复杂场景的稀疏度，场景稀疏度的失配在一定程度上会导致成像质量的下降。因此，场景稀疏度的度量和表征是影响前视成像质量的关键。

表1 点目标仿真实验雷达参数Tab.1 Radar parameters for simulation experiment with point targets

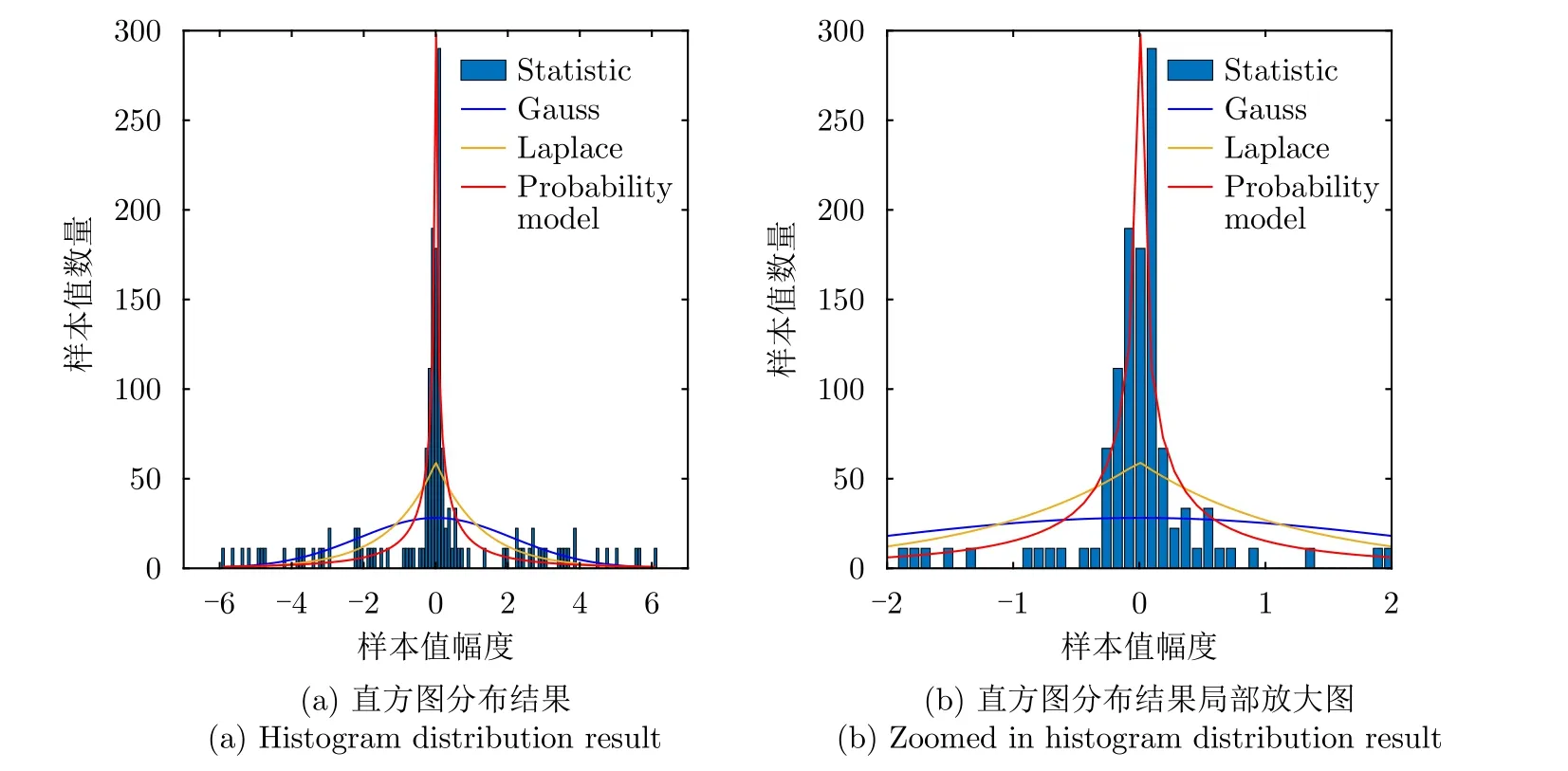
图2 某一距离单元的直方图分布统计Fig.2 Histogram distribution for one range cell

在满足独立同分布(i.i.d.)的假设条件下，成像场景的稀疏度可以采用概率密度函数进行描述，具体表达式为

经化简，前视成像问题可表示为

其中，µ=2ε2b是归一化参数，用于平衡稀疏性与前视成像质量，它与回波信号、噪声水平、形状系数等多个因素有关，本文主要采用最小二乘方法设定，详细的参数选取方法见文献[48]。

对式(24)进行进一步的化简，可得到

为获得前视稀疏成像的最优解，对X求J()的梯度，得到

此时，式(26)可以通过准牛顿方法获得迭代解，表达式为

其中，n为迭代次数，A=2(H ⊙Φ)HH ⊙Φ+µΛ，通过不断迭代求解，直至满足终止条件，最终得到图像矩阵+1。假设M表示单个波束空间的方位采样点数，P表示多波束空间中的单波束个数，N代表迭代计算的次数，则本文方法的计算复杂度约为O(N(PM)3+N(PM)2)。具体的算法处理步骤如算法1所示。

4 仿真和实测实验结果分析

本节将进行仿真和实测数据验证所提方法的有效性，试验结果将实际波束方法、TSVD方法、Tikhonov方法、IAA方法、贝叶斯方法和本文所提出的方法进行了比较。后文将提出的方法简写为PM-Bayesian (Probability Model-driven airborne Bayesian)。

4.1 点阵目标仿真实验结果

图3给出了真实的原始场景，成像场景由14个点目标组成，机载雷达的部分参数如表2所示，仿真过程中回波的信噪比(Signal-to-Noise-Ratio,SNR)设置为10 dB，其中SNR定义为

算法 1 前视超分辨成像方法求解流程Alg.1 Solution flow of the proposed algorithm

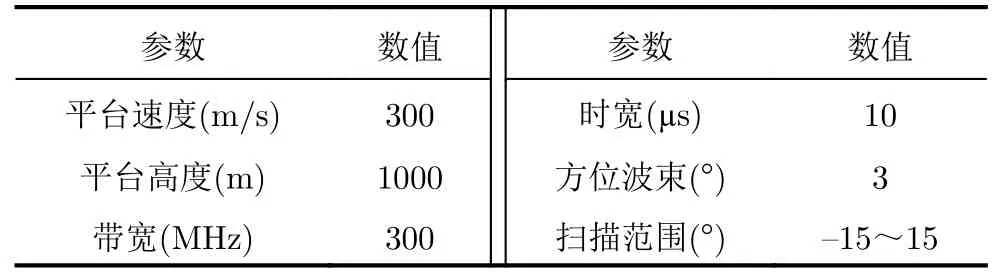
表2 面目标仿真实验雷达参数Tab.2 Radar parameters for simulation experiment with surface targets

图3 真实的点目标分布场景Fig.3 True point targets distribution scene

其中，Ps和Pn分别表示回波与噪声的平均功率。

从图4可以看出，由于真实场景中最邻近点目标之间的角度间隔小于天线的波束宽度，所以实波束方法存在明显的信号混叠现象，且受限于天线方向图的调制作用，无法对点阵目标进行较好的前视成像。TSVD方法由于受到噪声的严重影响，成像结果存在模糊，这可能是由于在低信噪比下难以选择合适的奇异值所导致的。Tikhonov方法保持了前视成像结果的完整性，但在目标周围出现了一些副瓣。IAA方法的成像结果目标轮廓清晰，信息保持完整。但对于相邻的非常近的两个目标无法很好的区分。图4(e)和图4(f)显示了贝叶斯和提出的PM-Bayesian方法的成像结果。这两种方法都可以获得高分辨的前视成像结果，并且所提出的PMBayesian不仅提高了前视成像分辨率，而且周边的副瓣和噪声更低，从而在一定程度上抑制了噪声。图4(g)给出了不同方法在某一距离单元的前视成像结果对比图，从中可以看出所提出的PM-Bayesian不仅可以准确地对前视场景中的散射点进行成像，还可以获得较低的副瓣，从而为后续的目标识别提供支撑。

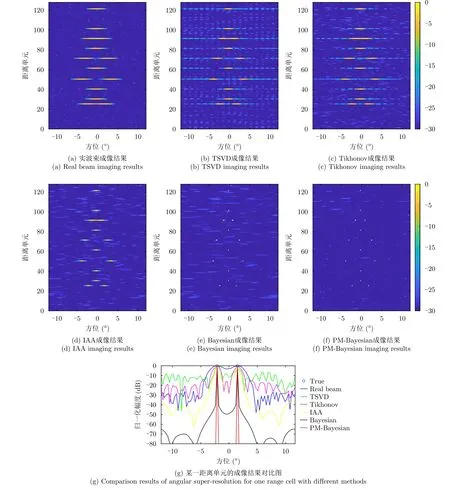
图4 不同方法的前视成像结果对比Fig.4 Angular super-resolution results of different methods

为了定量评估不同前视成像算法的性能，进行了100次蒙特卡罗实验，统计出不同方法在不同SNR下的均方根误差(Root Mean Square Error,RMSE)变化曲线。其中RMSE定义为

从图5可以看出，随着SNR的提升，每一种前视成像方法的RMSE都会降低，并且当SNR降低时，所提出的PM-Bayesian的RMSE变化相对较小，试验结果表明本文方法具有较强的稳健性。

图5 不同SNR下的仿真点目标RMSE变化曲线Fig.5 RMSE curves of simulation point targets under different SNRs

4.2 复杂面目标仿真实验结果

为了进一步验证所提出方法的性能，本节将考虑更复杂的飞机模型，并且场景中包含了3架飞机模型，如图6所示，仿真过程中回波的SNR设置为20 dB。

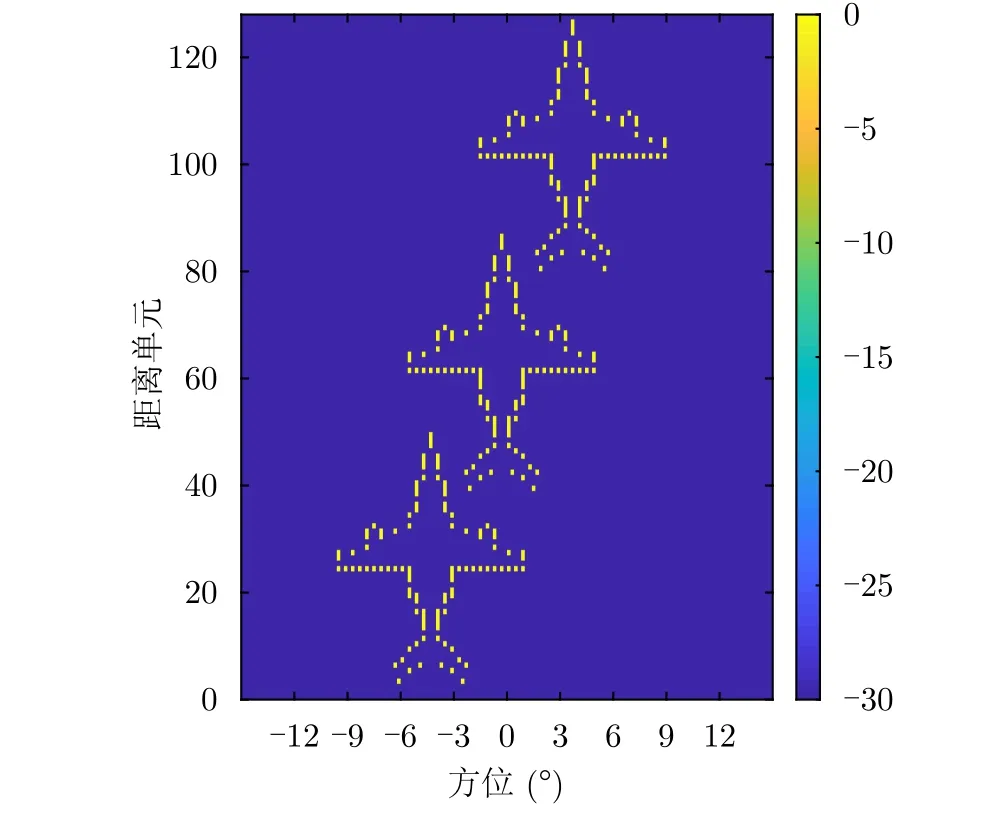
图6 真实成像场景Fig.6 True original scene of surface targets

图7给出了采用不同前视成像方法进行前视成像的结果，从中可以看出实波束方法出现了模糊，无法进行高分辨前视成像。图7(b)—图7(d)分别是TSVD,Tikhonov和IAA方法处理的结果，从中可以看出虽然方位分辨率得到了改善，但是在不同的距离门还存在许多虚假点目标，背景噪声的基底很大，不利于后续的目标检测。图7(e)—图7(f)是贝叶斯和PM-Bayesian的处理结果，从中可以看出，虽然贝叶斯方法可以获得目标的轮廓信息，但本文提出的PM-Bayesian成像结果可以获得更多的细节信息，不仅方位副瓣很低，而且背景噪声很干净，对后续的目标识别提供了高清的成像结果。

图7 不同方法的多目标前视成像结果对比Fig.7 Angular super-resolution results of different methods for multitarget scenario

针对复杂面目标的场景，图8给出了不同前视成像算法在不同SNR下的RMSE变化曲线。从图8可以看出，在SNR较高时，每一种前视成像方法的RMSE都会降低，但在低SNR条件下，本文所提出的PM-Bayesian的RMSE更小。上述原因主要是由于PM-Bayesian选取的稀疏度表征参数嵌入到前视成像的整个过程中，在每次迭代期间都会进行前视成像参数的更新，从而确保了本文方法在低SNR条件下仍具有较强的稳健性。

图8 不同SNR下的仿真面目标RMSE变化曲线Fig.8 RMSE curves of simulation surface targets under different SNRs

4.3 实测数据实验结果

为了进一步验证本文方法的有效性，本文采用一组北京无线电测量研究所在2019年录取的实测数据进行分析，本组实验数据场景中包含了房屋建筑物、道路等典型目标，不同方法下的成像结果如图9所示。

图9 不同方法的实测数据前视成像结果对比Fig.9 Angular super-resolution results of different methods for real data

从图9可以看出，实波束成像方法的方位向模糊严重，无法在方位维度对目标进行很好的分辨。图9(b)和图9(c)分别是TSVD和Tikhonov方法的成像结果，从中可以看出，方位分辨率虽然有了提升，但成像质量依旧较差。图9(d)和图9(e)分别是IAA和贝叶斯方法的成像结果，从中可以看出建筑物和道路信息已经开始清晰。本文提出的PMBayesian成像方法如图9(f)所示，从图9(f)可以看出，图中的建筑物房屋得到了很好的区分，详细的细节信息如图10中红色矩形框中所示。

图10 不同方法的前视成像结果局部放大对比图Fig.10 Zoomed in results of different methods

图10(a)中，基于真实波束的前视成像结果模糊，这意味着方位分辨率较差。如图10(b)和图10(c)所示，基于TSVD和Tikhonov方法的成像结果优于实波束方法。特别在图10(d)的IAA方法已经可以对图中的2个建筑物进行很好区分，然而，图像中仍然存在一些阴影和旁瓣。图10(e)中，我们可以看出贝叶斯方法可以实现比IAA更好的分辨率，并且可以获取目标的轮廓信息。相比之下，所提出的PM-Bayesian算法不仅可以恢复更详细的建筑物信息，而且成像结果中的噪声和副瓣更小。因此，所提出的PM-Bayesian方法的结果具有更高的方位超分辨率能力和更好的噪声抑制能力。基于实测数据的处理结果表明，本文提出的前视成像方法无论在视觉效果还是在成像质量都优于其他方法，从而验证了本文方法的有效性。

5 结语

解卷积方法可以进行前视成像，但当前视成像场景复杂时，现有的前视成像方法的成像质量会下降。本文主要针对机载高速平台的前视成像问题进行了分析，提出了一种基于概率模型驱动的机载贝叶斯前视超分辨多目标成像方法。通过将前视成像空间扩展到多帧数据空间提升场景的稀疏度，并采用广义高斯概率模型对成像场景的稀疏特性进行统计建模和表征，最后基于贝叶斯框架实现稀疏前视成像。仿真结果和实测数据表明，由于选取的稀疏度表征参数嵌入到前视成像的整个过程中，在每次迭代期间都会进行前视成像参数的更新，因此本文方法不仅可以获得高分辨成像结果，而且具有较强的鲁棒性。

本文主要针对弱稀疏场景下的多目标前视成像问题进行了研究，后续将继续挖掘更多的场景先验信息，研究更加稳健的成像网络模型，提升复杂非稀疏场景下的单通道前视成像性能。

利益冲突所有作者均声明不存在利益冲突

Conflict of Interests The authors declare that there is no conflict of interests