七轴机械臂避奇异轨迹规划
周嘉文,刘相权,张晓磊,白宇珅
(1.北京信息科技大学 机电工程学院,北京 100192;2.北京思灵机器人科技有限责任公司,北京 100192)
0 引言
目前,七轴机械臂已广泛应用到各行各业中,具有成本低、精度高,以及能够替代危险工作等优势。机械臂在提高人们生活质量和解放生产力方面有着巨大作用[1]。机械臂在进行运动前要进行轨迹规划,奇异问题的解决是机械臂轨迹规划的前提[2]。当机械臂处在奇异位置时,可能有无数个运动学逆解[3]、自由度缺失[4],甚至关节加速度无穷大[5],速度跳变会产生巨大冲击[6],对机械臂产生不可控的危害,使机械臂无法按照期望轨迹运动。避奇异的同时保证关节角度不超过关节极限,从而使机械臂能够以良好的速度和姿态进行轨迹运动,具有重要的工程意义。
赵龙泽等[7]提出了一种微分项提取和二次拟合的奇异回避算法,但是未考虑到关节角的极限。金荣玉等[8]针对空间机械臂的动力学奇异进行了研究。段锐等[9]针对机器人拖动示教中的奇异问题提出了导纳控制框架进行避奇异,但是在大阻尼情况下这种方法会造成机械臂灵活性降低。Zhao等[10]通过将机械臂引入到粒子群算法中,得到末端实际位姿。Wong等[11]利用了神经网络算法进行运动规划,但神经网络方法的计算成本太高。Teshigawara等[12]则对产生奇异的机械结构提出了解决方法,但是并不适用于高自由度机械臂。
本文应用阻尼最小二乘法避奇异,并采用零空间下的自运动限制关节角到达关节极限,并提出一种新的自运动计算方法来计算自运动的关节速度。以思灵七轴机械臂为例,对上述方法进行了详细的说明,最后进行了仿真和实验验证。
1 机械臂运动学分析
1.1 运动学建模
以思灵机器人公司的七轴Diana7机械臂为研究对象,机械臂模型如图1所示,各关节均为旋转关节。机械臂的改进D-H(modified Denavit-Hartenberg)参数见表1。机械臂的改进D-H坐标系如图2所示。
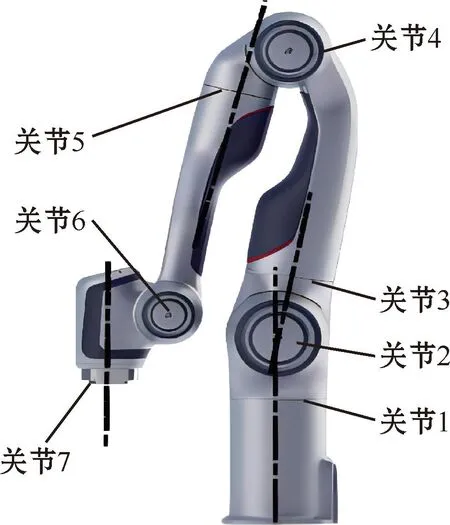
图1 机械臂模型Fig.1 Manipulator model
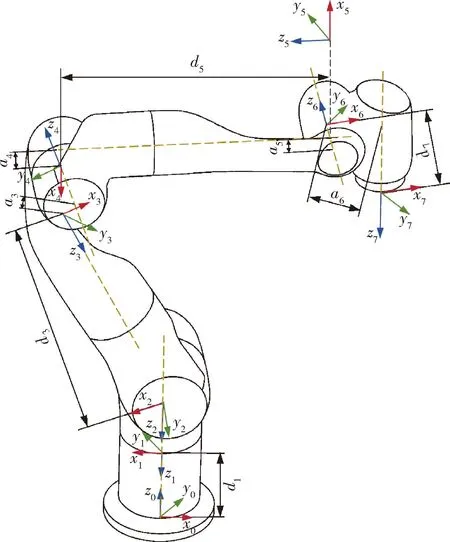
图2 机械臂D-H坐标系示意图Fig.2 Schematic diagram of the manipulator D-H coordinate system
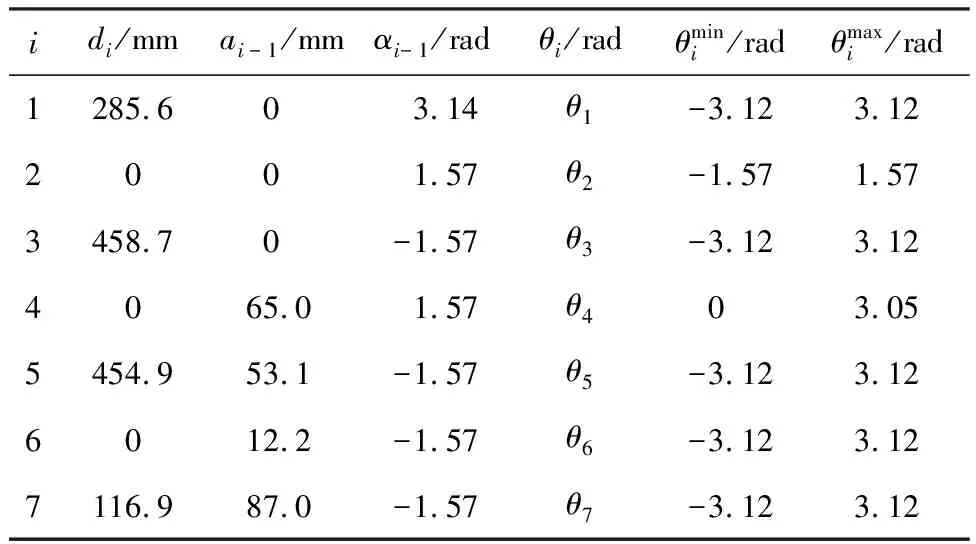
表1 改进D-H参数Table 1 Modified D-H parameters
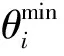
在笛卡尔空间中,根据机械臂的正运动学可以得到:
x(t)=f(θ(t))
(1)
式中:x(t)为t时刻下机械臂末端在空间中的位姿,包含位置和角度两部分;θ(t)为机械臂在t时刻下各个关节的角度。
(2)
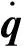
(3)
机械臂的雅可比矩阵J的维度为6×n,其中行数6对应空间中3个平移和3个旋转的自由度数量和,而列数n与机械臂的n个关节数量相对应。六轴机械臂有6个关节,所以雅可比矩阵为6×6的构型,雅可比矩阵为方阵,可以通过式(3)直接求得机械臂的关节速度。然而对于有7个关节的七轴机械臂,雅可比矩阵J为6×7的构型,不能直接应用矩阵求逆操作来计算其逆矩阵。所以我们需要求取J的伪逆矩阵来进行雅可比矩阵的求逆计算。
首先根据表1的参数建立转换矩阵:
(4)
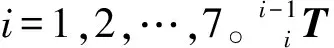
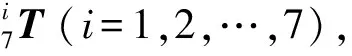
(5)
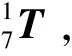
(6)
然后令式(6)每列前三行组成一个列向量:
a1=[a1x,a1y,a1z]T
(7)
b1=[b1x,b1y,b1z]T
(8)
c1=[c1x,c1y,c1z]T
(9)
d1=[d1x,d1y,d1z]T
(10)
最终得到雅可比矩阵第1列:
J1=[(d1×a1)z(d1×b1)z(d1×c1)za1zb1zc1z]T
(11)
式中:(d1×a1)z代表d1和向量a1叉乘后得到的向量中取z分量,(d1×b1)z和(d1×c1)z同理。
按照式(6)到式(11)的这种方法依次得到J2、J3、J4、J5、J6和J7,将它们按照顺序把7组列向量组合到一起组成雅可比矩阵:
(12)
最后采用文献[14]所使用的奇异值分解(singular value decomposition,SVD)方法求取雅可比矩阵的伪逆。SVD奇异值分解方法可以使矩阵J被分解为3个特殊矩阵的乘积,即J=UΛVT。其中,U和V均为正交矩阵;Λ为奇异值组成的对角矩阵。通过这样的分解,可以得到雅可比矩阵J的伪逆矩阵J+:
J+=(UΛVT)-1=(VT)-1Λ-1U-1=VΛ-1UT
(13)
通过将式(3)中的普通逆矩阵J-1替换为伪逆矩阵J+,得到七轴机械臂通过伪逆方法求得的关节速度为
(14)
1.2 阻尼最小二乘法
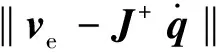
(15)
J*=(J+)T(J+(J+)T+λ2I)-1
(16)
式中:I为单位矩阵;λ为阻尼系数,规定其具体取值和奇异值的大小有关:
(17)
式中:λmax为设置的最大阻尼系数;σ为最小奇异值;σ0为设置的阈值。
通过将式(14)中的伪逆矩阵J+替换为式(16)的奇异鲁棒性逆矩阵J*,最终得到使用最小二乘法进行求解关节速度的表达式:
(18)
1.3 零空间自运动
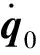
(19)
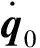
因为不是所有的关节速度向量都在零空间内,所以假设I-J+J为机械臂的零空间投影矩阵。雅可比的伪逆J+和原矩阵J相乘结果是一个单位矩阵I,即J+J=I,把关节速度转换到零空间得到:
(20)
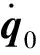
(21)
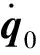
(22)
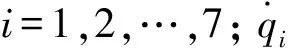
(23)
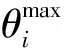
机械臂关节1的关节范围为-3.12~3.12 rad,假设最大关节速度为1.5 rad/s,依据式(22)通过在不同阶段设置不同的k值,得到的关节1关节速度q1大小对应不同关节角度如图3所示。
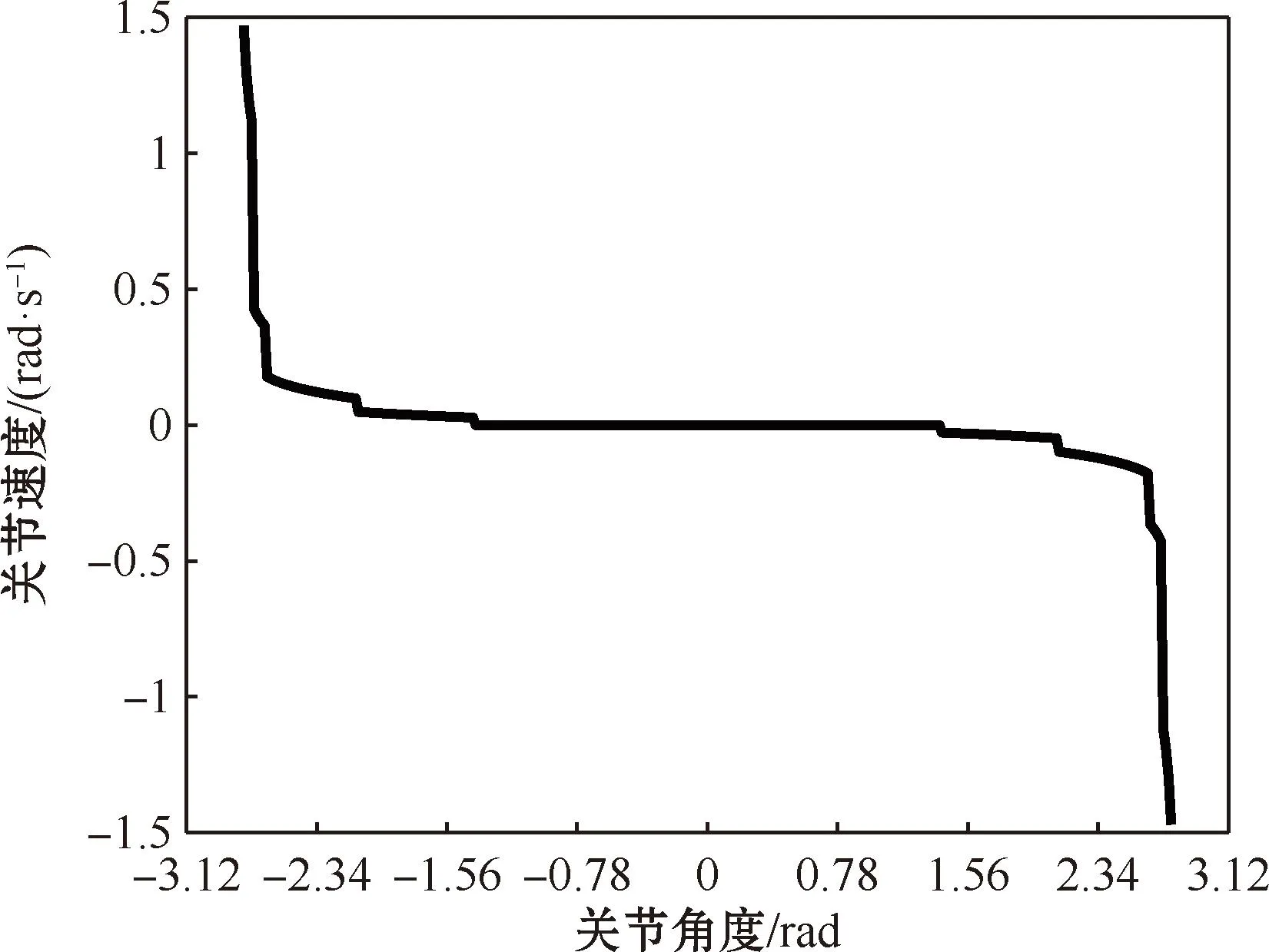
图3 关节1关节角度和速度关系Fig.3 Relationship between joint angle and speed of joint 1
可见,在远离关节极限位置时,关节速度为0;当关节转至接近最小关节极限时,关节改变速度方向以大于0的速度运动,使关节角度远离最小极限位置;当关节转至接近最大关节极限时,关节改变速度方向以小于0的速度运动,使关节角度远离最大关节极限,可以实现防止关节到达关节极限的目的。
(24)
最终结合式(18)、式(21)和式(24)得到应用阻尼最小二乘法和零空间自运动进行求解的关节速度为
(25)
2 运动学算法实现流程
机械臂的可操作度(manipulability measure)是评估机械臂在给定姿态下的运动能力的一个指标。依据文献[18],在机械臂运动过程中,可以通过判断机械臂的可操作度值的大小进行奇异判断。机械臂的可操作度表达式为
(26)
O(θ)值越大,说明机械臂在当前姿态下的运动能力越强。当可操作度为0时,判断机械臂当前时刻的位姿处于奇异状态。为了提前预判奇异状态,需要定义一个阈值常量ε(ε>0)。当机械臂可操作度大于ε时,判断当前机械臂远离奇异状态;当可操作度小于等于ε,机械臂接近奇异状态。算法具体步骤如下:
1) 根据任务目标确定机械臂的初始位置和终止位置。
2) 启动机械臂,通过当前时刻的关节角度数据进行雅可比矩阵的求解,并设置可操作度阈值。
3) 通过式(26)计算运动过程中每个点的可操作度并进行奇异判断,如果当前姿态的可操作度O(θ)大于阈值ε,则不处在奇异位置,机械臂采取式(14)中能够保持运动精度的伪逆法计算关节速度并进行运动,否则,机械臂将会采取式(25)中阻尼最小二乘法和零空间自运动的计算方法进行移动。
4) 实时判断运动过程中每个位置的机械臂是否奇异,并持续控制机械臂进行运动,直到机械臂运动到任务目标位置。
上述整个算法的流程如图4所示。
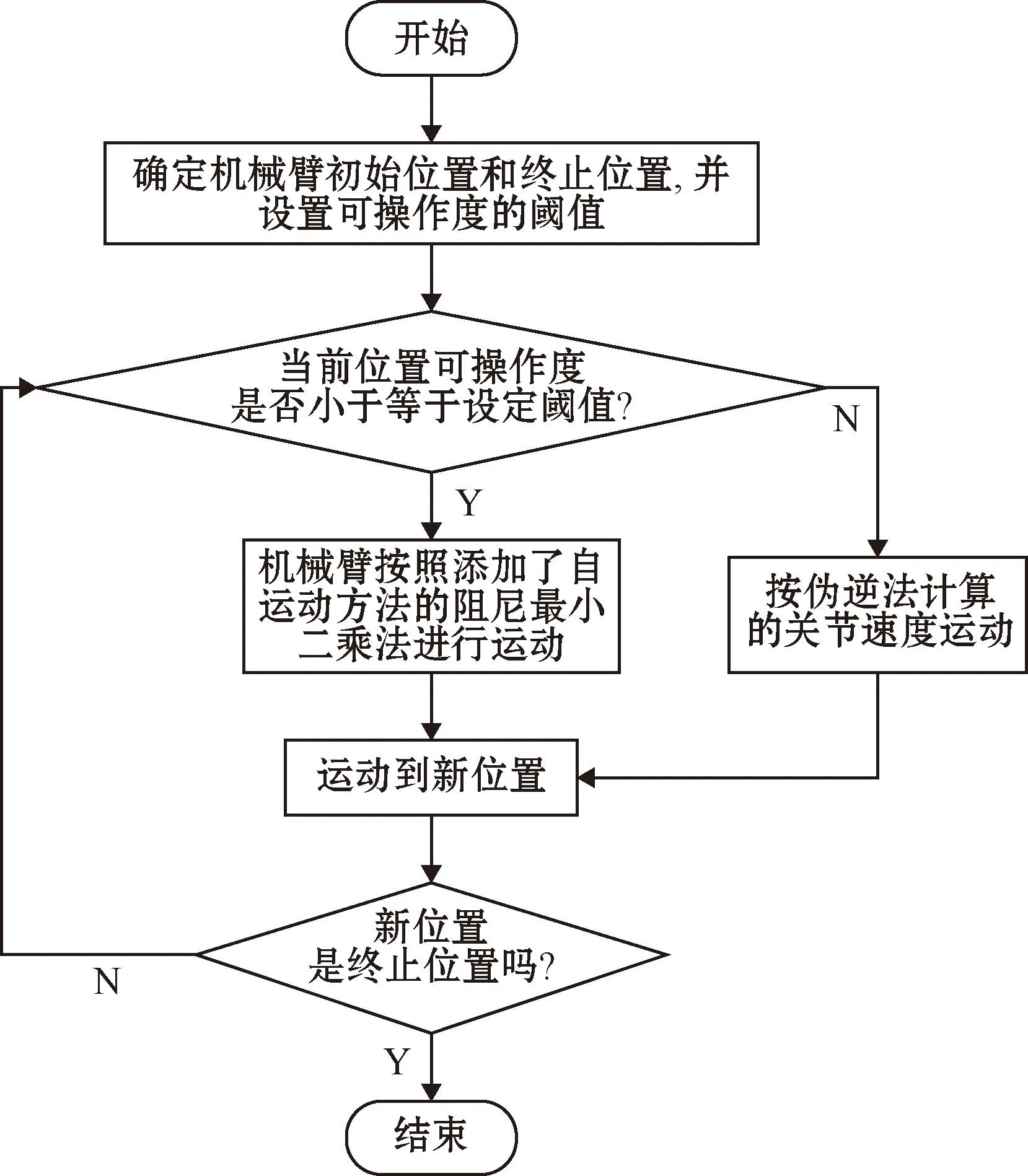
图4 运动学算法实现流程Fig.4 Implementation process of kinematic algorithm
3 仿真及实验
3.1 机械臂可操作度
在机械臂关节范围下,不同的关节角度能够使末端在空间中达到不同的点,每个点对应的可操作度Oi(θ)可以根据式(26)求出。通过比较每个点的可操作度大小,可以识别出最大的可操作度Omax(θ)。随后,每个点的可操作度Oi(θ)与Omax(θ)相除,从而将原始的可操作度归一化到0~1的范围,相应的仿真结果如图5~8所示。图中不同颜色代表着可操作度的不同,其中红色代表可操作度最好,蓝色代表可操作度最差,由图7和图8明显可见在最外层和最内层为蓝色,代表着机械臂在最大关节极限和最小关节极限位置的可操作度较差,蓝色区域范围大,所以避开极限位置非常重要。
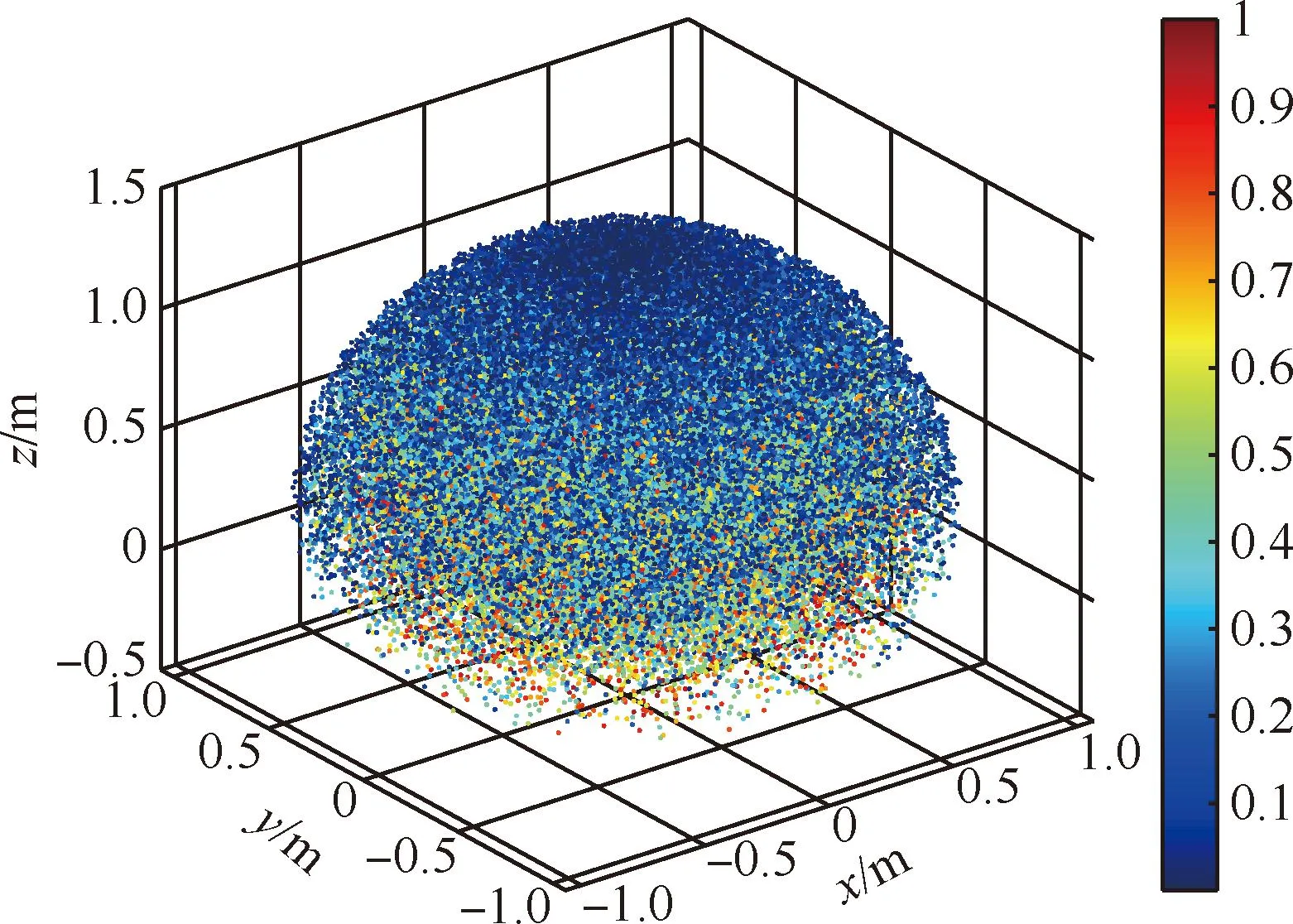
图5 机械臂可操作度点云图Fig.5 Manipulability measure point cloud of manipulator

图6 X-O-Y平面可操作度点云图Fig.6 Manipulability measure point cloud of X-O-Y plane
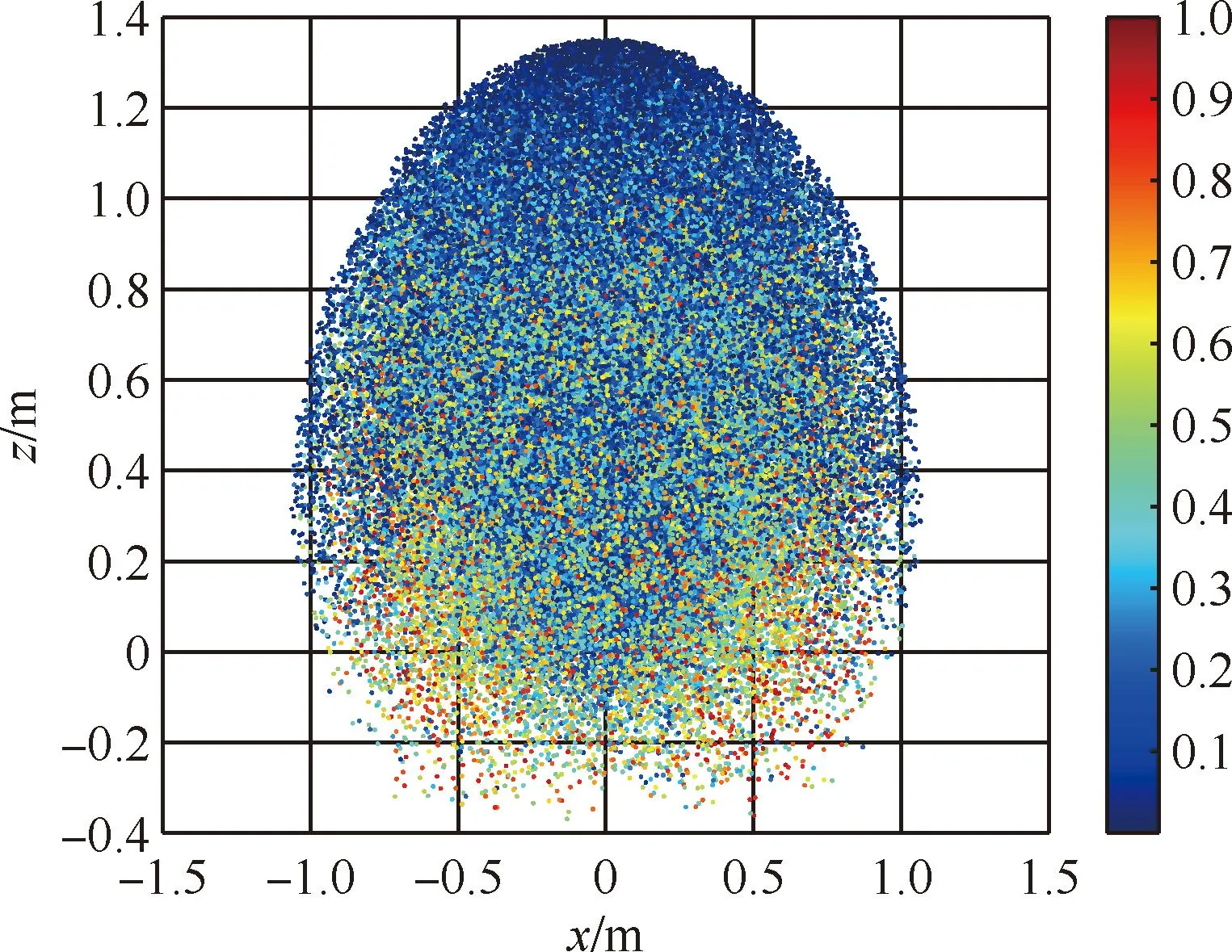
图7 X-O-Z平面可操作度点云图Fig.7 Manipulability measure point cloud of X-O-Z plane
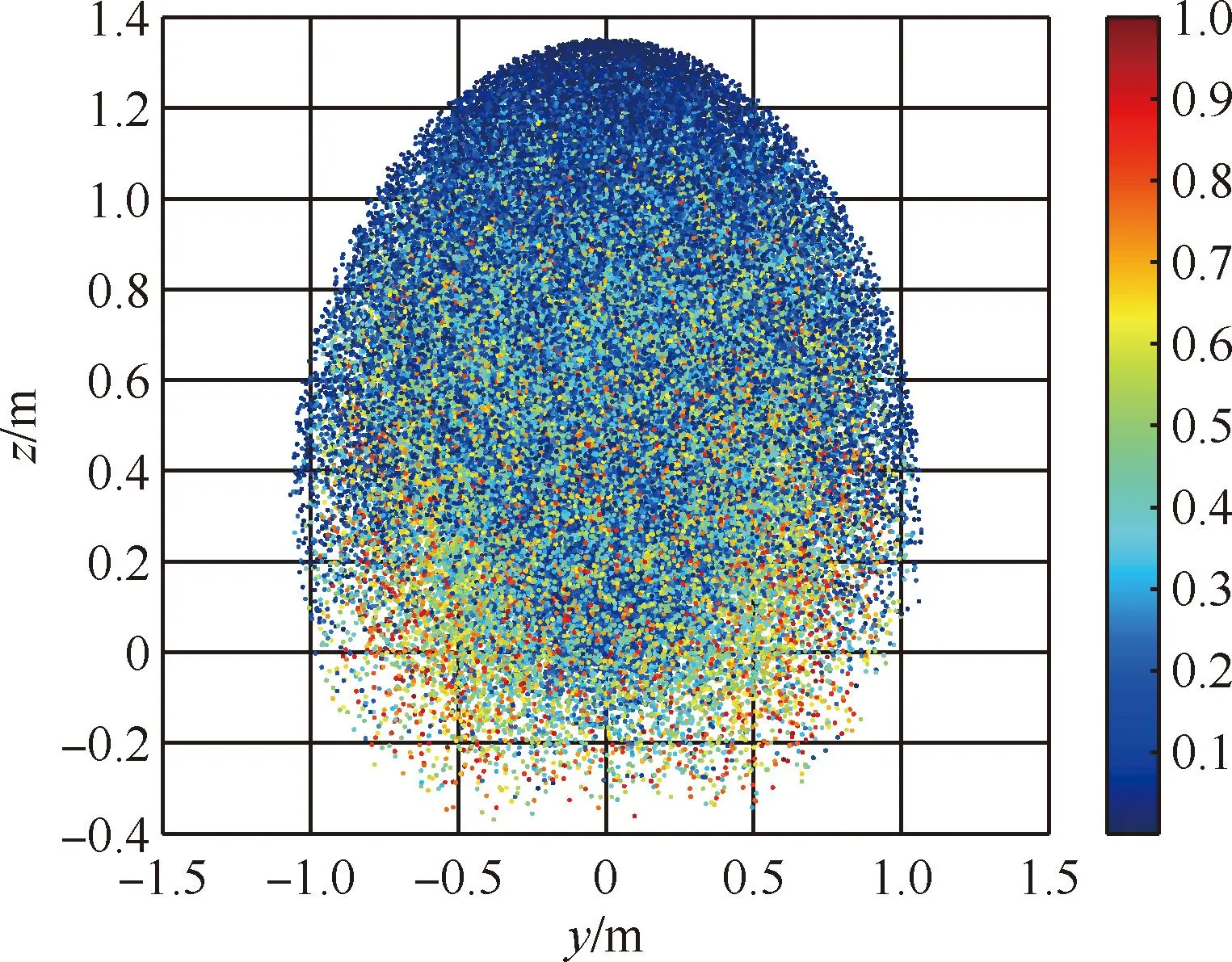
图8 Y-O-Z平面可操作度点云图Fig.8 Manipulability measure point cloud of Y-O-Z plane
3.2 算法实验验证
在机械臂第4关节运动范围为0~3.05 rad基础上,假设关节4靠近最小关节极限位置,同时设置其他关节角度适当大小以确保在初始位置P0时机械臂接近奇异状态,因此假设P0位置处7个关节角度用弧度表示分别为:0,-0.174 53,-1.221 73,0.087 27,-0.261 80,-2.443 46,-0.698 13。
根据机械臂正运动学得到机械臂末端坐标系原点的初始位置坐标为
P0(-0.123 085,0.174 492,1.149 312)
假设机械臂末端沿x和y正方向移动0.2 m,z方向保持不动,并保持末端姿态不变。得到的终止位置的坐标为
P1(0.076 915,0.374 492,1.149 312)
首先采用普通伪逆法求解关节速度,通过软件仿真各个关节角度在1 s内的变化,得到的仿真结果如图9所示。可见,大概在0.65 s处多个关节角度发生关节突变,导致关节1、关节3和关节4后续运动超出了关节极限。发生突变前7个关节角度(弧度)数据如下:0.740 79,-0.102 41,-1.976 46,0.289 61,-0.091 14,-2.135 99,-0.487 98。
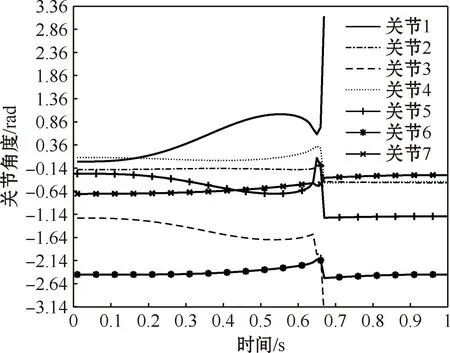
图9 伪逆法关节角度随时间变化曲线Fig.9 Curve of joint angle changing with time by pseudo inverse method
计算机械臂在此关节角度下的可操作度O(θ)。首先计算当前位姿下的雅可比矩阵J:
计算当前位姿下的可操作度为
可操作度非常接近0,此时机械臂是处于奇异状态的,并且关节角度突破了关节极限的限制,因此这种求解方法不适用于机械臂处于奇异并且关节角度接近关节极限时的情况。
下面在真实的机械臂上对式(25)进行验证。采用阻尼最小二乘法的方法进行避奇异,通过实时计算求解每个位置的阻尼系数λ进行关节速度求解,并且通过自运动来防止机械臂的关节到达极限位置。机械臂初始位置和终止位置(图10)与前面仿真的数据保持一致。

图10 机械臂初始位置和终止位置Fig.10 Initial position and terminal position of the manipulator
得到的关节角度随时间变化关系如图11所示。
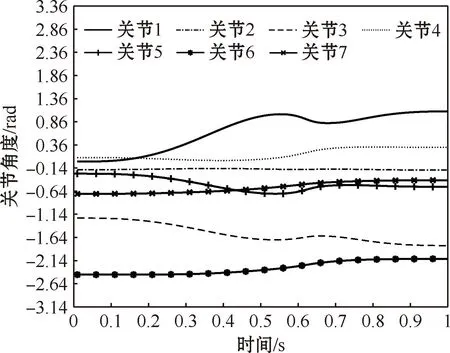
图11 两种方法结合的关节角度随时间变化曲线Fig.11 Curve of joint angle changing with time by combining two methods
由图11可知,得到的关节速度没有发生突变,同时关节4也没有超出最小关节极限,速度在1 s内也较为平缓,验证了阻尼最小二乘法和自运动结合的可行性。
3.3 自运动的验证
3.2节中采取了阻尼最小二乘法和自运动相结合的方法来求关节速度。为了验证所提出式(22)的自运动计算方法的正确性,需排除阻尼最小二乘法对自运动的干扰。考虑Diana7机械臂的关节极限,假设关节1接近极限位置,在此基础上设置其他关节使机械臂远离奇异状态,消除了阻尼最小二乘法的影响,假设7个关节初始角度(弧度)为:-3.054 33,-0.174 53,0,1.221 73,-0.261 80,-1.745 33,-0.698 13。
根据正运动学得到机械臂末端对应的位置坐标为
Pm(-0.467 230,0.010 210,0.956 054)
让机械臂沿y正向移动0.2 m,因此设置终止位置的坐标设为
Pn(-0.467 230,0.189 790,0.956 054)
通过进行添加和不添加自运动的两次实验来验证自运动正确性。其中,添加自运动的实验按照式(25)计算关节速度;未添加自运动的实验按照式(18)计算关节速度。
得到关节1的角度随时间变化关系如图12所示,由于机械臂未处于奇异状态,因此关节1即使在关节极限附近,也没有发生关节突变。关节1的最小关节极限为-3.12 rad,未添加自运动方法的关节角度变化如图中点划线所示,0.5 s后到达了关节1的最小关节极限,机械臂立即停止运动并且示教器报错。而图中实线为添加了自运动方法的关节角度变化情况,关节角度没有到达最小关节极限,从而验证了所提自运动关节速度计算方法的正确性。
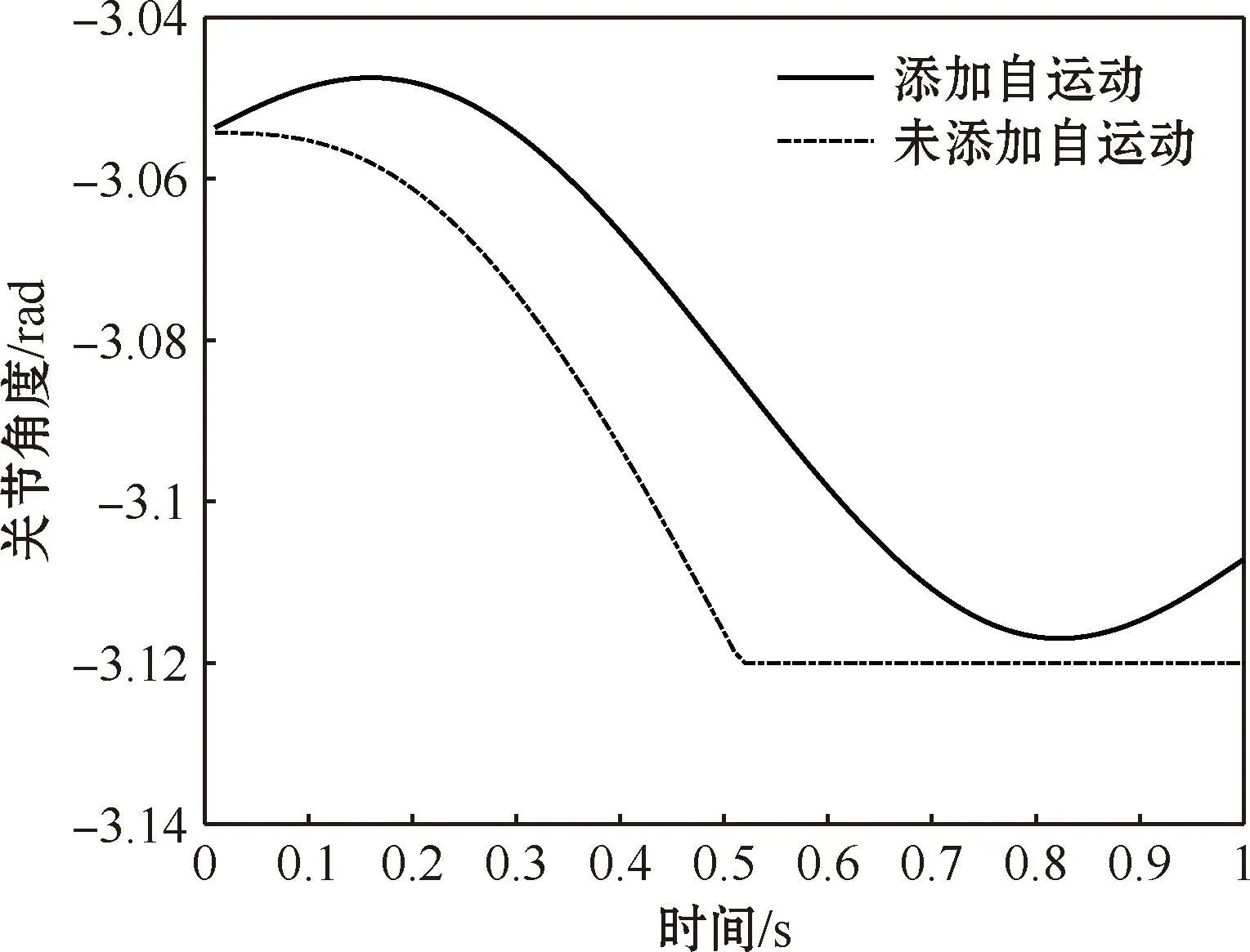
图12 关节1角度随时间变化关系Fig.12 The relationship between angle and time of joint 1
4 结束语
本文以七轴机械臂为研究对象,针对规划轨迹中存在奇异点的问题进行了研究。通过阻尼最小二乘法和零空间自运动计算方法,进行避奇异和避关节极限的双重操作,同时提出了新的自运动计算方法。实验结果表明,针对Diana7七轴机械臂,本文方法能够有效求解机械臂关节速度,在路径点存在机械臂奇异情况下能够使机械臂关节远离关节极限,有效调节关节速度以完成任务。后续的研究将聚焦到运动精度上,以满足各种场合下的任务需求。

