基于ISSA-ELM的垃圾发电厂焚烧过程建模方法研究
赵 征, 王 金, 周孜钰, 李倬舸, 魏 强
(1. 华北电力大学 控制与计算机工程学院, 河北保定 071003;2. 深圳能源环保股份有限公司, 广东深圳 518048)
符号说明:
CT1——一段翻动炉排翻动次数
CT2——二段翻动炉排翻动次数
CT3——三段翻动炉排翻动次数
CT4——四段翻动炉排翻动次数
CT5——五段翻动炉排翻动次数
CS1——一段滑动炉排滑动次数
CS2——二段滑动炉排滑动次数
CS3——三段滑动炉排滑动次数
CS4——四段滑动炉排滑动次数
CS5——五段滑动炉排滑动次数
C1——一段滑动炉排速度系数
C2——二段滑动炉排速度系数
C3——三段滑动炉排速度系数
C4——四段滑动炉排速度系数
C5——五段滑动炉排速度系数
tT1——一段翻动炉排等待时间,s
tT2——二段翻动炉排等待时间,s
tT3——三段翻动炉排等待时间,s
tT4——四段翻动炉排等待时间,s
tT5——五段翻动炉排等待时间,s
tS1——一段滑动炉排等待时间,s
tS2——二段滑动炉排等待时间,s
tS3——三段滑动炉排等待时间,s
tS4——四段滑动炉排等待时间,s
tS5——五段滑动炉排等待时间,s
H1——一段炉排料层厚度,mm
H2——二段炉排料层厚度,mm
vGN——一次风干燥风机转速,r/min
vQN——一次风气化风机转速,r/min
vEN——二次风机转速,r/min
QLHV——垃圾热值,kJ/kg
垃圾焚烧发电技术具有无害化、减量化、资源化的优势,是目前处理生活垃圾的最佳方式[1-2]。当前,提高焚烧效率及焚烧过程稳定性是垃圾发电厂运行的重要目标[3]。
垃圾发电过程十分复杂,一方面,该过程包含诸多子系统及大量的过程参数变量,其中除了温度、流量等连续变量外,还有炉排翻动次数、炉排滑动次数等难以调节的非连续变量;另一方面,由于垃圾成分复杂、热值波动大,且焚烧炉为慢对象,机组在调节过程中会处于很长时间的过渡状态。目前,垃圾焚烧炉自动投入率低,同样的运行工况下,不同的司炉人员操作会影响焚烧炉的燃烧效率。因此,筛选稳定工况数据,高效挖掘电站数据信息,从而建立垃圾发电厂焚烧过程稳态模型,对焚烧工况调整及为操作人员提供最佳操作变量值具有借鉴意义。
Magnanelli等[4]运用机理建模方法对垃圾焚烧炉焚烧过程进行了建模,但是存在推导过程复杂且精度低的问题。因此,燃烧过程建模中需大量运用数据驱动建模。尹成宇[5]采用反向传播(BP)神经网络建立了NOx排放浓度和锅炉热效率的模型,但BP神经网络存在易陷入局部极值、收敛速度慢等问题;彭道刚等[6]基于大数据和神经网络对锅炉燃烧含氧量建立了多输入单输出模型,并通过贝叶斯算法对神经网络进行改进,解决了经典神经网络易陷入局部最优、收敛速度慢的弊端;宋清昆等[7]基于某热电厂锅炉的实际运行数据,通过径向基函数(RBF)神经网络建立了锅炉燃烧系统的多输入多输出模型,与BP神经网络相比,RBF神经网络具有更优的分类能力和逼近能力,以及更快的学习速度;曾卫东等[8]基于最小二乘法和多项式拟合,建立了以垃圾发酵时间和入炉垃圾量为输入、锅炉蒸汽流量为输出的数学模型,为垃圾吊运人员对垃圾入炉量的控制提供了准确的指导;仲亚飞等[9]采用支持向量机建立了某660 MW机组的锅炉排烟温度模型,为锅炉的运行提供了指导。
Huang等[10]在单隐藏层前馈神经网络的基础上提出极限学习机(ELM)。ELM的输入层权重和隐藏层偏置随机生成,相比于传统神经网络,ELM结构简单、便于使用、学习速度快、隐含层和输出层之间的连接权值不需要迭代调整。但由于ELM输入层权重和隐藏层偏置随机选取,对模型稳定性造成一定影响。Xue等[11]提出一种新兴群智能算法——麻雀算法(SSA),SSA具有求解精度高、稳定性好、收敛速度快等优点。王琳蒙等[12]提出基于反向学习的SSA,丰富了SSA初始种群多样性,提高初始种群质量,但仍存在局部搜索能力差等缺点。
笔者以某垃圾焚烧炉历史运行数据为基础,提出一种基于层次分析法的改进麻雀算法(ISSA),从而进一步提高SSA的全局搜索能力。利用SSA的高求解精度优化ELM输入层权重与隐藏层偏置,最终建立基于ISSA-ELM的垃圾发电厂焚烧过程稳态模型。同时,将该模型与传统模型进行比较,以验证其精度。
1 垃圾焚烧炉基本结构
该垃圾焚烧炉由五段机械炉排构成,其中第一、第二段为干燥炉排,第三、第四段为燃烧炉排,第五段为燃尽炉排[13]。每段燃烧炉排包含滑动炉排、固定炉排和翻动炉排。滑动炉排使垃圾在炉排上缓慢地向前滑动;翻动炉排用于翻动和搅拌炉内的垃圾,破碎垃圾焚烧时在其表层上会形成熔融层,使得更多的垃圾与助燃空气接触,从而得以充分燃烧。风系统包括一次风系统和二次风系统。一次风从垃圾储蓄池抽取,由空气预热器加热至180 ℃左右,送入焚烧炉的底部,通过焚烧炉炉排片之间的间隙,穿透垃圾床层进入到焚烧炉膛内,与垃圾混合燃烧;同时建立垃圾池负压,防止垃圾臭气外溢,实现臭气的有效治理。二次风主要用于调节氧量,以保证更好地燃烧[14]。针对国内垃圾水分多、不可燃物含量高和热值低的特点,大部分炉排式垃圾焚烧炉采用了炉膛后拱前倾的设计,形成较好的空气动力场,利于燃烧,如图1所示。
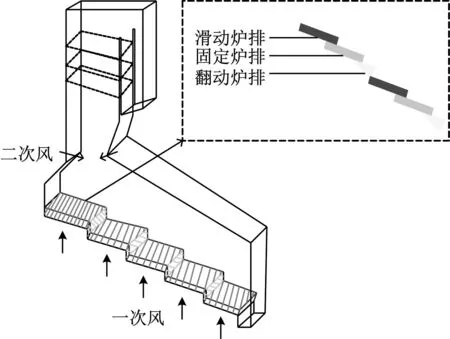
图1 焚烧炉结构图
2 基本方法原理
2.1 Lasso算法
Lasso算法是1996年首次被提出的基于惩罚的变量选择方法[15]。利用Lasso算法进行变量选择,可以有效去除冗余变量,解决模型过拟合问题,进一步简化模型,提高模型的建模精度。该算法以参数集β=(β0,β1,…,βp)为研究对象,在最小二乘线性回归的基础上增加惩罚项,对估计参数β进行压缩,当被压缩参数缩小至一个阈值时,令其为零,以实现变量选择。
典型的线性回归模型可表示为有n组观测值,每组观测值由p个输入变量xi=[xi1,xi2,…,xip]T和1个输出变量yi组成,可设为:
(1)
式中:xij为相关预测变量;ei为松弛变量。
采用最小二乘目标函数J进行最小化求解:
(2)
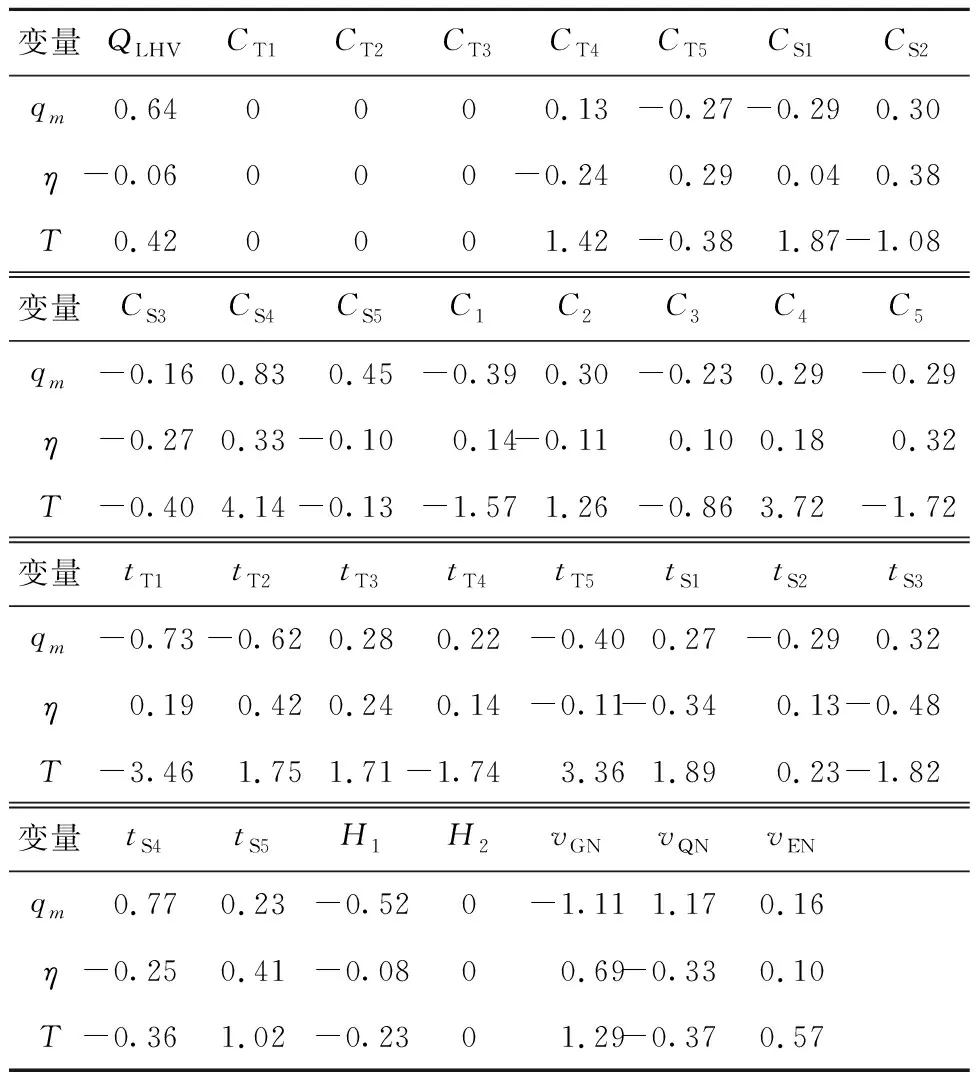
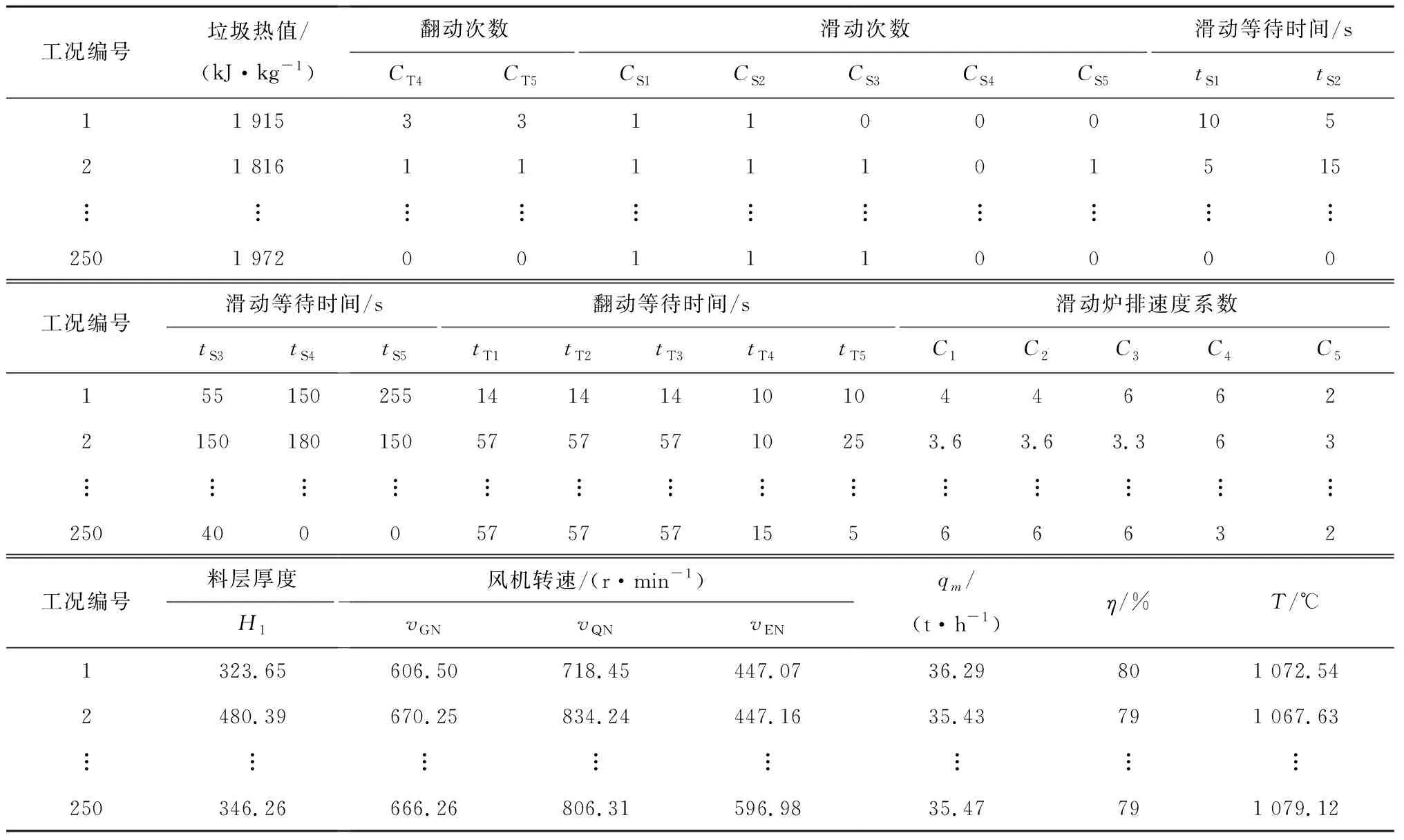
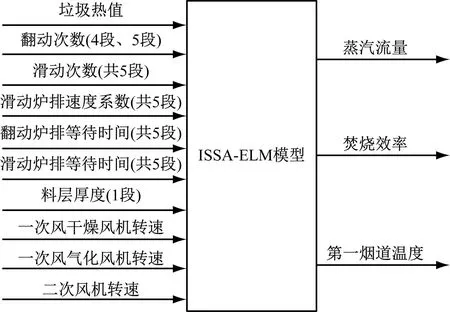
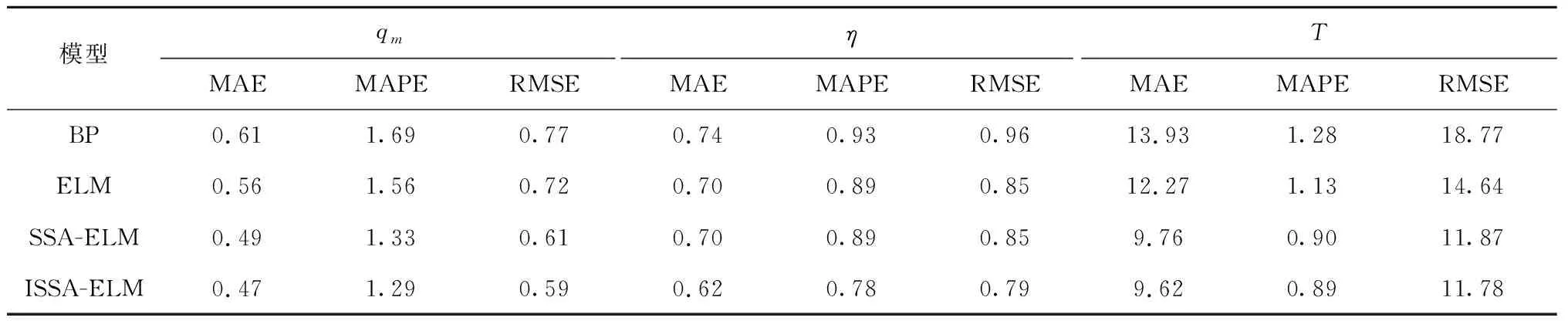
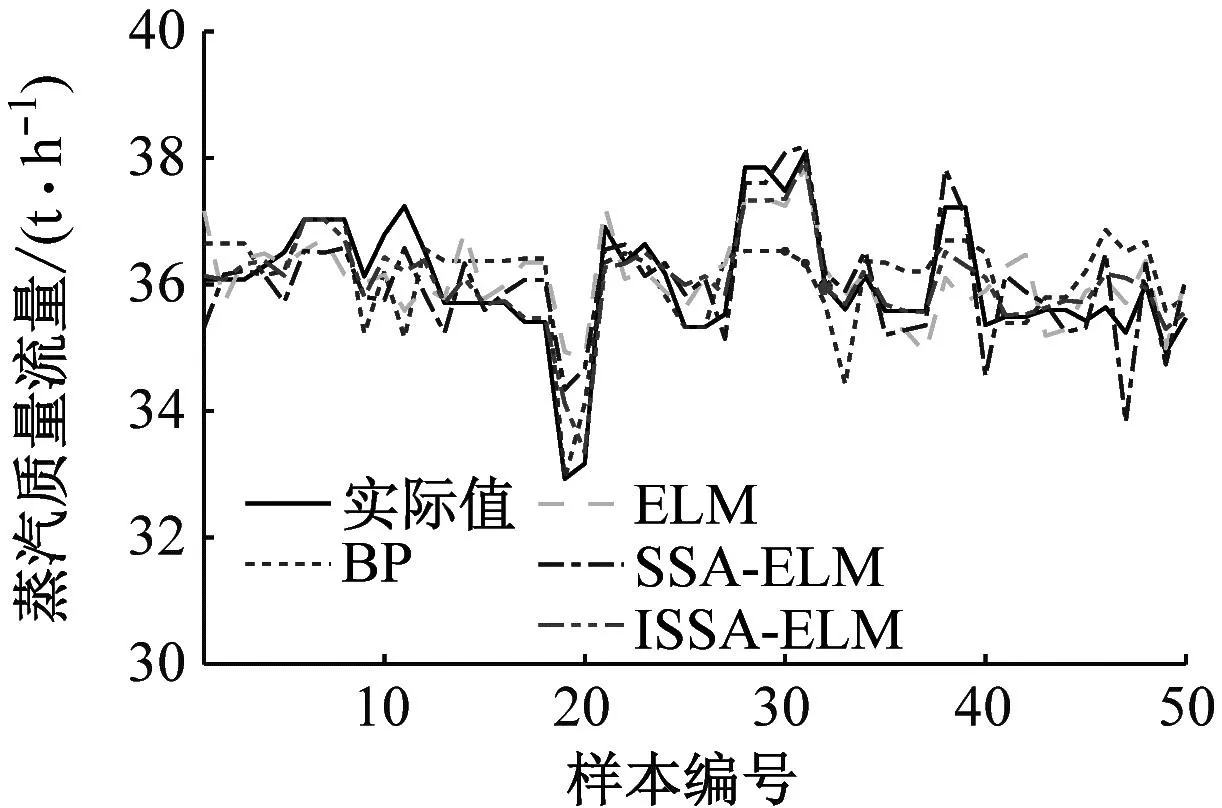
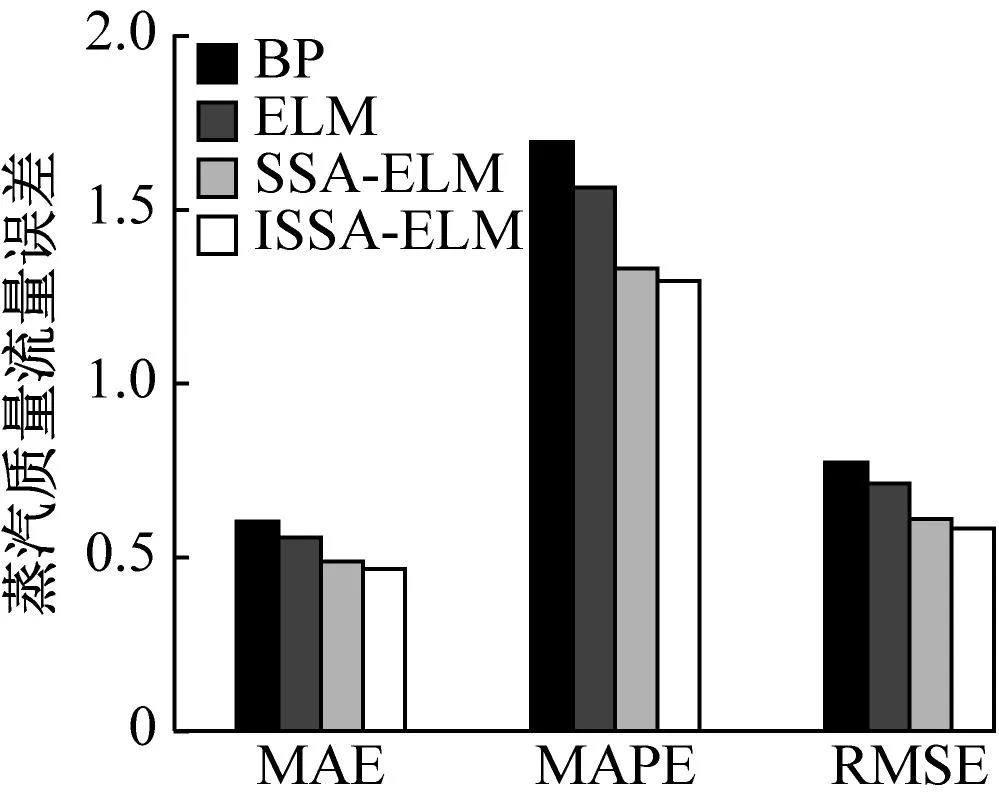
一般式中β的最小二乘估计均不为0,且若n (3) s.t. ‖βj‖≤t ELM是一种单隐藏层前馈神经网络算法。ELM的输入层权重和隐藏层偏置随机选取,依据广义逆矩阵(MP)理论计算解析求出输出层权重[16]。ELM的网络结构如图2所示。对于n组观测样本,设网络结构的隐藏层节点数为k,输入层节点数仍为p,输出层节点数为m,激活函数为g(·),则有: (4) 图2 ELM结构示意图 (5) 式中:yij为第i组观测样本的输出变量;wj为输入权重系数;bj为偏置系数;ωj为输出权重系数;oj为隐藏层输出值。 式(5)可简写为: Hω=Y (6) 式中:H为隐藏层输出矩阵。 (7) 式中:H+为H的广义逆矩阵。 与传统神经网络相比,ELM虽然可以有效解决计算复杂度大和训练参数时易陷入局部最优解的问题,但由于ELM的输入权重和偏置随机确定,因此模型稳定性较差。引入SSA优化ELM模型的初始参数,提高模型稳定性及模型精度。 SSA通过模拟麻雀的觅食行为和反捕食行为寻找优化问题的最优参数[17],设麻雀种群U为: (8) 式中:uij为麻雀个体;h为麻雀数量;d为待优化问题的变量维度。 设群体适应度函数Fu为: (9) 式中:f为个体的适应度值。 发现者的位置Uij,μ+1更新为: (10) 式中:μ为当前迭代次数;α∈(0,1]为随机数;Imax为最大迭代次数;Uij为第i个麻雀在第j维中的位置;R2∈[0,1]为预警值;S∈[0.5,1]为安全值;Q为随机数,服从正态分布;L为1×d的矩阵,该矩阵内每个元素均为1。 加入者的位置更新为: (11) 式中:us为当前发现者占据的最优位置;uworst为当前全局最差的位置;A为1×d的矩阵,该矩阵内每个元素随机赋值为1或-1,A+=AT(AAT)-1。 当第i个加入者的适应度值较低时,无法获得食物,需飞往其他地方获取更高的能量。 警戒者的位置更新为: uij,μ+1= (12) 式中:ubest为当前全局最优位置;γ为步长控制参数;K∈[-1,1]为随机数;fi为当前麻雀个体的适应度值;fg为当前全局最劣的适应度值;fs为当前全局最佳的适应度值;ε为最小常数,以避免分数为0。 层次分析法(AHP)是一种权重决策方法,具有定性与定量相结合等特点。针对SSA容易陷入局部最优的问题,引入AHP对其进行优化,平衡算法全局探索能力与局部开发能力,增强算法局部搜索能力,使算法性能得到进一步提高。 将式(11)改进为 uij,μ+1= (13) 式中:a、b为标度参数。 将a、b按Saaty标度法 (见表1)进行重要性程度等级评定,按比较结果构成判断矩阵A=[1,1/3;3,1]。计算判断矩阵A的最大特征值λmax及其对应的特征向量,将特征向量进行归一化后记为W=[0.25;0.75],W的元素为整体极值与局部搜索范围2个指标对加入者位置影响重要性的排序权值,能否确认该排序,需进行一致性检验。其中,r阶一致矩阵的唯一非零特征根为r;r阶正反互阵A的最大特征根λ>r,当且仅当λ=r时,A为一致矩阵。 表1 Saaty标度表 定义一致性指标为: (14) C为0时,有完全的一致性;C接近于0,有满意的一致性;C越大,不一致性越严重。本次实验通过一致性检验,故a=0.25,b=0.75。 ISSA-ELM算法的迭代流程如图3所示。 图3 ISSA-ELM算法迭代流程图 在建立焚烧模型前,应确定模型的输入变量和输出变量。综合考虑安全性、稳定性和经济性3个方面的焚烧炉控制需求,首先选取蒸汽质量流量qm、焚烧效率η、第一烟道温度T作为模型输出变量。其中,蒸汽流量和第一烟道温度为直接测量得到,垃圾发电厂的焚烧效率一般通过反平衡法计算得到[18],计算公式如下: (15) 其中,qi代表第i项热损失;q2为排烟热损失;q3为气体未完全燃烧热损失;q4为固体未完全燃烧热损失;q5为散热损失;q6为灰渣物理热损失。 除机理分析外,通过Lasso算法对变量进行筛选,Lasso算法通过引入惩罚函数的方式将影响较小的变量系数压缩为0,从而将这些变量剔除,通过十折交叉验证,取λ=0.5时,得到各个变量的Lasso拟合系数见表2。 表2 Lasso拟合系数 其中,由于一、二、三段翻动炉排的翻动次数(CT1、CT2、CT3)、二段炉排料层厚度(H2)的拟合系数收敛为0,故最终确定输入变量为:垃圾热值、四段翻动炉排翻动次数、五段翻动炉排翻动次数、滑动炉排滑动次数(共5段)、滑动炉排速度系数(共5段)、滑动炉排等待时间(共5段)、翻动炉排等待时间(共5段)、一段炉排料层厚度、一次风干燥风机转速、一次风气化风机转速、二次风机转速。 对蒸汽流量、汽包压力、水平烟道出口含氧量进行稳态判定。首先将参数归一化,然后计算各参数的误差指标,即 (16) 式中:Fmax为一段时间内参数的最大值;Fmin为一段时间内参数的最小值;F为参数的额定值;δ为给定阈值。 设置判定稳定数据段的滑动窗口长度为3 600 s,若该窗口内的数据满足式(16),则认为该数据段为稳定数据段,若不满足,则窗口向前滑动,继续进行稳定工况判定。建模部分稳定数据见表3。 表3 焚烧炉部分稳定数据 建立垃圾发电厂焚烧过程模型的步骤如下: (1) 利用滑动窗口筛选出的稳定数据,然后将数据进行归一化处理,并划分80%数据为训练集,20%数据为测试集。 (2) 根据所选垃圾发电厂焚烧过程模型的输入变量数量确定ISSA-ELM模型的输入层节点数(p=27),以十折交叉验证为准则,确定隐含层节点数(k=20),采用Sigmoid激活函数,得到ISSA-ELM模型,如图4所示。 图4 焚烧炉焚烧过程ISSA-ELM模型 (3) 设置种群数量、最大迭代次数、发现者数量、警戒者数量等,并初始化种群。 (4) 计算初始适应度值进行排序,根据式(10)、式(12)、式(13)更新麻雀位置,并计算适应度值。 (5) 判断是否满足搜索结束条件,若满足条件则结束搜索;若未满足则继续进行搜索寻优。 (6) 结束寻优获得ELM模型最优权重和阈值,计算隐藏层输出。 (7) 将建模测试数据的输入信息输入最优ELM模型中,得到模型输出值。 本文采用的模型评价指标为平均绝对误差(MAE,emae)、平均绝对百分比误差(MAPE,emape)、均方根误差(RMSE,ermse)。 MAE反映了模型输出值和实际值之间绝对误差的大小;MAPE反映了模型输出值偏离实际值的程度;RMSE反映了模型输出值和实际值之间差异的样本标准差,体现样本的离散程度。三者结合更能反应模型的精度。3种评价指标的数据越小代表模型精度越高,其计算公式如下: (17) (18) (19) 为验证ISSA-ELM模型的有效性,采用ISSA-ELM、SSA-ELM、ELM、BP神经网络对焚烧炉燃烧过程进行建模,并与ISSA-ELM模型的建模结果进行对比分析。在其他条件保持不变的情况下,建模结果及误差分析如图5、图6所示,不同模型对建模精度的影响见表4。 表4 不同模型对建模精度的影响 (a) 蒸汽质量流量 (a) 蒸汽质量流量 由图5、图6和表4可以看出,在模型精度方面,以蒸汽质量流量为例,BP神经网络、ELM、SSA-ELM和ISSA-ELM的MAE分别为0.61、0.56、0.49和0.47,故模型精度由低到高排序为BP 与此同时,在模型稳定性方面,引入ISSA优化ELM模型的初始参数,可解决由于ELM的输入权重和偏置随机确定导致ELM模型稳定性较差的问题,ISSA可以以较快的速度找到ELM模型的建模最优参数,从而降低算法优化时间,提高迭代效率,提高模型稳定性。 (1) 提出了一种基于ISSA-ELM的垃圾发电厂焚烧过程建模方法,引入AHP对SSA进行改进,平衡了算法全局探索与局部开发能力。通过ISSA优化ELM模型的初始参数,解决了由于ELM的输入权重和偏置随机确定导致ELM模型稳定性较差的问题,提高模型稳定性及模型精度。 (2) 建立基于ISSA-ELM的垃圾发电厂焚烧过程模型,通过与BP神经网络、ELM模型、SSA-ELM模型进行对比分析可知,在模型的准确性、稳定性、快速性等方面,ISSA-ELM 模型具有更优的性能。说明该模型能够更加准确地反映垃圾发电厂焚烧过程的输入输出关系,对提高垃圾发电厂的焚烧效率及焚烧过程稳定性和环保性具有指导意义。
2.2 ELM
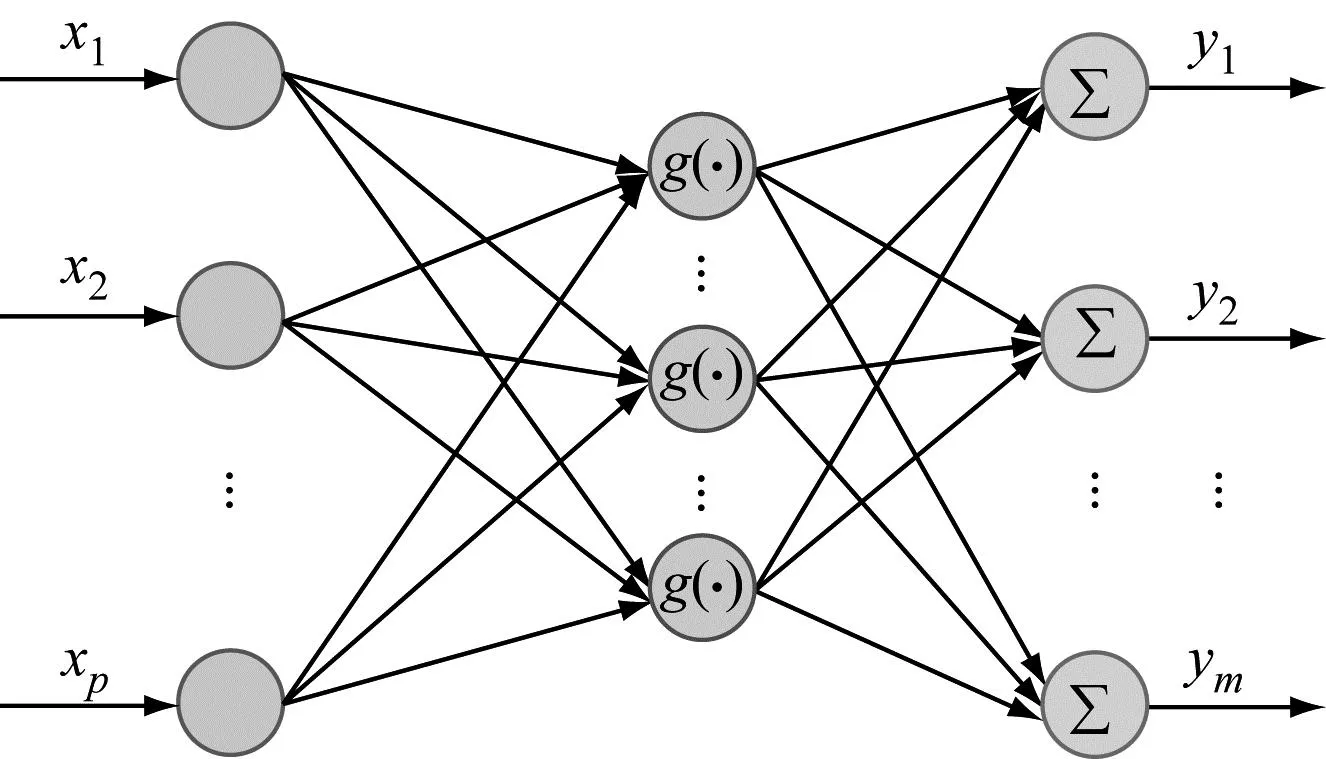
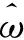
2.3 SSA
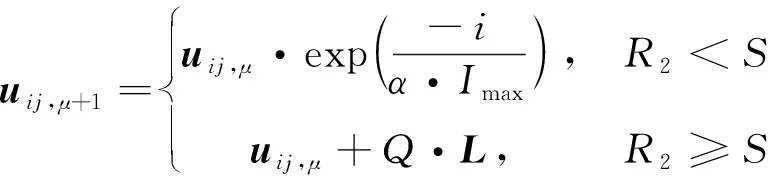
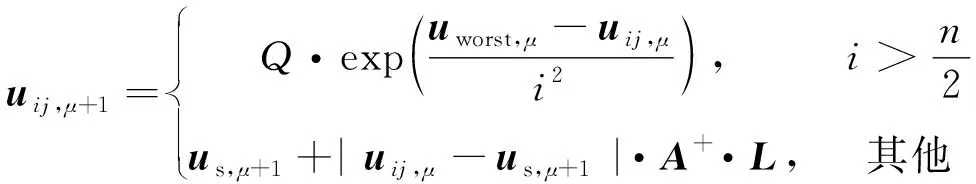
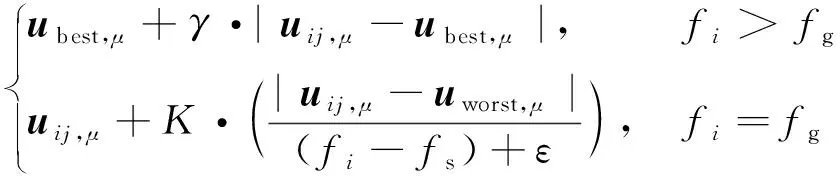
2.4 ISSA
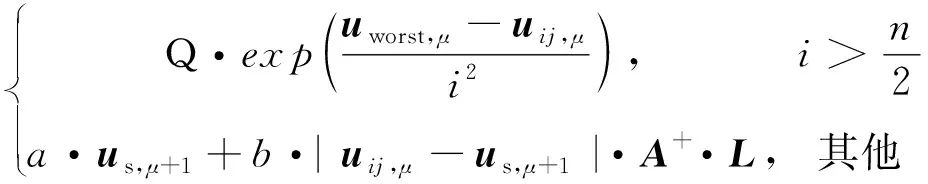
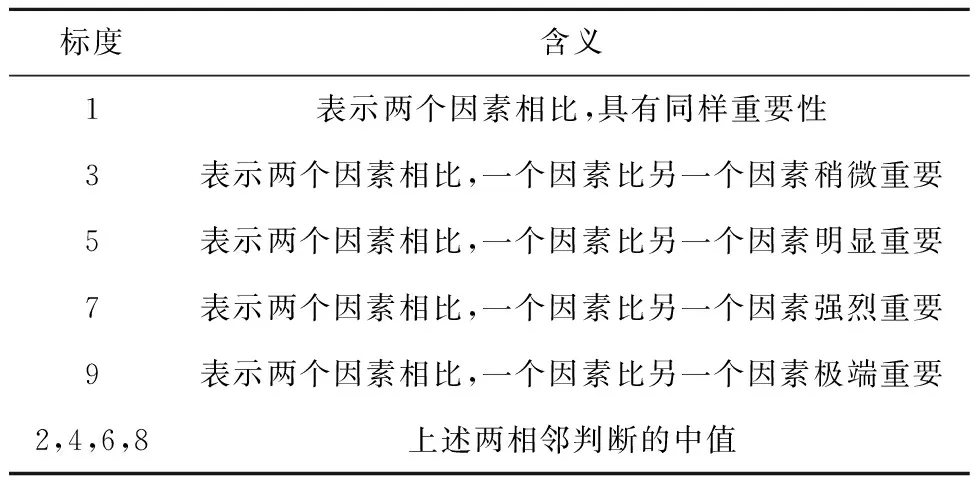
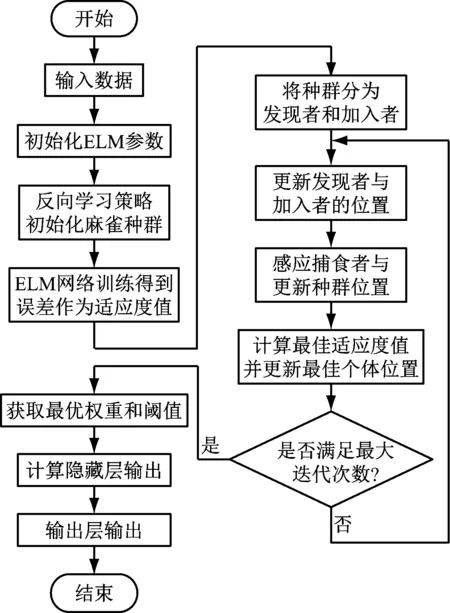
3 基于ISSA-ELM的垃圾发电厂焚烧过程模型
3.1 变量选择
3.2 稳定数据段筛选
3.3 模型建立
4 建模结果与分析
4.1 模型评价指标
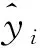
4.2 结果分析
5 结 论
——国外课堂互动等待时间研究的现状与启示

