长联大跨连续梁车桥耦合动力响应分析
蔡军哲 司龙
1.陕西城际铁路有限公司 西安710016
2.陕西省西安市长安区交通运输局 710100
引言
当列车通过桥梁时,因列车自身动力特性的作用、轨面不平顺、线路曲线半径及轮轨关系的影响,引起列车弹簧上部由车身及乘客所构成的悬挂质量的振动。车辆的振动会促使桥梁结构发生振动,导致桥梁结构内力及位移变化,与此同时桥梁结构的振动又促进车辆的振动,这种相互作用和反作用就是“车桥耦合”问题[1]。
车桥耦合振动研究可追溯到1929 年的Jeffcott[2]发表的动载荷作用下桥梁振动的研究。初期的研究都是将车辆简化为移动的载荷,在1968 年,Tan 和Shore[3,4]运用一个移动常量力来考虑而忽略其惯性,当车辆的质量远小于桥梁结构且桥面平整度较好时,上述简化研究还是很实用和便捷的。但当车辆的质量不可以忽略时,就需要使用改进的模型。在1979 年,Blewjas[5]提出了移动质量模型,但这一模型在反映车桥耦合本质上仍然是不完善的。林海等[6]对初期的解析有更详细的介绍。李乔等[7]运用车桥耦合振动理论进行铁路曲线连续梁桥车桥耦合振动响应分析。凌知民等[8]在车桥耦合振动研究的基础上,对比分析高墩连续梁桥实测结果。
本文采用23 自由度的二系四轮对车辆模型和桥梁模型,建立及求解车桥耦合系统动力平衡方程。以某渭河特大桥(50 +8 ×100 +50)m连续梁为例,采用大型有限元模拟的方法,建立长联大跨连续梁的车桥耦合模型,基于轨面随机不平整激励作用下,计算了B 型车以60km/h、80km/h、100km/h及120km/h四种不同速度通过连续梁桥时车桥耦合响应。
1 计算模型和分析方法
车桥耦合的动力响应分析是一个复杂的课题,由于列车在桥梁上运行位置的不断变化从而使得该系统的振动具有时变特性,因此一般在时域内进行分析。对于这样的时变非线性系统,首先建立了车辆模型、桥梁模型,并将它们组合形成车桥耦合系统动力相互作用分析模型,通过数值分析求解。
1.1 列车动力学模型
以车辆前进方向为X轴的正向,竖向向下为Z轴正向,Y轴按右手定则确定,绕3 个坐标轴旋转的正向也由右手定则确定,车辆模型采用二系悬挂四轮对的车辆单元由1 个车体、2 个转向架、4 个轮对组成,这些构件之间由弹簧和阻尼器连接。每车体和每转向架均具有Y、Z、RX、RY、RZ共5 个方向的自由度,每轮对具有Y、RZ共2 个方向的自由度。每个车辆单元共有23 个自由度。车辆模型见图1。
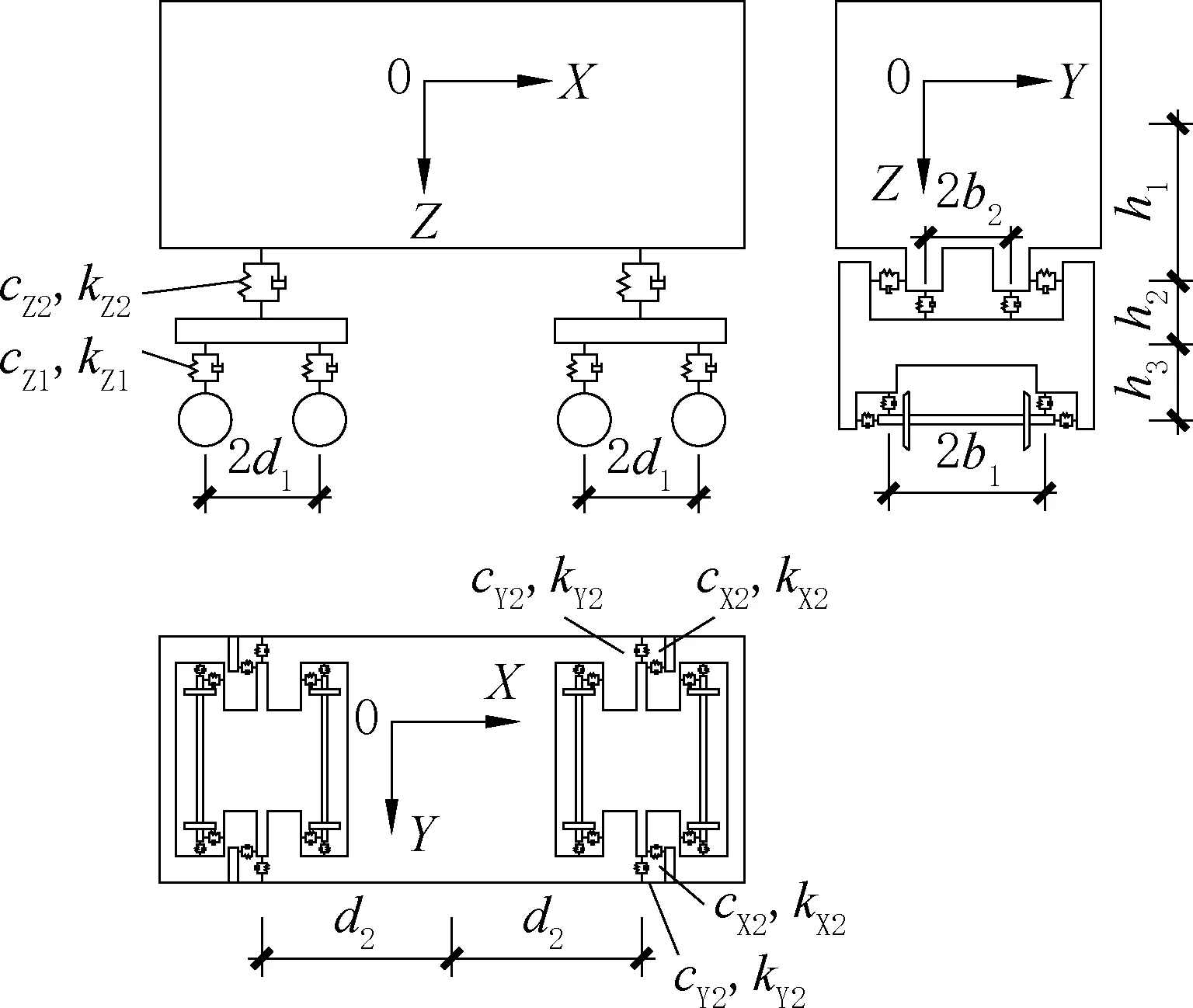
图1 二系四轮对车辆模型Fig.1 Two series four wheel set vehicle model
车辆单元的总势能V、总阻尼耗能R、总动能T可由车体、转向架和轮对的加速度表示。可得车辆子系统的动力方程:
式中:MV、CV、KV为车辆的质量、阻尼、刚度矩阵;XV、FV分别为车辆位移向量和力向量。XV=(Y1Z1RX1RY1RZ1Y2Z2RX2RY2RZ2Y3Z3RX3RY3RZ3Y4YZ4Y5RZ5Y6RZ6Y7RZ7),其中,1 表示车体,2、3 分别表示前、后转向架,4、5 表示与前转向架相连的第一和第二个轮对,6、7 表示与后转向架相连的第三和第四个轮对。
1.2 桥梁力学模型
桥梁子系统的动力方程为:
式中:MB、CB、KB为桥梁子系统的总体质量矩阵、总体阻尼矩阵、总体刚度矩阵;XB、FB为桥梁位移向量和力向量。
桥梁子系统总体质量矩阵和总体刚度矩阵由有限元计算,总体阻尼矩阵采用Rayleigh 阻尼由比例阻尼求得;桥梁子系统的力向量为轮轨间作用力,FB为车辆对桥梁作用力之和。
1.3 轨道不平顺
轨道不平顺为轨道上一系列离散点处左、右轨中心点与其理论位置的距离。车辆通过时,轨道不平顺使轮对发生附加位移、附加速度和附加加速度,附加速度和附加加速度导致车桥系统产生振动。轨道不平顺的附加速度和附加加速度按式(3)计算:式中:E为轨道不平顺,表示任一组轨道不平顺离散数值;ν 为车辆运行速度;t为车辆运行时间;ΔX为车辆运行距离变化量。
1.4 轮轨间相互作用关系
轮轨间相互作用力作用于左右轮轨接触点,在Z方向上,作用力的数值由轮轨密贴理论确定,在Y方向上,作用力的数值由Kalker蠕滑理论确定。F1、F2为转向架与轮对之间Z方向的相互作用力,F3、F4为轮对与轨面之间X方向的相互作用力,F7、F8、F9、F10为轮对与轨面之间Z方向的相互作用力,F5、F6为轮对与轨面之间Y方向的相互作用力,G为静轴重。竖向、横向轮轨间相互作用关系见图2。

图2 轮轨间相互作用关系Fig.2 Wheel rail interaction
1.5 车桥耦合系统方程的建立
车辆和桥梁子系统通过轮轨接触关系联系起来,轮轨之间的位移协调和受力平衡可以确定车辆、桥梁的相互作用力[9,10]。上述桥梁、车辆动力方程右端的力的向量FB和FV是桥梁、车辆运动和轨道不平顺的函数,将力向量FB和FV中与桥梁、车辆运动有关的项移动至方程左端,车桥耦合系统动力平衡方程为:
式中:MVV=MV、MBB=MB分别为车辆、桥梁质量矩阵;CVV、CVB、CBV、CBB分别为车辆、车-桥、桥-车及桥梁的阻尼矩阵;KVV、KVB、KBV、KBB分别为车辆、车-桥、桥-车及桥梁的刚度矩阵;FVB和FBV分别为作用在车辆、桥梁上与轨道不平顺有关的力向量;XV、XB分别为车辆、桥梁位移向量;分别为车辆、桥梁速度向量;分别为车辆、桥梁加速度向量。
车桥耦合系统运动平衡方程采用Newmark-β法求解,车桥耦合计算流程见图3 所示。

图3 车桥耦合计算流程Fig.3 Vehicle-bridge coupling calculation flow
2 计算参数
2.1 列车类型及编组
列车采用B型车6 节编组,考虑实际运营中可能的列车运行速度,为研究行车速度与车桥耦合振动的关系,行车速度取60km/h~120km/h,每20km/h一个速度等级。
2.2 桥梁模型及自振特性
(50 +8 ×100 +50)m连续梁采用单箱单室变高度直腹板箱形截面见图4,中支点梁高6.6m,跨中梁高3.2m,箱梁顶宽9.2m,底宽5.5m,悬臂端厚20cm,悬臂根部厚65cm。箱梁腹板厚43cm~80cm,底板厚32cm~70cm,顶板厚32cm。采用MIDAS Civil 软件建立全桥三维空间有限元模型见图5,经桥梁自振特性分析,连续梁各工况时程积分的时间步长设置为列车运行0.25m所需的时间。桥梁系统的阻尼按Rayleigh阻尼考虑,偏安全考虑连续梁桥各阶频率相应的阻尼比均取0.02。一阶横向和竖向频率为分别为0.591Hz和1.013Hz。

图4 桥梁断面图(单位:cm)Fig.4 Bridge section drawing(unit:cm)

图5 全桥有限元模型Fig.5 Finite element model of overall bridge
2.3 轨道不平顺
轨道不平顺为实际轨道接触面沿轨道长度方向与理论平顺轨面数值之间的差值,受波长、相位和幅值随机叠加而成。模拟轨道不平顺方法主要有三角级数法、二次滤波法和白噪声滤波法等,其中三角级数法具备良好的通用性,精度高、计算速度快,并使用数值积分变步长的要求。本文通过三角级数模拟轨道不平顺,采用德国低干扰谱转换时域样本。波长取1m~80m,该时域样本中方向、高低、水平幅值依次为5.20mm、6.84mm 和3.31 ×10-3rad;轨道不平顺时域曲线的前1000m见图6。

图6 无砟轨道不平顺谱转换的时域样本Fig.6 Time domain samples of irregularity spectrum conversion for ballastless track
3 车桥耦合振动分析
由上述车辆、桥梁相关参数、轨道不平顺样本,计算了B型车以60km/h、80km/h、100km/h及120km/h四种不同速度通过渭河特大桥时车桥耦合动力响应。
3.1 桥梁响应
图7 为列车速度与桥梁横向位移的变化情况,横向位移中跨跨中值依次大于墩顶和边跨跨中值。边跨跨中横向位移和车速成线性增加,车速越大位移越大;中跨跨中横向位移随车速递增先增加后减小,速度在80km/h、100km/h 时,横向位移分别为0.081mm、0.083mm,达60km/h时0.043 两倍;墩顶横向位移随车速递增先增加后减小,在100km/h时达到最大。

图7 车速与桥梁横向位移曲线Fig.7 Speed and bridge lateral displacement
图8 为列车速度与桥梁横向加速度的变化情况,横向加速度值中跨跨中值依次大于边跨跨中和墩顶值。跨中横向加速度随车速递增先增加后减小,100km/h对应的值是80km/h 的2倍,并达到最大48.55mm/s2、38.485mm/s2。墩顶横向加速度变化范围不大,说明车速对其影响较小。

图8 车速与桥梁横向加速度曲线Fig.8 Speed and bridge lateral acceleration
图9 为列车速度与桥梁竖向位移的变化情况,桥梁竖向位移随速度的增加而增加,其变化范围不大,且在时速120km/h出现最大值,其中中跨跨中竖向位移为27.2mm,边跨跨中竖向位移为5.6mm。

图9 车速与桥梁竖向位移曲线Fig.9 Speed and bridge vertical displacement
图10 为列车速度与桥梁竖向加速度变化情况,桥梁竖向加速度与列车速度呈线性增加,速度越高竖向加速度越大,其中120km/h对应的值是60km/h的5 倍左右。

图10 车速与桥梁竖向加速度曲线Fig.10 Speed and bridge vertical acceleration
在车桥耦合响应研究中,动力放大系数是较重要的参数,其定义为同一截面竖向动位移与竖向最大静态位移的比值。不同速度下中跨跨中竖向位移的动态放大系数随速度增加而增加,见图11。
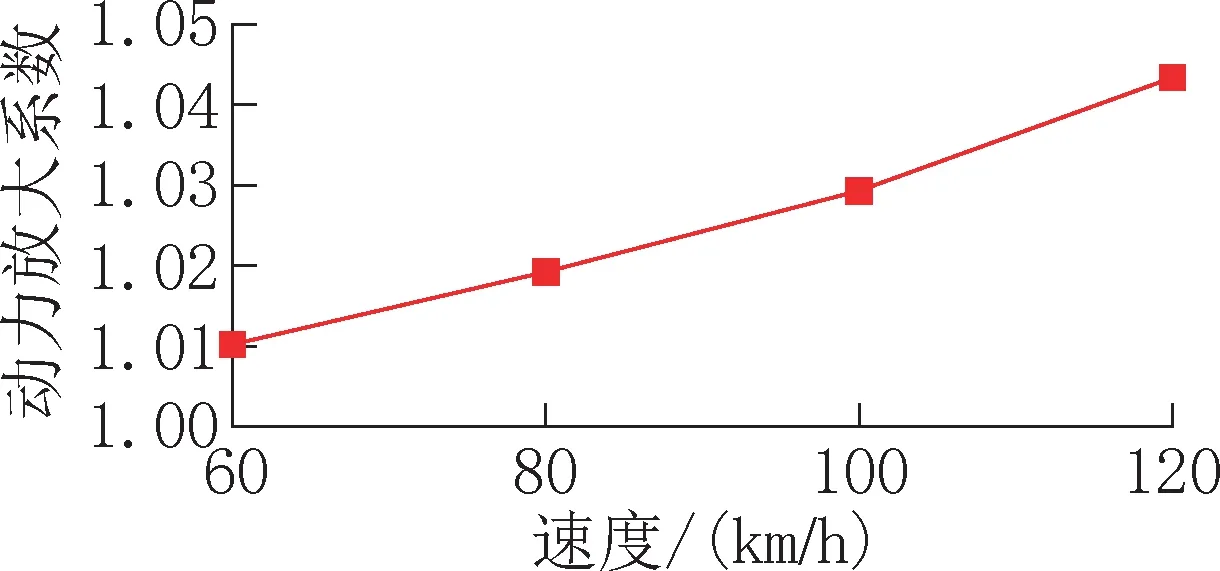
图11 车速与桥梁动态放大系数曲线Fig.11 Speed and bridge dynamic amplification coefficient
3.2 车辆响应
对于车辆振动响应的评价主要有运行稳定性和运行平稳性两项。运行稳定性是评价车辆安全性指标,主要通过脱轨系数、轮重减载率及轮轴横向力判定。运行平稳性是评价乘车平稳性的指标,主要通过计算运行平稳性指标判定。
1.运行稳定性
(1)脱轨系数为轮对的横向力与相同轮对上的竖向力比值。理论计算脱轨系数与列车速度的关系,随速度增加先增加后减小,在100km/h出现最大值,其变化范围为0.077~0.104;现场实测脱轨系数随速度增加先增加后减小,其变化范围为0.07~0.09。同时理论值大于现场实测值,均满足我国规范规定的脱轨系数小于0.8 的要求。说明车辆运行稳定性较好,见图12。
(2)轮重减载率为静轴重减动轴重与动轴重的比值。理论计算列车的轮重减轻载率与列车速度呈线性增加,速度越大,轮重减轻载率越大,其变化范围为4.7%~10.2%,现场实测列车重减轻载率随速度增加,但影响不大,其变化范围为1.3%~1.6%。理论值大于现场实测值,均满足规范要求的轮重减轻载率小于0.6 的要求。说明车辆运行稳定性较好,见图13。

图13 车速与轮重减载率曲线Fig.13 Speed and rate of wheel load reduction
2.运行平稳性
车辆运行平稳性是评价乘车平稳性的指标,理论计算对比分析可以看出平稳性与速度大致呈现线性增加的趋势,平稳性实测值均大于理论值。竖向平稳性实测最大值为1.79,横向平稳性实测最大值为2.23,均满足规范乘车平稳性指标应小于2.5,评价为“优”。说明轨道状态与车辆运行状态匹配性较好,见图14。
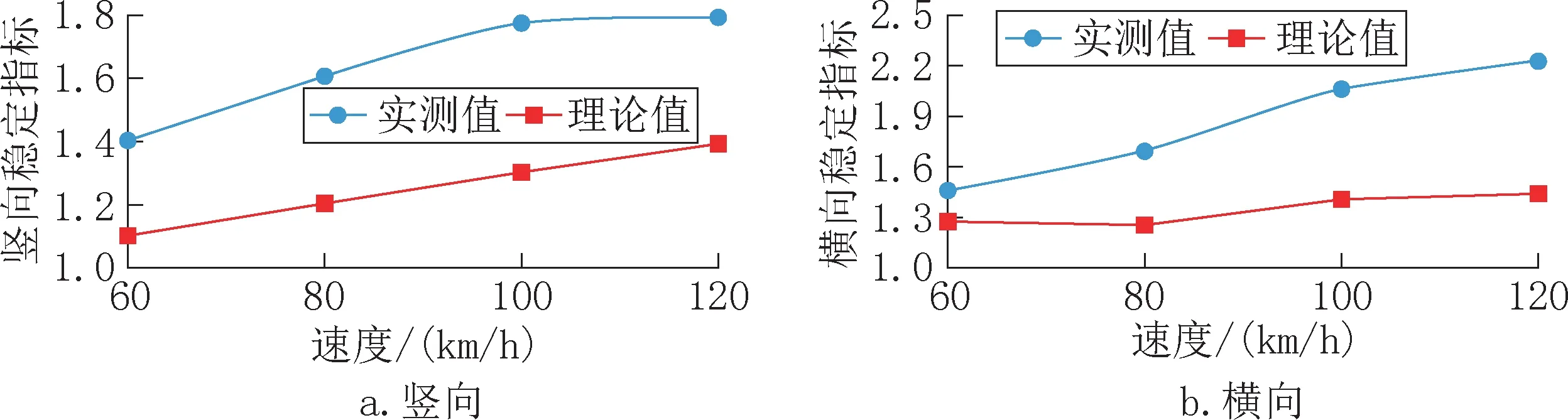
图14 车速与稳定指标曲线Fig.14 Speed and stability index
4 结论
1.低速时桥梁响应随速度增加而增长。在B型车以速度60km/h~120km/h 通过时,竖向振动位移、加速度最大值为27.955mm 和49.676mm/s2;横向响应最大值出现在100km/h对应时速下,连续梁跨中横向振动位移、加速度最大值为0.030mm、34.170mm/s2;在低速时跨中竖向动态放大系数随速度的增加而增加;在60km/h对应上述值为1.010;随速度的进一步增加该响应逐渐变小,在时速为120km/h对应上述值为1.043。
2.低速时车辆响应随速度增加而增长,在达到100km/h出现最大值,其后随速度的增加而趋于稳定。在B 型车以速度60km/h~120km/h 通过时,其最大值出现在120km/h对应时速下,车体的脱轨系数、轮重减载率、竖向和横向平稳性指标最大值分别为0.104、10.2%、1.387、1.448;在低速时上述响应随速度的增加而增加,在60km/h 对应上述值为0.077、4.7%、1.095、1.279;随速度的进一步增加该响应的变化逐渐变小,在时速为120km/h 对应上述值为0.094、10.2%、1.387、1.448。
3.理论计算数值与实测值吻合度较好,能够较为准确地反应变化趋势。同时在B型车以速度60km/h~120km/h 通过时,舒适性等级均达到“优”。

