中承式拱桥钢骨混凝土组合结构拱座分析
李兴宇 彭亚东 何维利
北京市市政工程设计研究总院有限公司 100082
引言
拱是结构也是建筑[1],拱桥由于其景观性和跨越能力,应用广泛。近年来,中国的钢-混组合结构系杆中承式拱桥发展迅速[2],该桥型主梁以上部分为钢拱肋,主梁以下部分为混凝土拱肋。这种拱桥结构充分利用了两种材料的特点,梁上钢拱肋结构较轻,便于架设施工,梁下混凝土拱肋刚度较大,处于涉水环境时,混凝土结构耐久性较好。拱座是拱桥的重要节点,承受并传递拱桥全部上部结构荷载。由于拱桥的拱座受力集中,内力很大,作为拱桥设计的控制节点,设计中需给予特别地重视[3,4]。中承式拱桥拱座需同时承担并传递主拱和边拱传来的内力,受力复杂[5],若拱脚和拱座采用混凝土结构,则常常内置劲性骨架,增强结构的强度和可靠性。受力复杂的钢骨-混凝土组合结构计算难度大[6,7],目前国内桥梁专业钢-混组合结构参考规范有《公路钢混组合桥梁设计与施工规范》(JTGT D64-01—2015)和上海市地方标准《型钢混凝土组合桥梁设计标准》(DG/TJ 08-2299—2019)规定了工字型截面的计算方法,对于异形截面来说,相关参考规范资料较少。
本文采用实体单元模型和基于平截面假定理论的平面有限元模型,对京雄高速(北京段)起点处的300m中承式拱桥的钢骨混凝土结构拱座进行了分析和评估,为该桥的拱座结构提供了设计依据。
1 工程概况
永定河大桥为京雄高速(北京段)起点处的一座特大桥,大桥跨越永定河,主桥立面如图1 所示,主桥为(60 +50 +300 +50 +60)m 的中承式提篮拱桥,主拱跨径300m,边拱跨径为50m,两侧各设置一跨60m的辅助孔。拱肋为双曲提篮拱,横向内倾角为15.64°,拱顶采用中国结式的风撑进行连接。主拱矢跨比为1/4,拱轴系数1.5,主拱为钢-混组合结构,拱肋横梁及以上范围为钢结构拱肋,主拱下拱肋、拱座和边拱为混凝土结构。主桥11#墩~14#墩范围内桥梁宽度为48m,由辅助墩(11#墩和14#墩)中线两侧各6m至过渡墩桥梁宽度由48m渐变至42m。
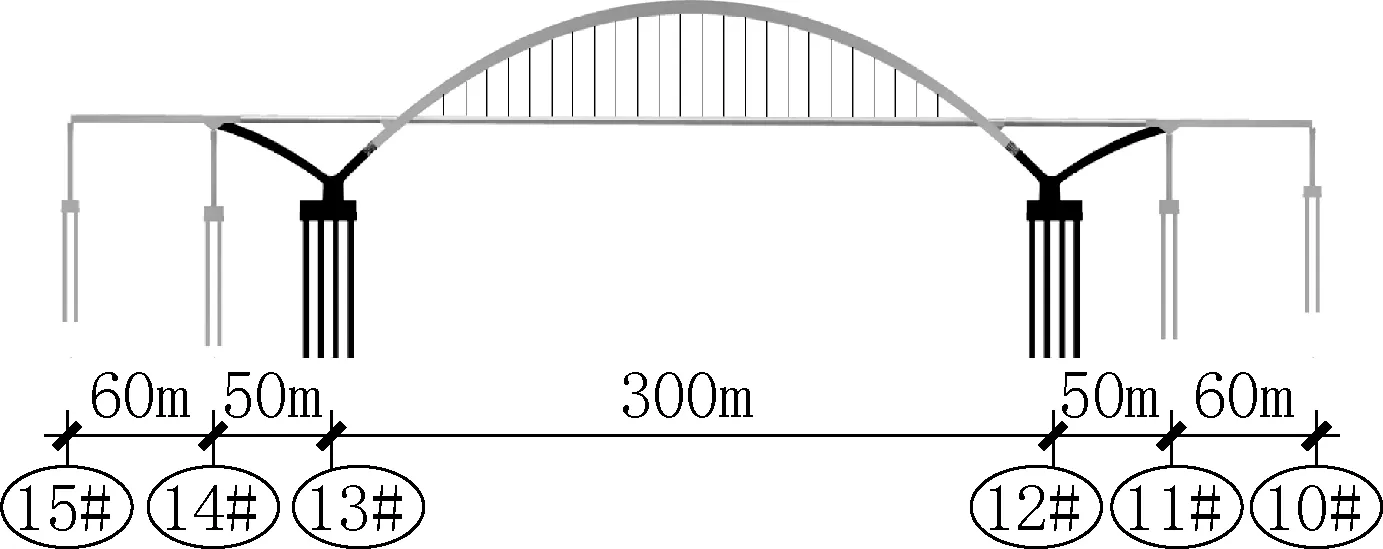
图1 京雄永定河大桥主桥立面图Fig.1 Main bridge elevation of Jingxiong Yongding river bridge
永定河大桥桥位处于地震烈度8 度区,设计加速度0.2g,下部结构设计由地震荷载控制。本桥位位于永定河与京雄高速交汇处,永定河河道限制阻水比不超过5%,因此本桥拱肋拱脚和拱座结构顺桥向尺寸设计的比较薄,拱座尺寸如图2、图3 所示,为增大拱座的顺桥向刚度和拱脚、拱座连接的可靠性,在拱座、拱脚内部设置型钢骨架。
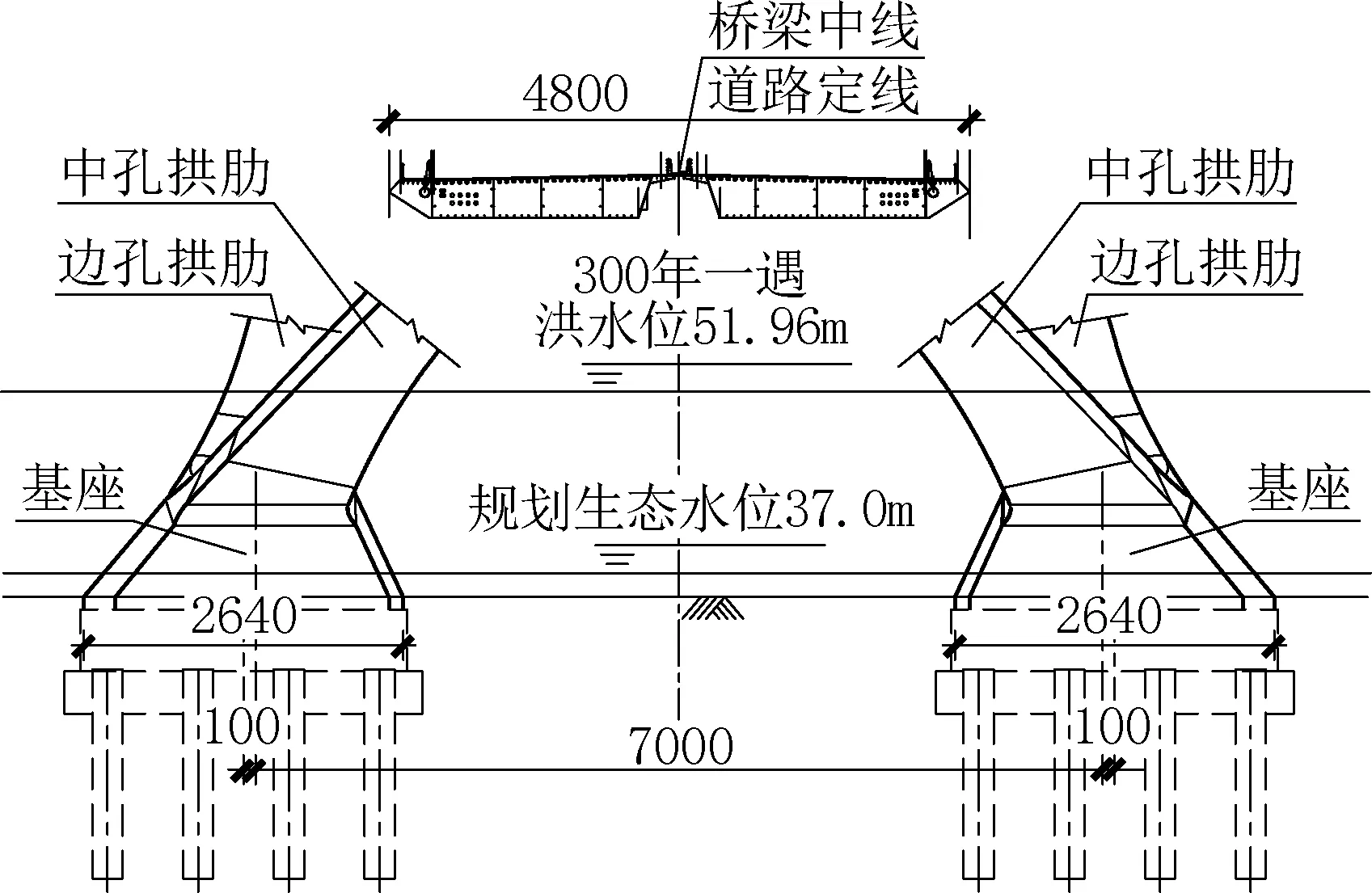
图2 主桥拱座处横断面图Fig.2 Cross section view at the arch base of the main bridge
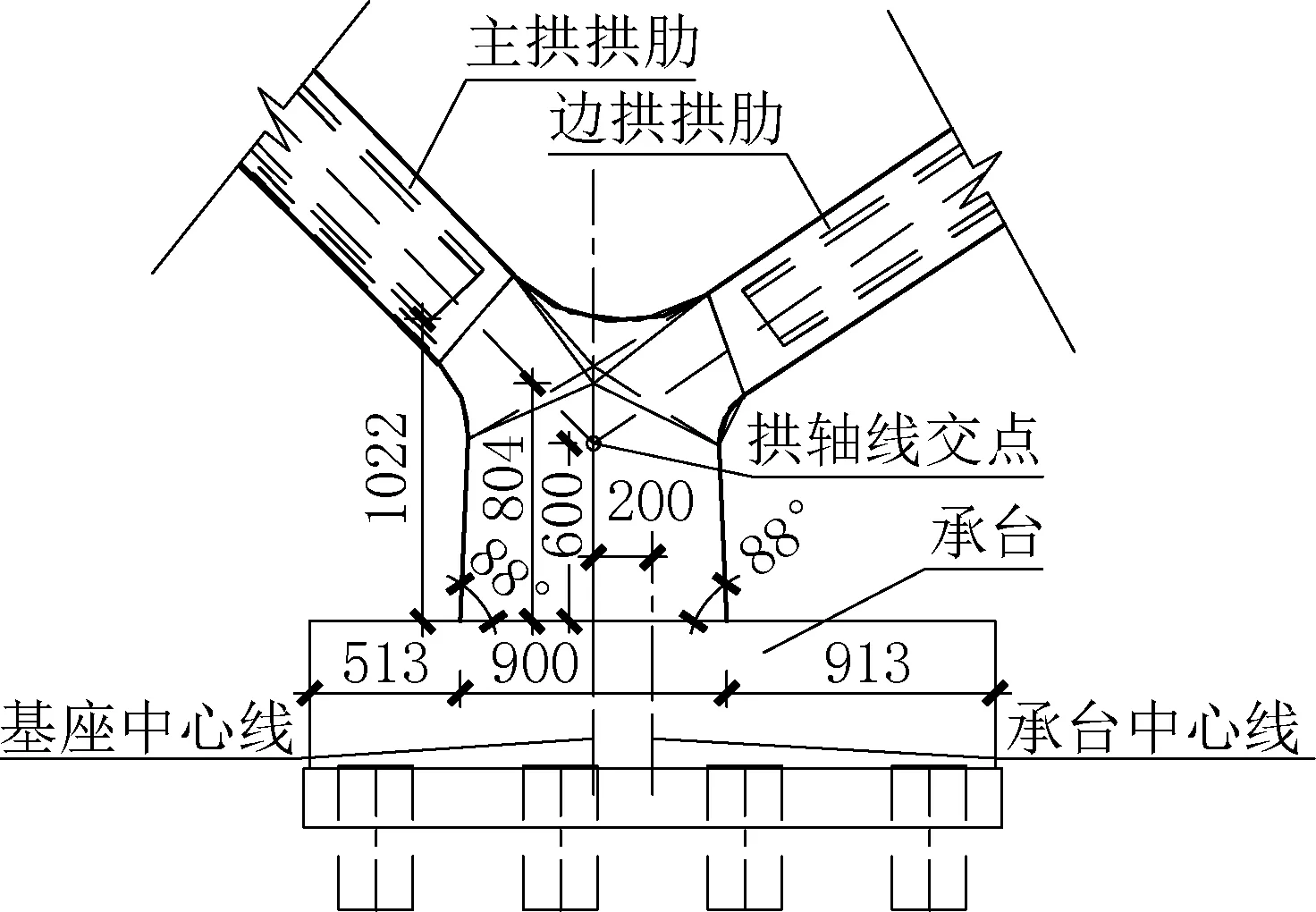
图3 主桥拱座顺桥向立面图Fig.3 Vertical view of main bridge arch along the bridge direction
2 钢骨混凝土结构拱座应力分析方法
桥梁工程设计中,通常分两步对桥梁结构进行计算分析:(1)采取梁单元对全桥结构建立杆系模型进行整体计算,从整体杆系模型中提取桥梁局部内力;(2)对桥梁局部构件用实体单元建模进行局部计算。
由于本桥拱座结构为钢筋混凝土结构内置钢骨架,由于钢筋混凝土结构受拉会开裂,为正确考虑结构内钢结构的受力状态,局部计算模型中需考虑混凝土开裂状态,通常采用混凝土弥散开裂模型进行模拟[8]。但是弥散开裂单元模型为非线性计算方法,当结构模型较大,单元较多时,计算工作量较大,对计算机配置要求较高。拱座为拱桥安全的生命线,一旦损坏维修难度大,为提高拱座安全系数,大桥拱座在地震作用下按弹性状态设计,结构分析思路:首先由实体模型验算拱座成桥状态的应力状态,判断拱座在成桥状态下的应力大小和受力是否均匀,若受力均匀则认为可以采用基于平截面假定对拱座截取控制截面建立平面有限元模型验算不同工况下拱座结构的应力[9]。若各工况下结构应力在规范允许范围内,则认为结构设计为安全的。
永定河大桥拱座设计中,钢骨混凝土组合结构拱座的分析方法:
第一步:用ABAQUS 建立实体有限元模型,对拱座成桥状态进行有限元实体模型分析。
第二步:截取拱座设计控制截面,采用Midas Civil中的“任意界面设计器”建立可考虑混凝土材料开裂的平面有限元模型,计算截面各材料(钢骨架、混凝土、钢筋)应力。
3 模型建立及内力分析
3.1 全桥空间杆系模型
用Midas Civil对全桥建立空间杆系模型(图4所示)进行计算,并提取拱座设计内力,用以进行拱座的局部应力分析。拱座主要承受主拱和边拱拱脚传递下来的荷载,拱座成桥状态的受力如图5 所示,F、Q、M分别为顺桥轴力、剪力、弯矩,横桥向弯矩和剪力图中未示。局部实体模型截取两侧拱肋距拱脚一倍拱肋高度处的截面进行内力加载。

图4 永定河大桥主桥计算模型Fig.4 Calculation model of the main bridge of Yongding river bridge
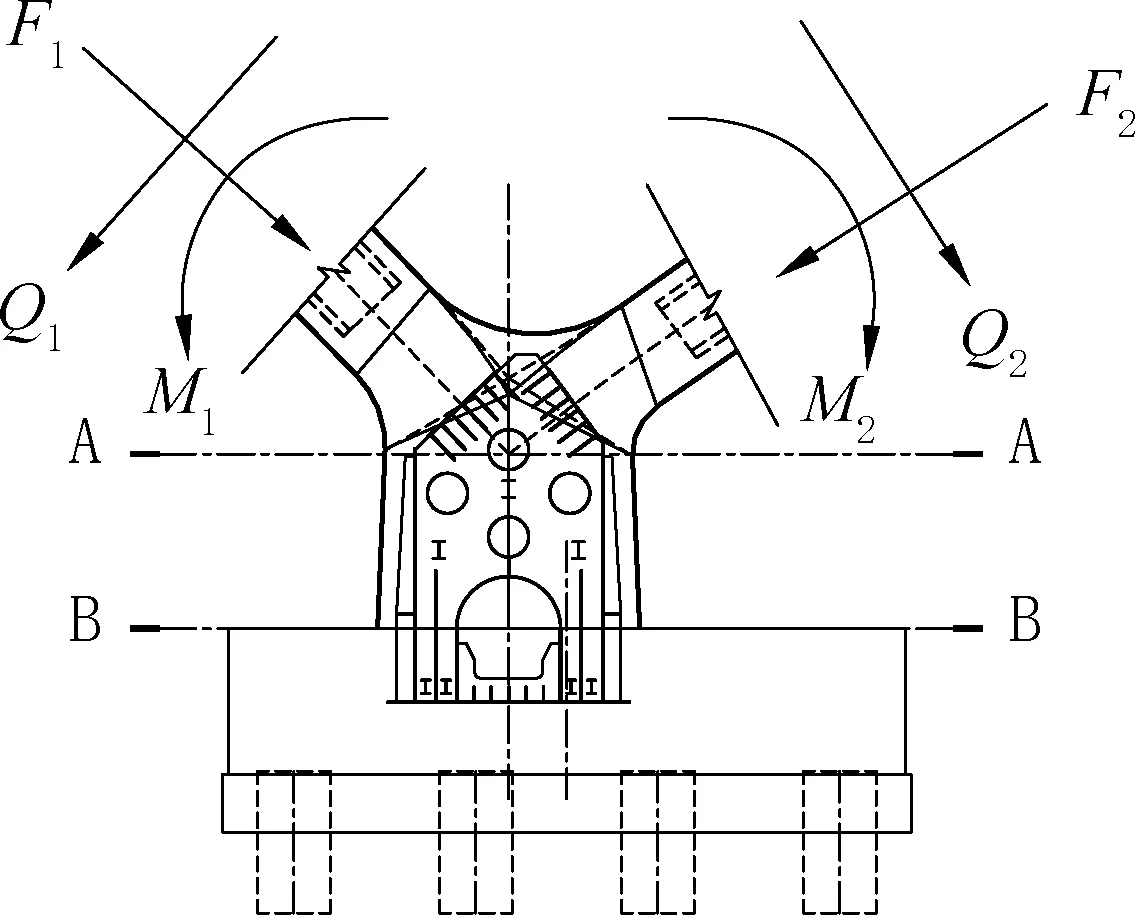
图5 拱座受力示意Fig.5 Schematic diagram of the stress on the arch seat
从Midas整体计算模型中提取成桥状态的拱脚设计内力如表1 所示。
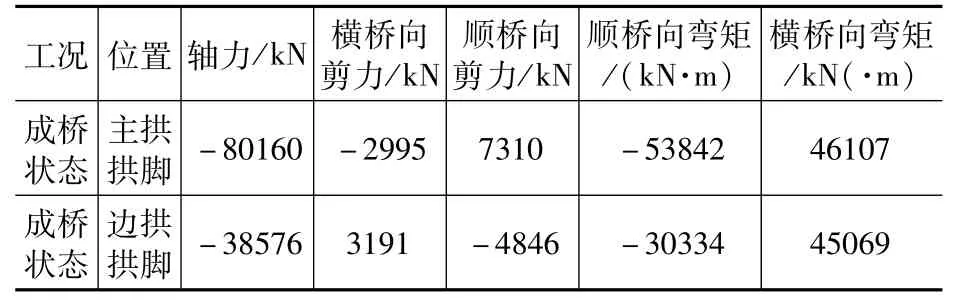
表1 成桥状态拱脚内力Tab.1 Stress of arch foot in completed bridge state
3.2 成桥状态拱座实体模型
采用ABAQUS 软件建立拱座实体模型,如图6 所示。其中混凝土采用三维实体单元模拟,钢骨架采用二维壳单元模拟,钢筋采用桁架单元模拟,钢筋与型钢骨架内置入混凝土内。

图6 拱座ABAQUS 计算模型Fig.6 ABAQUS calculation model diagram of arch
对拱座成桥状态计算得到混凝土、钢骨架和钢筋的应力结果如图7~图9 所示。

图8 成桥状态钢骨架应力(单位:N·mm)Fig.8 Steel skeleton stress in the completed bridge state(unit:N·mm)
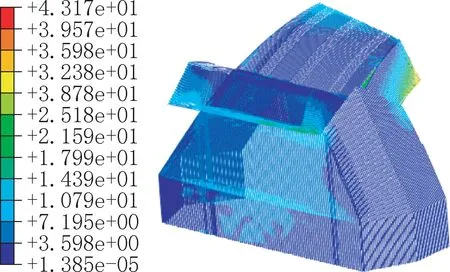
图9 成桥状态钢筋应力(单位:N·mm)Fig.9 Steel bar stress in the completed bridge state(unit:N·mm)
由图7~图9 可知:1)拱座成桥状态混凝土最大主拉应力为1.31MPa,出现在主拱侧实心段端部,拱座顶拱脚处最大主拉应力为1.0~1.3MPa,均小于拱座材料拟采用的C55 混凝土拉应力设计值1.89MPa,在成桥状态拱座混凝土未开裂;2)拱座成桥状态混凝土最大主压应力为7.66MPa,出现在主拱拱脚下缘,小于C55 混凝土压应力设计值24.4MPa,满足规范要求;3)成桥状态拱座整体应力较为均匀,无明显应力分配不均现象,且拱脚处应力分布形态基本符合平截面假定的截面应力分布状态;4)在成桥状态,拱座的钢骨架和钢筋应力状态均较小。
3.3 拱座截面验算
普通钢筋混凝土构件截面的验算只需参考规范即可,本桥拱座和混凝土拱肋为钢筋混凝土内置钢骨架结构,先行规范算法无法考虑钢骨架对结构的作用。为考虑钢骨架对截面受力特性的影响,以实体模型计算结论为依据,对拱座截取如图5 所示的A-A、B-B 截面进行验算,本部分采用Midas Civil的“任意截面设计器”建立考虑受拉区混凝土开裂的平面有限元模型进行计算。根据混凝土结构规范规定,对于钢筋混凝土结构应分别验算结构的承载能力极限状态和正常使用极限状态,承载能力极限状态主要验算构件的强度,正常使用极限状态主要验算混凝土截面的裂缝宽度。本文分别取E2 地震作用下[10]最大顺桥向弯矩工况和频遇组合最大顺桥向弯矩工况为例来介绍本文的计算方法。
在整体计算模型中提取不同工况下拱座与承台交界面(图5 中B-B)计算的内力如表2 所示。
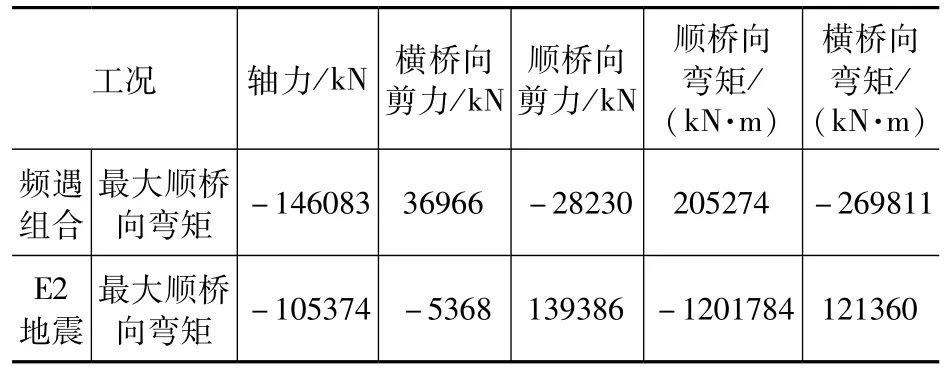
表2 拱座底截面设计内力Tab.2 Design stress of base bottom section
用Midas Civil的“任意截面设计器”建立验算截面的平面有限元模型,混凝土材料为C55,钢筋采用HRB400,钢骨架材料为Q345qE。计算模型考虑受拉区混凝土开裂。
1.承载能力极限状态验算
将表2 中E2 最大顺桥向弯矩的内力组合输入到模型中,计算得出拱座底截面的轴力-弯矩曲线如图10 所示,得出截面混凝土最大压应力7.92MPa、钢骨架最大拉应力106.8MPa、普通钢筋的最大拉应力123.7MPa,因此可以判断在E2地震作用下,拱座强度满足规范要求。
2.正常使用极限状态验算
正常使用极限状态参考《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)6.4.3 条[11],验算拱座截面在使用阶段的裂缝宽度。设计内力取验算截面的频遇组合内力和准永久组合内力,钢筋应力σss采用Midas的“任意截面设计器”进行计算。通过模型计算可得频遇组合工况钢筋应力σss=1.716MPa,代入公式得裂缝宽度为0.024mm,符合规范要求。
4 结论
本文对京雄永定河大桥的钢骨混凝土组合结构拱座进行了分析验算,具体结论如下:
1.实体模型计算结果表明成桥状态拱座的混凝土未开裂,钢骨架和钢筋受力较小,拱座结构受力均匀。
2.E2 地震作用下组合工况拱座截面验算得出拱座混凝土最大压应力7.92MPa、钢骨架最大拉应力106.8MPa、普通钢筋的最大拉应力123.7MPa,承载能力极限状态符合规范要求。
3.通过平面有限元方法计算得频遇组合钢筋应力,得到拱座正常使用极限状态裂缝宽度为0.024mm,符合规范要求。

