基于振动信号瞬时分量抽取的偏心故障特征提取方法
段晨东, 郑天添, 代杰
(长安大学 电子与控制工程学院,陕西 西安 710064)
0 引 言
感应电机在工业生产中被广泛的使用,有着不可替代的地位。电机在发生故障时,其振动信号包含了故障特征[1],可以用来监控其运行状态。采用信号处理方法从振动信号中提取出反映故障类型及严重程度的特征信息,对故障进行准确识别和分类具有重要的理论意义。偏心故障是电机常见的故障之一,故障发生时电机气隙磁场发生畸变,损坏性能参数指标甚至会烧毁设备乃至发生机毁人亡的重大安全事故。因此对电机偏心进行故障诊断研究具有实际价值。
文献[2]提出了一种基于峭度、小波降噪和共振解调法相结合的故障诊断方法,先通过峭度统计对点击运行状态进行诊断,若发生故障则通过小波降噪和共振解调法提取相应故障信号的频域信息,但此方法对信号的丢失率较高。文献[3]先推导了电机偏心故障状态下和气隙偏心与匝间短路复合故障状态下的电磁转矩表达式,并以此为依据建立了电磁转矩特征频率幅值和短路位置的一一映射关系,对电机偏心故障与匝间短路的实际监测与识别具有参考价值。文献[4]对发电机气隙静态偏心前后的电磁转矩特征进行了分析,结果表明气隙静偏心将引发电磁转矩产生二倍频波动,且随着偏心程度的加剧而更加明显,丰富了气隙静偏心故障的诊断判据。
针对偏心故障引起振动信号的异常,在短时傅里叶变换(short-time Fouriver transform, STFT)基础上提出一种瞬时分量抽取(transient-extracting transform ,TET)方法[5]371,可以去除大部分模糊的时频能量,通过对信号的处理与重构,突出了信号中的偏心故障特征频率,以此对故障进行检测。试验结果表明该方法可以准确提取出偏心特征频率,提高故障识别能力。
1 转子偏心故障
电机气隙偏心是一种定、转子间气隙空间分布不均匀的现象。如图1所示,发生偏心故障时,旋转轴与定子几何轴偏离,它们之间的偏移量为δ。在静偏心情况下,最小径向气隙长度的位置在空间中是固定的,偏移量δ不会改变;在动偏心情况下,最小径向气隙长度的位置在空间中是改变的,偏移量δ随着旋转而改变。

图1 电机偏心原理图
气隙偏心使磁导变化,引起电感和气隙磁通密度的改变,进一步导致电机内磁场发生畸变。气隙磁场分布不均匀,引起径向和轴向的不平衡磁拉力,其中的径向磁拉力作用于电机的定子和转子使电机产生振动[6]。图2为电机定子和转子偏心故障坐标系,其中:α为气隙周向角;δs为相对静偏心值;δd为相对动偏心值。

图2 电机气隙长度示意图
当发生偏心故障时,电机的气隙长度:
g(α,t)=g[1-δscosα-δdcos(2πfrt-α)]
(1)
式中:g为平均气隙;fr为电机转频。
气隙磁导与气隙长度成反比,即:
(2)
式中:μ0为真空磁导率。
一般情况下偏心量很小,将式(2)的气隙磁导展开为傅里叶级数,取前两项可得:
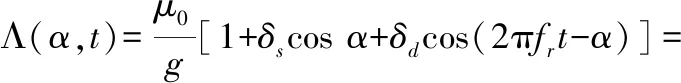
(3)
式中:Λ0为气隙磁导常量分值;Λs为静偏心引起的磁导分量,Λs=Λ0δs;Λd为动偏心引起的磁导分量,Λd=Λ0δd。对于对称三相绕组,其合成磁动势f(α,t)是一个正弦分布、以同步转速向前推进的旋转磁动势波,可表示为:
(4)
式中:fs为电源频率;kω1为绕组的基波绕组因数;N为一相绕组的总串联匝数;p为电机极对数;Iφ为定子电流有效值;β为滞后角度;F1为电机三相绕组基波合成磁动势的幅值。
根据麦克斯韦定律,发生偏心故障时单位面积的磁拉力q(α,t)为:
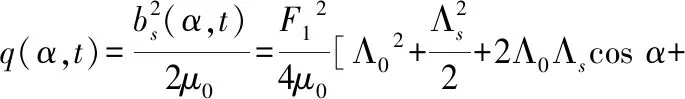
(5)
其中,气隙磁密bs(α,t)为:
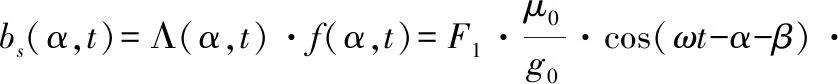
(6)
由式(5)可得由于故障导致气隙径向磁拉力引起电机异常振动故障特征频率分量分别为:fr、2fs、2fs±fr、2fs+fr、2fs-fr。
受到基波、定子和转子磁动势谐波、定子和转子槽磁导谐波以及气隙偏心磁导谐波等影响,偏心故障时它们作用在铁芯上产生的磁拉力也会引起电机异常振动。振动信号包含这些信号及其谐波分量如式(7)所示[7]。
(7)
式中:i为任意整数;ke为动偏心系数,静偏心时为0,动偏心时为较低的整数;n=0或任意整数;Nr为转子导槽数。
另外,由于出现匝间、线圈间、相间或相间接地,导致定子绕组故障[8]。正常情况下,定子所受单位面积磁拉力的合力为0,当电机发生匝间短路时,气隙磁密发生改变导致气隙磁场的不均匀,引起不平衡磁拉力引起异常振动。在低频部分也会出现倍频电源频率2fs,在高频部分会出现Nrfr±2fs、Nrfr±4fs等分量[9]。
2 TET瞬时分量抽取方法
STFT等分析方法较好地揭示了信号的时频特征,但是其无法精准对时频信息定位。为了有效提取故障信号中暂态分量,增强对信号信息的定位能力,将狄拉克(Dirac)函数与STFT方法相结合,提出TET方法[5]372。
设s(t)的短时傅里叶变换为:

(8)
式中:g(·)为窗函数。
在t0时刻,Dirac函数可表示为s(t)=A·δ(t-t0),代入式(8)变为:

(9)
由于|e-iωt0|=1,则式(9)的能量分布为:
|G(t,ω)|=A·g(t0-t)
(10)
由式(10)可以很容易看出能量集中分布在t0这一时刻。但由于窗函数的影响,时频的能量分布在[t0-Δ,t0+Δ],其中Δ为窗函数时间。
Dirac函数的短时傅里叶变换是由一系列具有相同群延迟时间t0的Dirac函数构成的,为了计算群延时时间t0,对式(9)求导,可得:
(11)
为了使能量不受群延时能量分散的影响,定义了瞬态提取算子(transient-extraction operator, TEO)为:
TEO(t,ω)=δ[t-t0(t,ω)]
(12)
考虑到群延时时间t0(t,ω)为:
(13)
可得到δ[t-t0(t,ω)]=δ(t-t0),即TEO算子只在t0处有有效值,在其他地方为0。通过TEO算子提取的STFT变换瞬时分量为:
Te(t,ω)=G(t,ω)·TEO(t,ω)
(14)
同时因为Dirac函数具有如下性质:
f(x)·δ(x-x0)=f(x0)·δ(x-x0)
(15)
因此新的时频分布可表示为:
|Te(t,ω)|=|G(t,ω)·TEO(t,ω)|=
|A·g(t0-t)·e-iωt0·δ[t-t0(t,ω)]|=
|A·g(t0-t)·e-iωt0·δ(t-t0)|=
A·g(0)·δ(t-t0)
(16)
相较于对信号的STFT结果[式(8)],改进后的方法[式(16)],使频谱得到集中,并且仅出现t0时刻,对信号的信息提取能力得到显著提升。
3 工程应用
试验数据来自于电机故障模拟试验台[10],试验电机为YE2-100L2-4,额定电压380 V,额定电流6.8 A,额定功率3 kW,额定转速1 420 r/min(23.67 Hz),有28个转子导槽,36个定子导槽和4对磁极。
通过在转子端部粘贴两个螺帽以增加额外质量使定子转子间气隙变化,以模拟偏心故障。传感器在机壳上采集轴向振动信号,采样频率为10 kHz。图3为一组偏心振动信号,电机的实测转速为1 497 r/min(24.95 Hz),长度为8 192。

图3 振动信号及其频谱和包络谱
图3(a)为振动信号波形,图3(b)、图(c)为其频谱和包络谱。在图3(b)可以看到转频fr、电源频率fs、转频与电源频之和fr+fs,以及转条通过频率与电源频率的偏移Nrfr±fs(748.29 Hz、848.39 Hz)、Nrfr±2fs(689.41 Hz、948.48 Hz)等。在图3(c)包络谱中不能观察到明显的低频成分,高频中可以看出部分与转条相关的偏心故障频率fecc(623.78 Hz、823.97 Hz)。
对信号进行时频分析,结果如图4所示。
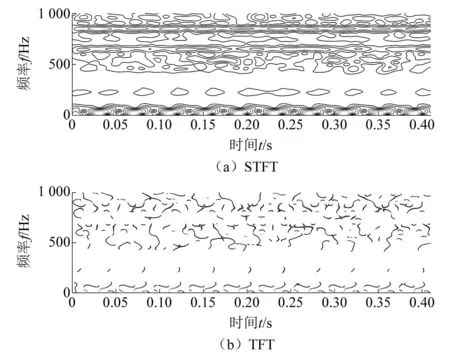
图4 STFT和TET分析结果
可以看出,图4(a)的STFT结果提供了模糊的瞬态信号,不能通过时频信息对信号的精准定位。图4(b)TET结果中频率信息相较于STFT结果更加明显,信号得到集中。
重构信号与其包络谱如图5所示。
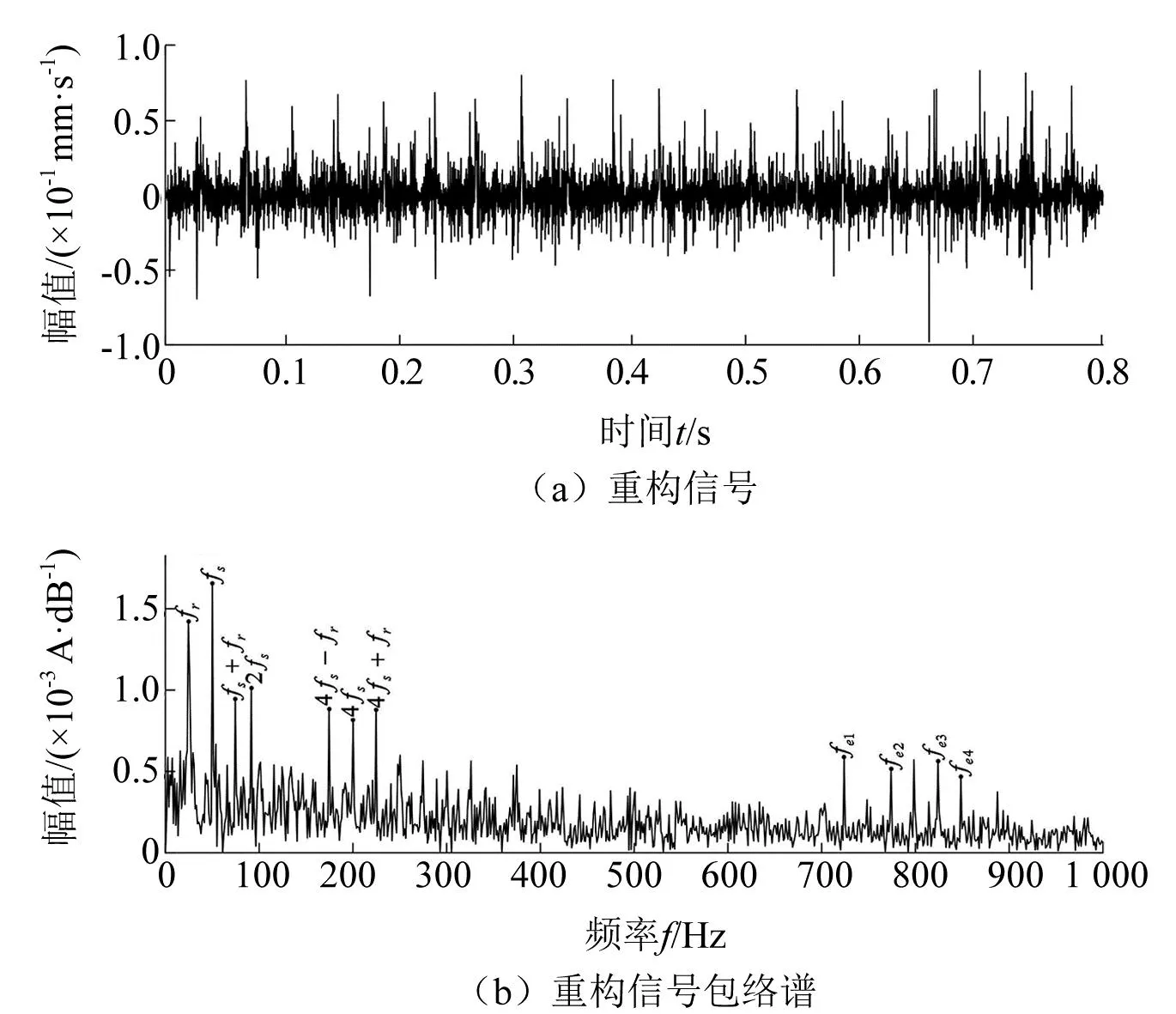
图5 重构信号及其重构信号包络谱
如图5(a)所示,与原始信号相比,重构信号瞬态特诊得到改善,能反映出故障冲击成分。对重构后的信号进行包络谱分析,可以从图5(b)看出有关于气隙偏心低频部分的特征频率2fs、2fs+fr、2fs-fr及高频部分偏心故障频率fecc(fe1723.78 Hz、fe2773.92 Hz、fe3823.97 Hz、fe4848.39 Hz)等。相较于对原信号的包络谱结果,对重构信号提取包络可以提取出明显的特征幅值。结果表明,通过TET方法对信号进行抽取与重构,对重构信号包络谱处理提取转子偏心故障特征频率,可以识别出偏心故障。
图6(a)为一组2圈匝间短路的故障信号,试验将相邻两匝定子线圈短接,数据的采样频率为10 kHz,长度为8 192。

图6 原始振动信号及其信号频谱和包络谱
图6(a)为原始振动信号波形,图6(b)、图6(c)为其频谱和包络谱。从图6(b)频谱结果中不能观察到低频部分,但可以看到Nrfr±fs(748.19 Hz、848.38 Hz)、Nrfr±3fs(648.19 Hz、948.49 Hz)等高频特征幅值。图6(c)包络谱中可以看出转频fr、电源倍频2fs、4fs等低频信息。
利用TET方法对信号进行时频分析,结果如图7所示。
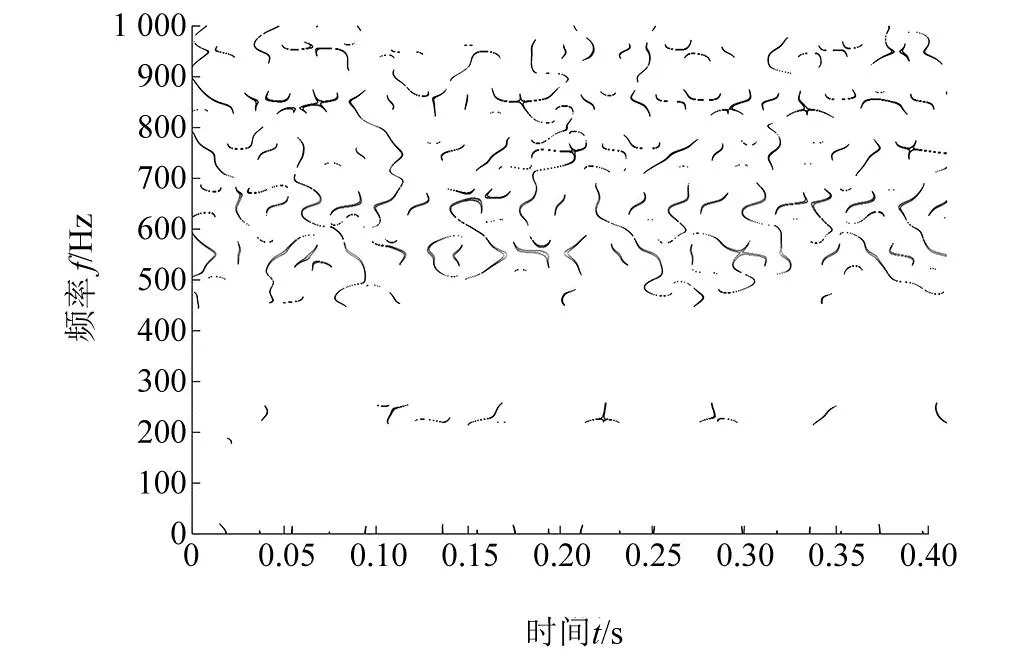
图7 TET结果
从图7可知,TET能够将信号集中表示,在500~600 Hz、600~700 Hz、700~800 Hz和800~900 Hz等频带可以观察到明显的时频信息。
本文提取TET结果中的瞬态分量对信号进行重构,并对其进行包络谱分析,结果如图8所示。
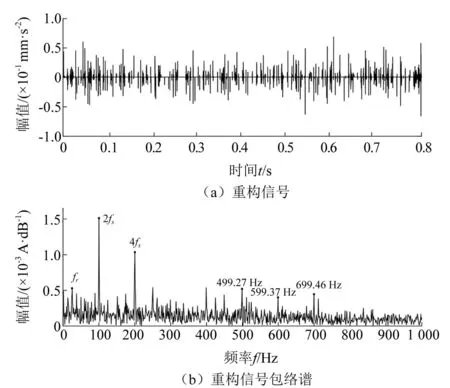
图8 (a)重构信号 (b)重构信号包络谱
从图8(a)可以看出,重构信号保留了匝间短路所导致不均匀磁场的重复冲击成分。图8(b)因匝间短路所引起的偏心故障特征转速频率fr、电源倍频2fs、4fs相较于处理前的结果,幅值提升。由于故障径向异常振动所导致的特征频率Nrfr-2fs(699.46 Hz)、Nrfr-4fs(599.37 Hz)等也能被提取出来,从包络谱中得到的故障频率具有清晰的特征。结果表明,匝间短路也会引起气隙磁场的不均匀,导致异常振动,在低频部分具有和气隙偏心一样的特征频率。
4 结束语
本文以三相异步电机振动信号为研究对象,与时频TET方法相结合,对电机的气隙偏心故障与匝间短路进行诊断识别。该方法利用Dirac函数优异的时间定位能力,对STFT进行改进,去除大部分模糊的TF能量,剩下与信号密切相关的时频信息,保留了的瞬态特征。分析实际数据表明,时频信号得到集中,重构信号保留了原有的故障特征频率,能有效提取出故障频率。除气隙偏心故障外,匝间短路所引起的偏心故障频率也可以正确提取,能够识别出故障类型,在电机的偏心故障诊断中具有很大的应用前景。

