基于粒子群算法的直流配电网电压波动研究及算例分析

祝亚峰, 吴俊, 裴春明, 韩明, 张璐, 王启明, 李峰

(1.国网电力科学研究院武汉南瑞有限责任公司,湖北 武汉 430000; 2.宜宾远能电业集团有限责任公司,四川 宜宾 644000;3.武汉理工大学 机电工程学院,湖北 武汉 430070)

0 引 言

直流配电网通常呈现多源多变换特点,具备自身独特的电能输送控制特点,而且提高敏感负荷比例后,还需电网系统达到更高电能质量水平[1-3］。为了对电能质量开展高效分析,应在直流配电网中加入专门的电能质量监测系统,实现扰动信号的精确判断,再通过分析扰动特征参数来设计优化处理方案以实现改善电能质量的效果[4-5］。

采用直流配用电技术进行处理时无需分析相位、频率等多种因素造成的影响,在船舶结构设计以及航空部件、精密控件领域发挥了重要作用,但到目前位置还很少有文献报道将其应用到大规模直流配电领域[6］。当前,大部分学者主要从系统故障、拓扑分析以及系统运行控制层面开展相关研究工作,尚未针对电能质量优化开展更加深入的探讨[7］。其中,有文献探讨了电能质量与电压波动程度之间的关系并构建了合适的治理方案,再以交流系统评价指标建立了可以高效评价直流电能质量的判断模型,但这些研究工作并未进行直流电能质量扰动的辨识分析[8］。考虑到实际交直流系统呈现不同的电能质量变化特征,因此无法将传统交流电能质量分析模式直接移接至直流系统,需重新开发一种可以准确分析直流电能质量扰动的新技术。

1 直流电能质量分析

1.1 直流电压偏差

以相对额定电压更高与更低两种条件设置两种直流电压偏差,当偏差超出允许区间后,则认为存在过电压或出现欠电压的状态,因此可以根据电压偏差程度进行判断。

在直流配电网中如果有电流经过配电系统内阻时将会产生压降,从而在线路中产生恒定的电压差,计算式如式(1)所示。

(1)

式中:ΔU为直流压降;Rs为配电系统内阻;P为系统有功功率;UN为电压偏差值。

调整直流配电网参数后,将会产生特定形式的潮流分布,从而引起母线电压偏移的现象。从图1可以看到当直流配电网受到电压偏差影响时发生的波形变化。

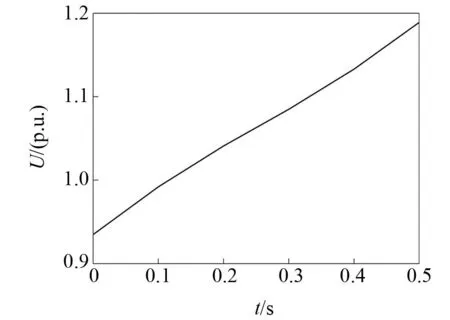
图1 电压偏差

1.2 直流电压波动

直流电压呈现明显的无规则变化特点,可以观察到明显的连续快速变化,同时变化幅值都未超过10%。由于直流配电网中存在多种形式的接入端,可根据直流母线构建得到的电容表达式求解接入端中功率的交换状态。

当设置不同的储能和负荷后或在交流部分形成不同的电网功率情况下都会造成直流母线有功功率发生明显波动,由此形成了波动变化的直流母线电压。从图2可以看到直流母线的电压波动趋势。

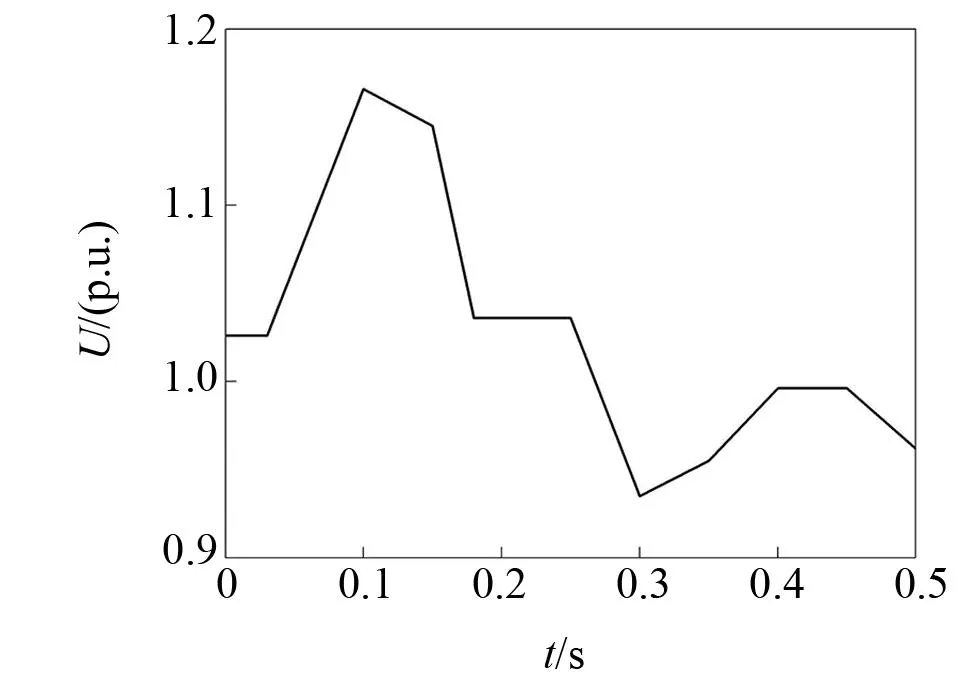
图2 电压波动

通常需要不同因素相互作用情况下才会形成电压纹波。如果在配电网中形成非对称形态的交流负荷时便会导致直流母线内产生二次纹波,同时也可以利用变流器对交流电网n次谐波实施转变处理使直流侧产生n+1次的纹波,随着开关函数的变化,将会引起变流器在直流侧产生基波和高频纹波。随着直流母线中产生多源纹波后,相互出现叠加的结果,对电能质量会造成明显损害。同时发现,电压纹波受到纹波注入源的作用后形成了明显差异性,在大小与作用时间方面呈现显著波动性,最后还会产生独特的交流分量。考虑到整数纹波是对直流电能质量的最关键影响因素,在本文中只开展整数纹波的探讨。

2 基于粒子群算法优化的支持向量机分类器 设计

支持向量机根据统计学原理开展机器学习,可以实现小样本的快速学习过程,该方法也可以被应用到具有非线性变化特征的直流电能扰动。粒子群算法的迭代表达式如式(2)所示。

(2)

式中:Vid为飞行速度;xid为飞行位置;k为迭代次数;d为维度;C1、C2为学习因子;r1、r2为随机数;ω为惯性权重。

经交叉测试后实现准确分类,由此构建得到粒子群算法适应度函数Fz,计算式如式(3)所示。

(3)

式中:s为分类数;l为验证集样本数;lt为验证集正确样本数。

图3给出了粒子群算法优化的算法流程。

图3 粒子群算法流程

3 算例分析

本文构建了呈对称单极辐射形态的直流配电网模型。图4给出了此模型的组成部分,具体参数见表1,按照6.4 kHz的恒定频率实施采样。

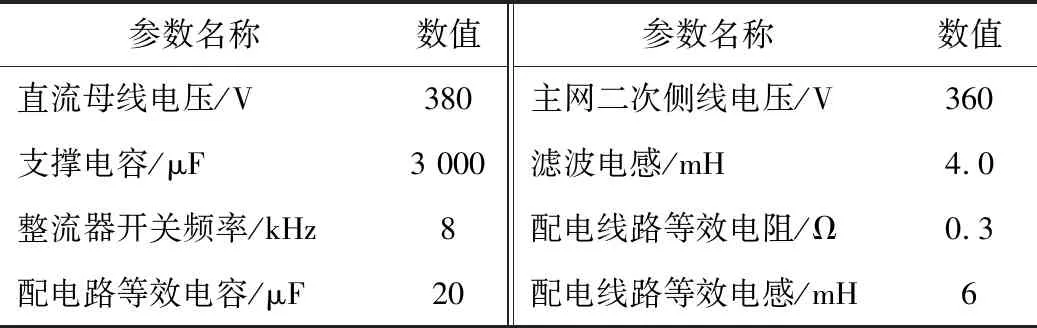
表1 配电系统参数

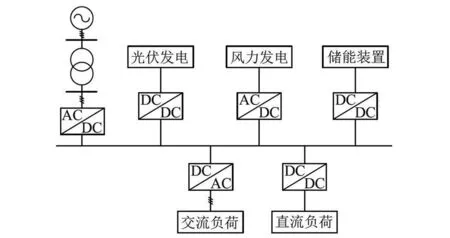
图4 直流配电网结构

根据以上机理依次开展电压偏差、参数波动、纹波形态与故障暂降的仿真测试,共获得150组扰动样本,产生了30条扰动数据。按照图5的流程框架对各项数据实施处理,最后形成了表2中的电能质量特征。

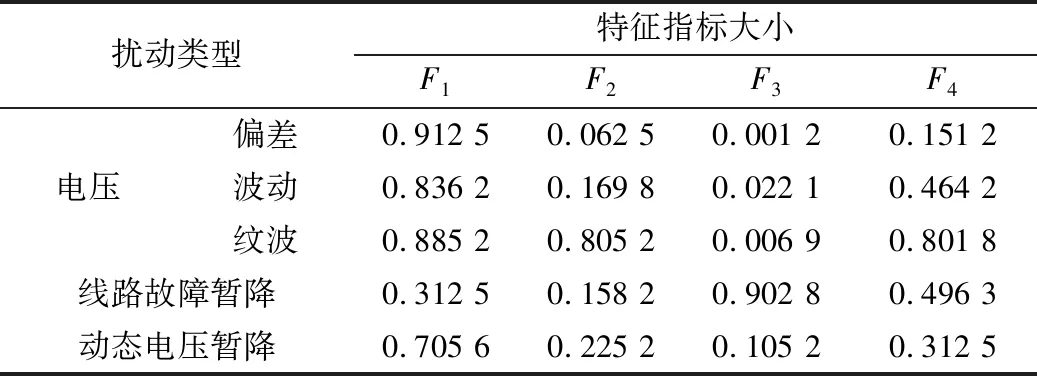
表2 特征向量

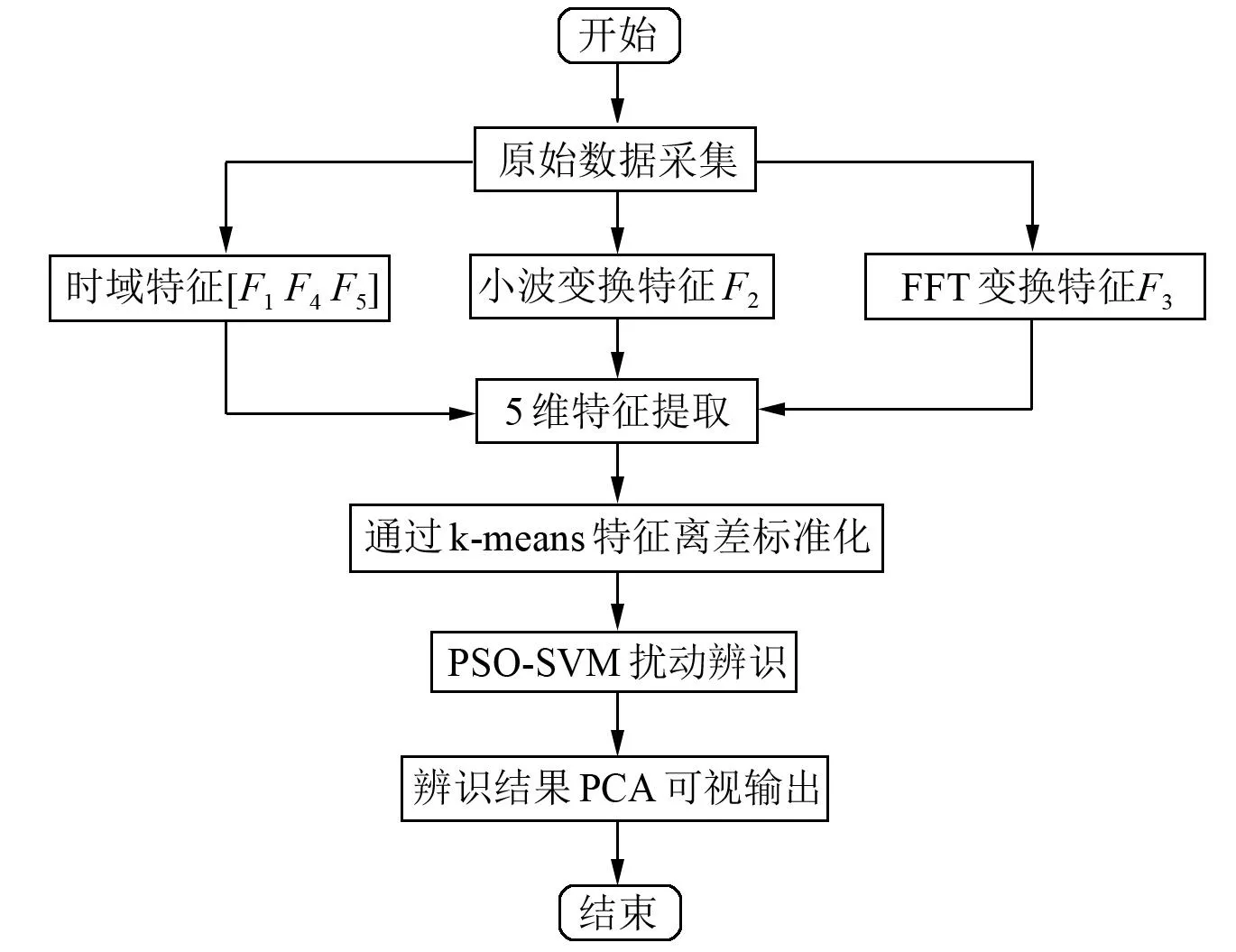
图5 数据处理

按照k-means聚类的方式总共测试了100条样本参数,形成了图6的轮廓系数变化趋势。结果发现,每种类簇下的轮廓系数都接近1,此时可选择特征集方法来准确分析直流电能质量的扰动形态。

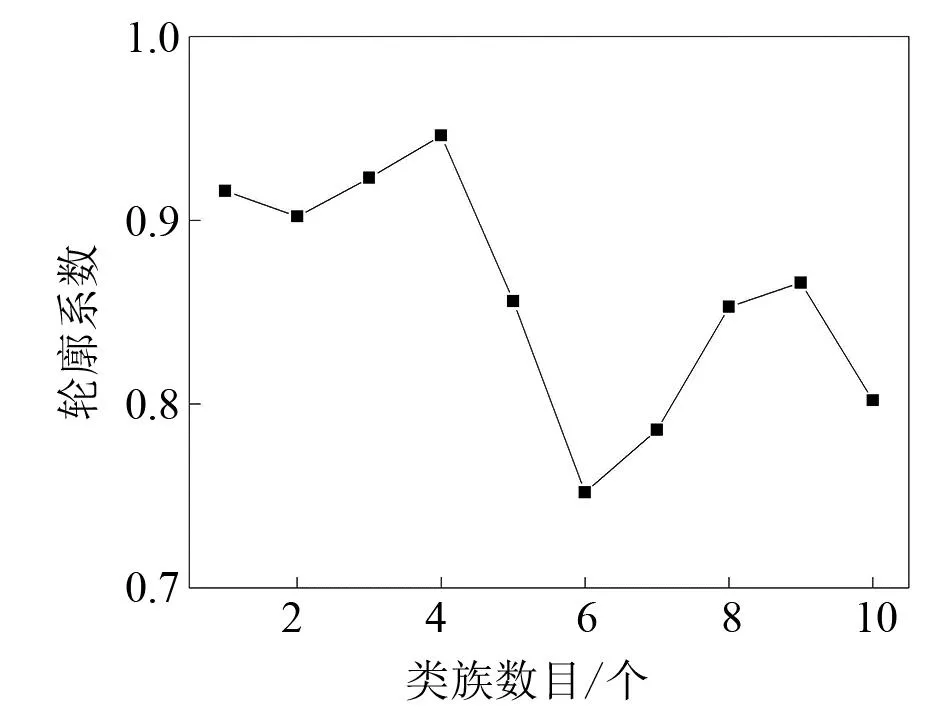
图6 轮廓系数变化趋势

建立分类器再对样本实施训练与测试,同时以表3的参数对样本实施分配。图7给出了对参数优化样本开展测试所得的结果。经测试可知,共28个样本达到了正确分类的状态,其中,电压波动与电压纹波都只出现了一类错误结果。对少数样本实施训练时,准确率可以达到92.3%以上。

表3 各类样本统计 单位:个

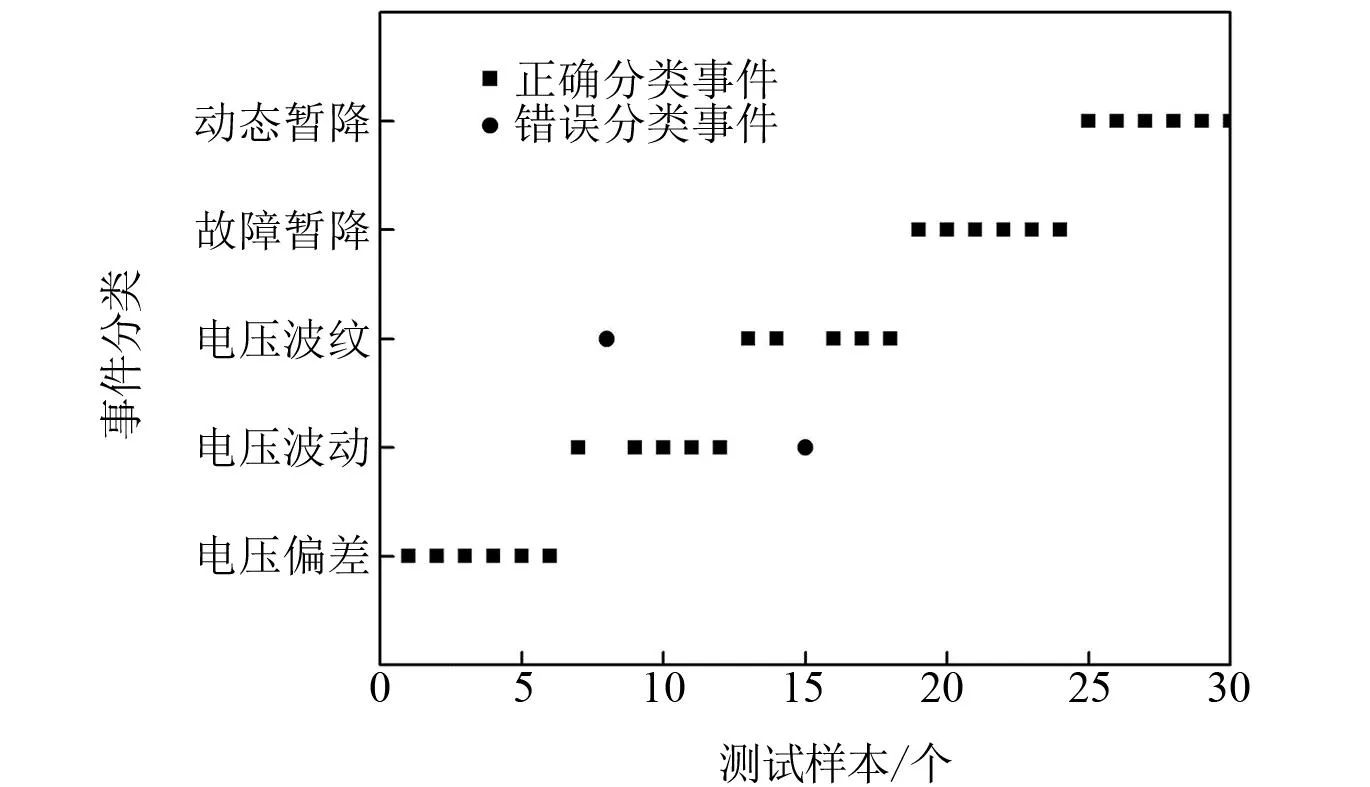
图7 测试样本分类结果

为比较各类方法进行分类的性能,本文共选出了150组样本开展测试,并将结果列于表4。分析表4可以发现,以BP神经网络算法处理时,分类准确率出现了显著下降,与支持向量机算法相比需提供更多数量的训练样本。造成这一结果的原因是以最低经验风险建立的神经网络算法对于特定数量样本条件无法实现期望风险的有效控制。而以最低结构风险构建的支持向量机算法则可以防止产生局部极值的缺陷,实现准确率的明显提升,因此以支持向量机算法进行处理时更适合小样本数据的扰动性能分析。

表4 多组模型对比结果

综合考虑本文算法以及多分类支持向量机算法各自特点可以发现,以本文算法进行处理时可以实现准确率的进一步提升,从而优化粒子群算法数据处理性能,但需要比多分类支持向量机占用更长处理时间,这是由于在参数优化期间所需的时间明显增加,而模型训练则是按照离线形式进行,不会造成最终测试时间的明显变化。

4 结束语

(1) 每种类簇下的轮廓系数都接近1,此时可选择特征集方法来准确分析直流电能质量的扰动形态。对少数样本实施训练时,准确率可以达到92.3%以上。

(2) 以支持向量机算法则可以防止产生局部极值的缺陷,实现准确率的明显提升,更适合小样本数据的扰动性能分析。以本文算法进行处理时可以实现准确率的进一步提升,从而优化粒子群算法数据处理性能,但需要比多分类支持向量机占用更长处理时间。