基于负荷分类的紧急减负荷控制多目标优化方法
李雯鑫, 赵启, 张路, 彭寅章,2, 高兴, 杨帅
(1.国网新疆电力有限公司 电力科学研究院,新疆 乌鲁木齐 830013;2.新疆大学 电气工程学院,新疆 乌鲁木齐 830047)
0 引 言
随着智能电网的发展,能源互联网地双向推进,负荷分类管理成为可能[1-2]。同时,特高压直流输电规模的阶跃式提升,对故障后紧急负荷控制协调决策提出更高要求[3-4]。根据电力行业事故处理相关规定条文,电力生产企业需同时承担系统切负荷造成的负荷损失以及事故罚款,还应考虑系统电压稳定性[5-6]。综上所述,在实现紧急减负荷控制措施时,应综合考虑技术导则的规定和减负荷控制策略的经济代价,采用多目标算法对控制策略进行寻优[7]。
文献[8]设计了以牺牲经济性的切负荷控制和电压薄弱节点集跌落量加权和最小为目标的方案,应用原对偶内点法求解控制策略。文献[9]建立可中断负荷切除总量、切除负荷个体总数的多目标调度模型,采用线性加权因子通过贡献度计算目标函数指标,提高了运算速率但同时也限制了解集的多样性。文献[10]以减负荷的经济代价和减负荷率的加权和为目标,通过平衡减负荷率的方法实现分散切负荷,而这种切负荷的方法并不能满足经济性的要求。
现有紧急负荷控制方案在协调经济性能和系统性能的多目标求解方面,以及智能电网背景下负荷的分类控制方面还缺乏更全面的研究。本文提出了一种考虑负荷分类的协调经济性及系统稳定性的多目标优化方法,建立以补偿金额、惩罚金额和电压稳定为目标的多目标调度模型,改进传统带精英策略的非支配排序遗传算法(elitist non-dominated sorting genetic algorithm,NSGA-Ⅱ),优化了结果分布,缩短了运算时间并保证了最优解集。
1 紧急减负荷问题的数学模型
1.1 柔性负荷分类策略
对柔性负荷细分类,根据负荷参与调度的难易程度不同采取不同的补偿措施可有效提高经济效益[11]。设Ⅰ类负荷为可转移也可中断型负荷,例如冷储凝空调,有一定储存能量的功能,用电时段敏感度低易调控且补偿费用低廉,实际操作中优先切除。Ⅱ类负荷不可转移可间歇性中断,如电暖气等设备,短时间中断会一定程度地影响用户舒适度,只间歇中断,偿价格也最高。Ⅲ类负荷为可转移不可中断负荷,不参与紧急负荷控制。
则负荷中心i切负荷量为:
(1)
式中:PLi,j为负荷中心i的第j类负荷;sch(i,j)为负荷中心i的第j类负荷的控制状态,在负荷中心i参与减负荷控制时,sch(i,1)=1,表示切除Ⅰ类负荷。
1.2 可中断负荷的市场补偿价格模型
依据可中断负荷的市场补偿价格定价机制,单位时间市场价格与负荷水平间呈显著的线性关系,则故障时刻市场价格为ei可表示为:
(2)
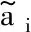
参与减负荷控制时,PLi,0为与PLi无关常量,因此式(2)可转化为:
ei=aiPLi,0+biPLi
(3)
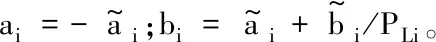
(4)
式中:ei为上述求得的市场补偿价格;PLi为负荷中心i切负荷量。
1.3 紧急减负荷惩罚代价模型
(5)
式中:aci为惩罚系数,一级电网惩罚系数最高,aci,1>aci,2>aci,3,bci,2>bci,3。则事故应缴罚金为:
(6)
式中:PLi为负荷中心i切负荷量;ci为上述所求罚款系数。
1.4 目标函数
当减负荷比例增加时,需支付的可中断负荷补偿价格将减小,而惩罚代价将增大。考虑减负荷的经济性时两目标互相冲突,另外负荷控制应该尽量提高系统静态电压稳定性,为后续直流重启和系统恢复提供有利条件。为此本文在考虑减负荷经济性的同时,将切负荷节点的电压水平也考虑在目标函数内,制定多目标模型。
本文设计的多目标问题可以被描述如下。
minF(x)=[f1(x),f2(x),f3(x)]Tsubject tox∈Ω
(7)
式中:Ω为决策空间,可实现的目标集合;f1(x)为发生故障应缴纳的罚金,f1(x)=Cρ;f2(x)为可中断负荷的补偿金额,f2(x)=CLA;f3(x)为电压薄弱节点集的电压跌落量的平方和。
(8)
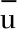
(9)
式中:Zeq,i、ZLi分别为负荷Li对应的等效内阻和等效阻抗。故障发生时系统中δi最大的若干个节点将组成电压薄弱节点集UY。在约束条件中,式(10)为功率平衡约束,式(11)为频率偏差约束。
s.t. PF(PG,PL,fd,U,θ)=0
(10)
|fd|≤ζ
(11)
式中:PG、PL分别为发电机和负荷的有功功率;fd为频率偏差的标幺值;U为节点电压;θ为相位差;fd为频率偏差的标幺值。
2 基于改进NSGA-Ⅱ算法的紧急减负荷控制 优化方法
2.1 基于顺序查找的非支配排序
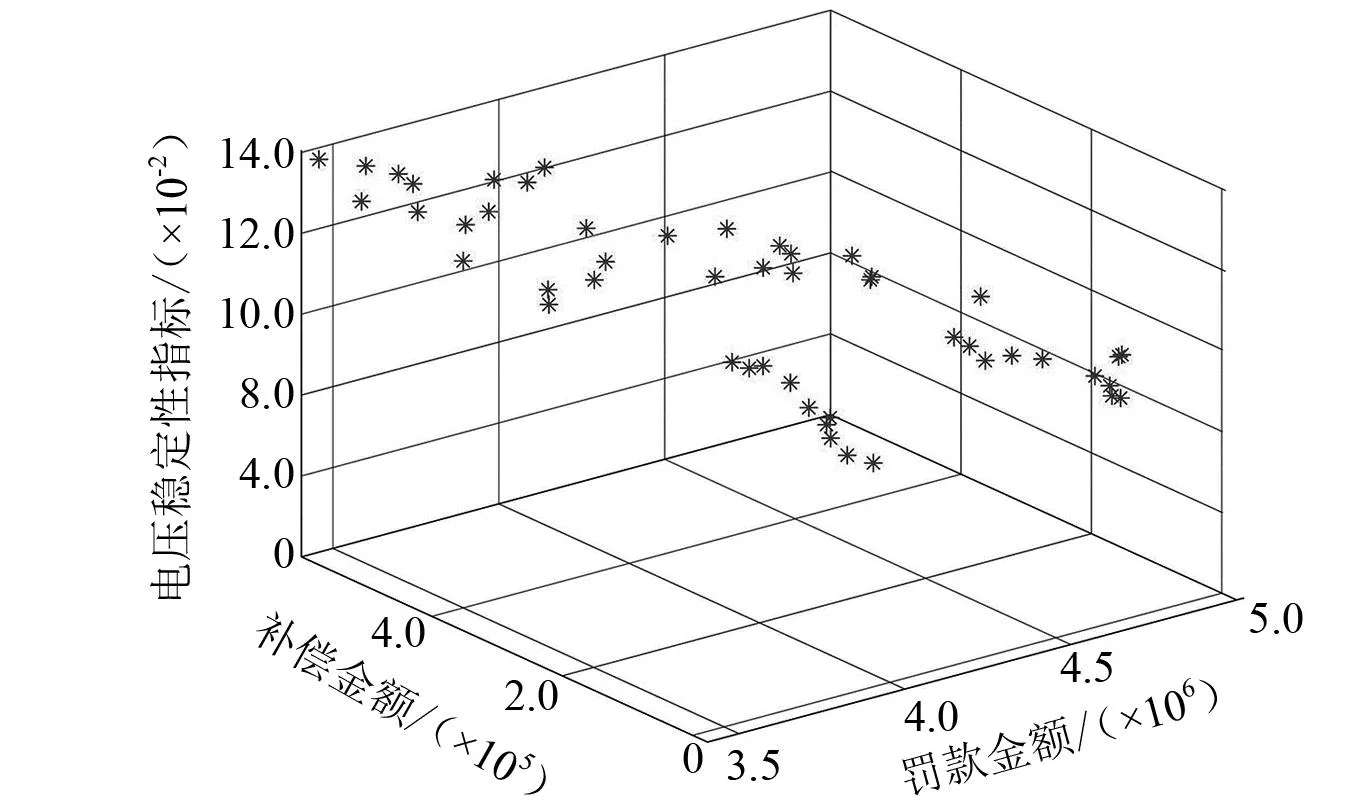
NSGA-Ⅱ算法采用非支配排序,需对两个目标函数分量fi(x)(i=1,2)给定任意两个决策变量集Xa、Xb。对两个目标函数而言,∃i={1,2},fi(Xa)≤fi(Xb)且∀i={1,2},fi(Xa) (12) 式中:q为p的非支配解集的集合;Q为非支配集合所在种群。 在传统NSGA-Ⅱ算法中,采用精英选择策略,而改进后算法采用基于参考点的选取策略,首先通过常规边界交叉法来产生一组均匀的权重向量{ω1...ωi},接着将各维目标值进行自适应归一化。定义种群Rt的理想点为最小值,通过设置一个理想点将目标转化,然后求每个目标函数对应的额外点: (13) Zi,min=s:argmins∈RtASF(s,ω) (14) 式中:Zi,min为第i个目标fi(x)的目标向量;m为维度集合;ωi为权重向量;s为通过参考点选择得到的新解集。将目标i归一化: (15) 式中:ai为目标i的截距,i=1,2,…,m。 如果截距不存在,则设置截距为目标i的最大值。根据参考点得到一组参考线,从中找到离归一化后代的个体最近的参考线,保留对应个体最少的参考点。 改进的NSGA-Ⅱ算法求解流程如图1所示。 图1 改进的NSGA-Ⅱ算法求解流程图 采用改进的NSGA-Ⅱ算法对模型求解,每条染色体代表一种系统事故后切负荷策略,以各机组出力及状态、切负荷量和负荷状态为决策变量,以经济效益和电压稳定性为调度目标,对故障后智能电网切负荷调度策略进行寻优。 将上述方法应用于IEEE 10机39节点系统,设置33-19和35-22为潮流断面,1 s时同时发生短路故障,故障持续时间为1 s。选取母线39为一级电网,1、8、12、21为二级电网,其余均为三级电网,切负荷时以及电网设置惩罚价格最高。 图2为多目标函数的Pareto前沿图,目标函数一为可中断负荷补偿金额,目标函数二为事故缴纳的罚款金额,目标函数三为电压薄弱节点集跌落量。在Pareto前沿中选取三组最优解集,并与改进前算法求解结果对比,A组负荷补偿金额最优,B组事故缴纳罚款最优,C组电压稳定最优。表1为优化效果对比。 表1 优化效果对比 图2 改进后Pareto前沿图 由表1可以看出:采用节点电压稳定性最好的控制方案时,可以使经济效益达到最优,此时控制方案更多地切除了可中断负荷量较大的电压薄弱节点的负荷,在满足经济性的同时,稳定了系统静态电压,为后续系统恢复提供有利条件。且改进后的算法不仅提高了运算效率,还实现了经济最优化。 本文提出了一种协调经济性和系统稳定性的紧急负荷控制多目标优化方法,对传统NSGA-Ⅱ算法进行改进,通过试验结果证明改进后的算法可以有效提高运算速率,且能更好地保证解集均衡分布,有很好的工业应用前景。以IEEE 10机39节点系统为例对算法进行了验证,结果表明算法求得的控制策略可实现协调经济性及电压稳定性的优化控制。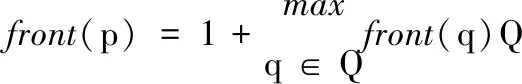
2.2 基于参考点的选择策略

3 算例分析
3.1 模型说明
3.2 仿真分析

4 结束语

