改进灰狼优化最小二乘支持向量机的锂电池剩余寿命预测

郑青根 杨祥国 刘冬 李昕

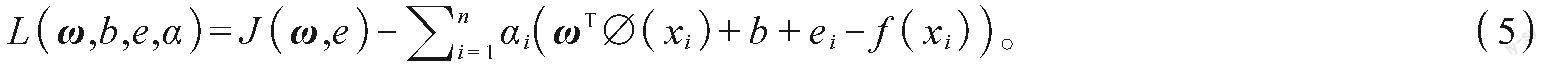
摘要：针对锂电池剩余寿命预测的直接健康因子难以测量以及预测精度不高等问题，提出一种改进灰狼优化最小二乘支持向量机（improved gray wolf optimization least-squares support vector machine， IGWO-LSSVM）的锂电池剩余寿命间接预测方法。该方法从电池放电特性曲线中获取3种表征电池性能退化的间接健康因子，通过引入tent混沌映射、收敛因子非线性递减与莱维飞行策略对灰狼算法加以改进，并结合LS-SVM模型，形成了具有全局优化的改进灰狼优化最小二乘支持向量机的锂电池寿命预测模型。最后利用NASA数据集对文中提出的方法进行了验证，并将实验结果与GWO-LSSVM、PSO-ELM和BP神经网络算法进行了对比分析，试验结果表明文中所提出的改进算法具有更好的预测性能。

关键词：锂电池；剩余寿命；灰狼优化；最小二乘支持向量机；莱维飞行

中图分类号：TM912          文献标志码：A      文章编号：1000-582X（2023）11-078-12

Lithium battery remaining life prediction method based on improved grey wolf optimization least squares support vector machine

ZHENG Qinggen， YANG Xiangguo， LIU Dong， LI Xin

（School of Marine and Energy and Power Engineering， Wuhan University of Technology，

Wuhan 430070， P. R. China）

Abstract： To solve the problem of accurately predicting remaining life of lithium battery， this paper proposes an indirect prediction method based on improved grey wolf optimization least-squares support vector machine （IGWO-LSSVM）. Three indirect health factors characterizing battery performance degradation are derived from discharge characteristic curves. To enhance prediction accuracy， the study incorporates a tent chaotic map， a nonlinear decreasing convergence factor， and a Levi flight strategy into the grey wolf algorithm. Combined with the LSSVM model， the lithium battery life prediction model with global optimization is formed. The proposed method is verified using the NASA data set and compared with GWO-LSSVM， PSO-ELM and BP algorithms. Experimental results show that the improved algorithm proposed in this paper outperforms other methods in terms of prediction accuracy.

Keywords： lithium battery; remaining life; gray wolf optimization; least squares support vector machine; Levy flight

近些年，隨着国家对节能环保理念的推广，电动汽车产业得到了快速的发展，其产量呈现逐年上升趋势[1]，与此同时，作为电动汽车动力源的动力电池也随之得到发展。相较于其他类型的电池，锂离子电池以其优异的储能性能而被选择为电动汽车的动力源[2]。然而，在锂离子电池长期使用的过程中，放电容量会逐渐非线性下降。主要原因包括电极材料腐蚀、电解质变化和分离器老化等，这种非线性容量衰减会导致设备故障甚至造成严重事故。因此，为了减少事故的发生，对电池早期进行准确的剩余寿命预测十分必要。

目前，锂离子电池剩余寿命预测方法可以大致分为2种[3?5]：一是基于模型的方法，通过分析电池物理特性构建电池模型来预测其容量退化趋势，并使用过滤技术来控制参数输出的误差。Thomas等[3]建立了经验模型，通过加速老化实验的数据来预测电池的寿命，描述了循环寿命和不确定性边界。Wang等[4]在建立电池容量状态空间模型的基础上，引入了球形立方粒子滤波器求解，利用状态空间模型外推到指定的故障阈值以确定剩余寿命。然而，这些基于模型的方法虽然具有较高的预测准确性和可信度，但存在参数众多、成本高等问题，而且易受干扰。二是基于数据驱动的方法，该方法不依赖于电池物理模型的精度，它通常从退化数据中提取典型特征建立剩余寿命预测的回归模型[6]。目前，基于数据驱动的方法主要有人工神经网络（artificial neural network，ANN）、支持向量机（support vector machines， SVM）和高斯过程回归（Gaussian process regression，GPR）等方法[7?8]，该类方法主要从数据和经验中学习与改进，而无须构建复杂的电池等效模型，并且电池的特征数据可以实时获得，因此可以用于在线预测电池剩余寿命值。如文献[9?10]都直接利用电池容量作为特征，随后分别采用蚁狮算法与灰狼算法优化支持向量机（support vector machine，SVR）参数，实现对剩余寿命RUL的预测，虽然该类方法能够取得较好的预测效果，但在实际应用中存在电池容量通常难以直接在线获取、基本的智能优化算法存在内部参数容易陷入局部最优以及早熟收敛等问题，并且传统的SVM模型处理大量数据时，求解过程十分复杂，因此该类方法需要进行一定的改进。

针对上述问题，文中提出了一种改进灰狼优化最小二乘支持向量机算法的锂离子电池剩余寿命在线间接预测方法。首先，该方法从锂离子电池放电特性曲线中提取放电温度峰值时间、平均放电电压和等压降时间3种间接健康因子，并与电池容量进行Pearson与Spearman相关性分析；然后，在基本的灰狼优化算法基础上引入tent混沌映射、非线性递减和莱维飞行策略，提出一种基于间接健康因子的IGWO-LSSVM算法，并利用该算法构建出锂离子电池剩余寿命在线预测模型；最后，利用NASA数据集对文中提出的方法进行了验证，并将实验结果与GWO-LSSVM、PSO-ELM、BP神经网络算法进行了对比分析，试验结果表明文中所提出的改进算法具有更好的预测性能。

1 健康因子的选择与相关性分析

1.1 锂离子电池数据集

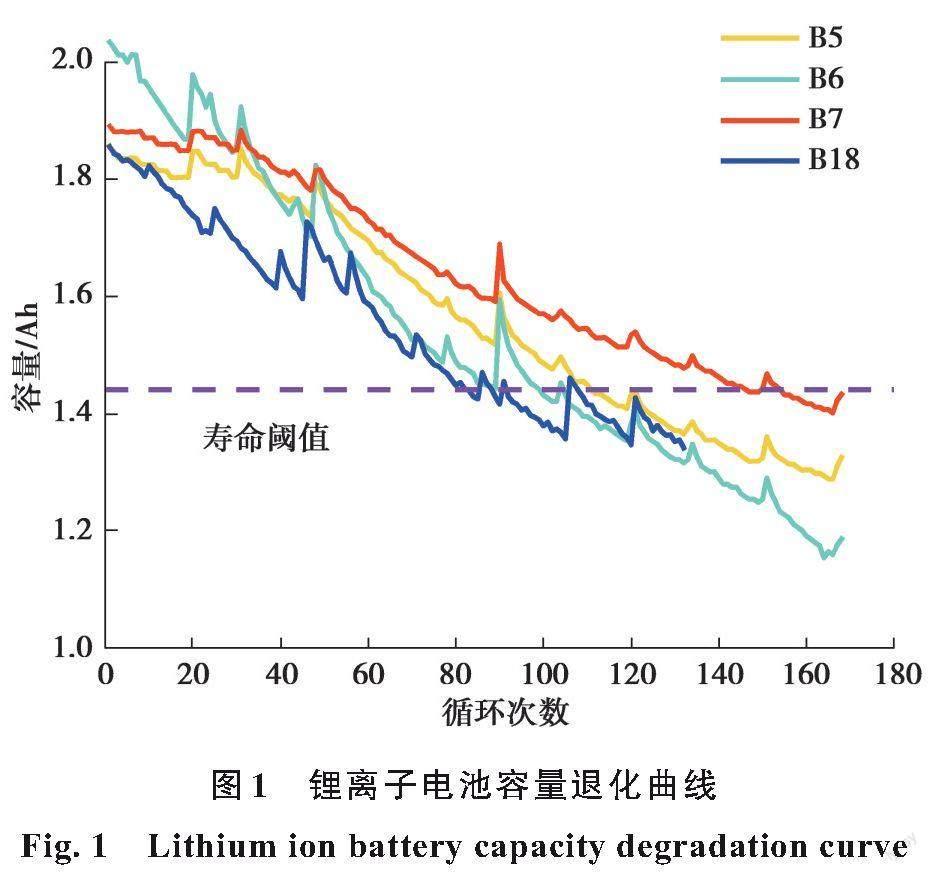
研究选择美国宇航局PCoE 研究中心（National Aeronautics and Space Administration Prognostics Center of Excellence， NASA PCoE）公开的锂离子电池老化试验数据集[10]作为研究对象。该数据由4组额定容量为2 000 mA的18650型号电池（B5、B6、B7、B18）在24 ℃的室温下进行反复充放电实验获得，具体实验过程如下。

充电过程：首先对4组电池以1.5 A恒定电流进行持续性的充电，当4组电池的电压达到4.2 V时，再将电池在4.2 V的恒压模式下进行充电，直至电流逐渐下降到20 mA，则停止充电。

放电过程：将4组电池B5、B6、B7、B18分别在电流强度为2 A的恒流模式下进行放电，直至各自的电压分别降至2.7 V、2.5 V和2.2 V时停止放电。

由于电池容量衰减需要一个长期的反复循环过程，因此将4组电池进行反复地充放电实验，当电池的容量衰减到额定的72%（1.44 Ah）时，认为电池到达失效阈值，则终止实验。电池容量衰减趋势如图1所示。

电池容量与内阻的变化通常作为衡量電池健康状态的直接健康因子，然而这2个参数在实际应用中难以在线实时测量。因此，可以通过对锂离子电池性能衰减过程加以分析，并从中提取间接健康因子。文中分析了锂离子电池放电过程中电池的电压、电流和温度的变化情况，如图2～4所示，选取了放电温度峰值时间、平均放电电压和等压降时间作为3个影响电池性能退化的间接健康因子，分别记为H1、H2与H3。

1.2 Pearson与Spearman相关分析法

为了进一步验证所提的3个间接健康因子与容量之间的相关性，采用Pearson与Spearman相关性分析法作为评价方法。该方法目前已广泛地应用于衡量2个变量之间的线性相关强度[11]，当该系数值为在±0.8～±1之间时，则表示两者之间具有极强的相关性，Pearson的数学原理为

式中：E为期望值；α与β分别为2个长度相同的序列。

Spearman的计算公式为

所提的间接健康因子与容量之间的Pearson与Spearman相关性分析结果见表1所示。

根据表1可知，所提取的放电温度峰值时间H1、平均放电电压H2和等压降时间H3 3个间接健康因子与容量的相关系数均在0.9～1.0之间，因此验证了所提的间接健康因子与容量之间存在较高的相关性，可以用来预测锂离子电池的剩余寿命值。

2 IGWO-LSSVM预测模型的建立

2.1 最小二乘支持向量机

LS-SVM是Suykens和Vandewalle在传统的SVM模型的基础上提出的一种新型支持向量机算法[12?16]。LS-SVM主要原理是将SVM模型中的不等式约束改为等式约束，将误差平方和损失函数作为训练集的经验损失，在保证计算精度的前提下，将解二次寻优问题转化为求解线性方程组问题。假设在特征空间中，给定一个数据样本为D={x_i，f（x_i）}，x_i是第i样本的输入量，f（x_i）是x_i对应的输出，则LSSVM模型的回归表达式为

式中：ω为权值向量；b为偏差值；?（x_i）为映射函数。基于结构风险最小化原则，确定了模型参数ω、b，并选取误差e_i的二次函数作为损失函数，将LSSVM回归问题转化为式（4）的约束优化问题。

式中：e_i为模型的训练误差；C为正则化参数。引入拉格朗日方程将式（4）转化为二次规划问题

式中：α为拉格朗日乘子，通过库恩-塔克条件（KKT），对式（5）进行求导，可得

将式（6）进行线性方程组求解，可得：

式中，K为核函数矩阵。通过实验对比不同类型的核函数，选择具有抗干扰能力强以及参数设置少等优点的径向基RBF作为模型核函数，即：

结合Mercer条件，得到该LSSVM的模型为：

经过以上的推导，将LSSVM回归模型由式（3）转化成式（9），考虑到该模型的参数选择对预测精度至关重要，采用灰狼优化算法对LSSVM中的正则化因子C和核参数σ进行优化，并且选择输出值与实际值的均方根误差作为模型的自适应函数值。

2.2 灰狼优化算法

灰狼优化算法属于一种元启发式算法，其灵感源于灰狼的等级结构和社会狩猎行为，因其具有全局优化、易于编程、需要调整的参数少等优点而被广泛应用[17?18]。其原理可简述为：在一个待求解的D维问题上，狼群通过计算在不同位置的自适应值大小将狼群依次划分为α狼、β狼、δ狼和ω狼，整个狼群的捕食决策由前三者做决定，其余狼群负责对猎物进行围攻。捕食过程可以分为以下3个阶段。

1）对猎物进行围攻。

D（t）=|CX_p （t）-X（t）|， （10）

X（t+1）=X_p （t）-AD（t）， （11）

式中：t为当前迭代次数；D表示狼群与猎物间的距离；X_p为猎物的位置向量；X为灰狼的位置向量；A与C是系数向量，定义为

A=2ar_1-a， （12）

C=2r_2。 （13）

式中：a=a_0 （1-t/T_max），随着迭代次数的增加，a从2减少到0；r_1和r_2的取值范围为0～1；T_max为总迭代次数。

2）捕猎过程。

前3个等级的狼群寻找方向朝猎物逐渐靠近，该过程的数学表达式为

式中：X_a、X_β和X_δ分别为α、β和δ狼的最优位置；D_α、D_β和D_δ为前3只最优狼与种群的距离。然后，在α、β和δ狼的领导下，更新灰狼种群的位置

式中：A1、A2、A3为由式（12）计算得到的不同系数；X1、X2、X3分别为α、β、δ领导下的更新位置。

3）对猎物发起攻击。

随着对猎物的逼近α的值线性减小，对应的|L|也在[-α， α]内变化。当|L|<1时，算法收敛，获得猎物位置。

2.3 灰狼优化算法的改进

采用基本的狼群优化算法对LS-SVM模型进行寻优的过程中存在目标值易陷入局部最优解和收敛速度慢等问题，为解决该问题，笔者在基本的狼群优化算法基础上引入tent混沌映射、收敛因子非线性调整机制和莱维飞行等方法来构建新的灰狼优化算法，新构建的算法具有较快的收敛速度和良好的全局寻优能力。

2.3.1 Tent混沌映射

为了改善基本的灰狼优化算法在初始化狼群时物种总体的多样性与适用性，并提供具有均匀分布的初始总体，以及避免困在局部最优值中，提高算法的求解效率，结合探索过程中的混沌随机性和遍历性特点，将tent混沌映射方法[19]融入到灰狼优化算法中，其数学表达式为

2.3.2 收敛因子非线性调整策略

收敛因子的大小对于算法的优化至关重要。当a>1时，可以使得算法保持较高的全局优化与搜索能力；当a≤1时，算法局部优化与搜索能力加强，收敛速度增加。然而，传统的灰狼优化算法线性收敛因子随着迭代次数的增长而线性减少，不能完全反映真實的优化过程，而且还存在收敛速度慢、不稳定和容易落入局部最优等问题。为了解决这些问题，并在全局和局部勘探能力之间做出适当的权衡，引进收敛因子非线性调整策略，其公式为

式中：a_ini与a_final分别为非线性因子初值与终值；u与λ为调节参数；T_max为最大迭代次数。

该非线性递减策略通过结合正弦函数可以使得收敛因子在起始阶段递减较慢从而保持全局搜索与优化的能力（a>1），而在后期递减较快，可以提高算法的收敛速度（a≤1）。

2.3.3 莱维飞行策略

为了提高灰狼优化算法寻优过程中整体的寻优能力，避免狼群陷入局部最优解，在灰狼算法的基础上引入莱维飞行算法[20]。该算法具有小步长时间随机行走搜索和大步长时间突然方向跳跃的特点。莱维飞行策略的具体表达式为：

式中：x_i^' （t+1）表示经过莱维飞行算法更新之后的位置；α为步长控制因子；λ为步长；⊕表示点积运算；L（λ）表示莱维分布的路径，且满足以下条件

L（λ）～u=t^（-λ），       1≤λ≤3。 （20）

考虑到莱维飞行分布复杂性的特点，现如今主要通过采用Mantegna算法对其进行模拟，具体表达形式为

式中，μ与v为正态分布，μ～N（0，σ_μ^2），v～N（0，σ_v^2），其中

其中，β为[0，2]的随机数。

2.4 IGWO-LSSVM算法

通过引入tent混沌映射、收敛因子非线性调整机制和莱维飞行方法对基本的灰狼算法进行改进，使得LS-SVM模型参数能够获得更好的参数，具体流程如图5所示。

主要步骤如下：

1）数据预处理。对原始数据进行预处理，按照不同的比例分为训练集与测试集。

2）设置灰狼优化算法的基本参数。最大迭代次数M=50，狼群数量N=20，维度D=2，上界U=100，下界L=0.001。

3）设置自适应度函数。选择锂离子电池实际容量值与模型预测容量值之间的均方误差作为本算法中的自适应度函数，表达式为

式中：y ?_i表示预测值；y_i表示实际值。

4）改进灰狼优化算法优化LS-SVM模型参数。利用tent混沌映射对种群进行初始化，根据自适应值的大小设置狼群等级，引入莱维飞行对种群位置进行更新，在反复的迭代过程中找到最优参数。

5）锂电池剩余寿命预测。在Matlab平台上使用测试集数据对IGWO-LSSVM模型进行验证，完成锂电池剩余寿命预测。

3 算法有效性与准确性验证

为了验证所提算法的有效性与准确性，笔者从NASA PCoE研究中心公开的锂离子电池老化试验数据集中提取4组电池的放电温度峰值时间H1、平均放电电压H2和等压降时间H3作为模型的输入，并以容量作为输出，建立了基于IGWO-LSSVM锂电池寿命预测模型。在本次实验中，选择B5、B6、B7的3组电池前85个循环以及B18电池前67个循环数据作为模型的训练样本，4组电池的其余样本均作为测试样本。在预测过程中，规定锂离子电池容量衰减到额定容量的72%（1.44 Ah）时，则认为锂离子电池达到寿命阈值。为了验证文中所提算法的有效性，将该方法分别与GWO-LSSVM、PSO-ELM算法、BP神经网络进行对比分析，不同方法的预测结果如图6～9所示。

根据图6～9可知，当选择锂离子电池的前85个（B5、B6、B7），67个（B18）周期作为训练样本时，相较于GWO-LSSVM、PSO-ELM算法和BPBP神经网络算法，文中提出基于IGWO-LSSVM算法的预测效果更佳。为了更好地分析4种不同算法的预测效果，对4种算法的预测结果进行了数据分析，具体结果如表2所示（—表示无法预测）。其中锂电池剩余寿命RRUL为预测起点到达寿命阈值所对应的循环周期，其表达式为

式中：PRUL為预测剩余寿命；RRUL为实际剩余寿命；Er为绝对误差；Per为相对误差。

根据表2的预测结果分析可知，在4组电池的预测结果中，文中所提的IGWO-LSSVM的整体预测性能相对最佳。以B5号电池为例，当以第86个循环周期为预测起点时，电池实际的RRUL值为25，GWO-LSSVM、PSO-ELM、BP神经网络 3种算法的RRUL值分别为28、21、21，其Er值和Per值分别为3和12%、4和16%、4和16%，而IGWO-LSSVM算法所预测的RRUL值为27，Er值和Per值分别为2和8%，相对于其他3种算法，IGWO-LSSVM的Er值和Per值的相对误差分别减小了33.3%和50%。然而，如果单独从RRUL的预测精度来评估4种算法的预测精度，则由B6号电池的预测结果可以发现，虽然BP算法与IGWO-LSSVM算法的Er值和Per值相同，但是结合图8实际的预测结果可知，IGWO-LSSVM算法所预测的容量值与真实值更为接近。因此，为了全方位对文中所提的方法进行有效验证，本研究引入均方根误差R_MSE与平均绝对误差M_AE作为算法整体预测性能的评估标准，其数学式表达式为

由表3分析可知，在4种算法预测锂离子电池寿命中，GWO-LSSVM、PSO-ELM、BP神经网络 3种算法的MAE与RMSE值均比IGWO-LSSVM算法大。以RRUL值最小的B6为例，BP与PSO-ELM算法的MAE与RMSE值分别为0.047 3和0.073 0、0.026 9和0.034 4，均比IGWO-LSSVM的MAE值与RMSE值大；GWO-LSSVM算法的MAE值为0.022 4，而IGWO-LSSVM的MAE值为0.014 3，仅为GWO-LSSVM的2/3，与GWO-LSSVM算法相比，IGWO-LSSVM的RMSE值减少约30%。通过以上分析可知，文中所提的IGWO-LSSVM算法均比GWO-LSSVM、PSO-ELM、BP神经网络算法具有更高的预估精度。为了进一步验证IGWO-LSSVM算法的预测性能，则缩减4组电池的训练样本，从85（B5、B6、B7）与66（B18）个循环周期分别减少至66（B5、B6、B7）与53（B18）个周期，预测结果如图10～13所示。由图可知，当减少模型的训练样本之后，该模型仍具较好的预测性能，其详细的性能指标见表4所示。

通过分析表4可知，当减少4组锂离子电池的训练样本后，IGWO-LSSVM算法仍获得较好的剩余寿命预测结果。最大的绝对误差Er不超过3，最大相对误差不超过10%，而GWO-LSSVM、PSO-ELM和BP神经网络算法的总体预测精度出现较大的降低。以B7号电池为例，选取前67个循环周期为训练样本时，PSO-ELM与BP算法出现无法预测的情况，GWO-LSSVM算法的Er值和Per值高达14和17.70%；而所改进的GWO-LSSVM算法的Er值和Per值分别为3和3.79%。可见，IGWO-LSSVM算法的预测误差明显低于GWO- LSSVM、BP和PSO-ELM算法；再以B6号电池为例，结合表4可知，BP算法的Per值最小。但结合图11容量整体的预测结果发现，BP算法在预测后期出现误差剧增，而IGWO-LSSVM算法仍保持较好的剩余寿命预测性能，并且在预测后期始终可以精准地预估电池容量衰减情况。

因此，为了进一步论证缩减训练样本之后，文中所提算法仍具有较好的预测性能，则分别对4种不同算法的MAE与RMSE值进行分析，其具体分析结果见表5所示。

由表5可以发现，当选择前66个循环周期数据作为训练样本时，文中所提出的IGWO-LSSVM算法的平均误差MAE值与均方根误差RMSE值最小。以B6号电池为例，GWO-LSSVM算法的MAE值和RMSE值分别为0.028 5和0.034 4，而IGWO-LSSVM算法的MAE值和RMSE值分别为0.016 2和0.022 9，相对百分比分别下降了43.2%和33.4%，比PSO-ELM算法分别下降了43.5%和34%。与BP算法比较，结合表4可知，虽然BP算法的预测Per值最小，但其MAE和RMSE值分别高达0.083 0和0.117 8，而IGWO-LSSVM算法的MAE值与RMSE值仅为其1/5。因此，单从Er值和Per值不能全方位对不同算法的预测精度进行有效评估，还需从平均误差与均方根误差进行整体评估。通过以上一系列的实验结果分析可知，相比于GWO-LSSVM、PSO-ELM和BP神经网络算法，文中所提的IGWO-LSSVM算法对于锂离子电池剩余寿命预测具有更高的预测精度。

4 结 论

为了提高锂离子电池剩余寿命的预测精度，降低意外事故发生的概率，在GWO-LSSVM算法的基础上，提出了一种改进灰狼优化最小二乘支持向量机算法的锂离子电池剩余寿命在线间接预测方法IGWO-LSSVM。IGWO-LSSVM方法通过提取放电平均电压、放电温度峰值时间和等压降所需时间作为3个间接的健康因子，并采用Pearson与Spearman相关系数法对健康因子与容量之间的关系进行相关性分析，将间接健康因子作为输入，容量作为输出，对锂离子电池剩余寿命进行预测。文中方法在基本的GWO基础上引入tent混沌映射、非线性递减和莱维飞行策略，解决了传统的GWO算法存在初始化种群比较单一以及迭代后期容易陷入局部最优解问题，建立了IGWO-LSSVM算法模型。利用NASA提供的数据集对文中所提的方法进行了验证性实验，并将实验结果与GWO-LSSVM、PSO-ELM和BP神经网络算法进行了比较分析，验证了文中所提IGWO-LSSVM算法预测精度更高。得出如下结论：

1）通过Pearson与Spearman相关系数分析法验证了平均放电电压、放电温度峰值时间和等压降时间3个间接健康因子与容量具有较强的相关性，可作为锂离子电池剩余寿命在线预测的间接健康因子。

2）在GWO算法的基础上引入tent混沌射、非线性递减和莱维飞行策略，可以有效的解决GWO寻优过程容易陷入局部最优解问题，从而增强了算法全局搜索的能力。

3）基于IGWO-LSSVM算法的锂离子电池剩余寿命在线间接预测方法，与其他算法相比，具有更高的预测精度。

参考文献

［1］  马建， 刘晓东， 陈轶嵩， 等.中国新能源汽车产业与技术发展现状及对策[J].中国公路学报， 2018， 31（8）： 1-19.

Ma J， Liu X D， Chen Y S， et al. Current status and countermeasures for Chinas new energy automobile industry and technology development[J].China Journal of Highway and Transport，2018，31（8）：1-19. （in Chinese）

［2］  庞辉， 郭龙， 武龙星， 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报， 2021， 36（10）： 2178-2189.

Pang H， Guo L， Wu L X， et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society， 2021， 36（10）： 2178-2189.（in Chinese）

［3］  Thomas E V， Bloom I， Christophersen J P，et al.Statistical methodology for predicting the life of lithium-ion cells via accelerated degradation testing[J].Journal of Power Sources， 2008，184（1）：312-317.

［4］  Wang D， Yang F F， Tsui K L， et al. Remaining useful life prediction of lithium-ion batteries based on spherical cubature particle filter[J]. IEEE Transactions on Instrumentation and Measurement， 2016， 65（6）： 1282-1291.

［5］  Guha A， Patra A.Online estimation of the electrochemical impedance spectrum and remaining useful life of lithium-ion batteries[J].IEEE Transactions on Instrumentation and Measurement，2018，67（8）：1836-1849.

［6］  Li X， Ma Y，Zhu J J.An online dual filters RUL prediction method of lithium-ion battery based on unscented particle filter and least squares support vector machine[J].Measurement， 2021，184：109935.

［7］  徐佳寧， 倪裕隆， 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J].电工技术学报， 2021， 36（17）： 3693-3704.

Xu J N， Ni Y L， Zhu C B. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transactions of China Electrotechnical Society， 2021， 36（17）： 3693-3704. （in Chinese）

［8］  Patil M A， Tagade P， Hariharan K S， et al.A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation[J].Applied Energy，2015， 159：285-297.

［9］  王瀛洲， 倪裕隆， 郑宇清， 等. 基于ALO-SVR的锂离子电池剩余使用寿命预测[J].中国电机工程学报，2021，41（4）：1445-1457，1550.

Wang Y Z， Ni Y L， Zheng Y Q， et al. Remaining useful life prediction of lithium-ion batteries based on support vector regression optimized and ant lion optimizations[J]. Proceedings of the CSEE， 2021， 41（4）： 1445-1457， 1550. （in Chinese）

［10］  杨战社， 王云浩， 孔晨再. 基于GWO-SVR的锂电池剩余使用寿命预测[J].电源学报， 2023， 21（2）：154-162.

Yang Z S， Wang Y H， Kong C Z. Prediction of remaining useful life of lithium-ion batteries based on GWO-SVR method[J]. Journal of Power Supply， 2023， 21（2）：154-162. （in Chinese）

［11］  宁青菊， 施梦琢， 史永胜， 等. 基于最优充放电曲线的锂离子电池寿命预测方法[J].陕西科技大学学报，2021，39（2）： 153-160.

Ning Q J， Shi M Z， Shi Y S， et al. Lithium-ion battery life prediction method based on optimal charge and discharge curve[J]. Journal of Shaanxi University of Science & Technology， 2021， 39（2）： 153-160. （in Chinese）

［12］  Wang Q， Ye M， Wei M， et al.Co-estimation of state of charge and capacity for lithium-ion battery based on recurrent neural network and support vector machine[J].Energy Reports，2021，7：7323-7332.

［13］  王萍， 张吉昂， 程泽. 基于最小二乘支持向量机误差补偿模型的锂离子电池健康状态估计方法[J]. 电网技术， 2022， 46（2）： 613-623.

Wang P， Zhang J， Cheng Z. State of health estimation of Li-ion battery based on least squares support vector machine error compensation model[J]. Power System Technology， 2022， 46（2）： 613-623.（in Chinese）

［14］  姜滨， 孙丽萍， 曹军， 等. 基于PSO优化LS-SVM的木材含水率软测量建模[J]. 重庆大学学报， 2016， 39（1）： 48-54.

Jiang B， Sun L P， Cao J， et al. Soft sensor model for wood moisture content based on LS-SVM optimized by PSO[J]. Journal of Chongqing University， 2016， 39（1）： 48-54.（in Chinese）

［15］  杨晓敏. 改进灰狼算法优化支持向量机的网络流量预测[J].电子测量与仪器学报， 2021， 35（3）： 211-217.

Yang X M. Improved gray wolf algorithm to optimize support vector machine for network traffic prediction[J].Journal of Electronic Measurement and Instrumentation， 2021， 35（3）： 211-217. （in Chinese）

［16］  赵超， 戴坤成. 自适应加权最小二乘支持向量机的空调负荷预测[J]. 重庆大学学报， 2016， 39（1）： 55-64.

Zhao C， Dai K C. Modeling air-conditioning load forecasting based on adaptive weighted least squares support vector machine[J]. Journal of Chongqing University， 2016， 39（1）： 55-64. （in Chinese）

［17］  Chen G J， Liu Y H， Wang S C， et al. Searching for the optimal current pattern based on grey wolf optimizer and equivalent circuit model of Li-ion batteries[J]. Journal of Energy Storage， 2021， 33：101933.

［18］  Miao D， Hossain S. Improved gray wolf optimization algorithm for solving placement and sizing of electrical energy storage system in micro-grids[J]. ISA Transactions， 2020， 102： 376-387.

［19］  滕志軍， 吕金玲， 郭力文， 等.一种基于Tent映射的混合灰狼优化的改进算法[J].哈尔滨工业大学学报， 2018， 50（11）： 40-49.

Teng Z J， Lü J J， Guo L W， et al. An improved hybrid grey wolf optimization algorithm based on Tent mapping[J]. Journal of Harbin Institute of Technology， 2018， 50（11）： 40-49. （in Chinese）

［20］  李彦苍，徐培东.基于自适应步长和莱维飞行策略的改进狼群算法[J/OL].重庆大学学报：1-18[2022-06-22]. http：//kns.cnki.net/kcms/detail/50.1044.N.20210608.0958.002.html.

Li Y C， Xu P D. Improved wolf pack algorithm based on adaptive step size and levy flight strategy[J]. Journal of Chongqing University：1-18[2022-06-22]. http：//kns.cnki.net/kcms/detail/50.1044.N.20210608.0958.002.html.（in Chinese）