采用基本环境参数的导线覆冰预测方法

韩兴波 陈孜铭 邢镔 蒋兴良

摘要：风速、温度、空气中液态水含量和水滴中值体积直径等4项参数是影响导线覆冰的主要环境参数。根据空气中水滴运动、碰撞和冻结进而形成导线覆冰的过程，基于流体力学和热平衡建立了“四参数”导线覆冰模型，通过数值计算详细分析了各个环境参数对导线覆冰增长速率的影响特性，并结合线路实际监测数据分析并拟合了液态水含量和水滴中值体积直径的经验公式，进而建立基于基本环境参数（一般传感器可获得的环境参数）的导线覆冰预测模型。研究结果表明：水滴中值体积直径对导线覆冰速率的影响具有饱和特性，空气中液态水含量的变化和风速、温度和湿度具有一定相关性。研究结论为输电线路覆冰预测、预警工作提供了理论参考。

关键词：输电线路；覆冰预测；环境参数；模型

中图分类号：TM85          文献标志码：A      文章编号：1000-582X（2023）11-069-09

Prediction model of conductor icing based on basic environmental parameters

HAN Xingbo1，2， CHEN Ziming2， XING Bin1， JIANG Xingliang3

（1. Chongqing Innovation Center of Industrial Big-Data Co.， Ltd.， National Engineering Laboratory for Industrial Big-data Application Technology， Chongqing 400707， P. R. China; 2. School of Mechatronics and Vehicle Engineering， Chongqing Jiaotong University， Chongqing 400074， P. R. China; 3. Xuefeng Mountain Energy Equipment Safety National Observation and Research Station， Chongqing 400044，P. R. China）

Abstract： Wind speed， temperature， air liquid water content， and median volume diameter of water droplets are the main environmental parameters influencing conductor icing. This paper establishes a “four-parameter” model for wire icing using principles from fluid mechanics and thermal equilibrium considering the motion， collision， and freezing processes of water droplets. Through numerical computations， the study analyzes the unique impacts of each environmental parameter on the growth rate of conductor icing. Additionally， empirical formulas for liquid water content and median volume diameter of water droplets are developed based on practical line monitoring data. Subsequently， a predictive model for conductor icing is devised， relying on readily obtainable sensor data. Research findings reveal that the influence of the median volume diameter of water droplets on the rate of conductor icing exhibits a saturation characteristic， while variations in air liquid water content correlate with wind speed， temperature， and humidity. These conclusions provide a theoretical foundation for predicting and early warning systems for icing on transmission lines.

Keywords： transmission line; icing prediction; environmental parameters; model

中國南方地区输电线路冬季结冰现象十分常见，在“新基建”背景下，中国输电线路建设规模和覆盖范围不断扩大，而局部区域快速增长的覆冰可在短时间内导致金具损坏、导线断裂、杆塔倒塌，严重威胁下输电线路的安全稳定运行[1]。随着全球气候变化和“小冰期”的到来，电网冬季覆冰成为新常态并逐步由南向北发展[2]，例如，2020年11月吉林遭受强冰冻天气侵袭，覆冰造成325条次线路跳闸，30万用户断电，人民生产、生活受到严重影响。

电网覆冰问题由来已久，在国内外均有大量的研究基础和防治方案，但均没有实现线路覆冰问题的完全解决。准确、及时和高效的输电线线路覆冰预测是电网冰害预警的重要基础，也是防、除冰措施合理应用和布置的重要依据。早期的线路覆冰预测主要以经验公式为主，例如Langmuir-Blodgeet公式[3]、Cansdale等[4]和Jones[5]公式等，预测精度不一，适用范围也十分有限。Makkonen[6]认为，线路覆冰发展在微观上取决于空气中过冷却水滴的运动和碰撞，并试验研究了粗糙度对圆柱体覆冰的影响、冰凌的生长规律以及结冰热传导[7]等基础问题。在此基础上，基于流体力学和热力学，从水滴碰撞、捕获和冻结角度出发，Finstad等[3]和Makkonen[8]建立了较为准确的输电线路覆冰计算模型，较好地反映了导线表面覆冰产生的物理过程。此外，导线覆冰的形态和速率还受到导线本身运行工况的影响，何高辉等[9]通过试验研究发现，电晕在一定程度上会抑制导线覆冰的增长速率。毕聪来等[1]通过试验和数值模拟，研究了导线直径对其覆冰速率的影响规律，并提出了利用扩径导线进行防冰的方法。金海云等[10]反向利用了超疏水铝表面的水滴滑落现象，研究了利用超疏水铝进行导线防冰的可行性。

为进一步优化Makkonen导线覆冰模型，使之更适用于工程实践，国内许多学者做了大量研究。郭昊等[11]对导线雾凇覆冰时的水滴碰撞系数进行了拟合。刘春城等[12]假设水滴冻结系数为1，建立了非均匀椭球形雨凇覆冰的计算模型。蒋兴良等[13]探讨了时间步长对导线覆冰预测的影响，通过平衡和时间成本和计算精度获得了最优的仿真时间步长。Zhang等[14]通过建立导线二维湍流场仿真计算模型，模拟了水滴碰撞导线的过程，分析并获得了不同铝绞线匝数下导线水滴碰撞系数的变化规律。为提高水滴冻结系数的计算准确度，何青等[15]通过考虑水滴碰撞系数、环境参数、电流焦耳热等因素的影响，获得了水滴冻结系数随导线直径的变化规律。此外，He等[16]以分裂导线雾凇覆冰为对象，仿真研究了不同分裂间距子导线表面局部碰撞系数的分布特征，为提高导线覆冰预测的精度奠定了基础。

为了实时、动态地模拟导线覆冰过程，梁曦东等[17]、王强等[18]和蒋兴良等[13]均建立了基于空气中液態水含量w（g/m3）、环境温度T（℃）、风速U（m/s）和水滴中值体积直径dMVD（median volume diameter， MVD）4项环境参数的覆冰数值计算模型，导线覆冰形态、重量等仿真结果和试验结果吻合度较好。但实际上，在4项环境参数中w和dMVD的获得是比较困难的，一般的气象传感器在覆冰条件下只能获得U、T和环境湿度等参数。韩兴波等[19]通过旋转多导体装置监测覆冰质量，从而反算得到了4项环境参数，但装置的监测实时性和精度仍有待提高。

为将当前输电线路导线覆冰预测模型更好地和工程运用相结合，考虑覆冰条件下部分环境参数难以获得的实际情况，笔者基于“四参数”导线覆冰模型，通过数值计算详细分析了各个环境参数对导线覆冰增长过程的影响程度，在此基础上建立基于基本环境参数（一般传感器可获得的环境参数）的导线覆冰预测模型，并通过线路实际监测覆冰数据进行验证，从而提高当前导线覆冰模型的工程实用性，为输电线路覆冰预测、预警工作提供理论参考。

1 基于4项环境参数的导线覆冰模拟

1.1 基于4项环境参数的导线覆冰模型

空气中随气流运动的过冷却水滴在导线表面的绕流、碰撞、捕获和冻结过程决定了覆冰增长的形态和速率。为获得水滴的碰撞系数α1，需求解导线外部的气流-水滴二相流场，当前主要利用CFD （computational fluid dynamics）软件求解Navier-Stokes方程，利用欧拉法或拉格朗日法求解水滴和气流的耦合关系[20]为

式中：vw和v分别是水滴和气流速率，m/s；ρw和ρa分别是水滴和气流的密度，kg/m3；f（v-vw）为气流对单位质量水滴的拽力，N/kg；F为非稳态阻力项，N/kg。根据该过程可知，碰撞系数α受到风速、dMVD和导线直径的影响。在α1已知后，需根据热平衡方程[15]求解水滴的冻结系数α3（不考虑导线表面的粗糙度及有无水膜，捕获系数α2≈1），因此，α3主要受到环境温度影响。根据式（2）确定导线覆冰增长速率，覆冰密度可根据π理论[19]获得。

上述过程具体步骤如图1所示。可以看到，即使可以准确地获得4项环境参数，基于4项环境参数的导线覆冰模拟需要包括流场计算和热平衡计算，且在覆冰形态改变后，需重新计算流场及相关水滴碰、冻系数，过程较为复杂繁琐。

1.2 4项环境参数对导线覆冰的影响

为明确4项环境参数（特别是不易获得的dMVD和w）对导线覆冰增长过程的影响，以20 mm直径导线为例，按照图1所示过程进行计算，得到结果如图2和图3所示。

如图2所示，在导线严重覆冰最易发生的温度范围（0 ℃以下且接近0 ℃）内，dMVD对导线覆冰速率dM/dt的影响存在饱和特性，在dMVD≤10 μm时，覆冰速率dM/dt较小，在10 μmDx后，dM/dt保持不变。临界值Dx受到风速和温度的影响，风速越大、温度越高，Dx越小，dM/dt快速增长区间也越小。同样，当改变w时（如图3），dM/dt快速增长区间受风速和温度影响，风速越大、温度越高，则dM/dt快速增长区间越狭窄，即dM/dt受到w变化的影响越小。

因此，根据上述仿真结果可以推测，dMVD和w可影响导线覆冰速率，但其影响程度受到风速和温度控制，在风速较大、温度接近0 ℃时（严重覆冰发生的条件），dMVD和w对覆冰速率的影响程度是较小的。

2 基于基本环境参数的导线覆冰预测

2.1 导线覆冰预测模型

根据上述结果过程可知，导线覆冰数值模拟过程较为复杂、计算量大，不利于线路覆冰的实时预测，因此，考虑运用基于粒子群算法的BP神经网络建立导线覆冰预测模型。但是，当前输电线路导线覆冰实测数据均较为分散，难以用于建立神经网络模型。因此，笔者选择从数值模拟角度出发，按图1所示流程，通过改变4项环境参数和导线直径，仿真获得大量导线覆冰数据；采用基于粒子群算法的BP神经网络[21]建立4项环境参数和导线覆冰速率的映射关系。

如图4所示，设置导线直径的变化范围为5～120 mm，风速为2～30 m/s，温度为-15～-1 ℃，dMVD为5～60 μm，w为0.1～6 g/m3。利用图1所示模型进行计算，获得34 560组数据，随机抽取其中20 000组数据进行模型训练，得到4项环境参数和导线覆冰覆冰速率的映射关系NET；另外14 560组用于验证。由图5可知，在不同环境条件下模型预测的准确度不同，在dMVD>10 μm或w<2.5 g/m3条件下，预测精度较高，而在dMVD≤10 μm或w≥2.5 g/m3条件下，预测精度有所降低。但总体精度较高，数值仿真所得dM/dt和本预测模型所得结果的绝对误差Error最大值为0.48 g/min，最小值为2.68×10-7 g/min，平均误差为0.39 g/min。

在4项环境参数已知条件下，利用基于粒子群算法的BP神经网络预测模型（NET-1）替代繁杂的数值模拟过程，实现对导线覆冰速率的快速预测。但通常较易获得的环境参数只有风速、温度和空气相对湿度等，若仍要利用该模型，则需进一步建立一般环境参数（U、T和相对湿度H）和4项基本环境参数（U、w、dMVD和T）的映射关系NET-2，具体如图6所示。

根据图2和图3计算结果，dMVD和w对导线覆冰速率的影响并非独立于风速和温度，且从实际情况看，当风速较小时，气流携带过冷却水的能力有限，随气流运动至碰撞到导线的水滴数量少，对应的气流的液态水含量w也较小。当风速较大时，气流携带的水滴数量增大，而水滴中值体积dMVD减小，气流中总的液态水含量w增大。

根据文献[22]试验研究结论，形成覆冰的过冷却水滴中值体积直径范围为dMVD=5～50 μm，且dMVD的分布范圍和风速密切相关，两者关系为

dMVD = 39 - 1.4U + 0.04U 2 ， 0 m/s ≤ U ≤ 20 m/s。（3）

不同于dMVD，除去风速的作用，气流中的液态水含量w还受环境温度T和相对湿度H的影响。在空气相对湿度较高时，气流中的w随着风速的增大而增大，而当空气相对湿度较低时，w维持在较小值，导线不易形成覆冰。根据韩兴波等[19]长期在雪峰山的观测结果（部分数据如图7所示），文中拟合了空气中液态水含量w的表达式：

根据式（3）～（4）建立起一般容易获得的环境参数（U、T和相对湿度H）与覆冰基本环境参数（U、w、dMVD和T）的映射关系NET-2。

2.2 预测模型的验证

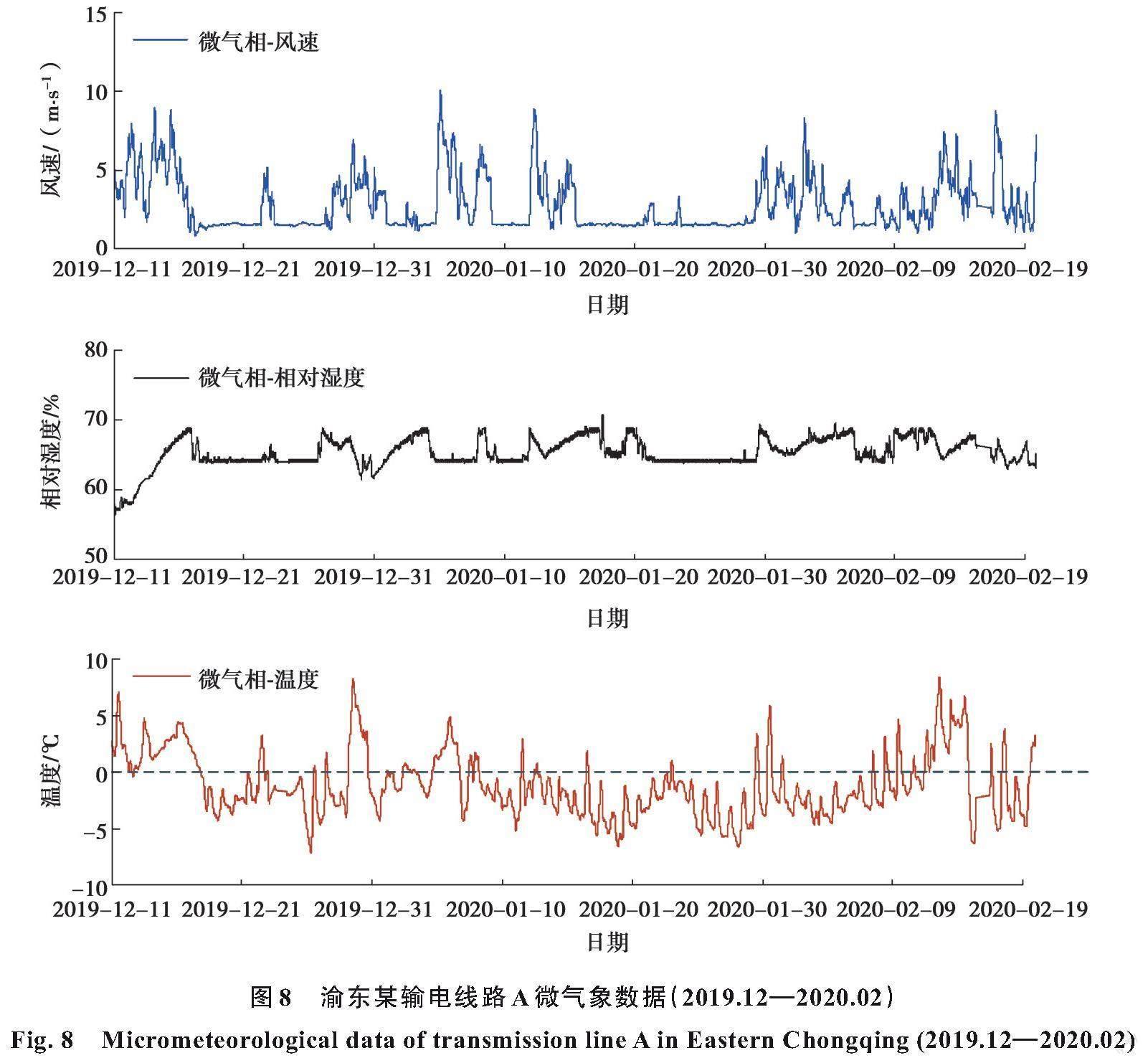
文中利用中国渝东地区某条输电线路（记作A）覆冰监测数据作为样本，配合该地区基本环境参数的监测结果，对上述导线覆冰预测模型进行验证。如图8所示，将渝东某线路A在2019年底—2020年初的微气象数据（U、T、H）代入文中基于基本环境参数的导线覆冰预测模型，由于时间跨度大，导线存在结冰和融冰的反复过程，因此文中只将覆冰速率的变化趋势和光纤监测到的最大覆冰厚度进行对比，得到对比结果如图9所示。可以看到：

1）在本次覆冰期内，光纤传感器监测到4个覆冰厚度峰值点No.1～No.4，具体覆冰厚度差异为：No.3>No.2>No.1>No.4。根据环境参数所获得的覆冰速率在4个点处的数值分别为4.05、4.48、10.89、3.51 mm/h，数值大小差异和监测结果相吻合。

2）在未监测到覆冰厚度的时间段内，预测模型所获得的覆冰速率值为零或接近于零的极小值。

根据上述2点，可认为在长时间范围内的文中模型所得线路覆冰速率预测趋势和实际观测结果是相吻合的。

为进一步验证文中模型的精度，另选取了2021年初渝东地区某输电线路B在短时间内的一个连续覆冰期进行对比分析，结果如图10所示。

根据图10（a）可知，光纤监测到线路B在18日零时达到最大覆冰厚度12.8 mm，文中模型的预测值则从1月17日15时开始增加，在18日2时达到最大值13.6 mm，相对误差为6.6%。且该结果和视频监测的覆冰图像（图10（b））相对应，由于气温升高，线路从18号凌晨2时—3时开始融冰，至18日清晨，线路覆冰全部融化，模型在该时段内得到的覆冰速率为零，进一步证实了预测值的准确性。

3 结 论

传统输电线路覆冰预测模型基于包括水滴中值体积直径和空气液态水含量在内的4项环境参数，涉及流体力学和热力学计算，环境参数获取较为困难，计算过程复杂，制约了架空输电线路覆冰实时预测。

1） 4项覆冰环境参数对输电线路覆冰速率的影响并不完全独立，dMVD和w对覆冰速率的影响程度受到风速和温度的控制，在风速较大、温度接近0 ℃时（严重覆冰发生的条件），dMVD和w对覆冰速率的影响程度是较小的，这为建立基于更少环境参数的导线覆冰模型奠定了基础。

2） 在大量数值模拟的基础上，通过基于粒子群算法的BP神经网络建立起了4项环境参数（U，T，dMVD，w）和导线覆冰速率的映射关系NET-1，模型平均误差为0.39 g/min，规避了传统覆冰导线覆冰模型在流场和热力学上的复杂计算过程。

3） 基于4项环境参数对导线覆冰速率影响的非独立性，构建了风速U、温度T和相对湿度H三项环境参数与不同获得的环境参数dMVD和w的拟合关系式，建立了基于3项基本环境参数的导线覆冰预测模型，模型准确度达6.6%。

参考文献

［1］  毕聪来， 蒋兴良， 韩兴波， 等. 采用扩径导线替代分裂导线的防冰方法[J]. 电工技术学报， 2020， 35（11）： 2469-2477.

Bi C L， Jiang X L， Han X B， et al. Anti-icing method of using expanded diameter conductor to replace bundle conductor[J]. Transactions of China Electrotechnical Society， 2020， 35（11）： 2469-2477.（in Chinese）

［2］  蒋兴良， 张志劲， 胡琴， 等. 再次面临电网冰雪灾害的反思与思考[J]. 高电压技术， 2018， 44（2）： 463-469.

Jiang X L， Zhang Z J， Hu Q， et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering， 2018， 44（2）： 463-469.（in Chinese）

［3］  Finstad K J， Lozowski E P， Gates E M. A computational investigation of water droplet trajectories[J]. Journal of Atmospheric and Oceanic Technology， 1988， 5（1）： 160-170.

［4］  Cansdale J T， Mcaaughton， I I. Calculation of surface temperature and ice accretion rate in a mixed water droplet/ice crystal cloud[R]. Royal Aircraft Establishment Technique Report， 1977.

［5］  Jones K F. A simple model for freezing rain ice loads[J]. Atmospheric Research， 1998， 46（1/2）： 87-97.

［6］  Makkonen L. A model of icicle growth[J]. Journal of Glaciology， 1988， 34（116）： 64-70.

［7］  Makkonen L. Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology， 1984， 23（6）： 929-939.

［8］  Makkonen L. Models for the growth of rime， glaze， icicles and wet snow on structures[J]. Philosophical Transactions of the Royal Society of London Series A： Mathematical， Physical and Engineering Sciences， 2000， 358（1776）： 2913-2939.

［9］  何高輝， 胡琴， 杜茗茗， 等. 自然覆冰导线直流电晕损失及其可听噪声特性实验研究[J]. 中国电机工程学报， 2022， 42（12）： 4633-4641.

He G H， Hu Q， Du M M， et al. Experimental research on the DC corona loss and audible noise characteristics of natural icing conductor[J]. Proceedings of the CSEE， 2022， 42（12）： 4633-4641.（in Chinese）

［10］  金海云， 聂诗超， 仝程， 等. 超疏水铝导线防覆冰机理研究[J]. 中国电机工程学报， 2017， 37（S1）： 204-210.

Jin H Y， Nie S C， Tong C， et al. Investigation on anti-icing mechanism of super-hydrophobic aluminum wire[J]. Proceedings of the CSEE， 2017， 37（S1）： 204-210.（in Chinese）

［11］  郭昊， 刘沛清， 屈秋林， 等. 输电线雾凇覆冰的工程估算方法[J]. 高电压技术， 2011， 37（4）： 1041-1049.

Guo H， Liu P Q， Qu Q L， et al. Estimation engineering method of rime accretion process on transmission lines[J]. High Voltage Engineering， 2011， 37（4）： 1041-1049.（in Chinese）

［12］  刘春城， 刘佼. 输电线路导线覆冰机理及雨凇覆冰模型[J]. 高电压技术， 2011， 37（1）： 241-248.

Liu C C， Liu J. Ice accretion mechanism and glaze loads model on wires of power transmission lines[J]. High Voltage Engineering， 2011， 37（1）： 241-248.（in Chinese）

［13］  蒋兴良， 姜方义， 汪泉霖， 等. 基于最优时间步长模型的输电导线雾凇覆冰预测[J]. 电工技术学报， 2018， 33（18）： 4408-4418.

Jiang X L， Jiang F Y， Wang Q L， et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society， 2018， 33（18）： 4408-4418.（in Chinese）

［14］  Zhang J， Makkonen L， He Q. A 2D numerical study on the effect of conductor shape on icing collision efficiency[J]. Cold Regions Science and Technology， 2017， 143： 52-58.

［15］  何青， 李军辉， 邓梦妍， 等. 架空输电导线覆冰冻结系数计算及其影响因素分析[J]. 电工技术学报， 2019， 34（19）： 4162-4169.

He Q， Li J H， Deng M Y， et al. Calculation and influencing factors of icing freezing coefficient of overhead transmission line[J]. Transactions of China Electrotechnical Society， 2019， 34（19）： 4162-4169.（in Chinese）

［16］  He Q， Zhang J， Deng M Y， et al. Rime icing on bundled conductors[J]. Cold Regions Science and Technology， 2019， 158： 230-236.

［17］  梁曦东， 李雨佳， 张轶博， 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术， 2014， 40（2）： 336-343.

Liang X D， Li Y J， Zhang Y B， et al. Time-dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering， 2014， 40（2）： 336-343.（in Chinese）

［18］  王强， 楼文娟， 徐海巍， 等. 考虑时变气象参数的输电导线覆冰数值仿真[J]. 哈尔滨工業大学学报， 2022， 54（11）： 11-21.

Wang Q， Lou W J， Xu H W， et al. Numerical simulation of transmission line icing considering time-varying meteorological parameters[J]. Journal of Harbin Institute of Technology， 2022， 54（11）： 11-21.（in Chinese）

［19］  韩兴波， 蒋兴良， 毕聪来， 等. 基于分散型旋转圆导体的覆冰参数预测[J]. 电工技术学报， 2019， 34（5）： 1096-1105.

Han X B， Jiang X L， Bi C L， et al. Prediction of icing environment parameters based on decentralized rotating conductors[J]. Transactions of China Electrotechnical Society， 2019， 34（5）： 1096-1105.（in Chinese）

［20］  Makkonen L， Zhang J， Karlsson T， et al. Modelling the growth of large rime ice accretions[J]. Cold Regions Science and Technology， 2018， 151： 133-137.

［21］  杨茂， 王金鑫. 考虑可再生能源出力不确定的孤岛型微电网优化调度[J]. 中国电机工程学报， 2021， 41（3）： 973-985.

Yang M， Wang J X. Optimal scheduling of islanded microgrid considering uncertain output of renewable energy[J]. Proceedings of the CSEE， 2021， 41（3）： 973-985.（in Chinese）

［22］  Fu P. Modelling and simulation of the ice accretion process on fixed or rotating cylindrical objects by the boundary element method[D]. Quebec， Canada： Quebec University， 2004.