基于GA-XGBoost模型对社会消费品零售总额的影响因素分析

张歌 乔敏 刘晓慧

摘 要：随着我国经济转变为高质量发展，社会消费品零售总额作为体现我国当前内需的关键指标，研究其影响因素及未来趋势依旧是消费领域的关键问题。本文以社会消费品零售总额为因变量，从消费需求、商品供给、货币金融、消费环境和交通运输五大方面选取12个指标作为研究自变量，构建XGBoost回归与SHAP模型对因变量进行分析，以及GA-XGBoost回归模型进行预测。研究发现：（1）货币和准货币供应量期末值、国内生产总值、货币供应量期末值、固定资产投资额累计增长率、国家财政收入、国家财政支出等对社会消费品零售总额影响最大；（2）除了固定资产投资额累计增长率对社会消费品零售额是负向影响外，其他五个均对社会消费品零售额是正向影响。本文以机器学习、遗传算法、可解释方法等理论模型解释了影响社会消费品零售总额的几大因素，为研究经济领域影响因素拓展了新的模型研究方法，并根据实证分析为我国经济发展提供了相应的建议，以供参考。

关键词：社会消费品零售总额；GA-XGBoost回归模型；SHAP；消费需求；交通运输

本文索引：张歌，乔敏，刘晓慧.基于GA-XGBoost模型对社会消费品零售总额的影响因素分析[J].中国商论，2023（24）：-014.

中图分类号：F724 文献标识码：A 文章编号：2096-0298（2023）12（b）--04

1 研究意义

如果一个国家的人口数量差距较小，社会消费品零售总额较高，就意味著这个国家的经济发展较为稳定和成熟，也表明该国居民的收入水平较高、消费能力较强、经济增长潜力较大。因此，本文对社会居民和社会集团的消费水平的观察、研究、分析，对处在经济结构转换时期的经济发展有非常重要的必要性和可行性。

2 社会消费品零售总额现状分析

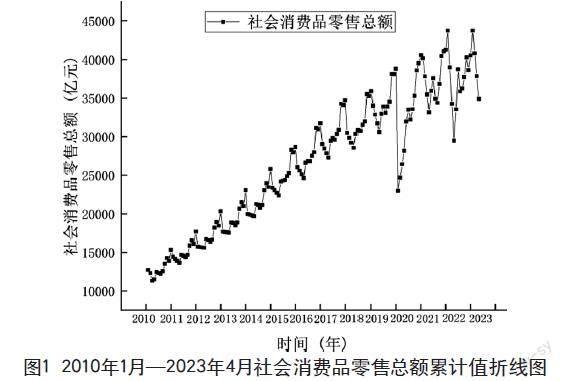
根据国家统计局规定，社会消费品零售总额累计值（亿元）是将1、2月数值进行累积，至2月发布1、2月的零售额总和。由于1月数据不能通过官方途径直接获得，便对研究年份中的1、2月社会消费品零售总额进行插补，2010—2023年的社会消费品零售总额变化趋势如图1所示。由图1可知，我国社会消费品零售总额有趋势性、季节性和随机性的特点。整体来看，我国社会消费品零售总额呈逐年增长态势，这与党的十八大以来坚定实施的扩大内需战略息息相关，我国经济持续向好发展。

3 数据来源及预处理

3.1 数据来源

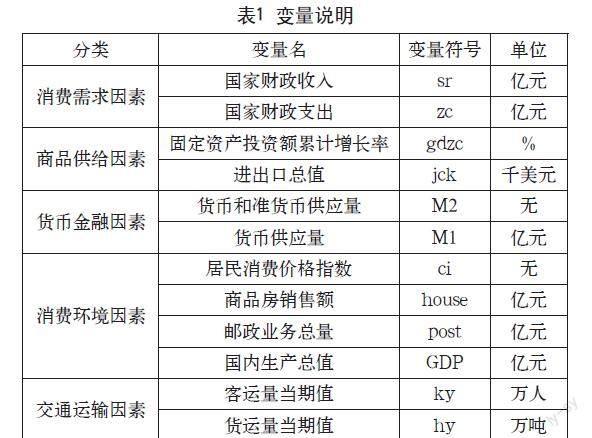
本文所用数据来源于国家统计局，具有可信度，研究对象为社会消费品零售总额，因此将其设为因变量。另外，从以下五个方面分别选取12个变量作为本文的自变量，表1是对各变量进行详细介绍和说明。

图1 2010年1月—2023年4月社会消费品零售总额累计值折线图

3.2 数据预处理

本文数据集中有两个指标需要对其进行缺失值插补，分别是按季度划分的国内生产总值数据和居民消费价格指数。本文采用插值法填充：分段线性插值、临近插值、球面插值和三次多项式插值这四种方法进行数据插补。其中，使用分段线性插值法计算x点的插值时，只用到x左右的两个节点，计算量与节点个数n无关，则在和这两个节点之间的一次线性方程为：

这四种插值方法都能较好地进行缺失值处理，简易起见，最终选择分段线性插值的方法得到完整的时序数据。

4 研究模型与方法

4.1 XGBoost模型

XGBoost采用集成的思想来提高预测精度，其目标函数可写成以下形式：

将上述目标函数进行最小化，其结果为：

综上所述，利用XGBoost进行特征选择，原理是在最优化目标函数后得到解释每个特征相对重要性的增益指标，增益越高，意味着特征对生成预测结果更重要。增益指标Gain的表达式如下：

4.2 SHAP模型

对于复杂模型，不能用模型本身来作解释，相反，必须使用一个简单的、可以被解释的模型，将其定义为原模型的任意解释逼近。SHAP将Shapley值解释为一种可加特征归因方法：

其中，G是解释模型；表示相应特征是否能被观察到，M是输入特征的数目；是每个特征的归因值；是模型的常数。由于树模型的输入必须是结构化数据，对实例应是所有值为1的向量，即所有特征均能被观察到，该公式简化为：

4.3 GA模型

遗传算法的步骤如下：

随机产生确定长度的n个染色体，，作为初始种群。

假设适应度函数为，则对所有的个体计算其相对应的值为：。根据设定的终止条件判断是否达到收敛状态，以选择下一步操作。选择适应度值大的个体进行交叉运算，则每个个体的选择概率为：

以选择概率为新的概率分布，从当前种群中选择个体重组新的个体种群：

随机从种群中选择两个不同的个体，以概率进行交换基因，得到新的两个个体，进行次1，得到一个新的种群。

从种群中随机选择个体，以变异概率进行变异，得到新的种群，这个群体作为完成一次遗传操作的子种群，即，此时传到适应度计算。

5 实证分析

5.1 机器学习回归模型选择

本文构建了机器学习回归模型中的四种：线性回归模型、KNN、XGBoost、CatBoost，表2列出了本文采用的四种方法在不同折数据之间的比较结果，包括五次重复实验的准确率。

其中，XGBoost回归模型的准确率最好，CatBoost模型最高准确率可达87.1%。综合选用XGBoost回归预测及可解释模型对社会消费品零售总额的影响因素进行分析研究。

5.2 社会消费品零售总额的影响因素

5.2.1 SHAP值的特征重要性

根據图3，横坐标是SHAP值，即各变量特征对模型输出的影响，纵坐标是不同的特征，颜色越红（深），特征值越大，越蓝（浅）则特征值越小。

由图3可以直观看到，货币和准货币供应量期末值、国内生产总值、货币供应量期末值、固定资产投资额累计增长率、国家财政收入、国家财政支出的特征重要性很高，是影响社会消费品零售总额最重要的六个特征变量。

图3 各特征的数值大小与各特征的SHAP值关系图

分析得出：货币和准货币供应量期末值、国内生产总值、货币供应量期末值、国家财政收入、国家财政支出、客运量当期值、进出口总值越大，社会消费品零售总额越大；邮政业务总量越不靠近均值、商品房销售额越靠近均值，社会消费品零售总额越大；固定资产投资额累计增长率、货运量当期值越小，社会消费品零售总额越大。

5.2.2 对多个变量的交互分析

图4是对SHAP值特征重要性占比最大的四个变量特征的交互分析，对两个变量特征交互图的分析如图4～图6所示。

（1）由图5可知，从左向右看，随着国内生产总值、国内生产总值SHAP值的增加，社会消费品零售总额越来越大。

（2）由图6可知，从左向右看，随着货币和准货币供应量期末值、货币和准货币供应量期末值SHAP值的增加，社会消费品零售总额越来越大。

（3）由图7可知，从左向右看，随着货币供应量期末值、货币供应量期末值SHAP值的增加，社会消费品零售总额越来越大。

5.3 GA-XGBoost模型预测

5.3.1 GA-XGBoost模型的构建

本文选用XGBoost模型对社会消费品零售总额进行预测，利用遗传算法GA找出XGBoost模型的最优参数，以及最优参数组对应的Best RSME，结果如表3所示。

5.3.2 利用GA-XGBoost模型预测

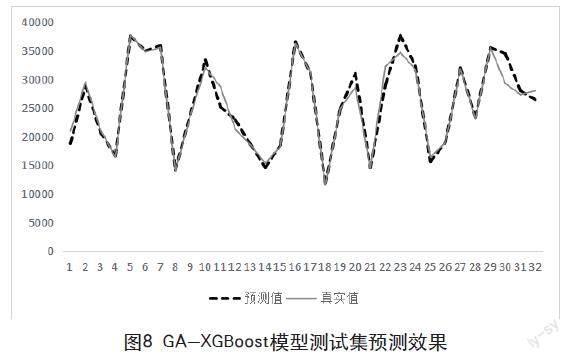
基于遗传算法参数寻优后的模型测试集预测结果如图8所示，深色线代表真实值，浅色线表示预测值，比较贴合，且GA-XGBoost模型准确率ACC高达95.68%，拟合较好，可以作为含有解释变量的模型对社会消费品零售总额进行预测，且预测效果较好。

6 结语

6.1 结论

本文研究社会消费品零售额的影响因素问题，通过模型对比选用XGBoost回归模型，得到前六个主要变量分别为货币和准货币供应量期末值、国内生产总值、货币供应量期末值、固定资产投资额累计增长率、国家财政收入、国家财政支出。分析可知，除了固定资产投资额累计增长率对社会消费品零售额是负向影响，其他五个均对社会消费品零售额是正向影响。

6.2 建议

针对上述分析和预测，本文提出提升我国消费的相关建议：

（1）实行开放的财政政策和宽松的货币政策；（2）积极推动互联网的发展；（3）加强房地产行业的宏观调控。

参考文献

王哲， 颜卫忠. 我国社会消费品零售总额预测方法与实证分析[J]. 环渤海经济瞭望， 2017（9）： 40-41.

李欣欣. 基于向量自回归的我国社会消费品零售总额预测分析[J]. 江苏商论， 2017（9）：3-8.

吴天魁， 王波， 周晓辉. 我国社会消费品零售总额的预测分析：基于最小二乘法的改进GM（1，1）模型[J].中国商贸， 2014（16）：83-84.

邓唯茹， 何跃， 蒲彦希. 社会消费品零售总额组合预测模型研究[J]. 统计与决策， 2014（4）：24-27.

罗中德， 赖美艳. 中国社会消费品零售总额的预测分析[J]. 统计与决策， 2013（2）：143-145.

秦伟良， 姚如一. 基于状态空间建模法的社会消费品零售总额预测[J]. 统计与决策， 2008（10）：16-18.

法丽娜. 关于我国社会消费品零售总额持续增长的实证分析[J]. 经济问题， 2010（5）：32-35.

方湖柳. 社会消费品零售总额波动规律及影响因素分析[J]. 山西财经大学学报， 2009， 31（7）： 22-28.

Ya ping Jiang. Prediction of the national total retail sales of consumer goods based on ARIMA model[C]. 4th International Conference on Advanced Education and Management， 2017， 28（2）： 13-14.

Peng yue Xu. Analysis and prediction of total retail sales of consumer goods based on multiple regression and S ARIMA model[C]. 2020 International Conference on Big Data Application& Economic Management， 2020， 32（2）：10-14.

Manago S Pan Y， Pohlen T. Hybrid Neural Network Model in U.S. Retail Sales[M]. Emerald Group Publishing Limited， 2013. Forecasting Aggregate.

Schmidt JR. Forecasting State Retail Sales： Econometric Vs. Time Series Models. Annals of Regional Science，1979，13（3）： 91.