基于极限平衡法的边坡三维稳定性计算

肖合伟

(江西省潦河工程管理局,江西 宜春 330700)

0 引言

边坡稳定性计算是边坡工程中重要的研究内容。稳定性计算关乎边坡稳定性状态及防护设计的相关内容,对于边坡的防护与治理具有重要现实意义。目前,关于边坡的稳定性计算主要包括理论分析法、模型实验法及数值模拟计算法。陈应显等[1]基于标准椭圆球,构建了含软弱夹层的三维边坡稳定性计算模型,推导了边坡稳定性计算理论,结果表明,含弱层边坡随着滑体宽度增加稳定性系数逐渐降低;王东等[2]基于极限平衡原理,研究了含顺倾弱层边坡的三维稳定性计算理论;结果表明,白音华一号露天煤矿非工作帮边坡稳定系数与弱层暴露长度呈负相关关系;朱大勇等[3]基于极限平衡条件,研究了对称边坡的三维稳定性计算方法,结果表明,初始正应力的假设与修正函数的选择对最终稳定系数结果的影响不大,采用文章提出的方法可以有效地对边坡的稳定性进行计算;张剑波等[4]依托黄土高边坡提出了一种三维稳定性计算方法,并与二维边坡稳定性计算进行了对比分析,结果表明,三维模型的计算精度优于二维稳定性计算模型;贺伟明等[5]基于Morgenstern-Price边坡稳定分析极限平衡法,研究了膨胀力作用对抗剪强度影响,结果表明,约束条件对膨胀力具有显著影响,当存在微小约束间隙时,膨胀力将明显降低;张坤勇等[6]基于极限平衡理论,研究了膨胀土边坡失稳机理,结果表明,膨胀土裂隙是影响边坡稳定性的关键因素。此外,在膨胀土边坡稳定性分析中,无需单独考虑膨胀作用影响。

考虑三维边坡稳定性计算的理论方法研究较少,本文基于极限平衡法理论,创新性地引入坡面荷载作用下的边坡三维计算模型,推导了在坡面荷载作用下边坡的三维稳定性计算模型,系统地研究了坡面荷载、土体抗剪强度和坡角等因素对边坡稳定性的影响。本文的计算可为边坡的稳定性计算提供理论依据。

1 边坡稳定性计算理论推导

假定存在一处于极限平衡状态的三维边坡。边坡具体的尺寸和形状如图1所示。在此基础上,建立对数螺旋锥面坐标系。假定土体的破坏准则为摩尔-库伦本构模型。边坡的高度、宽度和坡角分别用H(m)、B(m)和β(°)表示,土体的抗剪强度指标为内聚力c(kPa)和内摩擦角φ(°)。土体的容重为γ(kN/m3),坡面荷载为p(kN/m3)。边坡在坡面荷载作用下,滑体可视为绕坐标原点转动的刚体,滑动面形状可以由AC和A′C′确定(图1),对应的方程分别为:

(a)坐标系模型 (b)边坡计算模型

r=r0e(θ-θ0)tanφ

(1)

(2)

式中,φ为土体材料的内摩擦角,°;r为坐标原点到旋转中心的距离,m;θ为滑动面圆弧的半径与水平面之间的夹角,°。

通过原点与滑体的交线为圆弧,对应的半径可由下式计算得到:

(3)

螺旋锥面的中心轴线方程为:

(4)

根据功能原理,建立边坡在重力作用下运动所做的功为:

(5)

式中,γ为土体的重度,kN/m3;x1、x2、y和θB分别由下式计算得到:

(6)

(7)

(8)

(9)

(10)

(11)

根据摩尔-库伦屈服准则和塑性相关流动法则,得到边坡运动时塑性耗散能为:

(12)

式中,c为土体黏聚力,Pa;β为边坡的坡角,°。式(12)积分区域分别由(θ0,θB)及(θB,θh)组成。根据极限平衡原理,边坡坡面荷载对旋转中心转动的速率为:

(13)

当边坡滑体失稳并绕原点旋转时,坡面荷载做功,积分可得到边坡坡面荷载所做功为:

(14)

根据土体耗能量和坡面荷载能量等于土体重力势能。边坡稳定系数表示为:

(15)

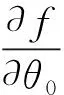
(16)

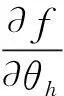
(17)

(18)

求解上面方程,可以得到三维边坡在坡面均布荷载作用下的稳定系数的最小值。

2 工程案例分析

为验证本文理论推导的正确性,进行工程案例具体验证。本文基于江西某典型红黏土边坡为分析对象,研究坡面荷载及坡角对边坡稳定性的影响。根据室内土工试验,研究边坡黏土的密度为14.5 g/cm3,颗粒比重为2.5,液限为59.4%,塑限为31.7%,液性指数为0.08,表现出硬塑的特性。该边坡的高为20 m,边坡的顶面长度为15 m,边坡高度为10 m,假定坡角和坡面荷载为变量。坡面荷载假定为均布荷载,进一步假定坡面荷载与内聚力的无量纲比值分别为0、0.2、0.4和0.6。边坡典型剖面见图2所示。

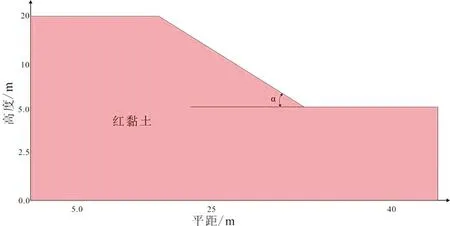
图2 边坡典型剖面

图3得到了边坡三维稳定性系数与内摩擦角的相互关系。结果表明,坡面无均布荷载和存在不同大小的荷载工况下,边坡的稳定性系数表现出相同的趋势,即边坡稳定性系数随内摩擦角的增大而增大,且内摩擦角越大,边坡稳定性系数增大速率越大。当无量纲坡面荷载为0,内摩擦角由0°增大至40°时,与坡面荷载与内聚力无量纲比值为0.2相比,边坡的稳定性系数增大了59%。导致这一现象的主要原因是由于随内摩擦角的增大,重力所做的功逐渐减小所造成的。

图4得到边坡了稳定系数与坡角的关系。结果表明,有无坡面荷载作用下,边坡的稳定性系数随坡角的变化规律基本相同。随坡角的增大,边坡稳定性系数逐渐减小。当坡角由50°增大至60°时,对应无量纲坡面荷载分别为0、0.2、0.4和0.6时,边坡的稳定性系数降低了25%、25.6%、26%和26.8%。当坡角由80°增大至90° 时,边坡的稳定性系数减小了15%、15.2%、15.5%和15.6%。

图4 稳定系数与坡角的关系

图5的得到了无量纲坡面荷载和边坡稳定系数的关系。首先假定无量纲坡面荷载分别为0、0.2、0.4和0.6,边坡的宽高比和土体内摩擦角分别为2.0和20°时,且边坡坡度由50°变化至80°,得到边坡稳定性系数与无量纲坡面荷载的关系。结果表明,在边坡坡角相等的基础上,当无量纲坡面荷载增加时,边坡稳定系数呈线性增大趋势;当坡面荷载相同时,随边坡坡角的增大,稳定性系数降低,且坡面荷载越大,稳定性系数变化梯度越大。

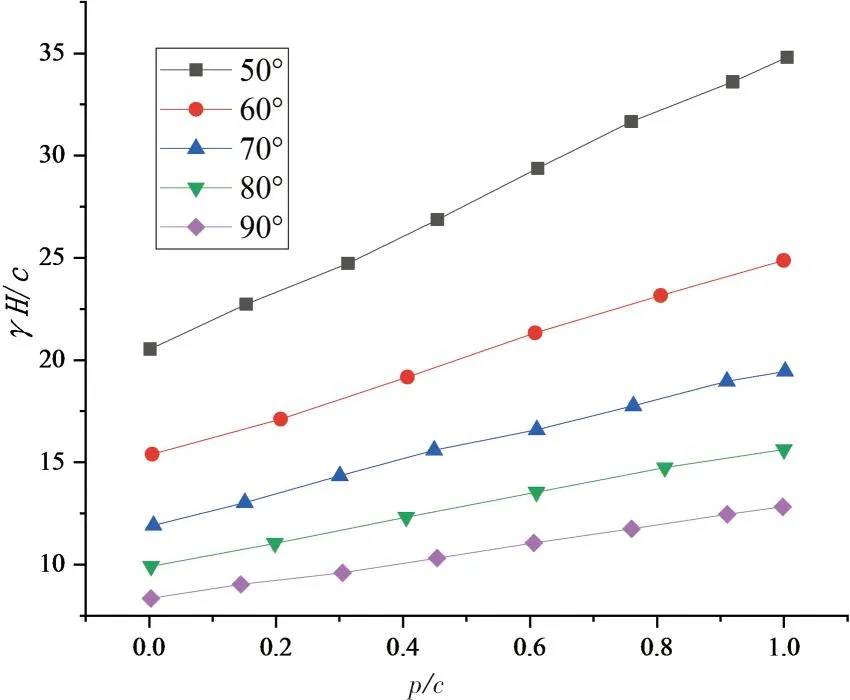
图5 稳定系数与无量纲坡面荷载的关系

图6汇总得到了边坡稳定系数与边坡宽高比的变化关系。其中坡角为70°,土体内摩擦角为20°。4条曲线分别对应于无量纲坡面荷载分别为0、0.2、0.4和0.6。结果表明,当边坡的宽高比小于2时,边坡的稳定性系数波动较大,当边坡宽高比大于2.0时,边坡稳定性系数变化较为平缓。因此,对于宽高比较小的边坡,稳定性系数波动较大,而对于宽高比较大的边坡,由于边坡的边界约束较小,因此采用二维计算与三维的结果差别较小。实际工程中当宽高比较小时,二维不可以替代三维计算。此外,根据计算结果,当边坡的宽高比从1.0增大至3.0,对应的无量纲坡面荷载分别为0、0.2、0.4和0.6时,边坡的稳定性系数降低比例分别为18%、17.3%、16.7%和16.1%。当边坡的宽高比从3.0增大至10.0,边坡的稳定性系数降低比例分别为12.5%、2.2%、2.0%和1.8%。

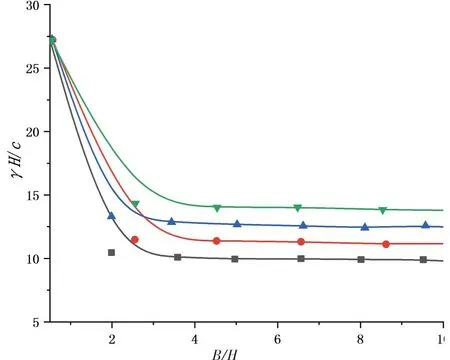
图6 稳定系数与坡面宽高比的关系

3 结论

本文基于极限平衡理论,建立了考虑坡面荷载的三维边坡稳定性计算模型,详细分析了土体抗剪强度、坡角、坡面荷载及边坡宽高比对边坡稳定性的具体影响。得到如下结论:

(1)坡面不存在荷载和存在大小不同荷载的工况下,边坡的稳定性系数表现出相同的趋势,即稳定系数随内摩擦角增大而增大,且内摩擦角越大,边坡稳定性系数增大速率越大。

(2)有无坡面荷载作用下,边坡的稳定性系数随坡角的变化规律基本相同。随坡角的增大,边坡稳定性系数逐渐减小。当坡角由50°增大至60°时,对应坡面荷载分别为0、0.2、0.4和0.6时,边坡的稳定性系数降低了25%、25.6%、26%和26.8%。当坡角由80°增大至90°时,边坡的稳定性系数减小了15%、15.2%、15.5%和15.6%。

(3)当无量纲坡面荷载增加时,边坡稳定系数呈线性增大趋势;当坡面荷载相同时,随边坡坡角的增大,稳定性系数降低,且坡面荷载越大,稳定性系数变化梯度越大。边坡的宽高比小于2.0时,稳定性系数波动较大,当边坡宽高比大于2.0时,边坡稳定性系数变化平缓。因此,对宽高比较小的边坡,二维稳定性计算不可以替代三维稳定性计算。