基于灵活编组的城市轨道交通大小交路优化
安 飞,刘亚苹,常秀娟,何 彬,李 欣,卜东一
(1.河北交通职业技术学院,河北 石家庄 050035;2.河北轨道运输职业技术学院,河北 石家庄 052165)
0 引言
截至2022年年底,我国城市轨道交通运营总里程已经突破1万km(10 287.45 km),在建线路总规模6 675.57 km,总体规模和建设速度都居世界第一。随着线路不断地由城市中心向外扩张,客流强度也呈现较大的不均衡性。固定编组、单一交路、固定停站的列车开行方案已经不能满足乘客的出行需求,存在乘客平均等待时间较长、部分区间运力虚弥的现象,造成乘客满意度较低和部分运营资源浪费。因此,探索灵活编组、大小交路等运营组织模式,合理配置资源,设计与客流相匹配的列车开行方案,从而减少乘客等待时长,提高列车满载率,将有助于地铁企业取得更好的经济效益和社会效益,同时有利于推动城市轨道交通双碳发展战略。
陈维亚等[1]从乘客、企业以及车站的候车人数比例方差之和3个方面建立目标函数,求解最小成本,并设计了智能算法进行模型求解。杨安安[2]以企业车辆使用成本、列车运营成本和乘客出行成本最小为目标,考虑跨线列车对线路通过能力的影响,以列车发车间隔、满载率、可用车辆数为约束,构建跨线运营模式下的运力配置模型。高毅[3]根据市域线的特点,对乘客和运营企业进行综合考虑,研究了快慢车和多交路结合运营方案。本文重点研究灵活编组时大小交路方案的优化,此研究能为城轨灵活编组列车大小交路运输组织工作提供一定的支撑和参考。
1 问题描述
如图1所示,某条城市轨道交通线路共N个车站,下行方向为车站1到N,上行反之。假设采用大小交路开行方案,大交路从车站1到N往返运行,编组数目为B2,发车频率为B2;小交路从折返站x到y往返运行,编组数目为B1,发车频率为F1,且大小交路列车成比例开行。在Q1区段,乘客可以乘坐大交路和小交路两种列车,在Q2区段,乘客只能乘坐大交路列车。
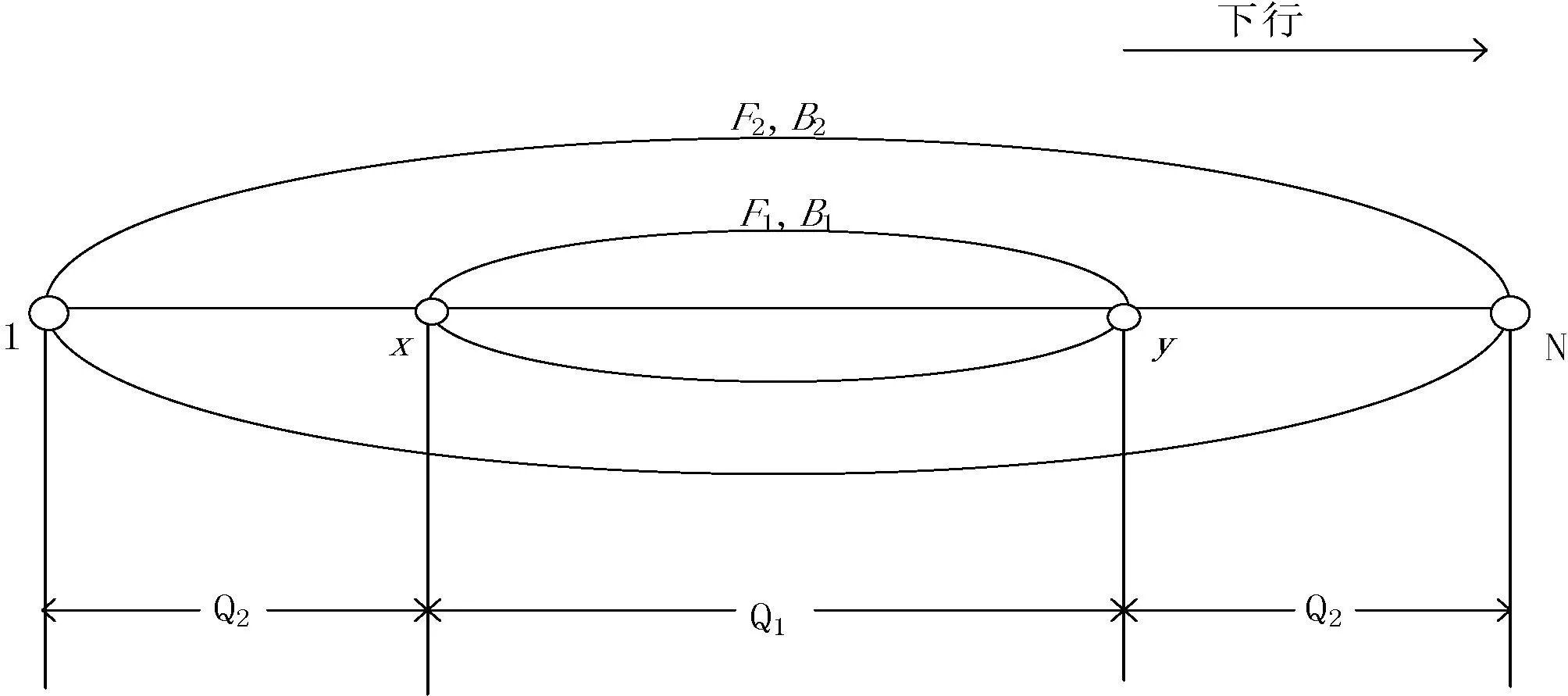
图1 城市轨道交通线路
本文以某城市轨道交通线路高峰时段为研究对象,已知相关客流数据及设备设施参数,在大小交路、灵活编组、站站停车形式下,在满足乘客需求、现有车底数、线路通过能力、断面满载率、编组数目、发车频率等约束下,确定该时段是否需要开行大小交路以及大小交路列车发车频率、开行大小交路时小交路折返站的位置和大小交路列车编组数目,使乘客出行成本、企业运营成本的综合目标最小,依据此来设定目标函数。
2 模型
基本假设:
(1)列车上行和下行开行数量一致,列车到每个车站均需停车。
(2)假定只有大小交路,不设置其他交路形式,且大小交路列车独立运用车底。
(3)假设站台候车的所有乘客在列车到站后都能够上车,而且乘客的时间价值相同。
(4)小交路列车折返时对大交路列车运行不产生影响。
(5)两个相邻车站上下行站间距、区间运行时分均相同,大小交路列车在每个站的上下行方向停站时间相同。
(6)不考虑编组解体而产生的附加费用。
2.1 参数定义
(1)i,j,m——车站索引,i,j,m∈{1,2,…,N};
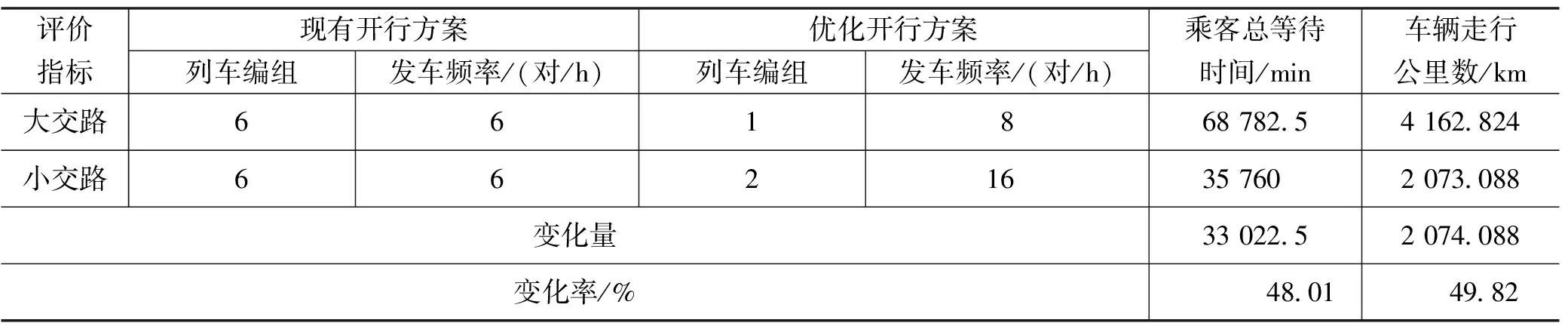
(2)x,y——下行起始站、终点站折返站索引,x (3)e(m,m+1)——区间索引,表示相邻两个车站的区间或断面; (4)c——上下行索引,c∈(1,2),1表示下行,2表示上行; (5)h——大小交路,h∈(1,2),1表示小交路,2表示大交路; (6)Oij——该小时从第i车站上车到第j车站下车的客流量,单位:人次; (7)Lm,m+1——第m车站中心到第m+1车站中心的站间距,单位:km; (8)Tm,m+1——区间e(m,m+1)的列车运行时分,单位:s; (10)Sm——第m站停站时分,单位:s; (12)U——一辆车的定员; (13)β——一列车满载率; (14)Bmax——现有列车的编组数目; (1)F1、F2——小、大交路的列车开行频率,单位:对/h; (2)B1、B2——小、大交路列车编组辆数,单位:辆; (3)x、y——小交路的起始、终到折返站。 目标函数考虑用乘客等待时间来表示乘客出行成本,用车辆总走行公里数来表示企业运营成本。 2.3.1 乘客等待时间 当列车行车间隔小于10 min时,可以用发车间隔的一半来表示整体客流的平均候车时间[4]。 (1) (2) minZ1=Ts+Tx (3) 式(1)是下行乘客总等待时间(min),式(2)是上行乘客总等待时间(min),式(3)是乘客总等待时间(min)。 2.3.2 车辆总走行公里数最小 (4) 将两个目标加以权重系数转化为单目标: minZ=min(λ1Z1+λ2Z2) (5) 式中,λ1为Z1的权重系数;λ2为Z2的权重系数。 根据世界银行给出的推荐值,非工作出行单位小时价值为人均小时工资收入的 0.3倍[5],故取 0.3 倍的人均工作小时工资收入作为单位候车时间成本。 (6) 式(7)~(11)是发车频率的限制,式(13)~(14)表示该时段的运输能力能够满足各断面客流的需求,式(12)是各断面客流的计算方法;式(15)是满载率满足条件限制,式(16)是列车编组数目限制,式(17)是小交路折返站的约束,式(18)是可用车底数约束。 (7) (8) (9) Fh∈N+,h=1,2 (10) (11) (12) max{De(m,m+1),c,1≤m≤x-1∪y≤m≤N-1,c=1,2}≤F2×U×B2×βmax (13) U×Bh×βmax (14) 0≤β≤1 (15) 1≤Bh≤Bmax (16) 1≤x≤y≤N (17) (18) 某线路自东向西共26个车站,25个区间。可以实现自动折返的车站有:1,7,14,21,23,26,各车站站间距L1,2…L25,26=1.064,1.316,1.174,3.607,1.403,1.404,1.030,1.195,1.622,1.285,2.345,0.810,1.270,1.441,1.146,0.898,0.876,0.984,1.267,0.862,1.083,1.156,1.337,1.220,1.290(km),各车站中心到折返线终点的长度均约为0.4 km,各区间运行时分T1,2…T25,26=91,101,100,221,108,105,89,95,122,102,165,77,102,107,95,80,84,85,105,80,91,94,103,95,102(s),各车站的停站时间S1…S26=45,40,40,35,35,35,45,30,35,40,40,35,40,40,40,40,40,45,40,40,55,35,40,35,35,45(s),如果小交路的起点和终点车站现在没有折返线,则需要重新铺设折返线,这样造价非常高。所以本文规定:目前不具备折返线的车站,其折返时间设置成∞,具备折返线的车站,其折返时间均为120 s。 该线路目前采用A型车,为了充分利用现有资源,节省成本,本文假定仍采用现有的A型车,其定员是310人,车底保有量是36列,现有列车编组数目是6。早高峰8:00—9:00的部分客流分布如表1所示。 表1 部分OD数据 该市2022年人均GDP为89 000元,人均年工作时间为2 091 h,将其带入式(6),计算得λ1=0.21元/min,单车运营成本为48元/km[6]。 则目标函数确定为: minZ=min(0.21Z1+48Z2) (19) 将相关参数数据带入模型,用Python软件求解。计算结果为:B1=2,B2=1,F1=16,F2=8,x=7,y=26。 优化后的与现有的开行方案的评价指标对比如表2所示。 表2 不同交路方案评价指标对比 经计算,该时段优化后的开行方案乘客总等待时间是35 760 min,现有的开行方案乘客总等待时间是68 782.5 min,减少了33 022.5 min,减少了48.01%;该时段优化后的开行方案车辆走行公里数是4 162.824 km,现有的开行方案车辆走行公里数是2 073.088 km,减少了2 074.088 km,减少了49.82%。说明优化的列车开行方案不管是乘客出行成本还是企业运营成本都大大降低了,不仅可以提升乘客服务水平,还能有效降低城市轨道交通公司的运营成本。 本文以某条城市轨道交通线路高峰期为研究对象,综合考虑乘客和企业的利益,建立了列车开行方案优化模型。将客流OD分布表及相关参数输入模型,可以计算出当前条件下的最优列车开行方案。 本文以某条地铁线路为例,将优化的开行方案与现有的开行方案进行对比。结果表明优化后的方案目标函数更小,综合成本更低,验证了模型的可行性与正确性。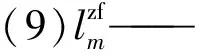


2.2 变量定义
2.3 目标函数

2.4 约束条件
3 案例分析
3.1 基本参数
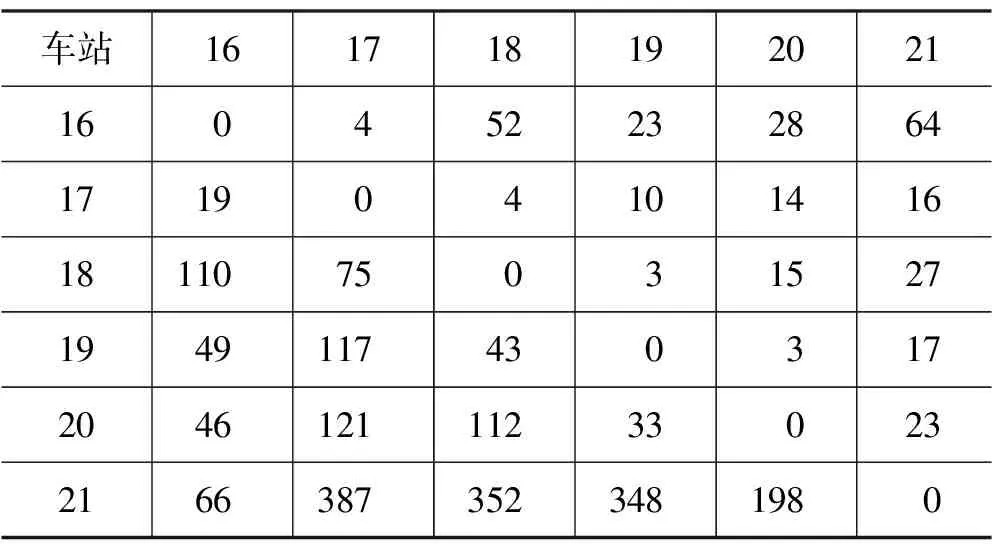
3.2 结果分析
4 结语
——国外课堂互动等待时间研究的现状与启示

