欠驱动VTOL飞行器的自耦PID控制方法

曾喆昭, 章禛昊

长沙理工大学电气与信息工程学院, 长沙 410014

0 引 言

VTOL飞行器因其起飞距离短和垂直起降的性能,因而在军用与民用领域都具有极其重要的作用,已经成为各国争相研究的飞行器对象.由于VTOL飞行器存在3个运动自由度却只有2个控制输入,因而是一个典型的欠驱动系统[1-3].对于控制量个数少于自由度个数的欠驱动系统而言,由于其具有重量轻、造价低、能耗小和灵活度强等特点,因而被广泛地应用于桥式起重机[4-6]、欠驱动船舶[7]、机器人[8]、无人机吊挂飞行系统[9]和四旋翼飞行器[10]等欠驱动系统.

VTOL飞行器已引起了国内外控制领域学者的广泛关注[11-17].迄今为止,有关VTOL飞行器的控制方法主要包括如下几类:状态反馈控制方法[1-2]、反演控制方法[11-12]、动态面控制方法[3,13]、滑模控制方法[14-17]以及逆最优反馈控制[18]、双闭环PID控制[19]和非线性信息融合控制方法[20]等,都获得了有效的控制结果.然而,状态反馈控制方法存在动态品质与稳态性能欠佳的局限性;反演控制方法存在“微分爆炸”的局限性;动态面控制、滑模控制、逆最优反馈控制以及非线性信息融合控制等控制方法均存在结构复杂、计算量大的局限性;而双闭环PID控制方法则存在增益鲁棒性差与抗扰动鲁棒性差的局限性.

为了解决现有控制方法存在的各种局限性问题, 本文根据文献[21-24]提出了欠驱动VTOL飞行器的ACPID控制理论方法.

1 问题背景

1.1 VTOL飞行器模型

图1是VTOL飞行器的悬停示意图.

根据文献[20],VTOL飞行器的动力学模型可表示为

(1)

其中,状态变量y、z和θ分别是VTOL飞行器质心在参考坐标中的横、纵向位置与滚转姿态角,m和J分别是飞行器的质量和沿纵向轴的转动惯量,g为重力加速度,控制输入ut与um分别是底部垂向推力与滚转力矩,ε0是滚转力矩对横向与纵向运动的耦合作用系数.

由于VTOL飞行器(1)有3个自由度y、z和θ,却只有2个控制输入ut与um, 因而是一类典型的欠驱动非线性耦合系统.

(2)

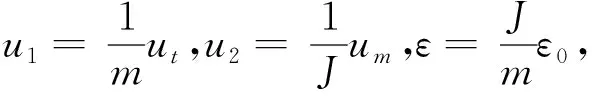
(3)

1.2 VTOL飞行器模型映射

对系统(3)做如下坐标变换:

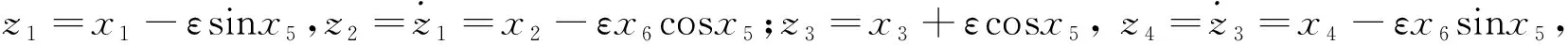
(4)

显然,上述坐标变换不仅使新的VTOL飞行器系统(4)实现了输入解耦的作用,而且使VTOL飞行器系统(3)的不稳定质心位置(x1,x3)映射到具有平坦输出的Huygens振动中心(z1,z3).由于新的VTOL飞行器系统(4)的输出是平坦的(z1与z3均不受u2的影响),因而有效避免了非最小相位VTOL飞行器零动态不稳定的问题.由于系统(4)与系统(3)或系统(2)是等价映射,因此由VTOL飞行器系统(4)设计的控制器u1和u2可以实现对系统(3)或系统(2)的有效控制.

2 欠驱动VTOL飞行器控制系统设计

2.1 VTOL飞行器的基本控制原理

为了便于分析,分别设uy与uz2个虚拟控制器为

(5)

(6)

则VTOL飞行器系统(4)可简化为式(7)的形式

(7)

根据式(5)与式(6),可得u1和x5分别如下:

(8)

x5=-arctan(uy/uz)

(9)

显然,只要设计好横纵向位置的控制器uy与uz,即可获得控制力u1,从而获得VTOL飞行器底部垂向推力ut=mu1.如果设滚转姿态角虚拟指令为

x5r=-arctan(uy/uz)

(10)

则可设计VTOL飞行器滚转姿态角控制器u2,进而获得滚转力矩um=Ju2.

2.2 VTOL飞行器垂向推力控制器设计

设VTOL飞行器质心坐标的期望轨迹为x1d与x3d,并设期望滚转姿态角为x5d=θd=0,从而可得Huygens振动中心坐标的期望轨迹为

z1d=x1d-εsinx5d=x1d

(11)

z3d=x3d+εcosx5d=x3d+ε

(12)

(1) 横向位置控制器设计

设横向位置跟踪误差为

e11=z1d-z1

(13)

其中,z1d=x1d,z1=x1-εsinx5.

(14)

在忽略积分环节的情况下,根据文献[21],可设计横向位置的ACPDy控制器为

(15)

其中,zcy>0是ACPDy控制器的速度因子.

(2)纵向位置控制器设计

设纵向位置跟踪误差为

e31=z3d-z3

(16)

其中,z3d=x3d+ε,z3=x3+εcosx5.

(17)

在忽略积分环节的情况下, 根据文献[21],可设计纵向位置的ACPDz控制器为

(18)

其中,zcz>0是ACPDz控制器的速度因子,g是重力加速度.

根据式(15)与式(18)分别获得横纵向位置控制器uy与uz后,根据式(8)即可获得控制力u1为

(19)

进而可获得欠驱动VTOL飞行器底部垂向推力为ut=mu1.

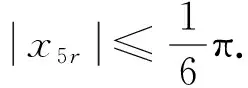
2.3 VTOL飞行器姿态角控制器设计

根据横纵向位置控制力获得VTOL飞行器姿态角虚拟指令x5r后,设滚转姿态角跟踪误差为

e51=x5r-x5

(20)

(21)

在忽略积分环节的情况下,根据文献[21],可设计滚转姿态角ACPD2控制器为

(22)

其中,zc2>0是ACPD2控制器的速度因子.

由式(22)即可获得欠驱动VTOL飞行器的滚转力矩为um=Ju2.

2.4 闭环控制系统分析

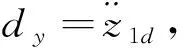
证明.将式(15)定义的横向位置控制力uy代入受控误差系统(14),可得横向位置闭环控制系统如下:

(23)

对系统(23)取拉普拉斯变换,并整理得

(24)

定义横向位置控制系统的传输函数为

(25)

当zcy>0时,由于Hy(s)在复频域的左半平面有双重实极点sp=-zcy<0,因而系统(23)或(25)是稳定的.又因为速度因子zcy与系统模型无关,因而系统(23)或(25)是鲁棒稳定的.

由系统(25),可得单位冲激响应为

hy(t)=texp(-zcyt),t>0

(26)

因而闭环系统(24)的时域解可表示为

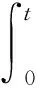
(27)

其中,“*”表示卷积积分运算.

当|dy|≤εy时,则有

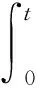
(28)

因而稳态误差可表示为

(29)

由式(26)可知, 当t≥0时,hy(t)≥0,因而有

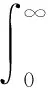
(30)

以上理论分析表明:稳态误差与速度因子的平方成反比,因而增大速度因子有利于提高稳态控制精度,增强抗扰动能力,具有重要的理论意义.

为了节省篇幅,欠驱动VTOL飞行器的纵向位置控制系统和滚转姿态角控制系统的分析不再赘述,可参照定理1进行鲁棒稳定性分析.

2.5 自适应速度因子

考虑到误差微分的敏感特性,定义ACPDy、ACPDz和ACPD2等3个自耦PD控制器的ASF (adaptive speed factor)模型分别为

zcy=zcmyexp(-β|e12|)

(31)

zcz=zcmzexp(-β|e32|)

(32)

zc2=zcm2exp(-|e52|)

(33)

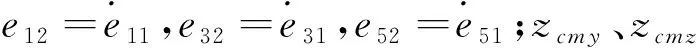
考虑到横纵向位置可以以相同的速度运行,因而其控制器的最小速度因子可以相同,即

zcmy=zcmz=20α/tr

(34)

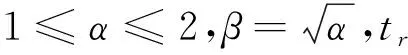
再考虑到内环的滚转姿态角虚拟指令是由外环横纵向控制力形成的,即x5r=-arctan(uy/uz),因此,要求滚转姿态角控制器ACPD2的最小速度因子zcm2应该满足如下不等式条件:

4zcmy≤zcm2≤10zcmy

(35)

3 仿真验证与分析

为了验证本文控制方法的有效性, 并与文献[20]进行比较分析,欠驱动VTOL飞行器的相关参数与文献[20]完全相同:飞行器质量m=5×104kg,耦合系数ε0=0.05,转动惯量J=2×105kg·m2.

设采样频率fs=1 000 Hz,重力加速度g=9.8 m·s-2,Huygens振动中心坐标为z1=x1-εsinx5,z3=x3+εcosx5.

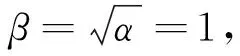
(1)ACPDy控制器

其中,zcy=10e(-|e12|).

(2)ACPDz控制器

其中,zcz=10e(-|e32|).

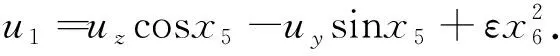
(3)ACPD2控制器

其中,zc2=80e(-|e52|),且|x5r|≤0.3 rad.

考虑到输入受限情况,要求|u2|≤80,进而可获得欠驱动VTOL飞行器的滚转力矩um=Ju2.

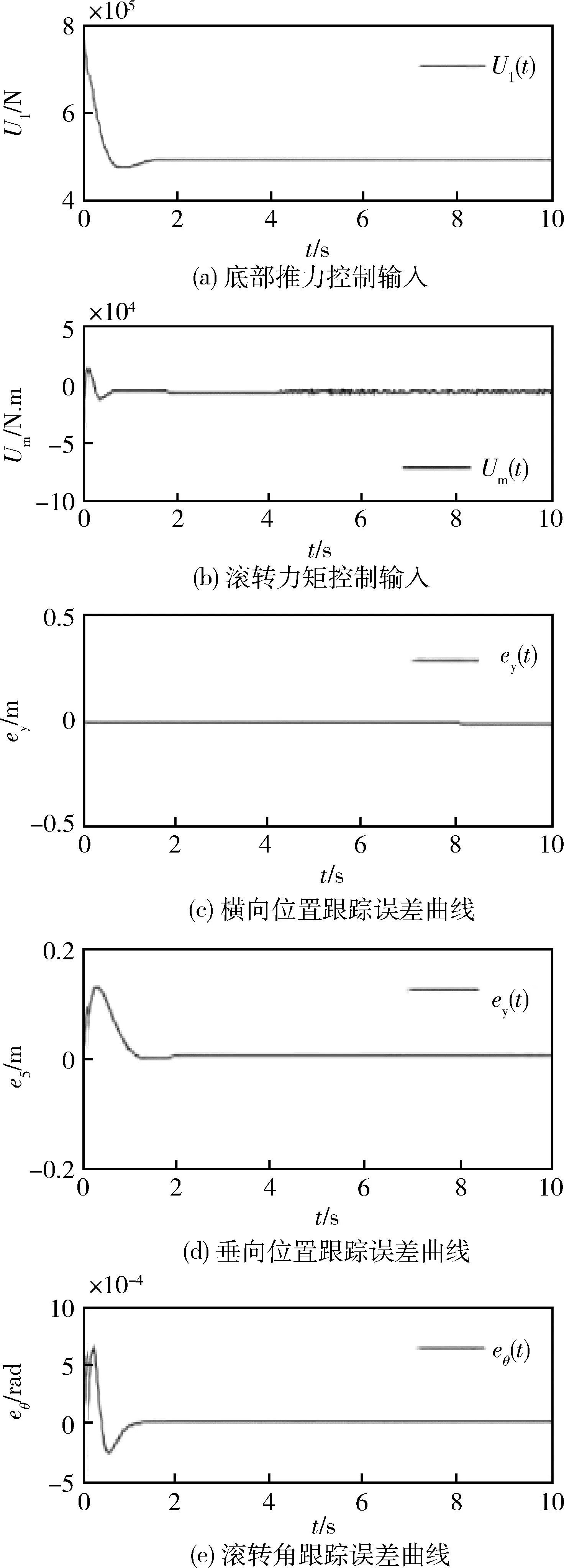
图3 文献[20]控制结果Fig.3 The control results in [20]

比较图2与图3可知,本文控制方法只需要6 s即可稳定在指定位置,而文献[20]则需要至少10 s才能实现稳定跟踪(由于文献[20]使用x3d=t来对纵向期望位置安排过渡过程,因而需要10 s才能达到期望的10 m,而本文则使用x3d=10 m,无需对纵向期望位置安排过渡过程),表明本文控制方法的响应速度是文献[20]的1.6倍以上.此外,本文控制方法的最大底部推力小于6×105N,而文献[20]则需要8×105N,表明本文控制方法的最大底部推力只需要文献[20]的75%即可.在姿态控制方面,本文控制方法不存在晃动现象,而文献[20]存在明显的晃动现象.由于文献[20]是基于系统模型的控制方法,且涉及偏导数计算、矩阵代数计算及其重复迭代计算,因而计算复杂、量大,不便于实际应用,而本文控制方法的每个控制器只涉一个速度因子,且与被控系统的模型无关,表明本文控制方法具有良好的模型鲁棒性.由于本文控制方法结构简单、计算量小、物理概念明确、控制思路清晰,因而更便于实际应用.

由于仿真实验3.1只考虑了垂直起飞的情况,没有考虑悬停和着陆情况,为了验证本文控制方法的有效性,下面将进行垂直起飞、悬停与着陆等全工况过程的控制.

仿真实验3.2.设VTOL飞行器的横向期望轨迹为x1d=10 m,期望滚转姿态角x5d=0,纵向期望轨迹为

(36)

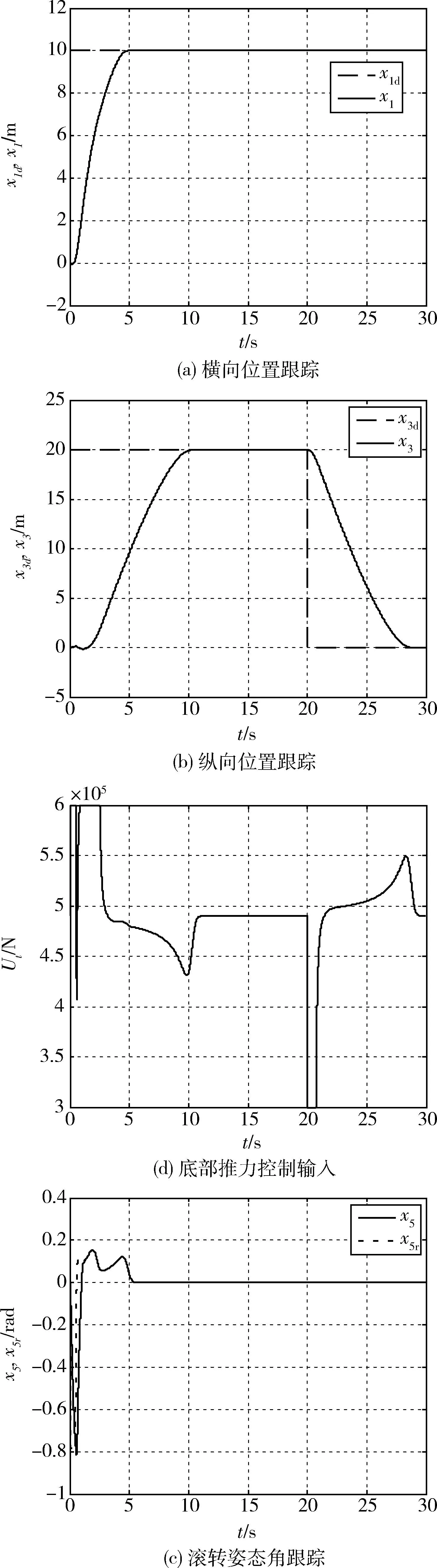
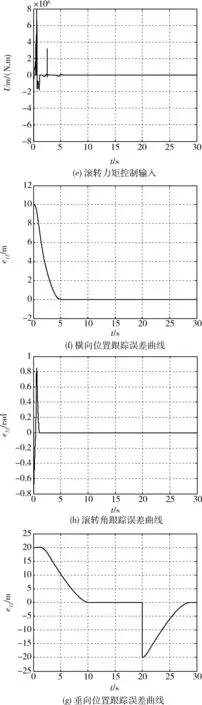
图4 垂直起飞、悬停与着陆控制结果Fig.4 Vertical take-off, hover and landing control results

由图4可知,本文控制方法对欠驱动VTOL飞行器垂直起飞、悬停与着陆等全工况过程进行控制, 都获得了良好的动态品质和稳态性能,横向与纵向位置分别在5 s与10 s之内即可进入稳定的控制状态,进一步表明了本文控制方法的有效性.由于文献[20]只考虑了垂直起飞的工况情况,没有考虑悬停与着陆的工况情况,因此无法进行比较分析.

4 结 论

针对欠驱动VTOL飞行器的控制问题,提出了一种自耦PID控制方法,在复频域分析了闭环控制系统的鲁棒稳定性,仿真结果表明了本文控制方法的有效性,不仅具有良好的动态品质和稳态性能, 而且控制系统结构简单、计算量小,便于实际应用.此外,本文控制方法的主要思想是根据横向与纵向2个虚拟位置控制器uy与uz作为外环控制,进而分别获得VTOL的底部推力和滚转姿态角的虚拟指令, 再根据滚转姿态角的虚拟指令,使欠驱动的VTOL系统映射为虚拟全驱动的VTOL系统,在欠驱动非线性系统控制领域具有重要的科学指导意义与广泛的应用价值.