在轨组装卫星自适应姿态控制
钱晓莱, 王瀚霆, 王小琰, 郭禹辰, 赵亚涛
1. 上海航天空间技术有限公司,上海 201109 2. 上海卫星工程研究所,上海 201109 3. 中国空间技术研究院通信与导航卫星总体部,北京 100098 4. 哈尔滨工业大学航天学院,哈尔滨 150001
0 引 言
随着科技的进步,人类对空间开发和应用的能力不断提高.受火箭推力、整流罩包络限制以及机构复杂程度的影响,当前可展式结构难以满足空间结构大跨度、大规模的发展趋势[1].通过将结构、功能基本单元依序组装,在轨组装技术可以很好地完成大型空间系统的构建和维护,具有结构效率高、扩展性强。可逐步升级等特性[2].
大型在轨组装卫星在组装过程中姿态控制系统任务复杂多变,组装完成后的系统质量参数未知,导致控制器承受质量参数不确定干扰,严重影响组装卫星的姿态控制精度.为了抑制参数不确定性干扰对姿态的影响,需开展抗扰动控制算法研究,如模型预测控制[3]、鲁棒H∞控制[4]和自抗扰控制[5]等.其中滑模控制因其具有强鲁棒性和易实现性等优势,而被广泛用于卫星的姿态控制领域[6-8].但在上述研究工作中系统状态渐近稳定,难以满足组装卫星对完成姿态机动任务的时间要求.因此,基于终端滑模面的有限时间滑模控制得到关注[9],状态收敛时间存在有限上界,该上界与状态初值相关,在状态初值未知时,难以对系统稳定时间进行判断.进一步,固定时间滑模控制能够解决稳定时间受状态初值影响的问题,具备更快的收敛速度和更强的鲁棒性,是当下的学术热点[10].
需要已知的干扰上界和系统颤振是滑模控制面临的两大问题.由于实际中的干扰大多未知,难以获取干扰上界,就需要较大的控制参数来保证系统稳定,导致控制系统能量损失严重并加重因控制不连续项而导致的滑模控制颤振问题[11].已有较多研究工作致力于解决上述问题,文献[12]设计了自适应律调节控制参数,结合边界层方法替代控制器中不连续项,实现干扰上界未知情形下的系统稳定;文献[13]设计了固定时间干扰观测器,通过对干扰的在线观测和补偿,提高控制精度的同时,减弱了颤振现象.但上述研究工作设置的仿真条件均过于理想,未考虑测量误差对控制结果的影响.
由姿态敏感器测量得到的卫星姿态、角速度信息带有含测量噪声、测量漂移在内的测量误差,会严重影响卫星的姿态精度和稳定度.为了提高在轨组装卫星的控制精度,结合组装卫星姿态敏感器冗余配置的特点,充分利用各敏感器间的互补性能,开展多敏感器信息融合算法研究,提高姿态确定精度是当下的学术热点[14].从融合结构角度出发,多敏感器信息融合主要分为集中式滤波和分散式滤波两种,其中集中式滤波对各敏感器信息进行统一数据处理,系统状态维数较大,存在计算负担大、容错能力较差等问题[15].因此,为了使信息融合算法具有故障容错能力,提高状态估计结果的可靠性,分散式滤波尤其是由Carlson提出的联邦滤波算法得到了广泛推广[16].
结合大型在轨组装卫星姿态敏感器冗余配置和质量参数未知的特点,为了抑制测量误差和参数不确定性干扰对组装卫星的影响,本文整合了陀螺/GPS导航子系统和陀螺/星敏导航子系统,建立联邦滤波体系求解状态全局最优估计,利用残差卡方检验方法实现对缓变故障、突变故障的检测、隔离和重构,提高姿态确定精度和结果可靠性.基于姿态估计结果,本文提出了一种新型的自适应固定时间滑模控制设计方法,通过参数辨识算法估计组装卫星的质量参数,提高滑模控制在干扰上界未知情形下的控制精度和自适应性,降低参数选取范围改善系统颤振.
1 大型在轨组装卫星的数学模型
大型在轨组装卫星结构如图1所示,卫星1经过在轨组装,与卫星2(组装对象)构成了组合体.图中红色圆盘代表卫星的对接环,每个卫星均采用3正装+1斜装的4反作用飞轮构型,卫星1配备陀螺/GPS导航子系统,卫星2配备陀螺/星敏导航子系统.
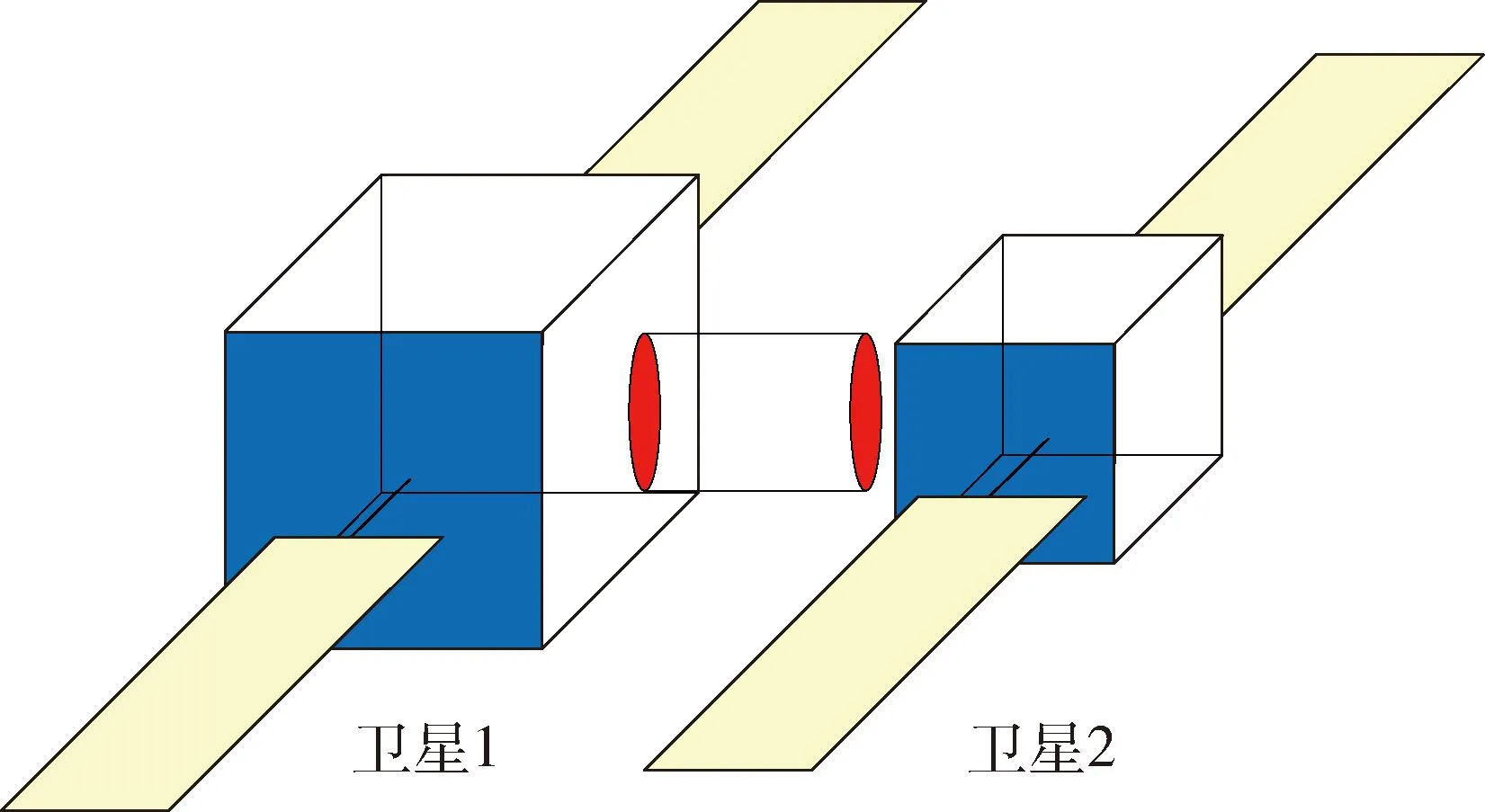
图1 在轨组装卫星示意图Fig.1 On-orbit assembled satellite schematic
为了便于分析,制定如下假设:
假设1.在轨组装卫星组合体之间为刚性连接,忽略相对姿态连接误差.
假设2.忽略太阳翼弹性振动导致的刚柔耦合干扰,忽略太阳翼相对卫星本体的转动.
在上述假设成立时,可将组装卫星视为一个带有飞轮的刚性卫星整体,后续推导使用的坐标系和矢量定义如图2所示.此外,记卫星1质心的绝对位置矢量为Xs,卫星2质心的绝对位置矢量为Xt,组装卫星系统质心指向卫星1质心的位置矢量为rs,组装卫星系统质心指向卫星2质心的位置矢量为rt.
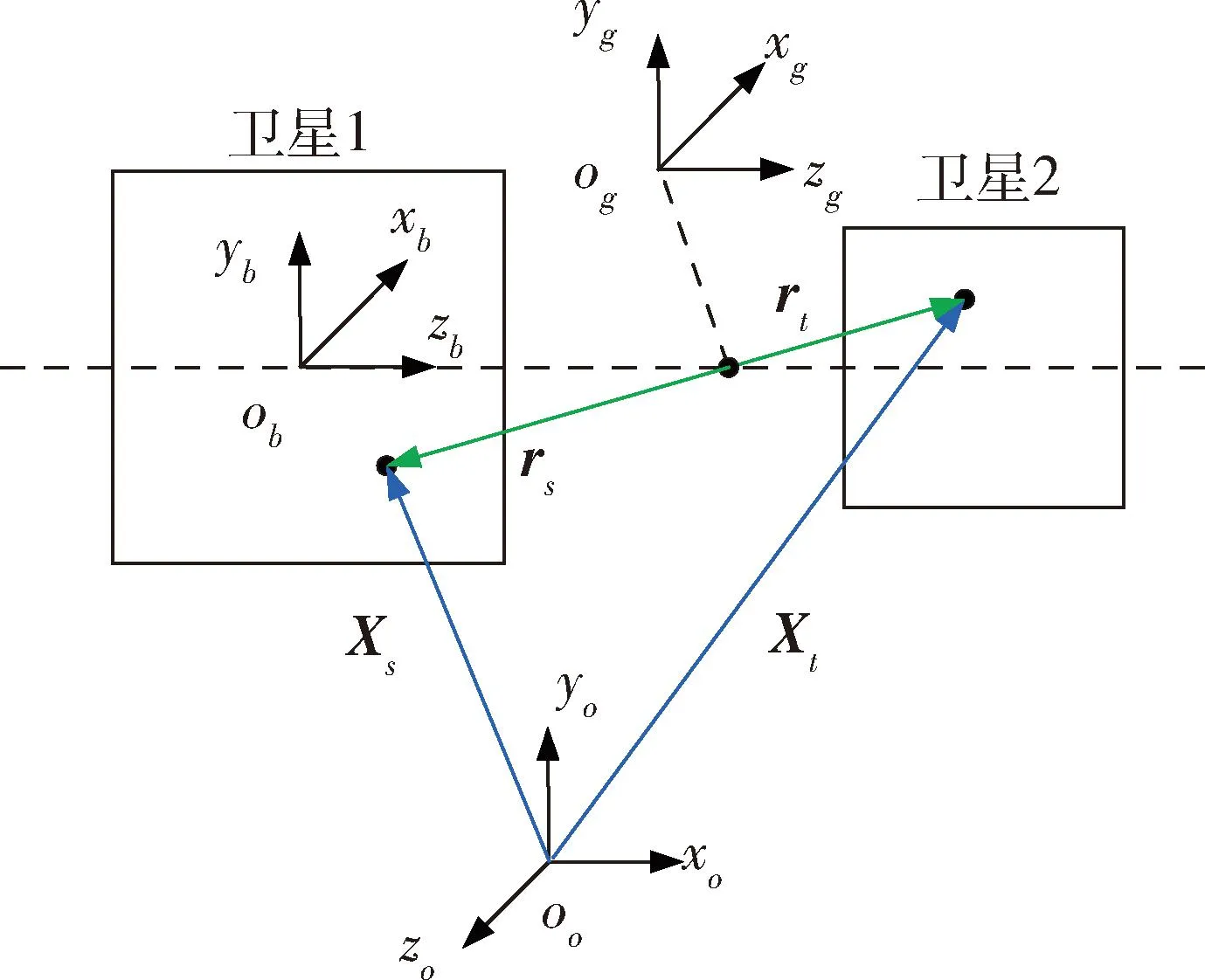
图2 坐标系和矢量定义Fig.2 Coordinate system and vector definition
(1)
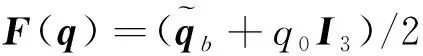
(2)
组装卫星的姿态动力学方程为
(3)
式中,J∈R3×3是组装卫星的转动惯量,Rwi=AwiJwi∈R3×3表示反作用飞轮i相对卫星的转动耦合矩阵,Awi∈R3×3是飞轮i本体系相对b系的姿态变换矩阵,Jwi∈R3×3是飞轮i的转动惯量,θwi∈R是飞轮i相对卫星的转角,Dwi∈R3是飞轮i相对卫星的角速度在飞轮i本体系下的投影矩阵,τb∈R3是飞轮施加给组装卫星的控制力矩.
组装卫星转动惯量J可以表示为
(4)
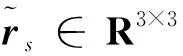
假设3.认为卫星1的质量参数已知,卫星2的质量参数(Mt,rt,Jt)未知.
假设4.认为组装卫星质心位置、速度测量环节均已实现高精度测量.
2 陀螺/GPS/星敏多传感器联邦滤波算法
针对陀螺/GPS/星敏多传感器,设计联邦滤波算法得到全局最优估计,并提高估计结果在故障发生时的可靠性.
2.1 传感器测量模型
陀螺的测量模型为
ωm=ω+b+η
(5)
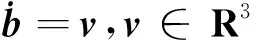
Δω=-Δb-η
(6)
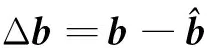
(7)
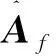
(8)
(9)
(10)
(11)
GPS的测量模型为
qfm=qf⊗qϑ
(12)

(13)
在省略二阶小量后,式(13)的矢量部分近似为
qfwb=Δqfb+ϑ
(14)
星敏感器的测量模型为
lim=li+ei
(15)
其中,li∈R3是星敏感器第i个光轴在惯性系下投影,lim是li的测量结果,ei是星敏感器的测量误差.忽略星敏感器自身的安装偏差,根据姿态变换关系,有
li=AoAflbi
(16)
式中,Ao∈R3×3是轨道坐标系相对惯性系的姿态变换矩阵,lbi∈R3是星敏感器第i个光轴在组装卫星本体系下投影.在省略二阶小量后,式(16)可以近似为
(17)
2.2 联邦滤波算法
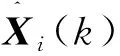

图3 联邦滤波器的一般结构Fig.3 General structure of the federal filtering
(18)
(19)
其中,βi表示信息分配因子,满足信息守恒原理
β1+β2+…+βN+βm=1
(20)
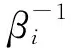
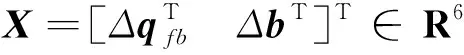
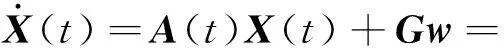
(21)
其中,03×3表示三维零矩阵,记过程噪声w的方差为Qg.离散式(21)可得
X(k)=Φ(k-1)X(k-1)+Γ(k-1)w(k-1)
(22)
记离散周期为Tc,则式(22)中的Φ(k-1)和Γ(k-1)可表示为
(23)
根据式(14)构建GPS量测方程
Z1(k)=H1(k)X(k)+ϑ(k)
(24)
其中,Z1(k)=qfwb(k),H1(k)=[I303×3]成立,记GPS量测噪声ϑ的方差为R1.进一步,根据式(15)构建星敏量测方程
Z2(k)=H2(k)X(k)+e(k)
(25)
其中,
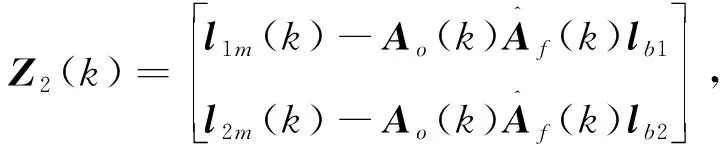
(26)
记星敏量测噪声e的方差为R2.综合上述方程,制定陀螺/GPS/星敏多传感器联邦滤波算法实现步骤如下:
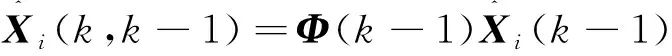
(27)
4)根据式(24)和式(25)进行量测更新(i=1,2)

(28)
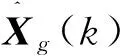

(29)

2.3 残差卡方检验
假设GPS发生了故障,测量模型(24)变为
Z1(k)=H1(k)X(k)+ϑ(k)+fk,φγ
(30)
其中,γ表示故障的大小,fk,φ是分段函数,满足
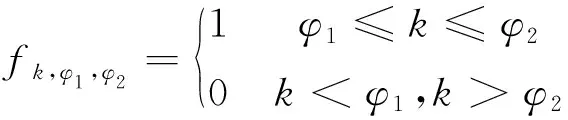
(31)
定义预测残差序列
(32)
协方差矩阵为
(33)
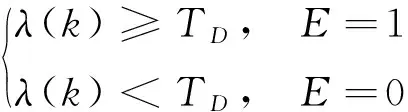
(34)
其中E是故障标识变量,取1表示系统检测到故障,取0表示系统正常.根据奈曼-皮尔逊准则可知,TD取值对应某一误警率Pf,通过查询χ2分布表得到预期误警率对应的门限值,从而依据式(34)进行故障检测.
当E=1时,应立即隔离陀螺/GPS子滤波器估计结果,重构联邦滤波算法,以陀螺/星敏子滤波器输出作为全局估计,并把全局估计反馈给陀螺/GPS子滤波器持续监测故障,直到故障恢复后,再按照2.2节步骤进行,提高算法在故障发生时的可靠性.
3 组装卫星自适应固定时间滑模控制
3.1 组装卫星质量参数辨识
组装卫星线动量在惯性系下投影σ表示为
(35)
其中,ra=-rs+rt成立,A是组装卫星本体系相对惯性系的姿态变换矩阵.记通过喷气施加给组装卫星的外力在惯性系下投影为F,依据动量定理有
σ(k)-σ(k-1)=F(k-1)Δt
(36)
其中,Δt是辨识周期.将k时刻之前的方程累加有
(37)
将式(35)代入式(37)有

(38)
记待辨识量αm=[1/Mtra]∈R4,将式(38)整理为线性最小二乘形式
Bmαm=gm
(39)
此外,组装卫星角动量在本体系下投影H为
(40)
在反作用飞轮作用下,系统满足角动量守恒
A(k)H(k)=A(k-1)H(k-1)=A(0)H(0)
(41)
将式(40)代入式(41)有
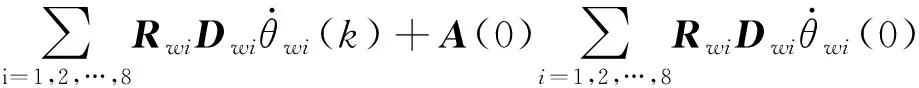
(42)
设待辨识量αJ=[IxIyIzIxyIxzIyz]T∈R6,将式(42)整理为线性最小二乘形式
BJαJ=gJ
(43)
基于式(29)和式(43)建立的回归方程,使用递推最小二乘辨识算法[18]在线辨识未知的质量参数Mt,ra和J.
3.2 自适应固定时间滑模控制
在介绍控制算法前,引入如下定义和引理.考虑如下系统:
(44)
其中,x∈Rn,f代表非线性函数.
定义1[19].如果系统(44)在原点处的平衡状态是Lyapunov稳定的,并且存在T(x0)使系统状态在t≥T(x0)时有x(t,x0)=0成立,那么称系统是有限时间稳定的.
定义2[20].如果系统(44)在原点处的平衡状态是全局有限时间稳定的,并且对于任意的状态初值x0,T(x0)存在上界Tmax>0,使得t≥Tmax时有x(t,x0)=0成立,那么称系统固定时间稳定.

(45)

(46)
同样qe和ωe间满足如式(1)所示的运动学关系,进一步将式(46)转换为

(47)
本节控制目的是通过设计τb,使得qeb和ωe在固定时间Tmax内收敛到零.设计滑模面如下:
(48)
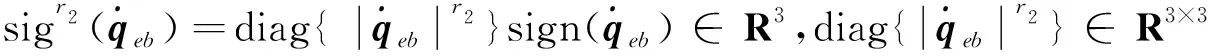

(49)
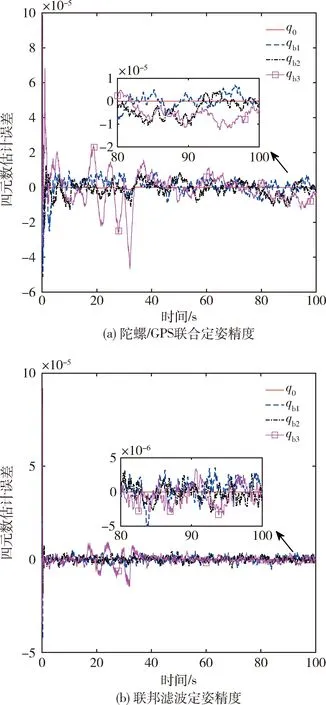
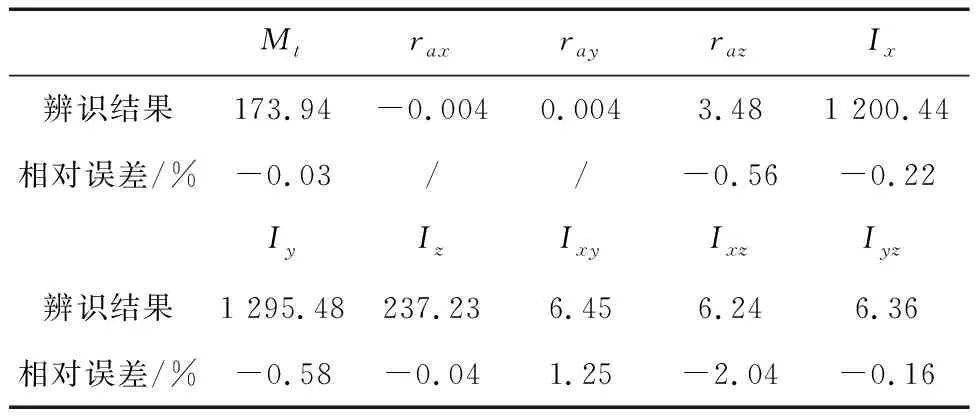
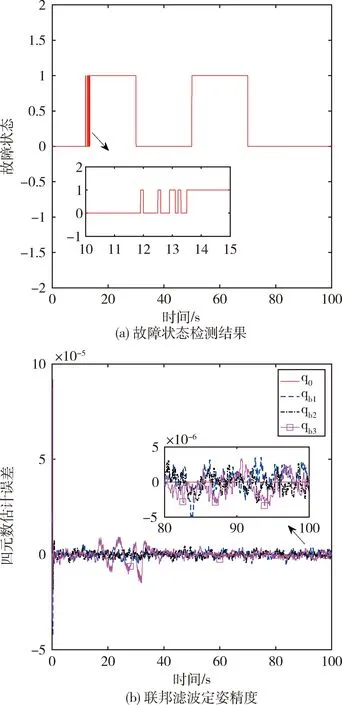
式中,参数满足a>0,b>0,k>1,2>r2>1,1 (50) 证明. 根据滑模面可知,当s=0成立时经过整理有下式成立: (51) (52) (53) (54) (55) 证明. 定义Lyapunov函数V2=0.5sTs,有 (56) αm=3(1-k1)/k1α2(p1k1+1)/(2k1) (57) 式(56)可以缩放为 (58) 将状态空间分为两个区域 (59) (60) 那么根据引理1可知,系统状态将在To1时间内收敛到s=0或进入δ2区域,其中To1满足 (60) 证毕 注2.设计的控制律(52)由组装卫星上8个反作用飞轮提供,每个飞轮驱动指令的获取可参考文献[21]中基于零空间的最优控制分配方法.因不是本文关注重点,这里不展开讨论. 组装卫星质量参数如表1所示,其中质心位置是卫星本体系原点指向各体质心的位置矢量在卫星本体系下投影,转动惯量在卫星本体系下描述. 表1 组装卫星质量参数Tab.1 Assembled satellite inertia parameters 基于表1可计算待辨识参数真值为 考虑陀螺/GPS/星敏测量参数如表2所示. 表2 测量参数Tab.2 Measurement parameters 认为各传感器无故障问题,联邦滤波稳定后将状态估计结果传递给辨识算法,10~15 s施加质心辨识激励F=[sin(πt) cos(πt) sin(t)]TN,15 s~30 s施加惯量辨识激励τb=2[sin(πt) cos(πt) sin(t)]TN·m,30 s后利用固定时间滑模控制完成组装卫星姿态稳定,设置仿真时长100 s. 子滤波器1(陀螺/GPS联合定姿)和联邦滤波的四元数估计精度对比如图4所示.根据仿真结果可知,陀螺/GPS联合定姿四元数估计误差的最大标准差为5.281 1×10-6(1σ),而联邦滤波四元数估计误差的最大标准差为1.427 2×10-6(1σ),因此设计的联邦滤波算法充分利用了组装卫星姿态敏感器冗余配置的特点,相比于卫星1配置的陀螺/GPS联合定姿方法而言,姿态确定精度提高了73%. 图4 四元数估计精度对比Fig.4 Comparison of the quaternion estimation accuracy 参数辨识结果总结于表3,表中数据单位均为国际单位.根据仿真结果可知,基于联邦滤波状态估计结果,设计的参数辨识算法在20s内实现了较高精度的参数估计,最大误差为2.04%. 表3 参数辨识结果Tab.3 Parameter identification results 在此基础上将自适应固定时间滑模控制和PD控制[22]进行对比,PD控制设置调节时间10s,系统阻尼比为1.两者仿真结果分别如图5和图6所示,自适应固定时间滑模控制在15 s内收敛到平衡状态,姿态精度在0.000 2°以内,相比于PD控制而言,具有更快的收敛速度和更高的控制精度. 图5 PD控制精度Fig.5 PD control accuracy 图6 自适应固定时间滑模控制精度Fig.6 Adaptive fixed time sliding mode control accuracy 此外,自适应固定时间滑模控制力矩曲线如图7所示,由于通过参数辨识算法估计了未知的质量参数,提高了控制器的自适应性并降低了参数选取范围,从而改善了控制力矩颤振问题. 图7 控制力矩Fig.7 Control torque 进一步,考虑GPS元件存在故障:在10~30 s内有γ=2(t-10)×10-5的缓变故障,在50~70 s内有γ=0.001的突变故障.故障标识变量E的仿真结果如图8(a)所示,表明设计的残差卡方检验算法检测到了GPS元件的缓变故障和突变故障,虽然E在10~14 s间有滞后和波动现象,但由于缓变故障在发生初期较小,所以漏检问题对于全局估计的影响较小,可以忽略.联邦滤波全局估计结果如图8(b)所示,仿真结果表明经过故障检测、隔离和重构后,故障情形下的姿态确定精度和图4(b)相仿,保证了姿态估计结果的可靠性.此时参数辨识精度和固定时间滑模控制精度和前文相仿,不再赘述. 图8 故障发生时联邦滤波仿真结果Fig.8 Federal filtering simulation results when a fault occurs 上述仿真结果表明,本文建立的陀螺/GPS/星敏多传感器联邦滤波算法提高了姿态确定精度,并具备容错能力;提出的自适应固定时间滑模控制有效抑制了质量参数不确定性干扰,提高组装卫星控制精度的同时改善系统颤振问题. 结合在轨组装卫星姿态敏感器冗余配置和质量参数未知的特点,本文建立了陀螺/GPS/星敏多传感器联邦滤波算法,利用残差卡方检验实现敏感器故障的检测、隔离和重构,结果表明姿态确定精度提高了73%,滤除了99%以上的陀螺漂移,并具备故障容错能力.在此基础上,组装卫星质量参数辨识最大误差为2.04%,自适应固定时间滑模控制姿态精度在0.000 2°以内,姿态稳定度在0.000 3(°)/s以内,有效抑制了测量误差和参数不确定性干扰对姿态的影响,降低了控制参数选取范围改善系统颤振问题,实现了组装卫星的高精高稳姿态控制. 未来与展望:在控制器设计过程中没有考虑执行机构输出受限问题,导致反作用飞轮无法完全复现期望的控制指令,影响系统稳定的动态过程甚至可能导致系统发散.下一步的工作目标是设计考虑执行机构输出受限的自适应固定时间滑模控制.
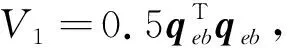
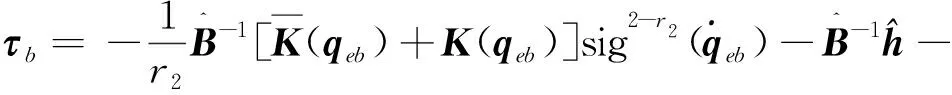
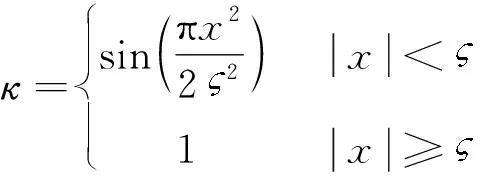
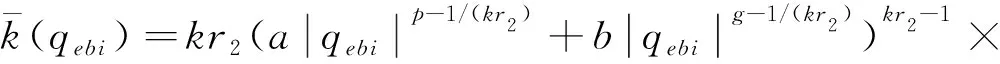

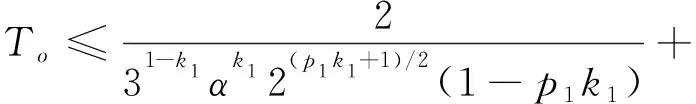

βm=3(1-k1)/k1β2(g1k1+1)/(2k1)
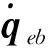
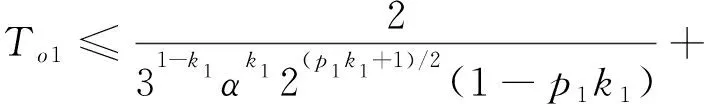
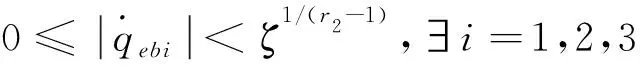

4 结果与讨论
4.1 参数设置


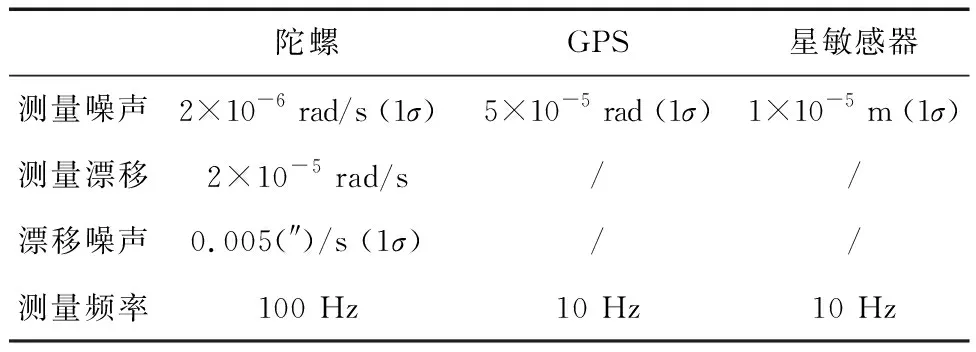
4.2 仿真结果



5 结 论

