基于多重网格的多物理耦合程序开发与验证

李 壮，孙国民，杨子辉，傅 娟，郁 杰

（1.中国科学院合肥物质科学研究院核能安全技术研究所，合肥 230031；2.中国科学技术大学研究生院科学岛分院，合肥 230026）

多物理耦合需要建立合适的网格映射，以实现数据传输。陈军等［1］根据反馈效应的强弱，分别在燃料和慢化剂区域使用一对一映射，在包壳区域采用体积权重的网格映射方式，在Linux系统中完成MCNP5（Monte Carlo N-Particle Transport Code System）和STAR-CCM+（STARComputational Continuum Mechanics+）耦合程序的开发工作。Zhang 等［2］基于OpenMC 和FLUENT 探索自适应平衡算法增强并行性能，对蒙特卡罗模型和CFD（Computational Fluid Dynamics）模型使用相同的单元划分形式，这种一对一映射处理可以简化数据映射，但对于处理规模较大的模型，建模和网格划分需要大量的前处理工作。Xu 等［3］基于数值反应堆物理计算程序NECP-X 和CTF（Coolant-Boiling in Rod Arrays-Two Fluids，COBRA-TF）所开发的耦合程序，在轴向上采用相同划分方式，CTF网格处的值（冷却剂温度和密度）直接被传递到相应的NECP-X 网格上，在径向上传递温度和密度信息时，将CTF 模型每一层的4 个网格的信息平均后传递给NECP-X 模型相同分层。Weng 等［4］在堆用蒙特卡罗分析程序（Reactor Monte Carlo code，RMC）的结构化网格和有限元分析求解软件COMSOL 的非结构化网格之间采取结构化网格实现两个程序之间的通信。Weng 在蒙特卡罗粒子输运计算中采用结构化网格计数，燃料边界处的网格会出现计数偏小的问题。本研究解决了传统数据映射方法前处理烦琐，结构化计数网格存在计数偏小的问题，提出了基于多重网格的数据映射方法，并基于蒙特卡罗粒子输运程序OpenMC［5］和CFD 程序OpenFOAM［6］，采用C++编程语言开发外耦合程序MCOF，通过MCOF 程序在耦合过程自动完成数据交互，实现了灵活高效的数据映射。

1 耦合方法

1.1 耦合工具介绍

OpenMC［5］是一款基于蒙特卡罗方法的粒子输运计算程序。该程序由美国麻省理工学院研发，2012 年末首次对外公布，它支持反应堆及其系统的高保真建模和中子光子耦合模拟计算，经历多个版本迭代，目前其计算精度已被广泛认可。

OpenFOAM［6］是一个完全由C++编程的开源的CFD 求解类库，其面向对象的程序设计支持用户根据实际问题对源码进行修改、扩充。研究中对chtMultiRegionSimpleFoam 进行定制化开发，在能量方程中，新增体积功率源项，使该求解器能够加载OpenMC 计算得到的体积功率。

1.2 OpenMC 和OpenFOAM 的耦合流程

OpenMC 和OpenFOAM 耦合流程如图1所示，数据交互由耦合程序MCOF 完成。耦合程序MCOF 的工作流程主要有如下步骤：

（1）初始化中子物理模型的温度分布和密度分布，调用OpenMC 程序进行粒子输运计算。

（2）从OpenMC 的输出文件提取计数结果，有fission、nu-fission 和kappa-fission，并运用式（1）将计数结果归一化为体积功率。

其中，Pcelli是网格i的功率密度，单位是W·m-3；ncelli是在网格i中每次裂变产生的中子数，为nu-fission 和fission 的比值，单位是neutrons/fission；P是反应堆或组件的热功率，单位是W；kappacelli是网格i的kappa-fission 计数，单位是eV/source；Qcelli是网格i吸收或者释放的能量，为kappa-fission 和fission 的比值，单位是eV/fission；Vcelli是网格i的体积，单位是m3；Keff是有效增殖因子［7］；0.974 表示在压水动力堆的燃料部分沉积97.4%的能量［8］。

（3）将归一化的非均匀分布功率信息加载到OpenFOAM 求解器的能量方程中进行源项更新，并进行热工水力计算，获取温度分布和密度分布。

（4）根据材料卡ID 更新中子物理模型，重复迭代计算，直至温度分布和功率分布收敛或达到最大迭代次数。

1.3 基于多重网格的数据映射方法

为了解决传统数据映射方法前处理烦琐，结构化计数网格存在计数偏小的问题，本研究提出基于多重网格的数据映射方法进行功率信息和密度、温度信息映射。其中，功率信息映射通过构建中间独立的均匀结构化网格实现；温度和密度信息映射的网格划分与蒙特卡罗模型的单元划分一致，并通过此网格完成温度和密度信息映射。

1.3.1 功率信息映射

功率信息映射如图2 所示，首先，将计数网格中的计数归一化为体积功率，归一化公式如式（1）所示；然后构建中间均匀结构化网格（以下简称中间网格）映射体积功率；最后，通过mapFields 程序［6］将中间网格上的功率信息加载到热工水力模型指定区域，如图2 中热工水力模型的燃料区域。

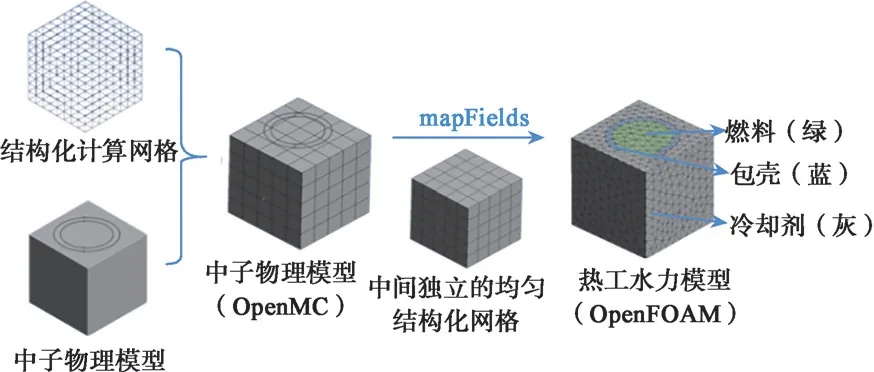
图2 中间独立结构化网格功率信息映射图示Fig.2 Independent structured grid for mapping power information

结构化计数网格在燃料边界处包含较少的可裂变材料，会出现计数偏小的问题，导致归一化的功率出现巨大偏差。如图3 所示，以20×20 的网格未修正结果所示，（a）为OpenMC 计算的裂变率结果，可见在燃料的边界处的计数偏小；（b）为中间网格的体积功率映射结果，可见边界处的归一化功率值偏低；导致（c）和（d）中燃料部分边界处的功率值偏低。计数网格细化可以最大限度逼近燃料边界，提升计数精度，但在蒙特卡罗粒子输运计算的粒子总数一定的情况下，更加精细的网格会导致更高的计数不确定性，因为每个计数网格中的结果由少量源粒子确定，使得计数不确定性增加；而要保证精细的网格具有相同的计数精度，就要增加蒙特卡罗计算的粒子数和计算时间成本［9］。图4 是100×100 的网格裂变率的计数结果，计算中设置200 个批次（batch），每批次108个粒子，100 核并行计算耗时129 分钟。由图4 可见，在边界附近还是会出现锯齿状，数据映射出现燃料边界局部功率偏低的现象。

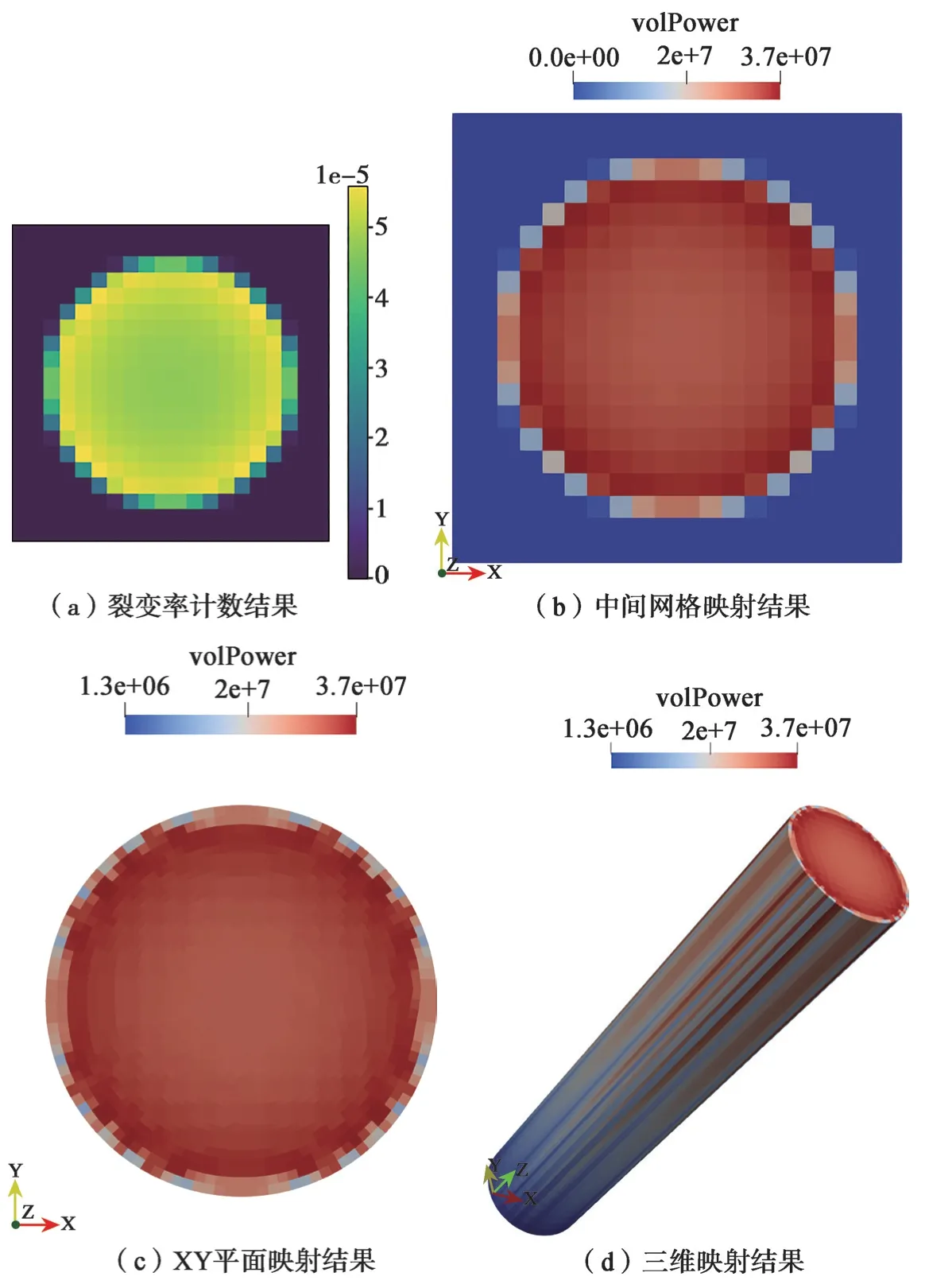
图3 20×20 网格未修正结果Fig.3 20×20 Grid uncorrected results

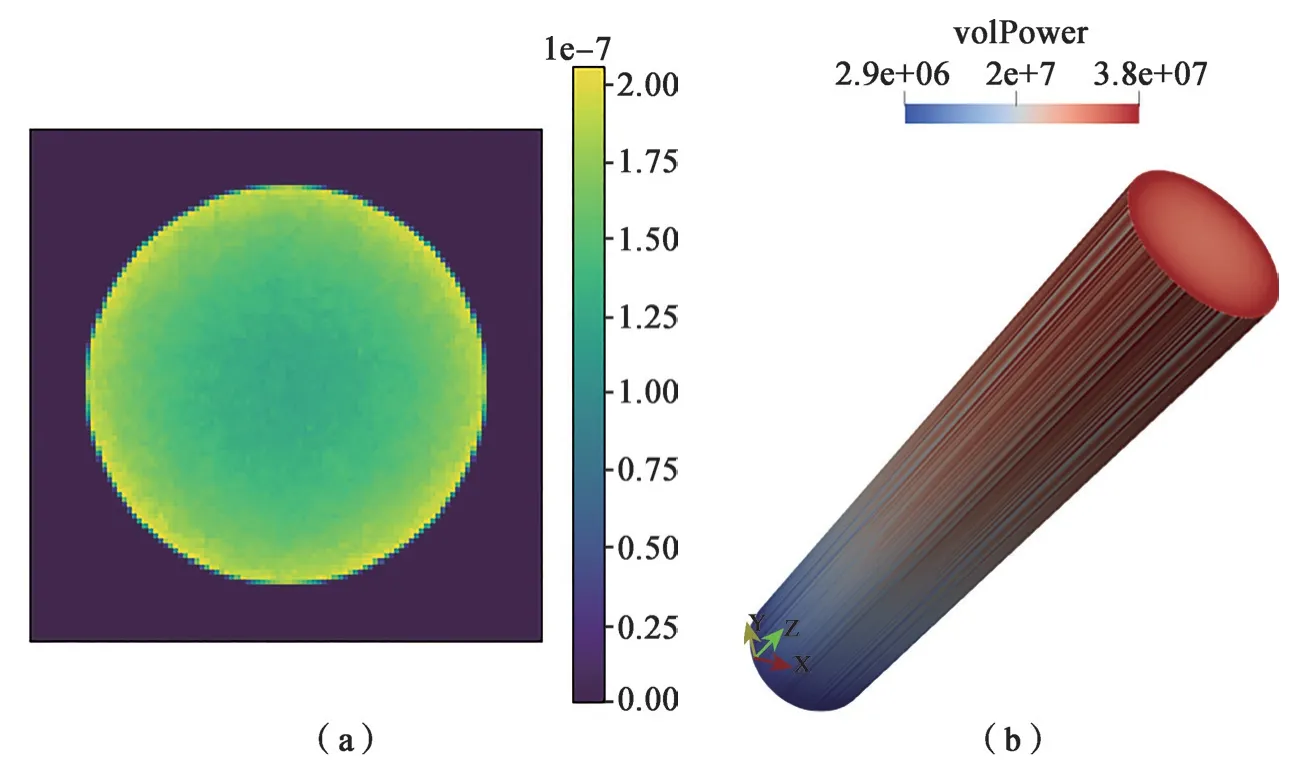
图4 100×100 网格裂变率的计数结果（a）和映射结果（b）Fig.4 100×100 grid fission rate（a）and mapping result（b）

文章基于改进萨瑟兰-霍奇曼多边形裁剪算法（Sutherland-Hodgman algorithm）［10，11］，在燃料的曲线边界处通过分割处理、逐边裁剪，自动辨识裁剪窗口，裁剪出目标区域并计算出可裂变材料的体积修正因子，再进行功率归一化，改善数据映射的结果。与此同时，本文还展开对计数网格无关性验证的研究，见表1。

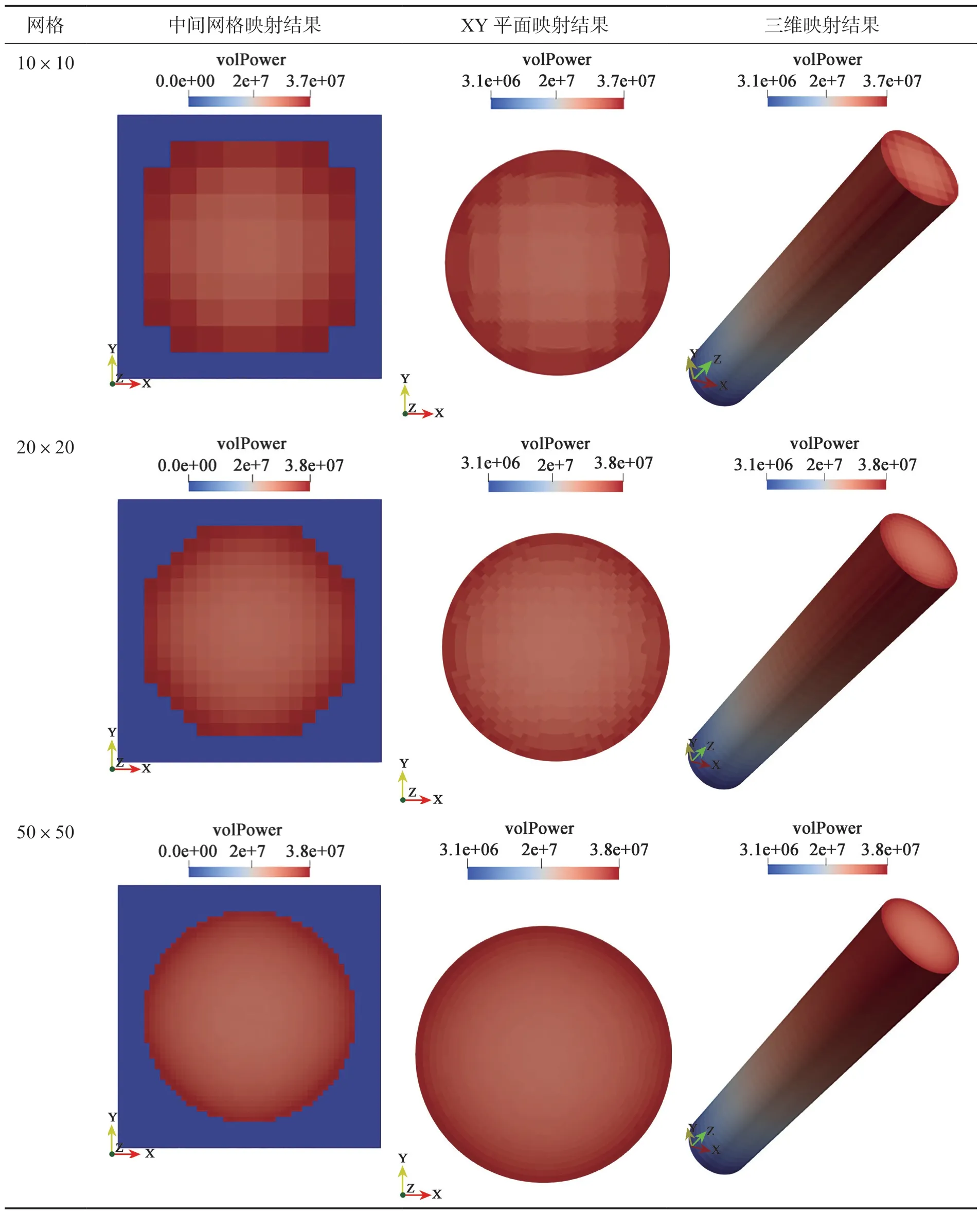
表1 计数网格无关性验证Table 1 Material thermal property parameters

由表1 的结果可见，经过修正，在燃料边界处不再出现功率值偏低的地方；经过三种网格的计数统计，10×10 网格、20×20 网格和50×50 网格的归一化功率最高值分别为3.7×107W·m-3、3.8×107W·m-3、3.8×107W·m-3。由于10×10 网格的计数精度相对偏低，50×50网格的蒙特卡罗粒子输运计算耗时较长，本文采用20×20 网格验证进行映射方法和耦合程序验证。

1.3.2 温度和密度信息映射

在温度和密度信息映射方面，首先在中子物理模型中显式地划分出若干单元，然后热工水力模型依据中子物理模型的单元划分，在热工水力模型中隐式地划分出网格单元（以下简称伪单元），最后将伪单元的温度和密度均值传递到中子物理模型对应单元，更新对应材料卡的温度和密度。值得注意的是，该信息映射分为径向映射和轴向映射，在径向映射时，根据哈尔滨工程大学的Zhang 等［12］的研究，燃料沿径向的温度分布对功率分布的影响极小。因此，本文在处理中子物理模型时，燃料径向上没有划分单元，同时考虑减小温度映射的误差，冷却剂在径向上进行单元划分，如图5 所示。轴向映射时，通过在轴向上划分出多层来进行映射。层数越多，划分越精细，蒙特卡罗粒子输运计算消耗计算资源就越大［13］。

图5 蒙特卡罗模型径向单元划分Fig.5 MC model radial cell division

1.3.3 耦合程序收敛判断

对于耦合程序计算收敛的判断问题，伊利诺伊大学的研究者［14］和加州大学的研究者［9］认为可以通过判断有效增殖因子和温度是否收敛终止程序。有效增殖因子判断收敛只能判断出蒙特卡罗粒子输运计算达到收敛，使得有效增殖因子和温度判断收敛不能反映出中子物理和热工水力的反馈效应，而温度和功率判断收敛能够反映出中子物理模型的功率空间分布对热工水力模型的温度空间分布的影响。因此本文选择温度和功率作为耦合程序收敛的判据，判断收敛的计算式如式（2）和式（3）所示。

其中，N为网格总数；n-1 表示前一次耦合计算；n表示当前耦合计算；celli是网格索引；RMS为每个网格前后两次耦合计算的温度或功率差的平方与网格总数的比值；ΔT和ΔP分别是温度收敛因子和功率收敛因子。耦合迭代10次后，当收敛因子ΔT和ΔP都小于1%时，可视为耦合计算达到收敛。

2 程序开发与验证

2.1 程序开发

MCOF 耦合程序主体采用C++编程语言完成开发。MCOF 耦合程序主要有三个功能模块，分别为功率映射模块、材料更新模块和耦合模块。功率映射模块控制蒙特卡罗程序与CFD程序的功率传递，材料更新模块控制CFD 程序和蒙特卡罗程序温度密度传递，耦合模块主要包含耦合求解中程序的调用策略和收敛方案。

2.2 程序验证结果与分析

本研究基于多重网格映射方法完成耦合程序开发，参考单棒模型［15］进行验证。单棒如图6 所示，绿色部分是包壳，蓝色部分是冷却剂，红色部分是燃料，模型的几何和物性参数均采用参考文献中的数值［15］。

图6 IPR-R1 TRIGA 单棒模型Fig.6 IPR-R1 TRIGA single rod model

耦合迭代收敛后的功率和温度沿轴向中心线分布，如图7 所示，与参考文献［15］结果的总体相对偏差在3%以下。图8 所示模型高度的二分之一处沿径向的功率分布和温度分布，与文献总体偏差小于1%。其中功率分布通过多重网格映射方法和OpenFOAM 的mapFields 程序插值后，与参考值符合良好。耦合计算结果充分反映了中子物理和热工水力的相互作用，体现了反应堆堆芯的反馈机制。耦合迭代计算过程的功率收敛因子和温度收敛因子如图9 所示，最终收敛因子分别为0.45%和0.28%。

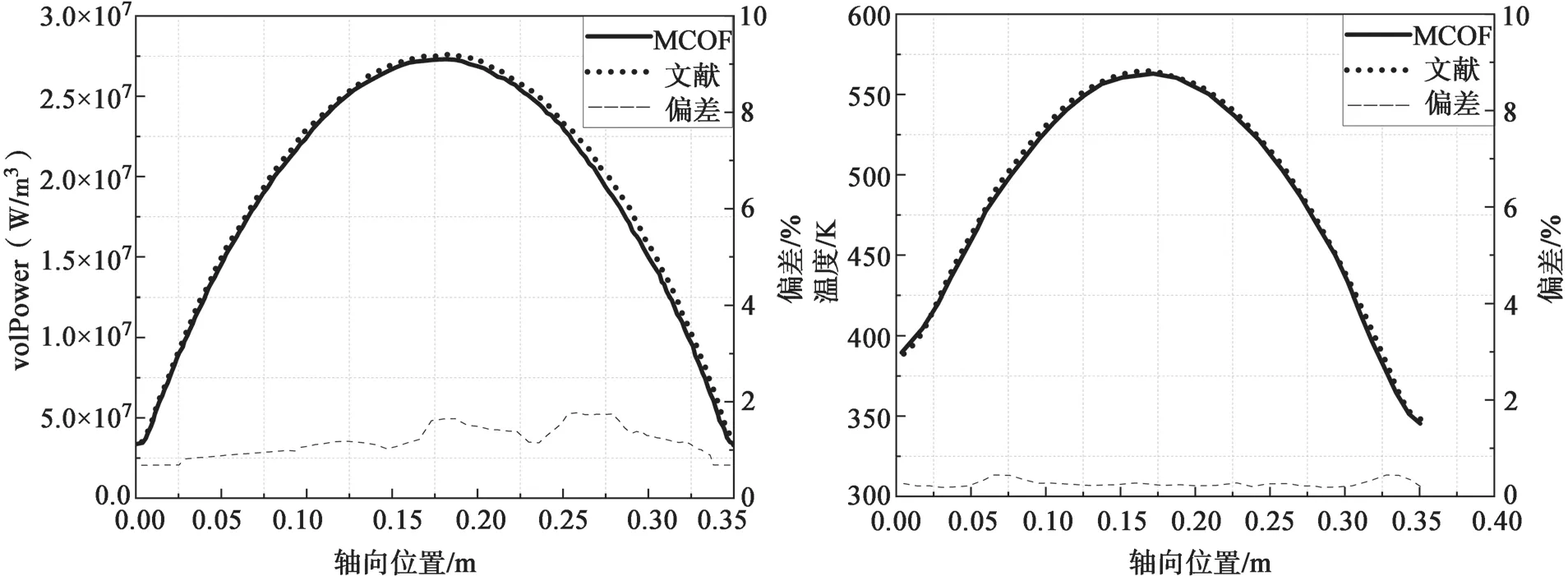
图7 沿轴向功率分布和温度分布Fig.7 Power distribution and temperature distribution in axial direction

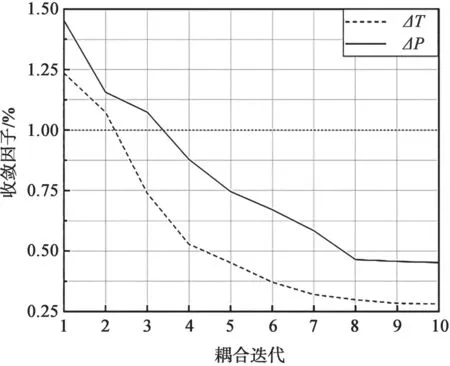
图9 功率收敛因子和温度收敛因子随耦合迭代次数的变化Fig.9 Variation of power convergence factor and temperature convergence factor with the number of coupling iterations

3 结语

针对传统数据映射方法前处理烦琐，结构化计数网格存在计数偏小等问题，采用多重网格数据映射方法开展耦合计算研究。通过单棒模型对数据映射方法和耦合程序进行耦合计算验证，与文献结果进行了对比，功率分布曲线和温度分布曲线符合良好，验证了所提出数据映射方法的正确性。