相似三角形的新定义问题探析
韦柳香













[摘 要]相似三角形的新定义问题相对复杂,学生普遍觉得解决此类问题比较困难。文章结合几则典例,从四个方面分析相似三角形的新定义问题,以培养学生学习新知与运用新知的能力,发展学生的学科核心素养。
[关键词]相似三角形;新定义;初中数学
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2023)26-0026-03
新定義问题多以初中学生已学知识为出发点,通过类比、引申或拓展给出新的数学概念或数学公式等,以阅读材料的形式介绍给学生,让学生在新旧知识之间建立联系,理解其内容、思想与方法,掌握其本质,然后,通过类比、猜想与迁移的方法利用新知识解决问题。近些年,相似三角形的新定义问题在考试中频频出现,学生普遍觉得解决此类问题比较困难,以下笔者结合几则实例做进一步分析探讨。
一、“叠似”三角形
“叠似”三角形是指位于一个角的平分线两边且有一条公共边的两个相似三角形,这是一对特殊位置关系的相似三角形,它们不仅相似,且共边,分居在角平分线的两旁。
点评:“叠似”三角形组成一个四边形,四边形的一条对角线平分一个内角,已知两个三角形中有共点的两边长的长,可以求得其余四边的长,这里共边发挥了桥梁作用,是其他两边的比例中项。
二、“等角等积”三角形
“等角等积”三角形是指面积相等的两个三角形,且它们有重合顶点,重合顶点所在的角相等。当等角等积的两个三角形都是直角三角形时,将其不重合的顶点顺次相连,可以得到一组相似三角形。
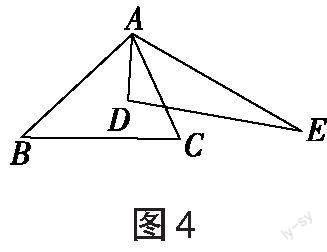
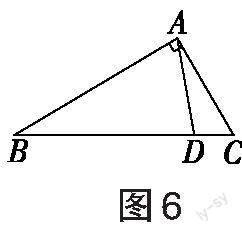
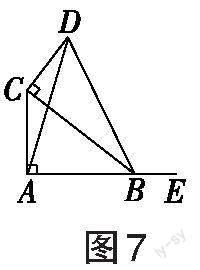
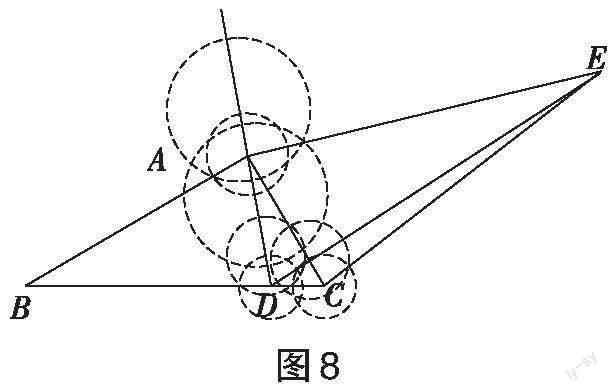
[例2]我们定义:如图4,在[△ABC]和[△ADE]中,若[∠BAC=∠DAE],[S△ABC=S△ADE],则[△ABC]和[△ADE]关于点[A]成“等角等积三角形”。(1)如图5,[∠BAC=∠DAE=90°],[S△ABC=S△ADE],求证:[△ABD ]∽[△AEC];(2)如图6,在[△ABC]中,[∠BAC=90°],[D]为[BC]上的一点,连接[AD]。用直尺和圆规作一个点[E],使[△ABC]和[△ADE]关于点[A]成“等角等积”三角形(保留作图痕迹,写出必要的文字说明);(3)如图7,[AC⊥AE],[AC=4],[B]为射线[AE]上一点,作[△BCD],使[A],[D]位于[BC]的两侧,[∠BCD=90°],[S△BCD=12],连接[AD],则[AD]长的最大值为 。
(2)过点[A]作[AE⊥AD],以AC为一条边作[∠ACE=∠ADB],[CE]与[AE]相交于点[E],如图8所示。
点评:第(1)小题的模型与解题方法对于第(2)小题的作图,以及第(3)小题的求最值很有借鉴意义,因为等角等积的两个直角三角形的图形中,会产生一组相似三角形,所以作等角可以得到相似三角形,从而得到等角等积的三角形。
三、“二倍角”三角形
“二倍角”三角形是指有一个角是另一个角二倍的三角形,当这个三角形是等腰三角形时,这个三角形就是等腰直角三角形或顶角为36°的等腰三角形。通过相似三角形可以证得二倍角所对边的平方等于1倍角所对边的平方与另两边乘积的和。
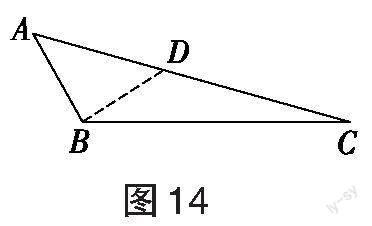
分析:(1)分两种情况,即顶角是底角的二倍时和底角是顶角的二倍,然后利用三角形内角和定理求底角的度数;(2)类比小思同学作辅助线的方法,将二倍角的其中一边反向延长,使延长线段的长等于另一边长,构造相似三角形,利用相似三角形对应边成比例,证明结论;(3)由性质探索 可知:AB2=AC(BC+AC),把AB=6,BC=5代入,建立关于AC的一元二次方程,解一元二次方程求得AC的值;(4)如图14,作∠CBD=∠A,交AC于点D,则△ABD是2倍角三角形。由△CBD∽△CAB求得CD的长,再由“二倍角”三角形的性质,得到AB的长。
解:(1)当等腰三角形的内角分别为[x],[x],[2x]时,[4x=180°],解得[x=45°],当等腰三角形的内角分别为[x],[2x],[2x]时,[5x=180°],解得[x=36°],[2x=72°],∴底角的度数为45°或72°,故答案为45°或72°。
(3)由性质探索 可知:[AB2=AC(BC+AC)],∴[AC2+5AC-36=0],解得[AC=4]或-9(舍去),故答案为4。
点评:本题重点探究了“二倍角”三角形的性质,即二倍角所对边的平方=一倍角所对边的平方与另两边乘积的和。这条性质是通过构造母子型相似三角形获得的,在母子型相似三角形中,共用边是在同一直线上的两边的比例中项。然后应用二倍角的性质求三角形的边长,利用二倍角的性质求三倍角三角形的边长,体现了探究二倍角三角形的价值。
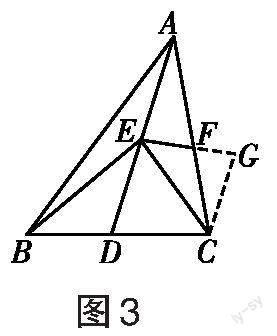
四、“布洛卡点”型三角形
三角形的布洛卡点是法国数学家和数学教育家克洛尔于1816年首次发现的,但他的发现并未被当时的人们所注意。1875年布洛卡点被一个数学爱好者布洛卡重新发现,并用他的名字命名。若△ABC内一点P满足∠PAC=∠PBA=∠PCB=∠α,则点P是△ABC的布洛卡点,∠α是布洛卡角。
[例4]若△ABC内一点P满足∠PAC=∠PBA=
点评:布洛卡点是三角形中一个特殊的点,它与三个顶点连接后,形成了一组等角。本题既考查了学生对于布洛卡点的理解,也考查了学生对于等腰直角三角形及等腰三角形性质的理解与掌握。

