将“思考题”结构化打包，还给学生

一、“你遇到过类似的吗？”

思考题比较复杂，对学生而言具有一定的挑战性，具备发展思维的独特价值。大部分学生在遇到思考题时会不假思索地“知难而退”，思维的深度无法挖掘。作为教师，我们要让学生找到思维的生长点，从相互关联的思考题中找到学生思维发展的线索，实现思维“爬坡”。

例如在解决图1所示的问题时，我们可以帮助学生联想有没有碰到过类似的题目，于是学生很容易联想到图2所示的题目，同样是已知正方形面积求圆的面积，并且正方形的边长用学生现有的知识是无法求出来的。用这样的方法导入思考题的讲解可以帮助学生建立知识体系，获得结构性认知。

二、“你觉得用什么知识解决？”

在找到相似题型后，教师可以顺势提问：“你觉得用什么方法可以解决这个问题呢？”此时教师不能限制学生的思维，让学生“放肆想”“大胆说”。

在计算圆的面积时，学生遇到的基本都是已知半径、直径或周长求圆的面积。这样形成思维定式后，已知半径的平方求出圆的面积便是一个难点。圆环面积计算是比较复杂的，但是由图2学生会联想到借助正方形计算圆的面积的经验，帮助他们思考计算圆环面积的方法。学生会产生这样的思考：解决问题的关键在于算出“两个圆半径的平方差”是多少，而半径的平方差又与正方形的面积差有关。图中阴影部分面积的一半恰好是正方形的面积差，也就是大圆半径的平方减去小圆半径的平方。由此可见，根据半径的平方计算圆的面积的思考方法对计算圆环的面积起到了经验支撑作用。

三、“你能改编题目考考大家吗？”

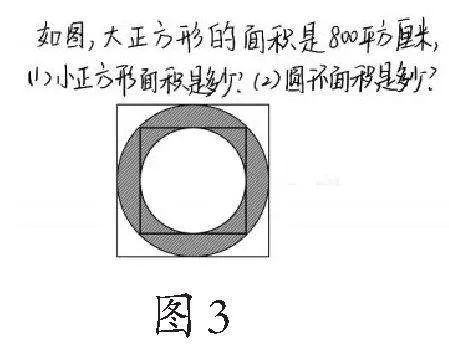
对思考题中所蕴含数学思想方法的领悟，光靠老师引领解题是不够的，需要学生自己领悟，而学生领悟的一个好的途径就是自己对题目进行改编。在改编的过程中，学生会将所学方法进行结构性整合，由方法引申出变式题，使复杂的方法简化，使学生思维活化。例如图3所示就是我班学生根据前面的思考题编制的变式题。

教师要允许学生编写的题目暂时不够完善，肯定学生的探索过程和思考价值，并帮助其将题目进一步完善。收集有价值的题目，为学生搭建一个平台，让他们互相解答对方的题目，交流对知识的理解，让思维传递起来。