数与运算中的累加与细分

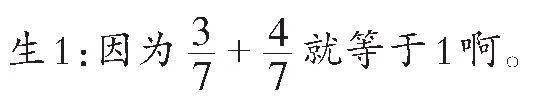
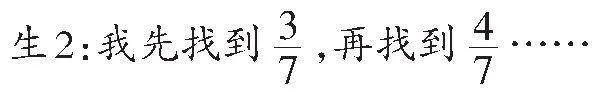
在本文中，累加与细分是指相同计数单位的叠加或细分。比如，计算0.5＋0.3时，从0.5开始，以0.1为单位，连续累加3次，就得到0.8，运算过程就是计数单位累加的过程。在除法运算中，遇到较大的计数单位除不尽时，把余下的进行细分，转化为较小的计数单位，使得计数单位的个数变多，再继续平均分。如果上述的累加与细分在小学数学中用得恰当，会让学生感受到数的一致性，即获得“大概念”。

笔者以累加与细分方法梳理课为例，沟通累加与细分之间的联系。

一、初建结构：从“数”到“数”，探寻数数的神秘性

初建结构看似无心，实则有意。意在从人人可想、人人会想的知识出发，引发联想，勾连出相关知识链条，初成体系。

【课堂链接】

师：图1中有多少个泡泡？你是如何知道的？

生1：我数1个珠子便写上1个数，数到最后1个数是几就有多少个。

生2：我是3个3个地圈，一共圈了5个圈，三五十五，所以有15个。

生3：我把这些泡泡分成两边，然后数出左边有7个，右边有8个，一共是15个。

师：在数的过程中哪个数最重要？

生：在数的过程中，最重要的数是1，有了1就可得到2、3、4……

生：对，可以得到无数个数。

师：这个“1”就是整数最基本的计数单位。所有的数都是通过数得到的，即把计数单位进行累加便可得到无数个数。

接着，教师请学生列举学过的数，并说说它们各自的计数单位。

这样的设计，基于数泡泡的情境，让学生结构化理解“数的意义”。

二、建立结构：在数线上找寻数，体会数与形的一致性

要使结构不散，贵在能放善收。探寻数的根源后，我出示一条没有任何标记的直线，让学生在数线上找寻数。

【课堂链接】

师：别小看这条线，它里面可藏着千军万马呢！想一想，数线里可能隐藏着什么知识？

这是一个开口大、联想空间大的题目。学生七嘴八舌，兴趣盎然。

生：它可以表示一段路程。

生：这条路上的起点站一个人，隔一段距离又站一个人，可以站好多人。

生：它可能有1分米长吧。

设问、疑问、反问，学生展开想象的翅膀，讨论、质疑、达成共识。学生的思维得到深化，发散思维能力得到升华。这时的学生处在“愤”和“悱”的状态，教师趁机抛出问题。

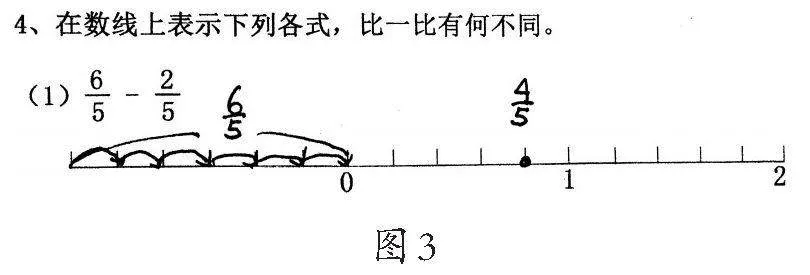
出示学生作品，如图2。

师：这位同学找的是0.6，他找对了吗？

生1：不对，这个不是0.6，要平均分的。

生2：我先找到第一个点（手指指向0后面的第一条小竖线位置），然后继续这样找到第六个点。

师：你找到的第一条小竖线表示什么？（生2：0.1）嗯，你是先找到你认为的0.1，再继续，直到找到6个0.1。怎么确定0后面的第一条竖线表示的就是0.1呢？

生2：我随手画的竖线，不太确定。

生4：因为有了“它们”，才有了更多的“它们”。

生5：它们都是计数单位，把计数单位加起来可以得到很多数。

学生刚开始是碎片化思维，把数和形割裂开思考，这时学生找到数形结合的方向，把散点知识再次结构化，问题得到顺利解决。让学生再次体会：凡数源于数，所有数都是计数单位的累加。数的来源结构化初步浮出表面。

三、应用结构：在数线上找数、找算式，体会数与运算的一致性

通过数数与找数的活动，让学生经历了无意建构与建立结构的过程，积累了一定的结构化活动经验，在此基础上让学生应用此结构在数线上找寻算式。

【课堂链接】

师：（出示下面这道题）请你试一试，并说说你的方法。

生1指着数线上1对应的位置说：就是“1”这里。

师：你怎么知道是这里？

师：题目要求表示计算过程，你的“过程”表示在哪呢？

师：找到结果了吗？

生2摸着头沉思，没回答。

师：你遇到什么困难了吗？

生2：不知怎么合起来。

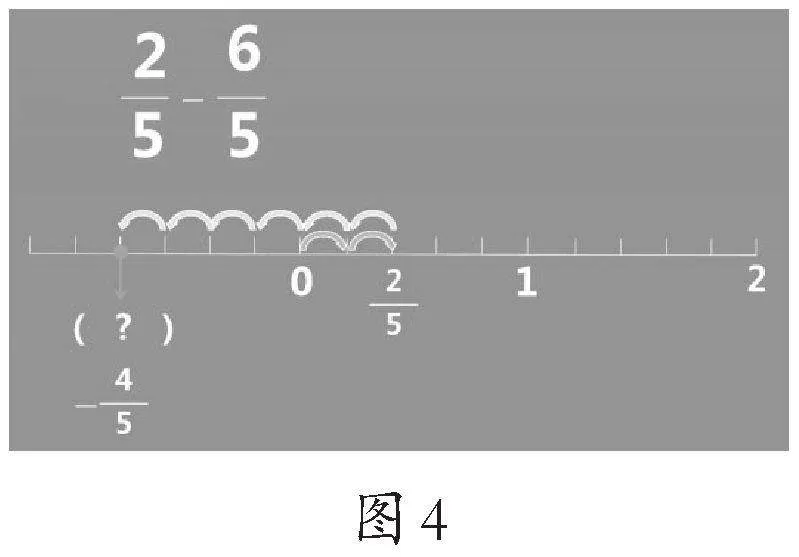
从学生的回答可知，学生只关注静态的结果，直接找到“1”，而不知其所以然，无法把算式计算的动态过程在线上表示出来。通过争辩、思考、引导，学生豁然开朗，明白结果与过程的区别，明白不但一个数可以数出来，计算过程中也在数，结果也是数出来的。这样，不仅让学生明白原来数和数的加法是一家，而且进一步加深了学生对加法算式与数的同源结构的理解。接着，教师出示减法算式，让学生研究与探讨，然后各小组汇报研究结果。

生4：我觉得减法也可以像加法一样。

生：老师，这道题不够减，我们还没学过。

生：我会，不够减时结果是个负数。

师：虽没学过，相信你们能突破。试试吧！

学生进行研究与探讨，而后汇报。

学生从加减法在数线上的方法结构的一致性悟到“减法其实是倒着数，即逆向累加”。不是刻板地模仿，而是在变化中感悟结构的变与不变。

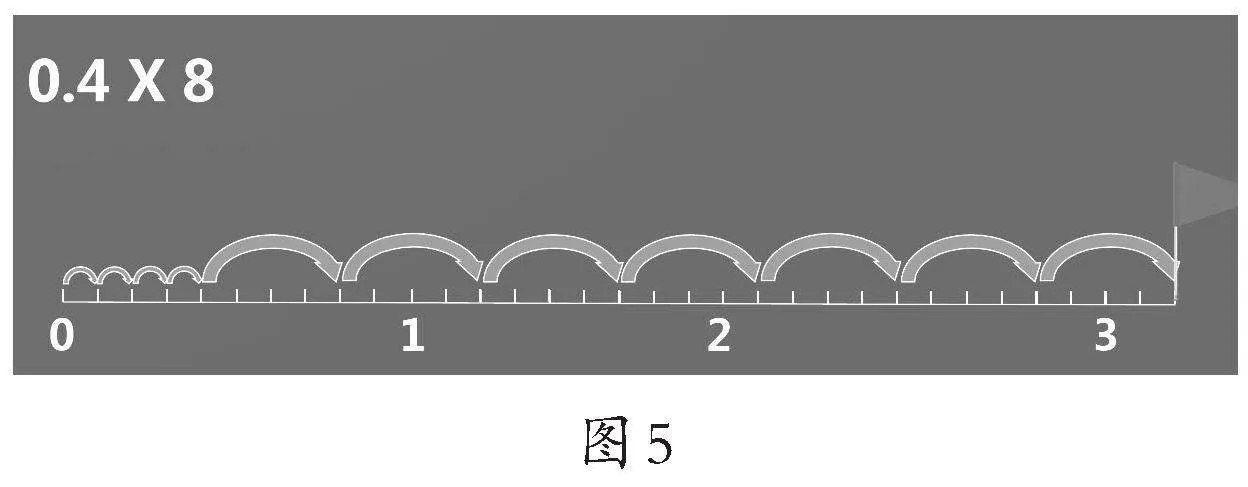
有了前面在数线上找“数与加减算式”的过程与方法建构，学生感受到结构的力量，主动提出要探讨数线上乘法和除法的奥秘，如0.4×8，学生总结出“先以0.1为一小步开始向右数出4小步，到达0.4，而后以0.4为一大步再向右走7大步，一共走8大步来到3.2这个点，即是目标”。（如图5）

从初建结构到建立结构再到应用结构，是结构化教学的一个飞跃，旨在让学生尝试把数和运算与数线联系起来，把过程和结果关联起来，不再分割，让多元表征形成一个整体，在应用结构中，思考用结构化思维解决问题，培养推理意识，提升运算能力。

四、延展结构：在数线上寻找更多运算，体会数与运算的结构性

学生充分体会到加、减、乘结构的一致性，都可以数出来，都是计数单位的累加，那么除法又是怎么样的？学生带着好奇心，走进除法世界。

【课堂链接】

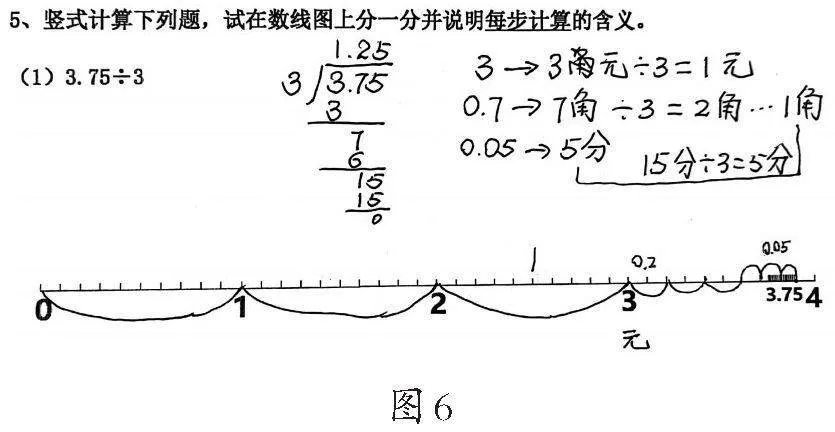
师：请用你掌握的知识和经验，在数线上表示出3.75÷3的过程和结果，并说说与加、减、乘的区别与联系。

生：此问题好像和前面的方法不一样。

虽然学生能很快在算式上计算出结果是1.25，但把每一步在数线上表示出来时却遇到困难，这也正好说明运用SOLO分层理论分析时所发现的：学生的思维层处在多点结构，未能把多种表征进行关联和对应。

师：请同学们根据算式编一个故事吧。

生：假如现在有3元7角5分钱，要平均分给3个人，先把3元平均分成3份，每人1元，刚好把3元分完。

生：第二步分的是7角，仍平均分成3份，每人2角，还剩下1角。第三步分5分钱加上1角，一共15分，平均分成3份，每人刚好是5分钱。

生：最后加起来就是1元2角5分。

师：这里的3元、1元、7角等，在这个算式中能找到它们的原型吗？

生：2角就是小数点后的那个2，是0.2；5就是商的小数点后面的第二位，它是0.05。

生：（如图6）第三步分的是第二步剩下来的1个0.1（10个0.01）加上5个0.01（0.05），共是15个0.01，平均分成3份，每份是5个0.01，刚好分完，最后把1、0.2、0.05这三部分合起来，即1+0.2+0.05=1.25。

除法的计算与表达，对学生来说均是难点，但由于知识的结构、方法的类似，引导学生通过关联，为“断层”搭建脚手架，体会到除法是乘法的逆运算，其中共有结构的关系：以“和”为首，减法与加法互逆，乘法是特殊加法的简便表达，而除法是乘法的逆运算，具有高度的一致性。除法与众不同：加、减、乘是计数单位的累加，而除法是对多个单位的细分，一个累加一个细分，构成了数与四则运算丰富且独特的数线世界。

五、巩固结构：从数与运算想开去，体会“累加与细分”的延展性

结构已构建，思维已打开，断层处已接驳，此时学生只需更大胆地从“想”到“展”，在已有结构里寻找类似，并进行迁移、联想。

【课堂链接】

师：难道仅有数和四则运算才有累加与细分吗？

生1：钱也可以累加与细分，比如，1元钱是由100个1分累加得到的。

生2：厘米也可以累加，9厘米就是由9个1厘米累加得来的。

生3：面积也可以累加，还有体积。

生4：角度应该也可以累加，就是1度、2度、3度，变成很大的角。

师：可否举个细分的例子？

生5：反过来就是细分了。

生6：比如9厘米，平均分成9份就又回到了1厘米。

生：对哟！一步步倒回来就是细分了。

生：累加是积小步成多步至千里，积少成多；细分是从大步变小步了，由多变少。

师：还有其他想法或疑问吗？如果在图7的各幅图中，我把各个单位去掉，右边的图形表示“1”，那左边的图形分别表示多少呢？

生1：第一幅图中短线段表示十分之一，因为长线段被平均分成了10份。

……

“无结构不教学”，这节课，紧紧围绕计数单位的“累加与细分”，通过“五构”法梳理、建立数与运算的关键结构，即都是“数”出来的，知识的世界变幻莫测，但结构的教学稳定而深远。知识结构化让零散的知识串联，通过手拉手形成体系和网络。知识的结构化带动方法的结构化，不断找寻知识链接，以内在关联促进认知结构的发展，从而形成结构化思维。