驻足思考 由“会”生“慧”

在日常练习课上，不少老师犹如导游一样，督促学生快点儿做题，一题做完开始做下一题，一页做完开始做下一页。细想一下，我们节省下来的时间有没有让教学高效起来？真正做到“减负提质”了吗？学生有没有达到练习的目的呢？然而事与愿违，学生在我们的催促下逐渐变得不讲过程，只看结果，做完就是目的，很少思考题目为何这样做。

下面笔者以北师大版教材五年级上册第三单元“因数与倍数”中“3的倍数的特征”一课的“练一练”为例，谈谈自己的做法。

教学片段一

1.“练一练”第1题（如图1）。首先引导学生读题后独立完成，并请学生说一说是怎么判断的。学生都能够利用所学知识给出正确的判断和理由，但是此题我并没有到此结束，而是又组织了一场交流活动。

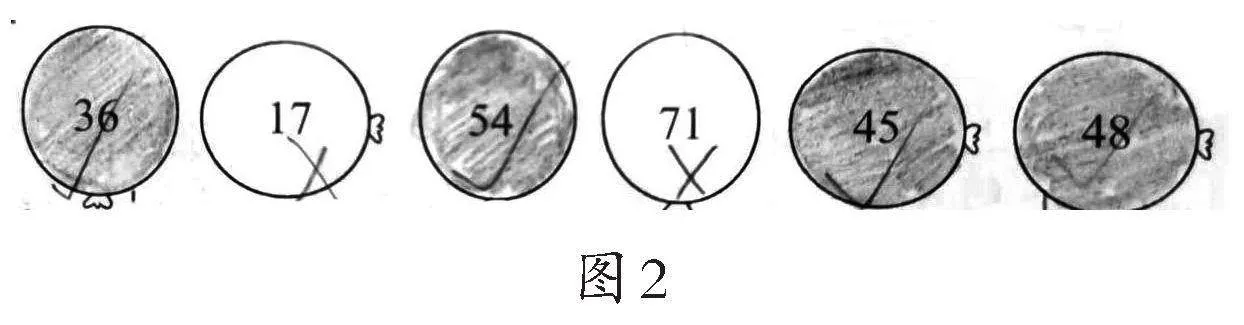
师：（出示学生完成的作业，如图2）你有什么发现？

生：我发现17和71这两个数的个位和十位上的数字交换了一下，它俩都不是3的倍数。

生：我发现17不是3的倍数，交换了它的个位和十位上的数字之后，也不是3的倍数。

生：我发现54是3的倍数，交换了它的个位和十位上的数字之后，还是3的倍数。

师：48是3的倍数，那84呢？能否把这个发现再说一说？

生：如果一个两位数不是3的倍数，交换它的个位和十位上的数字之后，也不是3的倍数；如果一个两位数是3的倍数，交换它的个位和十位上的数字之后，还是3的倍数。

生：我认为不一定非得是两位数，几位数都可以。如果一个数不是3的倍数，随便交换它的数位上的数字之后，组成的新数也不是3的倍数；如果一个数是3的倍数，交换它的数位上的数字之后，组成的新数还是3的倍数。

师：怎么证明这个发现是正确的？

生：再举例验证。

师：请同桌合作，一人举例，一人验证。

教师组织反馈交流，证明猜想是对的。

师：谁来说说自己的想法？

生：因为判断3的倍数的方法是算一算各个数位上的数字之和，交换了数字的位置，就像交换了算式中加数的位置，和不变。

生：我还发现了一个判断的窍门，如36，个位和十位上的数字都是3的倍数，那么就不用算了，它一定是3的倍数。

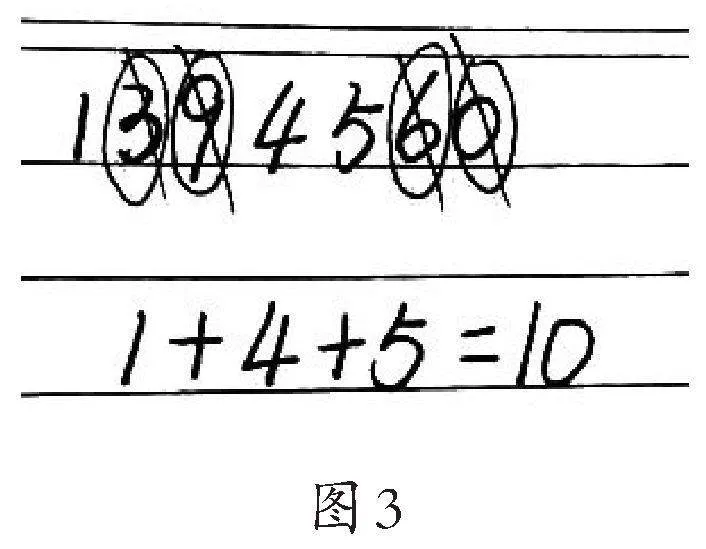
生：我同意，我们举的数比较大（如图3），我想3、9、6、0已经是3的倍数了，那我在算式中就不加了，直接加剩余的数，看看和是不是3的倍数就可以判断了。因为10不是3的倍数，所以1394560也不是3的倍数。

师：真为你们感到骄傲，一个看似简单的判断题，被大家这么一分析，原来还有那么多值得思考的问题。

教学片段二

师：下面请独立完成“练一练”第2题（如图4）。想一想，你有什么妙招吗？

生：题目要求在方框里填上一个数字，所以0～9这10个数字都有可能，从0开始逐个去试一试，和十位上的2加一加，如果是3的倍数就可以填。

师：有序试一试是个好方法，谁的方法和他的一样？试出的结果如何？

生：第1小题1、4、7都可以。

师：谁的方法和他们不一样？

生：我以第2小题为例，方框里有0～9这10种选择，最大的是9。9加上个位上的5等于14，而14以内的3的倍数有3、6、9、12。就用这四个数分别减去个位上的3，3不可以减5，6-5=1，9-5=4，12-5=7，因此可以填1、4、7。

生：也可以用上做第1小题的经验，就拿第3小题“□3”来说，个位上的3已经是3的倍数了，所以十位上只要填3的倍数就行，那就是3、6、9。

师：如果这个小题改成“3□”呢？

生：那还要多一个0。

师：仔细观察每一道题填写的所有情况，你有什么发现？

生：我发现每一道题的三个答案都是连续加3。

生：只要确定最小的一个答案，剩下的连续加3就行。

生：确定最大的，连续减3也行。

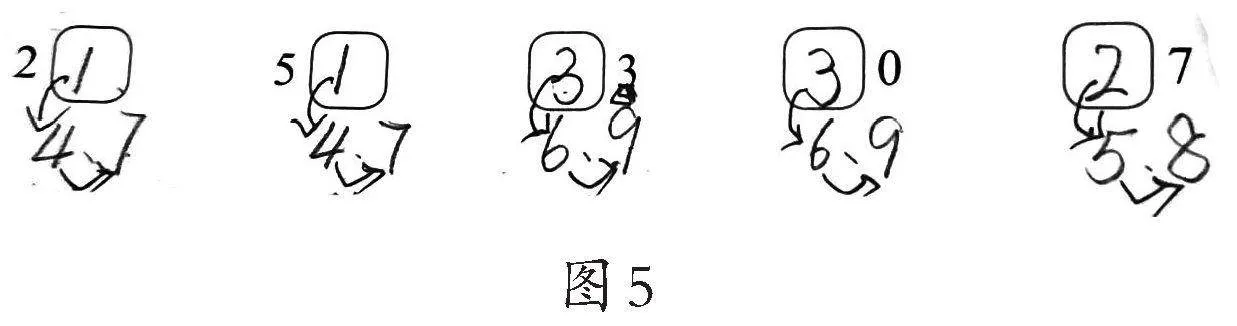
师：（出示学生作品，如图5）为什么呢？

生：个位上每次增加一个3，还是3的倍数。十位上每次增加一个3表示30，也是3的倍数。

师：完成题目的时候，多追问一下自己为什么，可以让自己更靠近知识的本质。

2022年版课标的主要变化之一是研制了学业质量标准，并在学业质量描述中指出：“学生经历数学的学习运用、实践探索活动的经验积累，逐步产生对数学的好奇心、求知欲，以及对数学学习的兴趣和自信心，初步养成独立思考、探究质疑、合作交流的学习习惯，初步形成自我反思的意识。”学业质量标准以核心素养为主要维度，因此，练习也是落实培养学生核心素养的重要途径。在练习中，我们同样要给予学生时间，鼓励他们驻足停留进行思考，让学生由“会”生“慧”，达成培育核心素养的目的。