大观念引领下的结构化课堂探索

在教学苏教版教材五年级上册“小数的意义”一课时，我们力图从结构化的角度进行思考，既关注本节课在“小数的意义和性质”单元中的地位和作用，还要站在理解整数、小数甚至分数计数单位表达的一致性上，让学生能整体建构数的认识和数的运算。

一、有效把握学生的认知起点

“小数的意义”是在学生认识自然数基础上一次数的扩充和延伸，也是学生后续学习小数的性质等知识的重要基础。在授课前，我们进行了如下的学情前测：

通过画一画、涂一涂、写一写的方式，利用图形或生活中的物品表示小数0.7。

从前测情况看，学生能用多种直观的形式表示0.7，能够初步认识一位小数就是十分之几。多样的呈现方式延续了三年级的学习内容，同时弥补了五年级教材中素材单一的问题（教材中只呈现了长度素材），为了放大图形在小数认识过程中的作用，充分发挥数与形的有效沟通，我们选择部分学生作品作为本节课的学习材料。

二、大观念引领下的单元整体分析

计数单位是本单元教学的关键所在。利用计数单位，可以整体建构知识间的联系，打通知识到核心素养的通道。“小数的意义”是本单元的核心内容，学生在感悟和理解小数意义的同时，既要建立小数和整数之间的联系，还要通过数与形的有效结合，对小数的组成、小数的大小比较、小数的性质等内容进行初步感悟。一节课辐射整个单元，为学生结构化的单元建构做好充分的准备。

三、单元学习目标和课时学习目标

（一）“小数的意义和性质”单元学习目标。

1.结合现实情境，理解小数的意义，会读、写小数，了解小数产生的价值。

2.在学习小数意义的过程中，充分感受计数单位的作用，沟通整数和小数之间的联系。在单元知识的学习中感悟小数数位的含义，建立位值概念。在理解和掌握小数的性质、小数的大小比较、小数的改写和小数的近似数等知识的过程中，感悟计数单位的重要性。

3.经历知识的形成过程，培养观察、比较、抽象、概括及合情推理的能力，渗透数形结合思想，发展数感。

4.经历解决问题的过程，体会小数与日常生活之间的密切联系，初步感悟结构化的学习方法，树立学好数学的信心。

（二）“小数的意义”课时学习目标。

1.在已有学习经验的基础上，依托数与形之间的紧密联系，通过分一分、数一数、涂一涂、比一比等活动，自主建构小数的意义及小数和整数之间的联系。

2.经历探索小数意义的过程，提升观察、分析和概括能力，进一步提升数感。

3.感受数学与生活之间的联系，激发学习数学的兴趣。

四、基于结构化的课堂教学实践

（一）回顾已有知识，初探结构关联（小数的产生）。

师：数[（sh ）][ù]的学习离不开数[（sh ）][ǔ]，用正方形表示1，1个1个地数，10个一就是1个十；10个10个地数，10个十是1个百……按照十进制一直数下去，会产生新的计数单位，帮助我们数出更大的数。如果从1开始分一分呢？

【设计意图】通过回顾，学生初步在心中建立两条“线”，一条为从1开始按照满十进一不断向左延伸的整数计数单位“线”，另一条为即将产生的从1开始向右延伸的小数计数单位“线”。

（二）多重角度关联，单元整体构建（小数的意义）。

1.从认识一位小数到认识两位小数。

（1）比较这几种方法（如图1），在表示0.7时有什么相同之处？（横向关联）

（2）我们选取的图（如图1所示的几种方式，此处略）不同，在表示0.73时有相同之处吗？（横向关联）

【设计意图】充分利用学生前测结果作为研究素材，通过横向对比丰富对一位小数的理解。在一位小数学习素材的基础上，学生通过猜想、尝试、比较等活动自主构建两位小数的意义。在这一过程中，素材的一致性更有利于学生对小数意义的整体建构。

2.小数也是数出来的（纵向关联）。

师：0.73里有几个0.01？想一想，0.73在计数器上怎么表示？从0.73开始继续数下去，你会数吗？

教师用课件演示拨珠过程，依次数出0.74、0.75、…、0.80。在此过程中交流：（1）0.77中的两个7表示的含义相同吗？（2）0.79里有几个0.01？（3）0.8既可以是80个0.01，也可以是8个0.1；（4）10个0.01就是1个0.1。

【设计意图】依托计数器和图形的直观演示，在数的过程中，学生直观认识和理解小数的组成，建立整数和小数计数单位之间的联系，初步感受小数的性质。这样的过程保持了认数方法的一致性，为单元知识的整体建构做好了铺垫和准备。

3.整体建构，深入理解内涵。

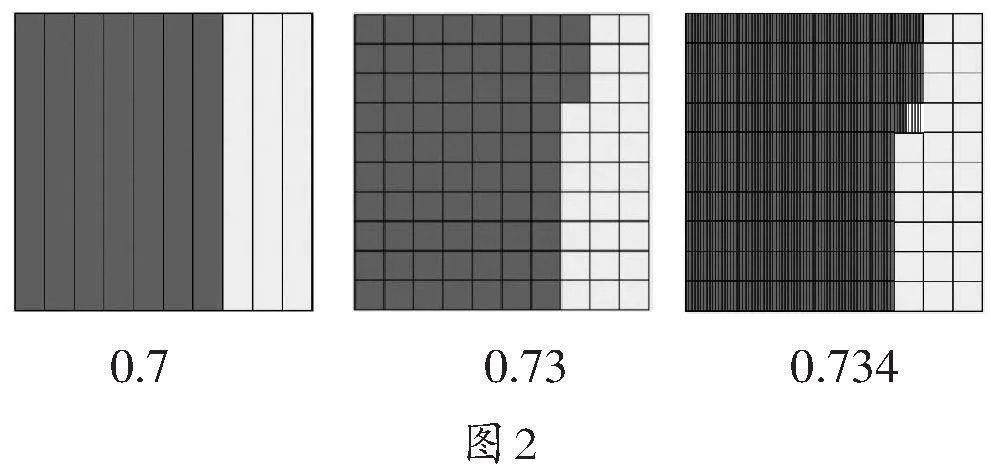
（1）小数的意义整体建构过程（如图2）。

（2）计数单位的整体建构过程（如图3）。

（3）利用数轴进行整数和小数的整体建构（略）。

【设计意图】为了体现数的认识的整体性和一致性，我们整节课把数和形进行有机整合，这样不仅有利于学生在已有知识的基础上自主建构小数的意义，也便于学生发现和概括出计数单位间的十进和“十分”关系，从而对整数和小数有整体性的认识。