自主规划单元学习，感悟运算的一致性

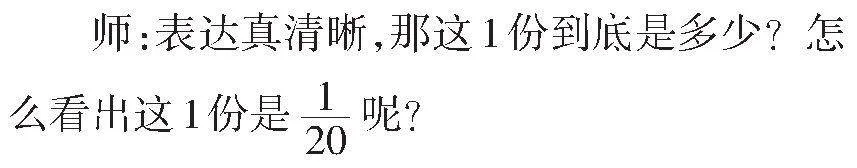
分数乘法与整数乘法、小数乘法运算之间有密切的联系，在运算意义、算理和算法上具有一致性，是学生对乘法意义理解的又一次丰富和扩充。正如2022年版课标指出的，小学阶段在感悟数的概念本质上的一致性的基础上，还要“感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识”。笔者团队整体构建了分数乘法单元，鼓励学生自主规划单元学习，以探索分数乘法通法为主线，引导学生首先想办法解决分数乘法如何计算，在此基础上沟通方法之间的联系，感悟运算的一致性。

下面重点介绍“分数乘分数”的教学过程及思考。本节课共有三个学习活动：一是规划研究素材，确定研究顺序；二是借助直观，探索分数单位×分数单位如何计算；三是由分数单位×分数单位的研究出发，研究更多分数乘法算式，如真分数×真分数、假分数×假分数等，明晰分数乘法的通法及其道理。

一、规划研究素材，确定研究顺序

上课伊始，通过播放本单元前面课时学习过程的小视频，帮助学生回顾学习过程中研究的问题、进行的思考和初步的研究成果，引领学生确定这节课的学习目标：寻找分数乘分数计算的通法。需要说明的是，通过前面的讨论，学生已经明确了什么是通法：能解决所有分数乘分数的计算问题，同时要简洁一些。

研究目标确定后，就研究素材问题，教师继续引导学生思考：选择哪些有代表性的算式进行研究呢？研究顺序是什么？在问题的引领下，学生独立思考、全班分享写的算式及背后的想法。

师：看来他俩在算式的处理上有点儿不同，第一位同学的方法和研究思路是一小步一小步地往前走，而第二位同学稍微调整了一下，但他俩的思考有共同之处——都想从简单的分子是1的分数开始研究，然后是真分数×真分数、假分数×假分数，大家同意吗？

此时不少学生并没有感觉到第一个算式实际上体现了分数单位的计算，只是觉得它简单，教师没有干预，而是顺应学生的想法。

生：（齐）同意。

【设计意图】通过前期研究过程的回顾，唤醒学生的学习经验，明确本节课的研究目标。对研究素材的规划，以及从分数单位入手由易到难研究顺序的确定，不仅发展了学生自主规划的能力，也为感悟计数单位的价值埋下了伏笔。

二、借助直观，研究分数单位的乘法

1.引导学生独立思考。

师：可以画一画、算一算或者写一写，说明你的想法。

学生独立研究，教师巡视并进行指导。

2.组织全班交流。

师：在交流的过程中，不仅要说清楚怎么计算，更要把计算方法背后的想法说明白。

在学生有了想法后，小组内交流，然后教师组织全班交流。

师：谁来说说自己的想法？

生2：我建议在第二次分的时候把竖着的线画通，这样可以直观地看出长方形被分成了几个格子，每个格子是几分之一（如图2）。

生3：先平均分成了4份，再把每份又平均分成了5份，所以一共平均分成了4×5=20（份）。

师：想一想，我们把刚刚两位同学分的过程用算式表达出来的话，应该怎么写呢？

生1：我们把整体“1”先平均分成4份，取其中的1份，然后又把那1份平均分成5份，取其中的1份。所以发现计算时只要用分母×分母就能算出来了。

教师结合学生的发现进行阶段性小结：两个分数单位相乘，结果还是分数单位，而且这个新的分数单位的分母是由原来两个分数单位的分母相乘得到的。

【设计意图】由分数单位的乘法入手进行研究，既顺应学生自主研究的探索路径，又为突破探索分数乘分数的计算方法提供了研究支架。

三、探索更多的乘法算式，明晰通法及其道理

学生在独立思考的基础上，围绕以下三个问题，在小组内进行初步的交流：

（1）想计算哪个算式？你怎么想到要计算它呢？

（2）在介绍算式时，不仅要说你是怎么算的，关键是要说出你背后的想法及为什么这么算。

经过同伴的互相启发，全班分享想法。

1.真分数×真分数。

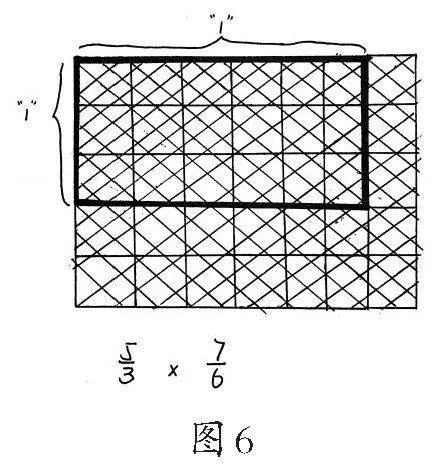
组2：我们借助单位来说明（如图4）。

师：你们计算的每一步的依据是什么？

学生在独立思考、小组内分享的基础上，进行全班交流。

师：谁来说说自己的想法？

学生虽然主动从单位的角度进行了探索，但对感觉“画不出来的图”仍然想要研究，于是教师聚焦“卡点”，鼓励学生进一步思考。

师：想一想，画不出来的关键“卡”在哪儿了？

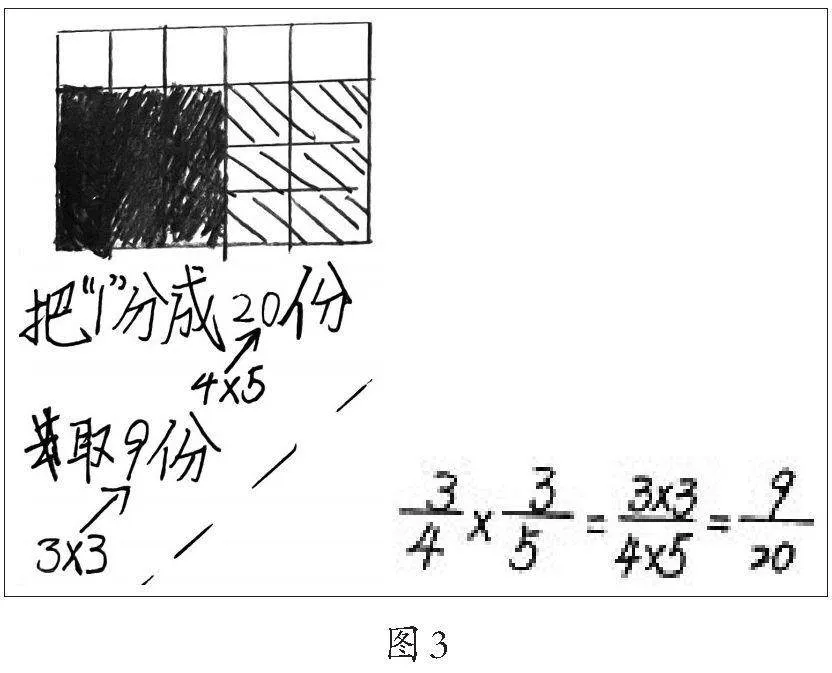
生2：假分数怎么在图中表示呢？

此时，教师带领学生完整回忆整个研究的过程，并引发对通法背后道理的思考。

师：回头看一下，你们的“胆子”越来越大了，由刚开始想到要解决分母没发生变化的真分数×真分数，到最后研究貌似“完全不搭边”的假分数×假分数。在这一连串的算式计算过程中，你觉得虽然算式不同，但相同的地方是什么？谁帮我们找单位呢？个数又怎么找呢？

生：在计算时，都在思考新的分数单位是什么，有几个这样的分数单位。我发现分母×分母算的就是产生的新分数单位的分母是多少，分子×分子则算出了有几个这样的分数单位。

大家鼓掌表示赞同。

【设计意图】由分数单位的乘法出发展开联想活动，从开始学生想到要解决分母没发生变化的真分数×真分数的问题，直至解决假分数×假分数的问题。在这一连串的问题解决过程中，学生自主发现“理”的一致性。

本节课中，在核心问题“分数乘分数计算的通法是什么”的驱动下，鼓励学生自主思考，在对“法”的理解和寻找的过程中，从分数单位×分数单位，到真分数×真分数、假分数×假分数，学生逐步发现通法及其背后的道理，感悟分数单位的价值，为进一步寻求乘法运算的一致性奠定了良好的基础。